基于GARCH-分形布朗运动模型的碳期权定价研究
2016-01-29刘宇佳
张 晨, 彭 婷, 刘宇佳
(合肥工业大学 管理学院,安徽 合肥 230009)
基于GARCH-分形布朗运动模型的碳期权定价研究
张晨,彭婷,刘宇佳
(合肥工业大学 管理学院,安徽 合肥230009)
摘要:文章将广义自回归条件异方差(generalized autoregressive conditional heteroskedasticity,GARCH)模型和分形布朗运动结合引入碳金融期权定价研究中。通过对欧洲碳排放配额(European Union Allowance,EUA)期货收盘价的样本数据检验,发现其存在尖峰厚尾、条件异方差性和分形特征;采用GARCH模型拟合并预测碳价收益率波动率;将预测的波动率作为输入值代入分形布朗运动期权定价方法,运用蒙特卡罗模拟对EUA期货期权进行定价,并与B-S期权定价法(Black-Scholes Option Pricing Model)比较。结果表明,基于GARCH分形布朗运动模型的碳期权定价法预测精度有显著提高。
关键词:碳期权定价;广义自回归条件异方差模型;分形布朗运动;B-S期权定价
近年来碳排放权的交易受到越来越多的关注,也成为理论界研究的重点。2005年正式生效的《京都议定书》确立了联合减排(joint implementation,JI)、国际排放权交易(international emissions trading,IET)和清洁发展(Clean Development Mechanism,CDM)3种国际碳减排机制[1]。碳排放权市场化最核心的问题是要解决碳金融资产定价。国际碳排放交易体系经过长期的发展,已经形成了较为成熟的现货价格形成机制,但目前缺乏对碳衍生品价格形成机制的研究,尤其是碳期权定价方面的研究,而碳期权作为碳排放市场中的一种重要交易产品,在提高碳排放市场的价格发现功能和规避碳排放市场风险等方面具有重要作用。因此,研究碳期权的定价问题,通过了解其价格特征,掌握其内在规律,有助于投资者做出较为合理的碳期权套期保值决策,以便降低碳交易风险。
我国为全世界核证减排量一级市场上最大供应国。尽管我国已在北京、上海、天津、重庆、湖北、广东和深圳等7省市建立了区域性碳排放交易所,但目前仍处于起步阶段,且交易产品主要以现货交易为主,碳期权交易平台有待开通。由于基础数据的缺乏,目前我国对实现碳期权科学合理定价的研究较少。本文探讨国际碳排放交易体系中碳期权的定价方法,为我国未来碳期权交易的科学定价提供借鉴。
1国内外研究现状
1.1 传统金融期权定价的研究
金融期权定价的重点在于对原生资产价格变化的准确刻画。1970年以来产生了Black-Scholes(B-S)期权定价法、Hull-White期权定价法、二叉树期权定价法、分形布朗运动期权定价法等期权定价方法,其中B-S期权定价法和分形布朗运动期权定价法是学术界比较常用且易于操作的方法。
B-S期权定价法是在文献[2]提出的期权定价模型基础上,假定标的资产价格相互独立且服从几何布朗运动,以及标的资产收益率独立同分布且服从正态分布下提出来的[3]。但近年来,学者们对资本市场的大量研究表明金融资产价格并非遵循几何布朗运动,即金融资产的收益率并非服从正态分布,而是服从一种尖峰厚尾的分布;且金融资产价格之间也不是独立的,而是存在着长期相关性[4-7]。因此,B-S期权定价法在现实运用中存在一定的局限性。
而分形布朗运动期权定价法是文献[8]在文献[9]提出分形布朗运动的基础上,首次将其应用于金融期权定价而产生的。分形布朗运动与几何布朗运动最主要的区别是分形布朗运动中的增量是不独立的,而几何布朗运动中的增量是独立的。由于分形布朗运动期权定价法能够很好地刻画标的资产价格的自相似性、厚尾性、长记忆性,且不要求标的资产价格相互独立、服从几何布朗运动以及标的资产收益率服从正态分布,因而更符合金融期权价格的实际特征。随后很多研究者在假定股价波动率为常量的情况下,运用分形布朗运动期权定价法研究股票期权市场的定价问题,验证了分形布朗运动期权定价法优于B-S等期权定价法[10-13]。
1.2 碳期权定价的研究
碳期权作为一种新型的金融期权产品,具有不同于传统金融期权的风险和市场特征。在碳期权定价时考虑碳市场的风险和市场特征,更能准确反映碳期权的真实价值。
有关碳期权定价的研究,除了文献[14] 建立随机游走模型对欧盟排放交易体系下Powernext和Nord Pool 2个排放交易市场的现货、期货和期权进行定价外,其他研究者几乎都选用B-S期权定价法对碳期权进行模拟定价,且定价时选用历史波动率作为B-S期权定价法的输入变量[15]。
有关碳金融资产价格波动率刻画的研究,国内外主要围绕欧盟之间交易的碳金融产品。文献[16-18]的研究发现:不论是二氧化碳排放交易市场还是二氧化硫排放交易市场,不论是欧洲的国家还是美国,碳金融资产价格波动率不是恒定的常量,而是具有鞅属性和时间-价格依赖性的波动结构,即波动率具有时变性。文献[19]发现碳价是一个有偏的随机游走分布,即对数收益率拒绝服从正态分布,且碳价具有尖峰厚尾以及长记忆性的特征。研究者在刻画碳资产价格波动率时,都赞同采用广义自回归条件异方差(generalized autoregressive conditional heteroskedasticity,GARCH)模型来刻画时变波动率,但具体选用何种GARCH模型需要根据研究对象的特征而确定[20-21]。
由于碳市场波动率表现出的时变性与历史波动率并不相符,且碳价收益率也不服从正态分布,因此,在定价时考虑碳价的分形特征和碳价波动率的时变特征更符合碳市场的真实情况。为提高碳期权定价的精确度,本文将GARCH和分形布朗运动结合引入碳期权定价研究,建立基于GARCH-分形布朗运动模型的碳期权定价方法新思路:首先采用GARCH预测碳资产价格的波动率,将预测的波动率作为输入值代入分形布朗运动,预测碳资产价格序列;然后运用风险中性条件下的期权定价法对碳期权进行蒙特卡罗模拟定价,并将模拟结果与B-S期权定价结果进行比较,检验本文的碳期权定价方法的有效性。
2研究设计
2.1 碳价收益率波动率的预测方法
GARCH模型是由Bollerslev在自回归条件异方差(autoregressive conditional heteroskedasticity,ARCH)模型的基础上改进得到的[22],自产生至今在金融领域有广泛的应用。 如果随机变量yt可以表示为(1)式,则称ut服从q阶ARCH过程。
yt=α0+α1xt-1+α2xt-2+…+αmxt-m+ut
(1)
(2)
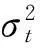
在(2)式条件方差中加入残差平方的滞后项即构成GARCH模型,如(3)式所示:
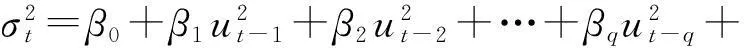
(3)
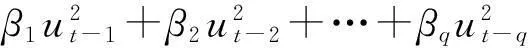
β0>0;β1,…,βq≥0;x1,…,xp≥0;
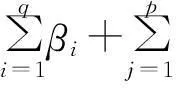
实证研究表明GARCH 模型能够较好地描述碳金融资产收益波动率的异方差现象和波动聚集现象[20-21]。本文利用GARCH模型对碳金融资产收益波动率进行预测,预测结果作为分形布朗运动模型输入值,可对碳期权进行定价。
2.2 碳金融资产分形布朗运动期权定价方法
由于碳资产价格收益序列存在尖峰厚尾、自相关性等特征[19],因此,本文使用文献[8]提出的分形布朗运动期权定价法中的资产价格变动过程来刻画碳资产价格随机序列:
dS(t)=μ(t)S(t)dt+σ(t)S(t)dBH(t)
(4)
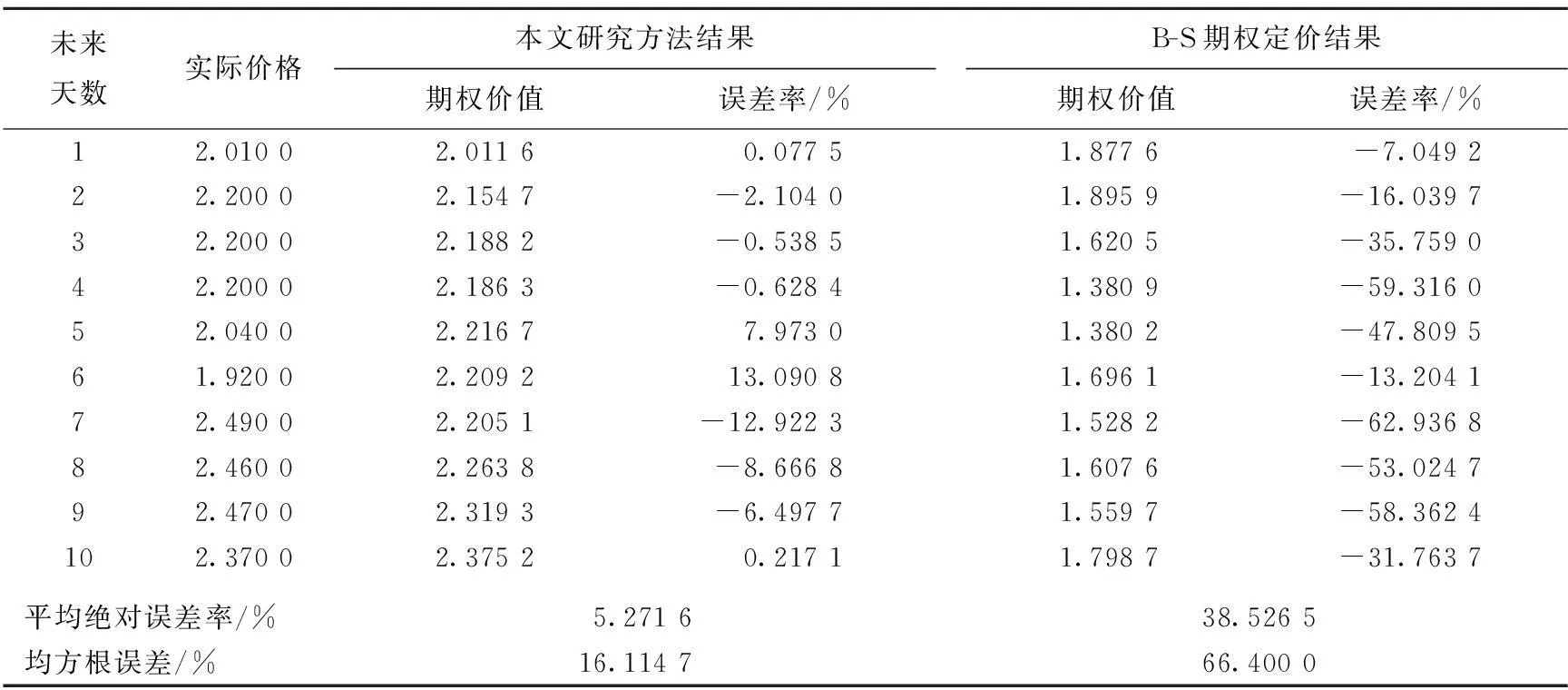
其中,S(t)为碳资产价格随机序列,0≤t≤T;μ(t)为碳资产期望收益率;σ(t)为碳资产收益率年化瞬时波动率;BH(t)为具有H指数的分形布朗运动,其中0 分形布朗运动的模拟主要有精确方法和逼近方法,精确方法是通过一系列的数学推导,求导出分形布朗运动的具体表达式,主要有Hosking方法、Cholesky方法、Davies和Harte方法;而逼近方法不要求直接求解分形布朗运动的具体表达式,而是采用无限分割逐渐接近的方法求解分形布朗运动的增量,主要有随机中点位移法和谱分析方法等[23]。结合本文(4)式刻画碳资产价格变动过程涉及分形布朗运动增量的描述,本文采用随机中点位移法中由文献[24]提出的扩展Maruyama法模拟分形布朗运动增量,公式为: dBH(t)=ω(t)(dt)H (5) 其中,0 分形布朗运动期权定价方法是基于分形布朗运动刻画碳资产价格随机序列,采用风险中性假设进行期权定价的一种方法。本文采用文献[25]在风险中性条件下用无风险收益率折现期望收益得到的欧式看涨期权理论价值,具体公式如下: C(t)=e-r(T-t)E[max(ST-X),0] (6) 其中,随机变量ST为碳价到期日现货价格;r为无风险利率;T-t为期权剩余有效期限;X为碳期权合约的执行价格。 本文在选取碳期权标的碳价样本的基础上,计算出标的碳价日收益率序列;在对碳价日收益率序列进行描述性统计、平稳性检验、自相关和偏自相关检验、ARCH检验以及Hurst检验之后,结合碳价日收益率序列的特征构建GARCH模型,并估计GARCH模型的参数,运用GARCH模型对标的碳价日收益率波动率进行预测;最后将GARCH模型预测的波动率作为分形布朗运动期权定价方法中的输入值,从而实现对碳期权的定价。 为更好地衡量基于GARCH分形布朗运动模型的碳期权定价方法的效果,本文同时计算了基于历史波动率的B-S碳期权定价方法的定价结果,并将2种碳期权定价结果分别与实际碳期权交易价格收盘价比较,进而验证本文提出的碳期权定价方法的有效性。 3实证分析 考虑数据的可获得性和完整性,本文选取洲际交易所(https://www.theice.com)2013-04-09—2014-04-17期间的2014年12月到期的EUA期货每日收盘价为样本内研究对象,同时剔除在此期间无成交量导致收盘价为零的交易日数据,为使检验效果更好,本文选取的碳价对数收益率为R=100(lnPt-lnPt-1),总计获得有效数据为264个。本文以该期间的交易数据进行数据样本检验,估计出GARCH模型参数和预测未来10 d的日波动率,同时以此期间的碳价收益率序列计算碳价收益率的日历史波动率。 为验证碳期权定价方法的合理性,本文选取伦敦洲际交易所中以2014年12月到期的EUA期货为标的、2014-04-18—2014-05-01期间的EUA期货期权每日交易收盘价为验证对象。 碳价收益率序列描述性统计见表1所列,碳价收益率序列的峰度值为22.037 27,显著大于正态分布的峰度值3;偏度值为-2.355 335,显著异于正态分布的偏度值0;该序列的Jarque-Bera统计量为4 230.688,P值显著接近于0。这说明碳价收益率序列存在“尖峰厚尾”现象,显著不服从正态分布。 表1 碳价收益率序列描述性统计 对碳价收益率做平稳性检验发现,碳价收益率序列的ADF平稳性检验统计量值为-14.577 62,小于在1%显著性水平下的临界值-3.455 193,同时分别小于在显著性水平5%和10%下的临界值-2.872 370和-2.572 615,可得出碳价收益率序列为平稳时间序列。 在平稳性检验的基础上,进一步检验碳价收益率的自相关性和偏自相关性。分别计算碳价收益率时间序列残差和残差平方的36阶滞后项相关系数和偏自相关系数,发现其均存在自相关和偏自相关,并结合AIC(Akaike information criterion)最小原则,AR(2)具有最优的拟合结果。 为进一步检验碳价收益率序列是否存在ARCH效应,本文对用AR(2)拟合后的残差序列进行ARCH-LM检验,结果表明P值均为0,拒绝序列不存在ARCH效应的原假设;残差序列的ARCH效应很明显,即AR(2)模型的残差存在自回归条件异方差。 为验证碳价收益率是否存在分形特征,本文采用R/S类方法计算的Hurst指数来判断。本文计算出2013-04-09—2014-04-17期间碳价收益率的Hurst指数值为0.676 5,该值大于0.5,说明碳价收益率具有长记忆性,即存在分形特征。 鉴于上述样本数据检验中碳价收益率是平稳序列以及存在ARCH效应的检验结果,碳价收益率时间序列符合GARCH模型的构建条件。本文建立AR(2)-GARCH(1,1)-N模型来刻画碳价收益率的波动率,模型参数估计具体公式如下: rt=0.253 036+0.168 054rt-1- 0.184 222rt-2+εt (7) (8) 参数估计模型中,β0=0.963 283>0,β1=0.746 207>0,χ1=0.140 120>0,且满足GARCH模型构建的约束条件,即 β1+χ1=0.746 207+0.140 120= 0.886 327<1。 对通过AR(2)-GARCH(1,1)-N模型模拟后的残差和残差平方进行自相关和偏自相关检验,发现其已经不存在自相关和偏自相关。本文同时对模拟后的残差进行ARCH检验,发现用AR(2)-GARCH(1,1)-N模拟后的残差序列的ARCH检验结果中P值为17.10%,说明模拟后的残差序列不存在ARCH效应。 综上所述,经过GARCH(1,1)-N模型的处理,碳价收益率序列的各种信息得到了很好的描述。因此,本文构建的GARCH模型对碳价收益率波动率的刻画是合理的。 本文根据已估计的AR(2)-GARCH(1,1)-N模型,以2014-04-17为基准日,向前预测R的未来10 d碳价收益率日波动率,随后计算R/100的未来10 d日波动率,具体的计算数据见表2所列。由于分形布朗运动价格变动过程公式中所采用的波动率是年化波动率,因此,本文根据(9)式将未来10 d日波动率转化为年化波动率。 (9) 表2 预测的碳价收益率波动率未来10 d数据 本文以EUA期货欧式看涨期权为定价对象,选取碳期权合约中交易较为活跃、价格较大的碳期权作为计算对象。 该期权标的为2014年12月到期的EUA 期货,其执行价格为3.5欧元/吨二氧化碳当量。随后分别采用本文提出的碳期权定价方法和B-S期权定价法对EUA期货期权运用蒙特卡罗模拟进行模拟定价,然后将2个定价的结果分别和实际EUA期货期权交易价格进行比较分析。其中运用B-S期权定价法定价时,采用(10)式计算2013-04-09—2014-04-17期间碳价收益率的日历史波动率,并结合年化波动率计算公式,得出此期间的年化历史波动率为0.669 1。 (10) 本文运用Matlab对2种期权定价方法分别用蒙特卡罗模拟10 000次,模拟结果见表3所列。 表3 碳期权模拟定价结果比较 由表3可知,本文提出的碳期权定价方法的模拟结果与碳期权实际交易价格的误差率最大仅为13.090 8 %,最小为0.077 5%;而基于B-S的碳期权定价结果中最大的绝对误差率为62.936 8%,最小的也有7.049 2%。并且采用平均绝对误差率和均方根误差2个统计量来衡量2个期权定价模型的精确程度时,本文提出的碳期权定价方法的模拟结果的平均绝对误差率和均方根误差分别为5.271 6 %、16.114 7 %,均小于B-S期权定价结果的38.526 5%和66.400 0%。结果表明本文提出的碳期权定价方法的模拟定价结果显著优于B-S期权定价方法的定价结果。 本文提出的碳期权定价方法比B-S的碳期权定价方法有效的主要原因在于: (1) 从实际的数据检验中发现,碳价收益率的残差平方是存在波动聚集效应的,且ARCH效应检验表明碳价收益率波动率存在条件异方差,说明碳价收益率波动率不为恒定常量。本文提出的碳期权定价方法在定价时考虑的波动率是时变的,而B-S期权定价法假定波动率是一个恒定常量。因此,碳价收益率波动率不为恒定常量这一现象不符合B-S期权定价方法假定,使得B-S期权定价方法模拟结果较大偏离实际碳期权价格。 (2) 碳价的Hurst指数检验值为0.676 5,并不等于0.5,说明碳价并不遵循几何布朗运动。本文提出的碳期权定价方法认为碳价的变化过程符合分形布朗运动,而B-S期权定价法认为碳价的变化过程符合几何布朗运动,故而碳价不遵循几何布朗运动的这一结论不符合B-S期权定价方法的假定,使得B-S期权定价方法的模拟结果偏离实际碳期权价格。 因此,本文提出的碳期权定价方法更符合现实情况,比B-S期权定价方法更优。 为检验本文提出的碳期权定价方法的稳健性,本文改变以2014年到期的EUA期货为标的的期权合约执行价格,选取交易较为活跃的执行价格为每吨二氧化碳当量4.5欧元的碳期权合约作为验证对象,验证结果发现:本文提出的碳期权定价方法的模拟定价结果的误差率绝对值仍然全部低于B-S期权定价方法的模拟定价结果。因此,本文提出的研究方法具有很好的稳健性。 4结束语 本文提出了基于GARCH分形布朗运动模型的碳期权定价方法,实证结果发现: EUA期货价格收益率呈现出尖峰厚尾、条件异方差以及分形现象;AR(2)-GARCH(1,1)模型能很好地刻画碳价收益率的时变波动率; 基于GARCH分形布朗运动模型的碳期权定价方法的预测精度显著高于B-S期权定价方法的预测精度。 本文的研究贡献在于将分形布朗运动和GARCH模型结合,提出一种贴合碳金融市场特征的欧式碳期权定价方法,有助于投资者做出较为合理的碳期权投资决策,以便降低碳交易风险;同时为我国未来开展碳期权交易、实现科学定价提供借鉴。由于本文提出的碳期权定价方法在10 d以内的效果比较稳健,而10 d以外的效果稳健性较差,因此,本文提出的基于GARCH分形布朗运动模型的碳期权定价方法适用于碳期权的短期价格预测,而有待进一步考虑使用诸如随机波动率模型与分形布朗运动的结合,来预测碳期权较长期价格。 [参考文献] [1]Barrett S. Political economy of the Kyoto Protocol[J].Oxford Review of Economic Policy,1998,14(4):20-39. [2]Bachelier L.Theorie de la speculation[J].Annales Scientifiques de I’E′cole Normale Supérieure,1900,3(3):21-86. [3]Black F, Scholes M. The pricing of options and corporate liabilities [J]. Journal of Political Economy,1973, 81(3):637-654. [4]赵旭.基于分形B-S定价模型的认购权证价格行为实证分析[J].数理统计与管理, 2008.27(6):1039-1046. [5]Necula C.Option pricing in a fractional Brownian motion environment,Mathematical Reports 02/2002[R].2002.doi:10.2139/ssrn.1286833. [6]张卫国,肖炜麟,徐维军,等.分数布朗运动下欧式汇率期权的定价[J].系统工程理论与实践,2009,29(6):68-29. [7]卢树强,包树新.分数布朗运动环境下一类新型期权定价的鞅分析[J].合肥工业大学学报:自然科学版, 2013, 36(7): 875-878. [8]Hu Y, ∅ksendal B. Fractional white noise calculus and applications to finance[J]. Infinite Dimensional Analysis, Quantum Probability and Related Topics,2003,6(1):1-32. [9]Mandelbrot B,van Ness J.Fractional Brownian motions, fractional noises and applications [J].SIAM Rev,1968,10(4):422-437. [10]梅正阳,祁改珂,王同柱.Hurst指数属于(1/3, 1/2)的分数模型的期权定价[J].应用数学,2011,24(3):617-623. [11]黄煜可.几何分数布朗运动下期权定价的时间轴变换法[J].统计与决策,2009(5):10-12. [12]孙琳.分数布朗运动下带交易费用的期权定价[J].系统工程,2009(9):36-40. [13]周银,杜雪樵.分数布朗运动下的亚式期权定价[J].合肥工业大学学报:自然科学版,2011, 34(2):317-320. [14]Daskalakis G,Psychoyios D,Markellos R N. Modeling CO2emission allowance prices and derivatives: evidence from the European trading scheme[J].Journal of Banking & Finance,2009,33(7):1230—1241. [15]王锐.碳排放权交易的市场定价[D].哈尔滨:哈尔滨工业大学,2010. [16]Seifert J, Uhrig-Homburg M, Wagner M. Dynamic behavior of CO2spot prices[J]. Journal of Environmental Economics and Management,2008, 56(2):180-194. [17]Paolella M S, Taschini L. An econometric analysis of emission allowance prices[J].Journal of Banking & Finance,2008,32(10): 2022-2032. [18]Benz E,Trück S. Modeling the price dynamics of CO2emission allowances[J].Energy Economics,2009,31(1):4-15. [19]Chevallier J. Carbon futures and macroeconomic risk factors: a view from the EU ETS[J].Energy Economics,2009,31(4): 614-625. [20]陈晓红,王陟昀.欧洲碳排放权交易价格机制的实证研究[J].科技进步与对策,2010,27(19):142-146. [21]Feng Zhehua,Zou Lele, Wei Yiming. Carbon price volatility: evidence from EU ETS[J].Applied Energy,2011,88(3):590-598. [22]Bollerslev T. Generalized autoregressive conditional heteroscedasticity[J]. Journal of Econometrics, 1986, 31(3):307-327. [23]Dieker T. Simulation of fractional Brownian motion[D].Enschede,The Netherlands: University of Twente,2002. [24]Jumarie G.On the representation of fractional Brownian motion as an integral with respect to (dt)a[J]. Applied Mathematics Letters, 2005,6(18): 739-748. [25]Cox J,Ross S. The valuation of options for alternation stochasic processes [J].Journal of Financial Economics,1976,3(3):145-166. (责任编辑张淑艳) Carbon option pricing based on fractional Brownian motion combined with GARCH model ZHANG Chen,PENG Ting,LIU Yu-jia (School of Management, Hefei University of Technology, Hefei 230009, China) Abstract:This paper introduces the idea of combining generalized autoregressive conditional heteroskedasticity(GARCH) model and fractional Brownian motion into carbon option pricing. Firstly, the test results from closing price of European Union Allowance(EUA) Futures show that obvious peak and fat tails, heteroscedasticity and fractal feature reside in the data. Secondly, the GARCH model is used to fit the volatility of EUA Futures price, which can reasonably describe and forecast the time-varying volatility. With the forecasted volatility being the input in fractional Brownian motion carbon option pricing, the Monte Carlo simulation is used to simulate the pricing of EUA Futures options, and then the pricing result is compared with that of Black-Scholes option pricing model. The result shows that carbon option pricing based on fractional Brownian motion combined with GARCH model can improve the pricing accuracy. Key words:carbon option pricing; generalized autoregressive conditional heteroskedasticity(GARCH) model; fractional Brownian motion; Black-Scholes option pricing doi:10.3969/j.issn.1003-5060.2015.11.022 作者简介:徐晟(1972-),男,湖北浠水人,博士,合肥工业大学副教授,硕士生导师. 基金项目:教育部人文社会科学研究基金资助项目(11YJA630167);安徽省软科学研究计划资助项目(1402052017) 收稿日期:2014-10-23;修回日期:2015-04-10 中图分类号:F831.5 文献标识码:A 文章编号:1003-5060(2015)11-1553-062.3 GARCH模型分形布朗运动碳期权定价
3.1 样本选取及预处理
3.2 碳价收益率特征检验
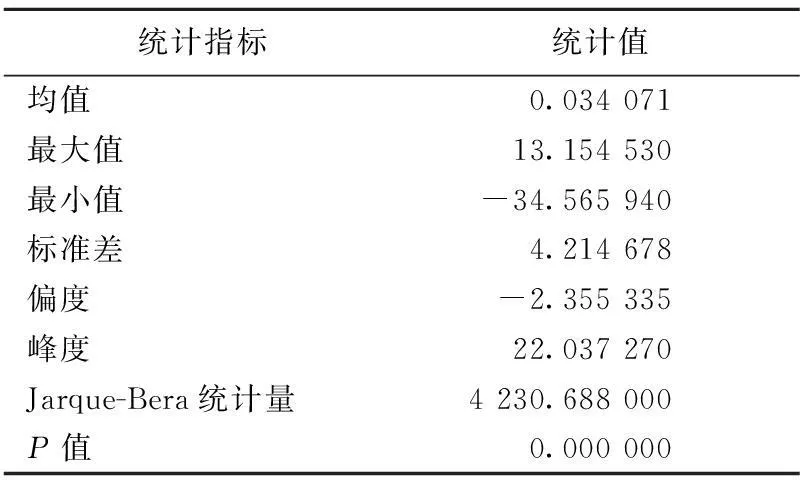
3.3 GARCH模型的参数估计和验证
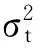
3.4 碳价收益率波动率的预测

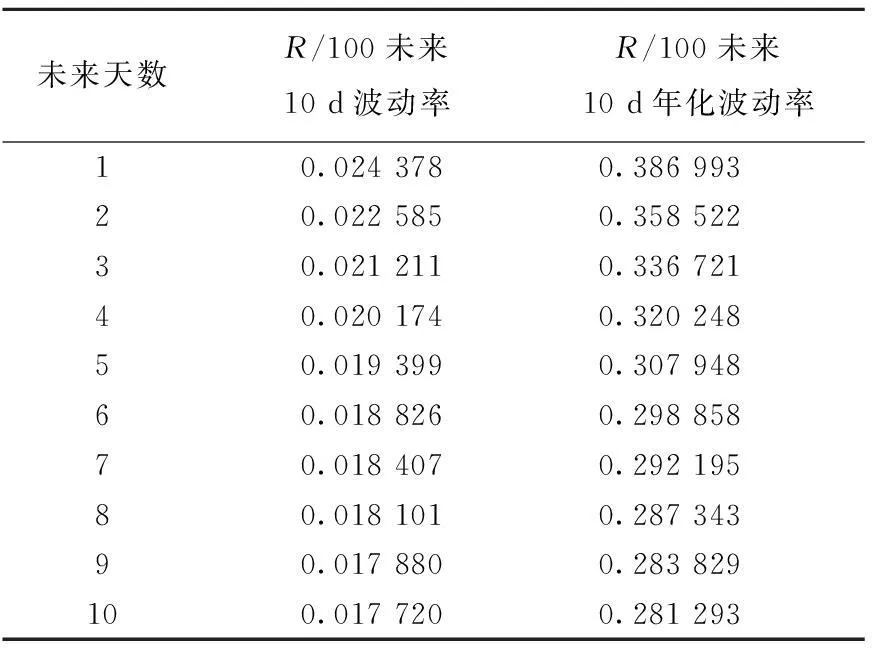
3.5 实证结果及其分析