汽油机瞬态空燃比的混沌时序LS-SVM预测研究

徐东辉,　代冀阳

(1.宜春学院 物理科学与工程技术学院,江西 宜春　336000; 2.长沙理工大学 工程车辆轻量化与可靠性技术湖南省高校重点实验室,湖南 长沙　410076； 3.南昌航空大学 信息工程学院，江西 南昌　330063)



汽油机瞬态空燃比的混沌时序LS-SVM预测研究

徐东辉1,2,代冀阳3

(1.宜春学院 物理科学与工程技术学院,江西 宜春336000; 2.长沙理工大学 工程车辆轻量化与可靠性技术湖南省高校重点实验室,湖南 长沙410076； 3.南昌航空大学 信息工程学院，江西 南昌330063)

摘要:在汽油机瞬态空燃比反馈控制过程中,氧传感器存在传输时滞,不能快速反馈汽油机瞬态空燃比真实值,无法满足瞬态空燃比反馈控制的实时性要求。文章提出了汽油机瞬态空燃比的混沌时序LS-SVM(最小二乘支持向量机)预测模型,采用相空间重构技术对原始数据进行重构,达到恢复汽油机瞬态空燃比时间序列的多维空间非线性特性目的,最后利用LS-SVM 进行训练及预测,得到空燃比预测结果。仿真结果表明,与Elman网络及前馈BP网络相比,混沌时序LS-SVM预测模型具有更强的非线性预测能力,能够有效地提高瞬态空燃比的预测精度,为瞬态空燃比反馈控制的成功实行提供了有力的依据。

关键词:瞬态工况;空燃比;LS-SVM预测模型;相空间重构;预测

目前,国内外对瞬态空燃比的控制主要采用氧传感器构成的反馈控制策略,但氧传感器存在反馈延迟,且反馈信息仅是发动机系统燃烧后的数据,无法对燃烧之前的系统偏差进行及时有效的修正,因此由氧传感器构成的发动机空燃比反馈控制方法无法提高瞬态空燃比控制精度及实时性[1-5]。研究人员提出了采用人工智能的预测方法。文献[6]利用Elman神经网络对过渡工况空燃比进行辨识;文献[7]在汽油HCCI发动机的空燃比控制方法上,采用了神经网络预测模型对空燃比进行预测,目的是提高空燃比反馈控制方法的控制精度及实时性;文献[8]采用BP神经网络对瞬态工况空燃比进行有效辨识。但是,神经网络遵循经验风险最小化准则,存在过拟合、泛化能力低、收敛速度慢等易陷入局部极小值的缺点,使得发动机空燃比控制系统的控制精度及实时性也受到限制;LS-SVM(最小二乘支持向量机)遵循结构风险最小化原则,可以克服神经网络存在的上述缺陷[9]。空燃比基于汽油与空气构成的混合体,其时间序列存在混沌性,利用重构技术恢复空燃比原有的混沌性,将有利于提高空燃比预测精度。

本文将混沌时序与LS-SVM两者有效地融合起来,建立一种混沌时序LS-SVM预测模型,提高汽油机瞬态空燃比的预测精度。仿真结果表明,与Elman网络及前馈BP网络相比,混沌时序LS-SVM预测模型具有更高的预测精度、更强的非线性预测能力及较好的应用价值,为空燃比反馈控制提供了一种较好的策略。

1空燃比混沌时序的判定

文献[10-11]提出了相空间重构理论,即在拓扑意义下,可以从一维时间序列中构造一个与原系统等价的相空间结构,较好地实现原系统的性质与规律。相空间重构的原理如下:设汽油机空燃比的时间序列为{λ(ti),i=1,2,3,…,n},选取一个合适的延滞时间τ构成m维向量,即

λ′(ti)={λ(ti),λ(ti+τ),λ(ti+2τ),…,

λ[ti+(m-1)τ]},i=1,2,3,…,n

(1)

其中,τ=kΔt为延滞时间,k为整数,Δt为采样间隔;m为嵌入维数,M=N-(m-1)τ为相点数。经研究显示,当τ、m选择恰当时,重构后的相空间与原系统具有相同的拓扑性质。

1.1　最佳嵌入维数m及延迟时间τ的求取

利用C-C方法[12]计算m和τ,可得:

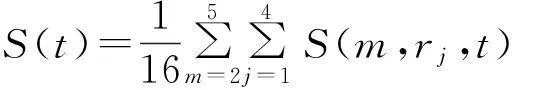
(2)

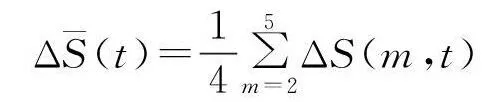
(3)

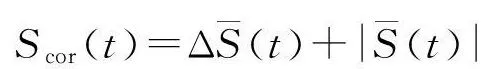
(4)

其中，S(t)为所有时间序列中子序列的统计量；ΔS(m,t)为所有时间序列的差量；rj为领域半径。

从(3)式中的第1个极小值寻找时间序列独立的第1个局部最大值,时间延迟τ=tτs对应着第1个局部最大时间[12-13]。同样,从(4)式中的最小值寻找时间序列独立的第1个整体最大值时间窗口,τw=tτs(τs为时间序列的采样间隔)对应着第1个局部最大时间,计算可得τ=2,τw=14,所以时间延迟为2d,由τw=(m-1)τ可计算出相空间重构的嵌入维数m=8。

1.2　空燃比时间序列的混沌识别

判断空燃比时间序列混沌特性的步骤[13]如下。

(1) 用快速傅立叶变换求取汽油机空燃比时间序列{λ(ti),i=1,2,3,…,n}的平均周期;经计算,汽油机空燃比时间序列的平均频率为0.048,平均频率的倒数为平均周期,值为20.8。

(2) 利用C-C方法确定最佳嵌入维数m及延迟时间τ,根据计算得出m=8和τ=2。

(3) 采用相空间重构技术对空燃比时间序列{λ(ti),i=1,2,3,…,n}进行重构。

(4) 假设Di(0)为第i个点到其最近邻域的距离,其表达式为:

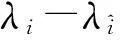
(5)

其中,ω=T/Δt,Δt为序列的采样周期。

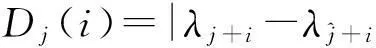
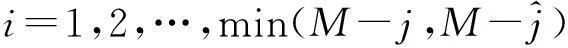
(6)

(6) 求解最大Lyapunov指数γi。在相空间中,若第i个最近邻点近似于以最大Lyapunov指数的速率发散,即di(j)=Ciexp(γijΔt)

(7)

其中,Ci为初始的分离距离常数;对(7)式两边取对数,可得:

lnDi(j)=lnCi+γi(jΔt),i=1,2,…,n

(8)

(8)式可以近似表示为一簇斜率为γi的平行线,采用最小二乘法对其进行拟合,得出最大的Lyapunov指数,即

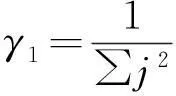
(9)

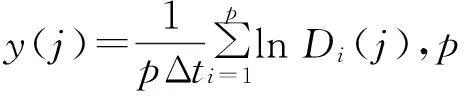
通过上述步骤和方法求得τ=2、m=8,根据(9)式计算出最大的γ1=0.005 7>0,表明瞬态空燃比时间序列具有混沌性,故可对它做短期预测。

2混沌时序LS-SVM预测模型建立

2.1　最小二乘支持向量机(LS-SVM)算法

LS-SVM是支持向量机的一种变形,它把不等式约束转化成等式约束,简化求解过程的复杂性。

假定汽油机瞬态工况空燃比的n个训练样本集为{(xi,yi)}(i=1,2,…,n),设线性回归函数为:

f(x)=wTφ(x)+b

(10)

其中,b为偏置量;w为权值向量。

引入结构风险函数,将(10)式回归问题转化为(11)式的二次优化问题,即

s.t.yi=wTφ(x)+b+ζi

(11)

其中,γ为正规则化参数;ζi为误差变量。

定义拉格朗日函数为:

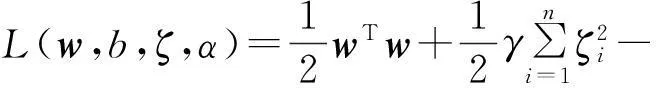
(12)

其中,αi为拉格朗日乘子。根据KKT条件可得:

∂L/∂ζi=0→αi=γζi,

∂L/∂αi=0→wTφ(xi)+b+ζi-yi=0

(13)

根据Mereer条件K(xi,xj)=φ(xi)Tφ(xj),建立汽油机空燃比LS-SVM预测模型为:

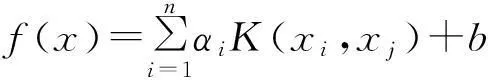
(14)

2.2　混沌时序LS-SVM预测模型

采用高斯RBF核函数作为瞬态工况空燃比LS-SVM预测模型的核函数[14-15],得到LS-SVM空燃比预测模型表达式为:

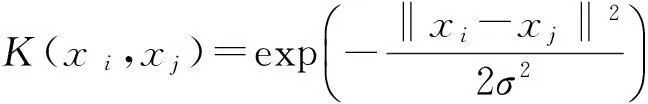
(15)

其中,σ为核函数的宽度参数;xi为训练样本数据;xj为核函数的中心。

由于超参数γ和核参数σ2对于提高LS-SVM的预测精度及泛化能力有重要作用,因此本文为使γ和σ2能在全局范围快速达到最优,利用混沌模型对2个参数取混沌变量,有效地降低LS-SVM模型的误差和提高其泛化能力, Logistic映射混沌模型[16]具体描述如下:

xk+1=μxk(1+xk),k=0,1,…,K；

μ∈[0,4]；x0∈(0,1)

(16)

当Lyapunov指数λ可取最大时,μ=4,λmax=ln 2=0.693 1,λ>0,Logistic映射方程处于完全混沌状态,系统输入xk∈(0,1),输出在(0,1)区间有遍历性。

混沌时序LS-SVM预测模型原理图如图 1所示。

图1　混沌时序LS-SVM预测模型原理图

3试验仿真及误差分析

3.1　试验仿真

本文选择某四缸电喷机为试验机,并建立发动机平均值模型。以主控PC、PCI2003 型数据采集卡作为数据采集平台,采集周期为100 ms, 在试验仿真过程中,需充分考虑节气门开度、喷油脉冲宽度、发动机转速及进气管压等信号对空燃比预测精确度的影响,因此,同时采集空燃比、节气门开度、进气管压、发动机转速及喷油脉冲宽度等信号。

在试验数据采集过程中,为简化发动机瞬态工况的复杂性,在节气门全程范围内,将试验分为加速(节气门由怠速位置开启至85%的开度)和减速(节气门由85%的开度减速至怠速位置)2个阶段分别进行,试验数据采集时间都设置为5 s,每个阶段分别采集5×500组试验数据;然后利用相空间重构技术对上述采集的试验数据进行重构, 每阶段各得8×500组数据;在每阶段中,任意选取6×500组数据为训练样本,2×500组数据为校验样本,分别采用LS-SVM模型、Elman 网络及BP网络进行仿真。Elman 网络拓扑结构为 8-12-6-1, Sigmoid为激活函数；BP网络拓扑结构选为8-6-1,共3层结构形式。加速和减速瞬态工况时,混沌时序LS-SVM预测结果与标定值的比较如图2所示。

图2　混沌时序LS-SVM预测结果与标定值的比较

3.2　各模型误差分析及比较

为定量评估混沌时序LS-SVM、Elman神经网络及前馈BP神经网络模型预测的准确性,本文通过平均相对误差(MRE)、均方根误差(RMSE)及平均绝对误差(MAE)对3种预测模型进行分析比较,误差表达式定义如下:

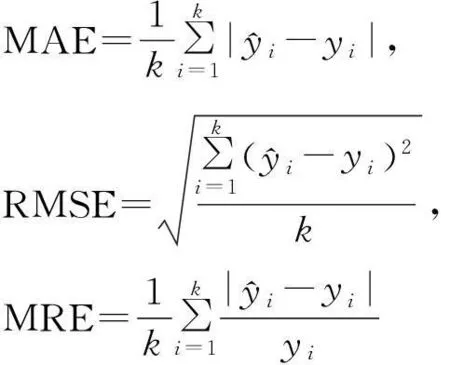
(17)

加速和减速瞬态工况时,LS-SVM、Elman网络及前馈BP网络误差比较结果分别见表1和表2所列。

由表1和表2可知,混沌时序LS-SVM预测模型在平均相对误差方面比Elman提高了近7%、比BP网络提高了近8%,收敛速度上比Elman神经网络模型及前馈BP神经网络模型提高了近32 s。

表1　加速瞬态工况各模型误差比较

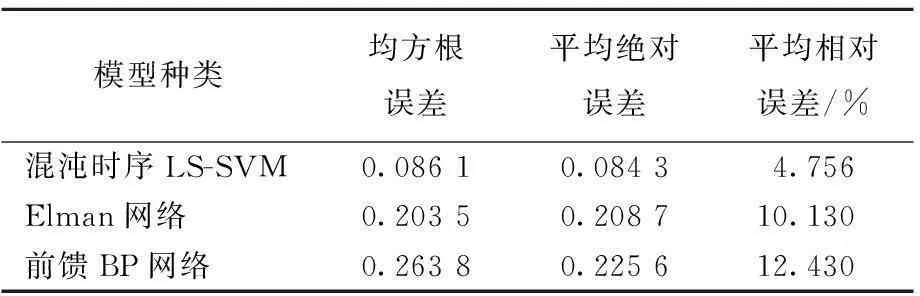
表2　减速瞬态工况各模型误差比较

加速和减速瞬态工况时,LS-SVM预测结果与Elman及BP网络的比较如图3所示。

图2和图3的仿真结果表明，混沌时序LS-SVM模型的精度优于Elman网络及前馈BP网络,混沌时序LS-SVM预测模型克服了神经网络的过拟合、泛化能力差以及易陷入局部极小值等缺点。

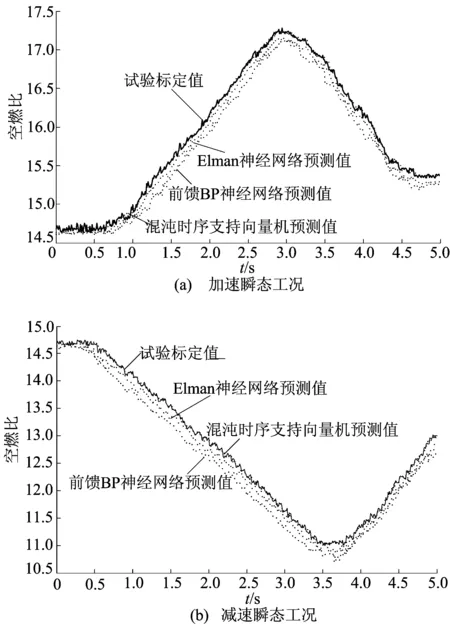
图3　LS-SVM预测结果与Elman及BP网络的比较

4结束语

针对汽油机发动机系统的高度非线性特性,本文提出了瞬态空燃比的LS-SVM预测模型。首先对瞬态空燃比时间序列进行了混沌识别,然后对试验数据进行相空间重构,并利用LS-SVM模型进行预测,最后得到LS-SVM模型的预测值。试验仿真表明:LS-SVM模型有效地提高了空燃比预测精度;与Elman网络及前馈BP网络相比,LS-SVM模型具有更强的非线性预测能力,更好的学习、泛化能力;在瞬态工况空燃比这种不确定性的非线性系统中混沌时序LS-SVM预测模型有很高的应用价值。

[参考文献]

[1]石屹然,田彦涛,张立,等.SI发动机空燃比联合非线性模型预测控制[J]. 吉林大学学报:工学版,2014,44(3):726-734.

[2]申福林,张勇,郭金刚.汽车燃油空气加热器燃烧排放控制研究[J].中国公路学报,2005,18(4):1153-1158.

[3]李岳林,孙祝宽,张雨,等.汽油机瞬态排放信号测试与特征分析的新动向[J].交通运输工程学报,2001,1(2):52-56.

[4]汪明磊,陈无畏,王家恩.智能车辆车道保持系统中避障路径规划[J]. 合肥工业大学学报:自然科学版,2014,37(2):129-133.

[5]Zhai Y J, Yu D L. Neural network model-based automotive engine air/fuel ratio control and robustness evaluation[J]. Engineering Applications of Artificial Intelligence, 2009, 22(2):171-180.

[6]侯志祥,申群太,吴义虎,等.基于Elman神经网络的车用汽油机过渡工况空燃比辨识[J].中国公路学报,2006,19(6):113-117.

[7]周能辉,谢辉,赵华,等.基于神经网络的汽油HCCI发动机空燃比控制策略[J].农业机械学报,2009,40(6):2-5.

[8]吴义虎,侯志祥,申群太.基于神经网络的车用汽油机过渡工况空燃比辨识[J].车用发动机,2007(2):40-43.

[9]张学工.关于统计学习理论与向量机[J].自动化学报,2000,26(1):32-43.

[10]Takens F. On the numerical determination of the dimension of an attractor[M]//Dynamical Systems and Bifurcations.Heidelberg:Springer,1985,1125:99-106.

[11]Grassberger P, Procaccia I. Measuring the strangeness of strange attractors[J]. Theory of Chaotic Attractors, 1983, 9(1/2):189-208.

[12]吕金虎,占勇,陆君安.电力系统短期负荷预测的非线性混沌改进模型[J].中国电机工程学报,2000,20(12):80-83.

[13]徐东辉,李岳林,杨巍,等.基于混沌RBF神经网络的汽油机进气流量预测研究[J].计算机工程与应用,2014,50(1):222-226.

[14]Zhang Junli,Zhou Guo, Zhou Yongquan.A new artificial glowworm swarm optimization algorithm based on chaos method [M]//Quantitative Logic and Soft Computing Vol 2.Springer,2010:683-693.

[15]何俊学.基于LS-SVM的软件可靠性模型研究[D].兰州:兰州理工大学,2009.

[16]Wong P K, Wong H C, Vong C M. Online time-sequence incremental and decremental least squares support vector machines for engine air-ratio prediction[J]. International Journal of Engine Research, 2012, 13(1):28-40.

(责任编辑胡亚敏)

Study of chaotic time series LS-SVM prediction of

gasoline engine transient air-fuel ratio

XU Dong-hui1,2，DAI Ji-yang3

(1.College of Physical Science and Engineering Technology, Yichun University, Yichun 336000, China; 2.Key Laboratory of Lightweight and Reliability Technology for Engineering Vehicle in Colleges of Hunan Province, Changsha University of Science and Technology, Changsha 410076, China; 3.School of Information Engineering, Nanchang Hangkong University, Nanchang 330063, China)

Abstract:In the process of feedback control of gasoline engine transient air-fuel ratio, the oxygen sensor has transmission delay and can not feed back the true value of gasoline engine transient air-fuel ratio quickly, thus failing in real-time control of transient air-fuel ratio. In this paper, the chaotic time series least squares-support vector machine(LS-SVM) prediction model of the gasoline engine transient air-fuel ratio is proposed. First, the original data are reconstructed by using phase-space reconstruction technique so as to recover the multidimensional nonlinear characteristics of time sequence of gasoline engine transient air-fuel ratio. Then LS-SVM is applied to training and identifying the reconstructed data. Finally, the air-fuel ratio identification results are obtained. The simulation results show that compared with the Elman neural network and feedforward BP neural network prediction models, the chaotic time series LS-SVM prediction model has stronger nonlinear prediction capability, and it can improve the prediction precision of transient air-fuel ratio effectively. This study can provide a basis for precise feedback control of transient air-fuel ratio.

Key words:transient condition; air-fuel ratio; least squares-support vector machine(LS-SVM) prediction model; phase-space reconstruction; prediction

doi:10.3969/j.issn.1003-5060.2015.11.005

作者简介：黄长清(1964-),男，湖南衡山人，博士，中南大学副教授，硕士生导师.

基金项目：国家自然科学基金资助项目(51275533)

收稿日期：2014-11-06；修回日期：2014-12-25

中图分类号:U464.171

文献标识码：A

文章编号：1003-5060(2015)11-1458-05