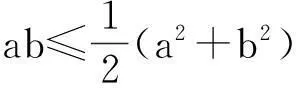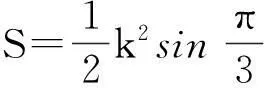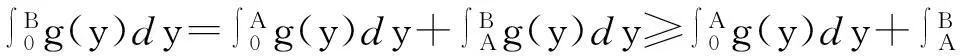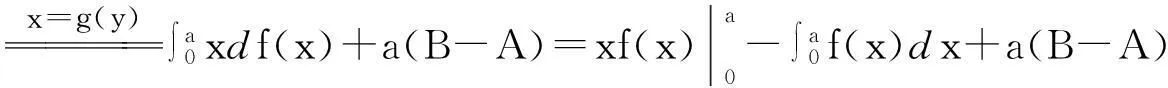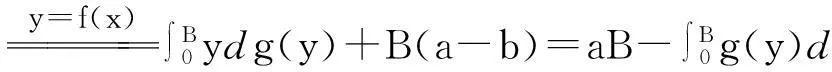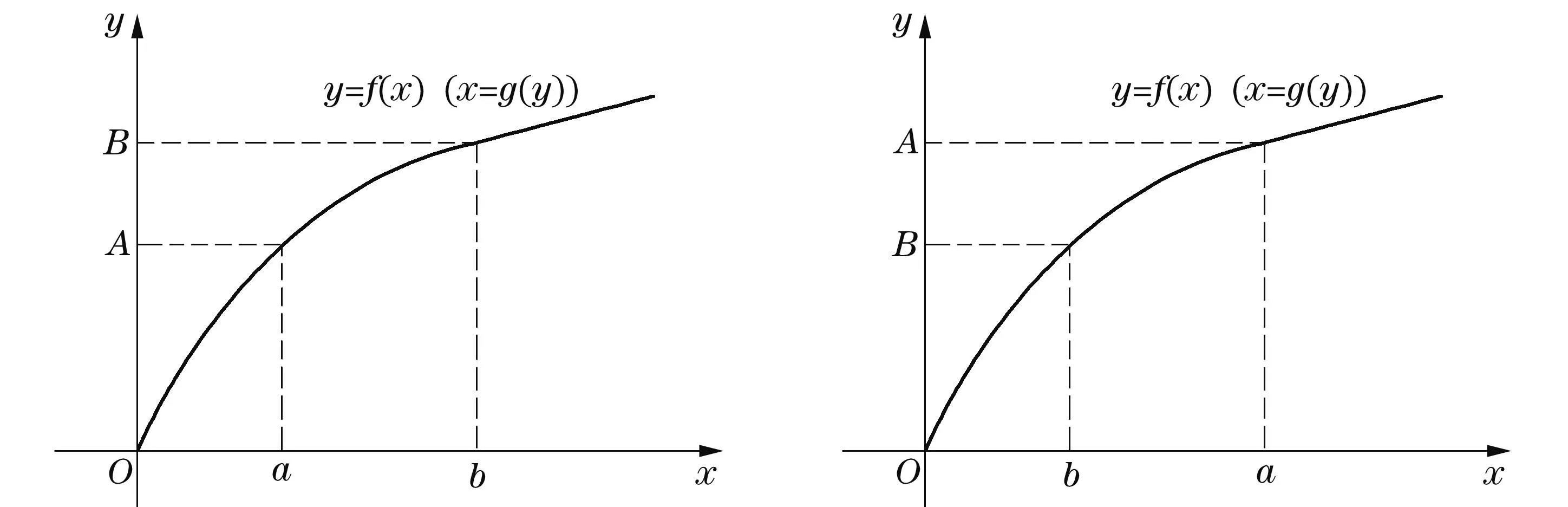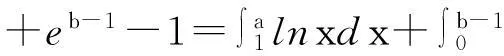依托面积为载体的几个不等式的直观证明及思考

陈建华

(扬州大学数学科学学院，江苏扬州225002)



依托面积为载体的几个不等式的直观证明及思考

陈建华

(扬州大学数学科学学院，江苏扬州225002)

[摘要]依托面积为载体，在给出Young不等式的几何直观证明的基础上，继续讨论几何直观在几个相关不等式证明中的运用.探讨了数学教学中如何发挥几何直观的作用.

[关键词]不等式； 几何直观； 面积

1Young不等式

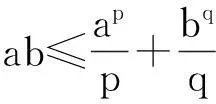
(1)

(1)式被称为Young不等式.

Young不等式是证明Hölder不等式、闵科夫斯基不等式的基础，也是定义向量(矩阵)P-范数的关键.关于该不等式的证明，矩阵论和泛函分析课程中都是构造辅助函数来证明的.如：史荣昌等构造

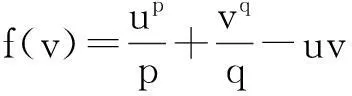
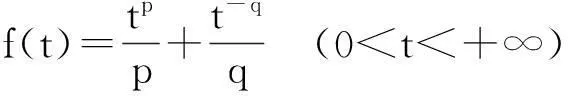
求导取特殊值证明[2]；文献[3]和[4]中，戴华与程其襄、张奠宙等都是构造的辅助函数是f(x)=xα-αx，这里x>0,0<α<1，然后证明函数在x=1时取得最大值1-α.教学中，我们发现构造辅助函数证明不等式是有效的，但均较为抽象，特别是后两个辅助函数不易想到，从教学角度看，这些辅助函数就像“天上掉下来的林妹妹”，给人的感觉就是突然.如何改变知识形态，让学生易于接受，有利于学生学习呢？本文以平面图形面积为载体，从几何直观的角度作了一些思考.

2直观证明

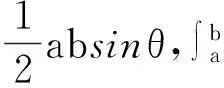
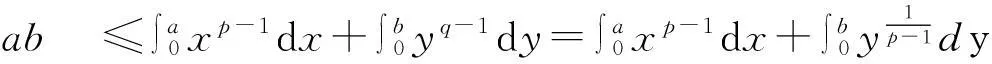
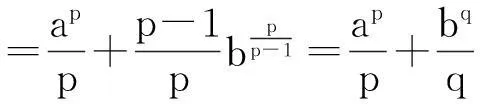
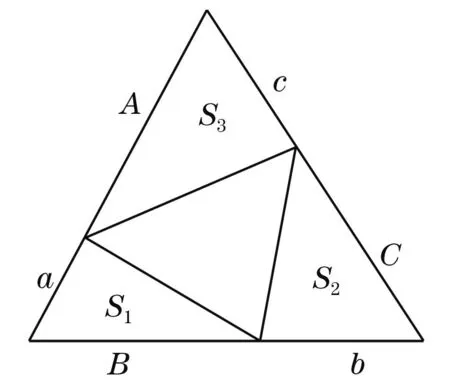
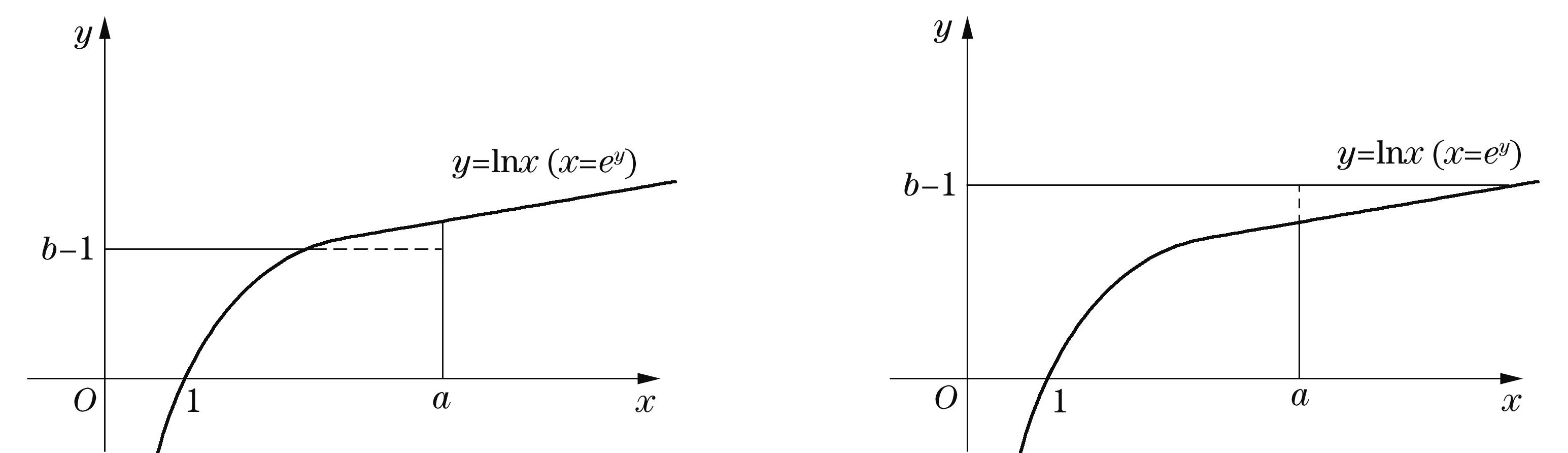
图1　(p>2)　　　　　　　　　　　　　　　　　　图2　(1

教学实践表明较之于照本宣科使用辅助函数讲解，学生们对基于面积的几何直观证明方法更感兴趣，更容易接受.我的感受是：抽象的知识会加大学生的认知难度，而教师将抽象的知识以形象化的状态呈现出来，教学中就会使得教师授课轻松，学生对知识的理解透彻、记忆深刻，掌握牢固.正像斯蒂思曾经说过的：如果一个特定的问题可以被转化为一个图形，那么，思想上就整体地把握了问题，并且能创造性地思索问题的解法[5].

3特殊化分析

由Young不等式，有

推论1当p=q=2时，得基本不等式

(2)

当a=x,b=1时，得

(3)

图3

数学教学中，关于挖掘不等式中固有的几何直观因素，创造贴切的几何直观来理解不等式的经典案例有许多.譬如第21届全苏数学竞赛八年级试题：

命题1设a,b,c,A,B,C为正实数，且满足关系a+A=b+B=c+C=k，则有不等式

aB+bC+cA

成立.

分析由条件a+A=b+B=c+C=k>0，结论中aB,bC,cA,k2，引领我们将“面积”纳入思考的范围，而三组数的和相等，让正三角形或正方形浮现在我们面前.如图4，构造边长为k的正三角形，则有大三角形的面积为

图4

另外含三角形顶点的三个小三角形的面积分别为

而它们的关系S1+S2+S3

这里一图抵百语，几何直观图形把不等式反映的数量关系，简明直观地呈现出来.用到的几何知识只有三角形的面积公式，问题解决的关键是构造正三角形.获得的几何证法简洁明快，直观有趣，学生易于理解.如果局限在代数范围内考虑问题，则需要较好的因式组合、不等式放缩的基本功.下面是一种代数证法：

k3=(a+A)(b+B)(c+C)

=abc+Abc+acB+ABc+abC+AbC+aBC+ABC

=abc+ABC+aB(c+C)+cA(b+B)+aC(b+B)

>aBk+cAk+aCk=(aB+cA+aC)k.

因为k>0，故不等式成立.

4一般化探讨

Young不等式一般化，有下列结论：

定理2设函数f(x)在[0,+∞)上可导，严格单调，且f(x)→ +∞(x→+∞),f(0)=0，则对任意实数a≥0,B≥0，有下列不等式

(4)

成立，其中g(y)是f(x)的反函数.

证对任意给定的实数a,B，设A=f(a),f(b)=B(这里b唯一确定).

(i) 当b>a时，有B>A，如图5，当y≥A时，g(y)≥a，于是

所以

(ii)当b≤a时，有B≤A，如图6，当x≥b时，f(x)≥B，于是

图5　(b>a)　　　　　　　　　　　　　　　　　　　图6　(b

命题2设a≥1,b≥1，则有不等式ab≤alna+eb-1成立.

分析考虑用几何直观解题，不等式左边联系长方形的面积，右边是两个平面图形面积之和，由于这两个平面图形未必是直线型的，自然联系定积分考虑，关键是需要考虑对应积分的被积函数是谁？还有积分区间如何确定？

证用几何直观解题，对于不等式右边第一项alna，对应定积分的被积函数是lnx，且积分区间[1,a]，这样需要凑出一项

同样，ea-1联系的定积分的被积函数是ey，且积分区间[0,b-1]，则有

这样不等式左边对应一长方形的面积，值为ab-a.调整不等式为

ab-a≤(alna-a+1)+(eb-1-1).

即

由于y=lnx,y=ex互为反函数，作出函数图形(如图7，图8)

图7　　　　　　　　　　　　　　　　　　　　　　　图8

从图形直观立即知道不等式成立.

综上，从问题的几何特征寻找不等式的几何表征，展示问题的本质，让不等式的证明过程避开了代数的繁琐计算或构造辅助函数的抽象，有利于学生对不等式的深刻理解.

5教学启示

以上利用几何直观分析了若干不等式，说明借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果.如何联想问题的几何直观背景，对几何直观内涵把握得更为细致与深入，谈几点看法，与同仁交流切磋.

第一，几何直观是获得对数学深度理解的依托.数学教学中，定义不是概念表征的主要形式，解析式也未必是命题表征的关键形式.数学中有许多抽象的概念、公式、不等式、方程乃至一些重要性质、定理都有其具体的几何意义.罗巴切夫斯基断言“直线外的一点可以作多条平行线”、“ 三角形的内角和不一定是180度”也是直到在欧氏空间找到可视的直观模型才获得认可.数学教学中，如果能将抽象的数学知识中固有的几何直观表现提供给学生，创造丰富的几何直观，让它们弥漫在数学学习的细节处、关键处，就能帮助学生真正将新的知识融入学生已有的认知结构，获得意义.

第二，几何直观是推动思维展开的基础.徐利治先生认为，直观就是借助于经验、观察、测试或类比联想，所产生的对事物关系直接的感知与认识，而几何直观是借助于见到的或想到的几何图形的形象关系产生对数量关系的直接感知.这给了我们一种理念上的拓展，即几何直观不只是事物的形象化呈现和形式化演示，还是一种思维方式.英国数学家Grlffiths在讨论数学中的直觉和领悟时曾提出，数学中最常用的思维媒介是数学结构的模型和实例，对于初学者来说，几何图形比代数符号更容易掌握和接受[6].研究表明思维的展开更倾向于依据直观形象.数学教学中，如何把几何直观内化为学生的思维习惯，是我们每一个数学教师应该关心的问题.

第三，几何直观是开展数学活动的一种技能.现代数学的发展，使得数学许多分支渐渐远离生活源泉，不断发展的形式化使得数学愈来愈抽象，学生的数学学习愈来愈困难，而几何仍然保持着与现实生活直接而又丰富的联系.数学教学实践告诉我们，适时捕捉数学问题中固有的、内在的几何直观性，体会如何直观化是一种数学能力.这种能力会引导学生思维的展开，方法的形成.几何直观教学在数学教学上是必须注重的一个重要的教学环节.

古代诗人王籍在他的《如若耶溪》中有诗句“蝉噪林更静，鸟鸣山更幽”，动态反衬静态，这和几何直观用于证明不等式，在意境是相通的.几何直观是一种意识，一种思维方式，也是一种技能，中小学生需要，大学生和研究生同样需要.加强几何直观教学吧，它能够让我们的数学教学中“天上掉下来的林妹妹”的现象少一些，更少一些.

[参考文献]

[1]史荣昌，魏丰．矩阵分析[M]．北京：北京理工大学出版社，2010:178.

[2]徐仲，张凯院，陆全，冷国伟．矩阵论简明教程[M]．北京：科学出版社，2005:37-38.

[3]戴华．矩阵论[M]．北京：科学出版社，2007:170-171.

[4]程其襄，张奠宙，魏国强，等．实变函数与泛函分析基础[M]．北京：高等教育出版社，1988:198-199.

[5]绍盖 G．几何直观在数学中的作用[J]．数学通报，1982,(2):21-23.

[6]李士錡．PME：数学教育心理[M]．上海：华东师范大学出版社，2001:41.

[7]孔凡哲，史宁中．关于几何直观的含义与表现形式[J]．课程·教材·教法，2012,32(7):92-97.

[8]王敬庚．论几何直观与高师数学教学[J]．数学教育学报，1993,2(1):75-80.

[9]李晓莉．借助几何直观证明一类积分不等式[J]．西安邮电学院学报,2003,8(3):73-75.

Intuitive Proof and Thinking of Some Inequality Depends on Area

CHENJian-hua

(School of Mathematics Science, Yangzhou University, Yangzhou Jiangsu 225002,China)

Abstract:Based on the area as the carrier, this paper continues to discuss the geometry intuition in the application of several related inequality proofs on the basis of giving the geometric intuition proof of young inequality. This paper discusses how to play the role of geometric intuition in the mathematics teaching.

Key words:inequality; geometric intuition; area

[中图分类号]O151.21； G642.4

[文献标识码]C

[文章编号]1672-1454(2015)05-0060-06

[基金项目]国家自然科学基金项目(11471282)； 江苏省研究生教改课题(JGLX14-1310)

[收稿日期]2015-08-21