牛顿-莱布尼兹公式与泰勒公式的拓展与应用
2016-01-28韩茂安
韩茂安
(上海师范大学数学研究所,上海200234)
牛顿-莱布尼兹公式与泰勒公式的拓展与应用
韩茂安
(上海师范大学数学研究所,上海200234)
[摘要]探讨牛顿—莱布尼兹公式和泰勒公式对含参数函数的拓展形式,并用来研究含参数函数的零点的个数和微分方程周期解的个数的判定问题.
[关键词]牛顿—莱布尼兹公式; 泰勒公式; 周期解
1基本定理
众所周知,牛顿-莱布尼兹公式是说,如果F∶[a,b]→R具有连续导数,则成立
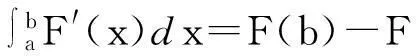
这一公式被誉为微积分学基本定理[1].如果设x=a+t(b-a),则上式成为
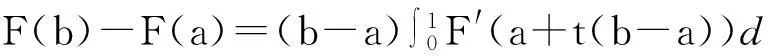
(1.1)
现在我们对高阶可微函数应用(1.1).设U为x=0的一邻域,一元函数F在U上有直到r阶的连续导数,r≥1,记为F∈Cr(U).利用公式(1.1),可将函数F写为
F(x)=F(0)+xF0(x),
(1.2)
其中


引理1.1设U为x=0的邻域,F∈Cr(U),r≥1,则(1.2)成立,其中
F0∈Cr-1(U),F0(0)=F′(0).
现设m为一自然数,m≥0,并设F∈Cm+1(U),则由带积分形式余项的泰勒公式可知
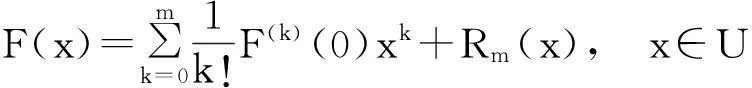
其中
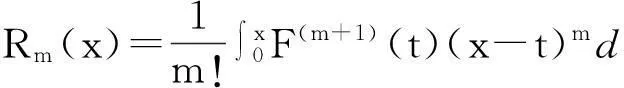
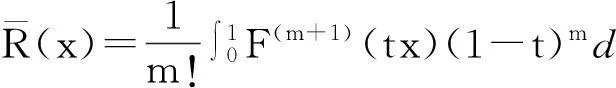
(1.3)
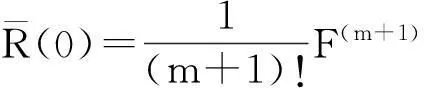
于是,证明了下述引理.
引理1.2设U为x=0的邻域,F∈Cm+1(U),m≥0,则有

且
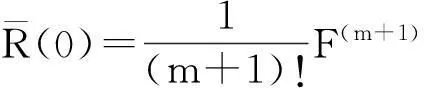
现在,把上述两个引理的结论拓展到多元函数.设有多元函数F(x,y),x∈U,y∈D,U为x=0的邻域,D⊂n,n≥1.如果F∈Cr(U×D),则F对应用引理1.1可得
F(x,y)=F(0,y)+xF0(x,y),
(1.4)
其中

与引理1.1类似,利用含参量积分的可微性知F0∈Cr-1(U×D).事实上,这里需要先建立含向量参数的积分之可微性定理,然后再多次利用这一定理得到这一结论.于是,证得下述定理.
定理1.1设F∈Cr(U×D),其中U为x=0的邻域,D⊂n,n≥1,则(1.4)成立,其中

同理,利用引理1.2以及含参量积分的连续性定理知成立下述定理.
定理1.2设F∈Cm+1(U×D),U为x=0的邻域,D⊂n,n≥1,m≥0,则有
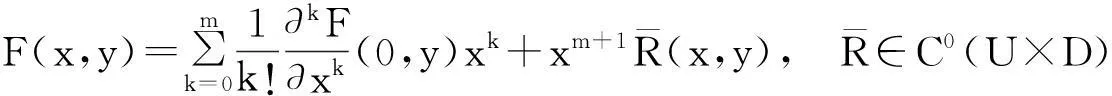
且
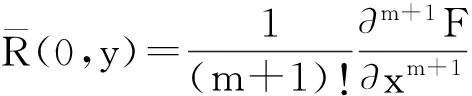
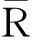
2含参数函数根的个数
定理2.1设存在自然数m≥0,使F∈Cm+1(U×D),那么成立
(i) 如果
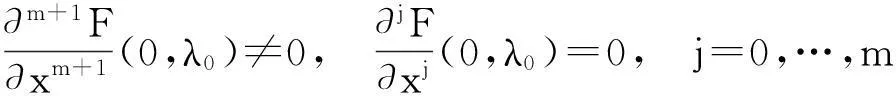
则存在ε0∈(0,ε),使当|λ-λ0|<ε0时,F关于x在区间(-ε0,ε0)上至多有m+1个根.
(ii) 如果进一步设

其中
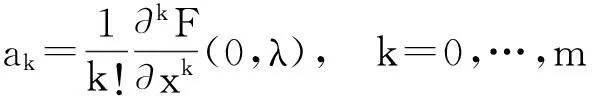
则对任意δ∈(0,ε0),都存在λ满足|λ-λ0|<ε0,使函数F(x,λ)关于x在区间(-δ,δ)内出现m+1个根,且均为单根. 此外,这m+1个根可以全部是正根.
证在研究平面系统Hopf分支中极限环的个数问题时需要用到上述两个结论(却并没有将它们专门写成定理的形式),见[3,4]. 但以往都是对C∞函数来论述的(因为所讨论的平面系统都假定是C∞光滑的),上述结论则不要求C∞光滑,这一点与以往不同.而对C∞光滑的情况,结论(i)可用反证法和罗尔定理来证,对结论(ii),先用一次隐函数定理,然后有两种证法,一是逐次改变系数的符号使函数值不断变号,每变号一次就出现一个根,二是引入合适的参变量尺度变换,而后利用多项式和连续函数的性质,一下子获得m+1个根. 这里我们提供一种新的证法,即用数学归纳法来证明.
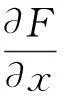
再证结论(ii).利用定理1.2可知成立

(2.1)
且
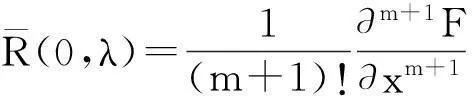
由隐函数定理知道,结论(ii)中的条件意味着式(2.1)中的系数aj可取为自由参数. 因此,现设这m+1个系数均为自由参数,并用归纳法来完成证明. 当m=0时,式(2.1)成为

且


不妨设它为正.则存在x0>0,使当a0=0时F(x0,λ)>0,当|x|≤|x0|时

从而当0<-a0≪1时
F(x0,λ)>0,F(0,λ)=a0<0.
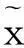
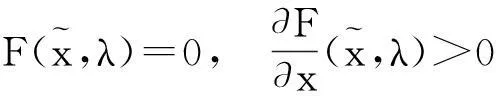
即F有一个正的单根.
设已证结论对m=k-1成立,现设m=k,此时由(2.1)知
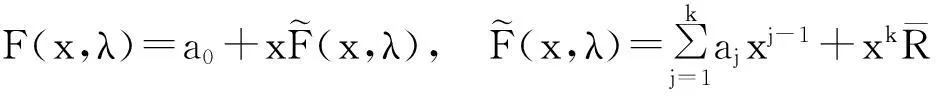
作为一个简单应用,由上述定理可知,C3函数
F(x,λ)=λ1+λ2x+λ3cosx+sinx+x10/3,
对λ0=(0,-1,0)附近的某些λ=(λ1,λ2,λ3)恰有3个正根.
3一维周期系统周期解的分支
本节利用定理1.1与定理2.1讨论一维周期系统周期解的个数和分支. 首先引入几个基本概念(详见[4]). 考虑一维微分系统
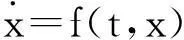
(3.1)


引理3.1设存在1≤k≤r使当|x|充分小时T周期系统(3.1)中的f满足
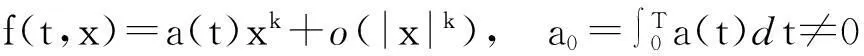
则

从而零解x=0为(3.1)的k重周期解.
证由于解x(t,x0)关于初值x0是Cr,故对充分小的|x0|,它可写成
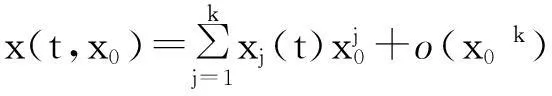
其中x1(0)=1,xj(0)=0,j≥1. 将上式代入(3.1)中,利用所设条件,易求得

由此即知结论成立.
下面给出方程(3.1)存在周期解族的条件.
引理 3.2如果T周期系统(3.1)中的f满足
f(-t,x)=-f(t,x),
(3.2)
则其任一有界解都是周期解. 特别,如果(3.2)成立,且存在正数M>0使对一切(t,x)都有
|f(t,x)|≤M(1+|x|),
(3.3)
则(3.1)的一切解都是周期解.

x(T/2,x0)=x(-T/2,x0).
由解的唯一性又知x(t+T,x0)=x(t,x(T,x0)),因此又有
x(T/2,x0)=x(-T/2,x(T,x0)),
从而成立
x(-T/2,x0)=x(-T/2,x(T,x0)),
于是必有x0=x(T,x0)=P(x0) (因为对任意t,x(t,x0)关于x0都是严格增加的,例见[4].)从而,这个解是周期的. 引理的后半部分利用常微分方程比较定理即得,因为任一周期线性方程的解都是有界的.
现考虑系统(3.1)的T周期扰动系统

(3.4)
其中f与f1关于t都是T周期的,都是Cr函数,且f1(t,x,0)=0. 系统(3.4)的Poincaré映射记为P(x0,λ),令
F(x0,λ)=P(x0,λ)-x0,
称函数F为(3.3)的后继函数或分支函数. 显然,分支函数关于x0的根与(3.4)的周期解是一一对应的,此外,由微分方程解对初值与参数的光滑性定理知,映射P与函数F都是Cr的.可证
定理3.1设存在1≤k≤r使得x=0是(3.1)的k重周期解,则存在ε>0,使得对一切|λ|<ε方程(3.4)在区域|x|<ε至多有k个周期解.
证由假设知
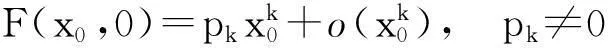
由此,利用定理2.1的结论(i)即得证明.
在具体应用中,可以利用定理2.1的结论(ii)证明,Ck系统的k重周期解在适当的Ck扰动下能够产生k个周期解,这里不再给出.
值得注意的是,定理3.1对系统的光滑性的要求已经降到最低. 为说明这一点,取k=r=1,利用隐函数定理易见,C1系统的单重周期解在C1扰动下只产生一个周期解.然而,如果扰动不是C1的,这一结论就不成立了. 例如

在x=0的任意小邻域内都可以出现3个周期解.
下面考虑周期解族的扰动.考虑T周期扰动系统
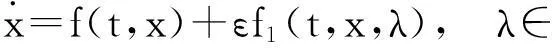
(3.5)
其中f与f1关于t都是T周期的,都是Cr函数,且f满足(3.2)与(3.3).系统(3.5)的Poincaré映射记为P(x0,ε,λ),后继函数为
F(x0,ε,λ)=P(x0,ε,λ)-x0.
由引理3.2知,F(x0,0,λ)=0,由微分方程解对初值与参数的光滑依赖性定理知函数F关于(x0,ε,λ)为Cr的,故由定理1.1知
定理3.2设Cr方程(3.5)满足(3.2)与(3.3),r≥1,则
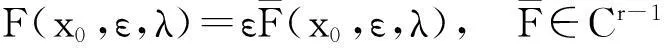
上述定理之结论好像是很显然的,但如果不利用定理1.1就难以给出其成立的理由.对平面系统闭轨族的扰动分支,可给出类似的结果,此地不再详论.
我们来考虑一类较具体的方程,即
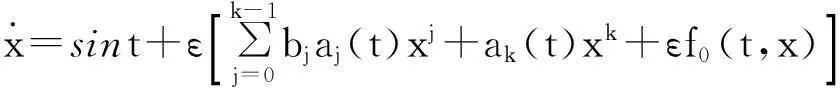
(3.6)
其中aj(t)为Ck+1类2π周期函数,j=0,1,…,k,f0(t,x)为关于t为2π周期的Ck+1类函数. 记b=(b0,…,bk-1),设x(t,x0,ε,b)为(3.6)的以x0为初值的解,则易知
x(t,x0,ε,b)=1-cost+x0+εx1(t,x0,b)+O(ε2),
其中
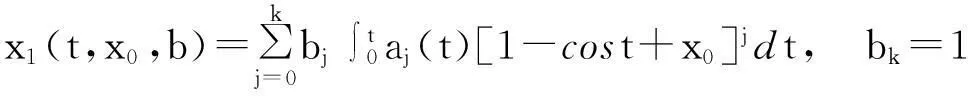
经整理,易知成立
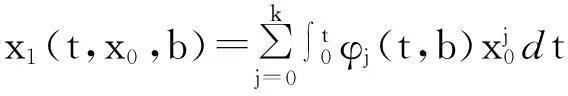
其中
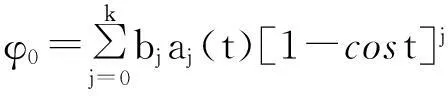
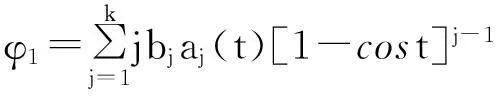
……
φk-1=bk-1ak-1(t)+kbkak(t)[1-cost],
φk=bkak(t).

现在假设

(3.7)
则有λk≠0,以及
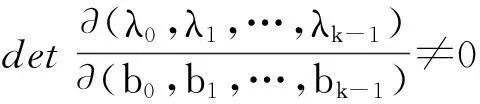
则由上述讨论,利用定理3.2和定理2.1可知在条件(3.7)下,存在向量b∈Rk使当ε充分小时方程(3.6)恰有k个2π周期解.
[参考文献]
[1]华东师范大学数学系. 数学分析(上册)[M]. 4版.北京: 高等教育出版社,2010.
[2]华东师范大学数学系. 数学分析(下册)[M]. 4版.北京: 高等教育出版社,2010.
[3]Han M. Bifurcation Theory of Limit Cycles [M]. Beijing: Science Press,2013.
[4]赵爱民,李美丽,韩茂安. 微分方程基本理论[M].北京:科学出版社,2013.
Extensions and Applications of
Newton-Leibniz’s figure and Taylor’s figure
HANMao-an
(The Institute of Mathematics, Shanghai Normal University, Shanghai 200234, China)
Abstract:We provide some extensions of Newton-Leibniz’s figure and Taylor’s figure to smooth functions with multiple variables. Then we present some interesting applications of these extensions to bifurcations of periodic solutions of differential equations.
Key words:Newton-Leibniz’s figure; Taylor’s figure; periodic solution
[中图分类号]O172
[文献标识码]A
[文章编号]1672-1454(2015)05-0006-06
[收稿日期]2015-06-19
