平板折叠桌最优设计的模型研究
2016-01-28张雪蕾王佳颖
张雪蕾, 王佳颖, 吴 雷
(1.北京师范大学数学科学学院,北京100875; 2.北京师范大学信息科学与技术学院,北京100875)
平板折叠桌最优设计的模型研究
张雪蕾1,王佳颖1,吴雷2
(1.北京师范大学数学科学学院,北京100875;2.北京师范大学信息科学与技术学院,北京100875)
[摘要]现有一种创意平板折叠桌.建立初等函数模型,给出折叠桌的动态变化过程及开槽长度和桌脚边缘线的函数表达;根据“稳固性、加工难易、用材多少”等要求建立多目标函数的优化模型,采用基于多目标函数的“模拟退火”算法,求得一定条件下的最优设计方案.最后给出一种折叠桌设计软件的初等目标函数数学模型,并利用次模型设计出三角形、六边形两种新的创意平板折叠桌.
[关键词]平板折叠桌; 动态变化过程; 设计加工参数; 优化问题; 约束条件下非线性多目标规划; 模拟退火算法
1引言
为了生活方便,而且富有创意,现设计一种可折叠的桌子.桌面呈圆形,桌腿可随着铰链的活动平摊成一张平板.桌腿由若干根木条组成,分成两组,每组各用一根钢筋将木条连接,钢筋两端分别固定在桌腿各组最外侧的两根木条上,并且沿木条有空槽以保证滑动的自由度.先就该折叠桌的动态变化过程、设计加工参数等方面建立数学模型进行讨论,考虑其最优化的设计加工参数,最后旨在给出一种折叠桌设计软件的数学模型,尽可能满足客户任意设定的要求而设计出折叠桌.
2圆形平板折叠桌设计模型
1.1 折叠桌动态变化过程模型
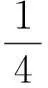

图1 平板桌示意图
在折叠过程中,将圆形桌面看作保持不动,桌腿上端点也确定,要描述折叠桌的动态变化过程,只需给出桌腿下端点的运动轨迹.本文以圆盘桌面的下表面圆心为原点,平行于长方形平板的长边为x轴,平行于宽边为y轴,垂直于板为z轴,建立3维的直角坐标系.
对于第n条桌腿,我们设其与x轴的夹角为φn,我们先考察长方形平板上桌面的及桌腿木条的分布情况.如桌面的俯视图图2所示,
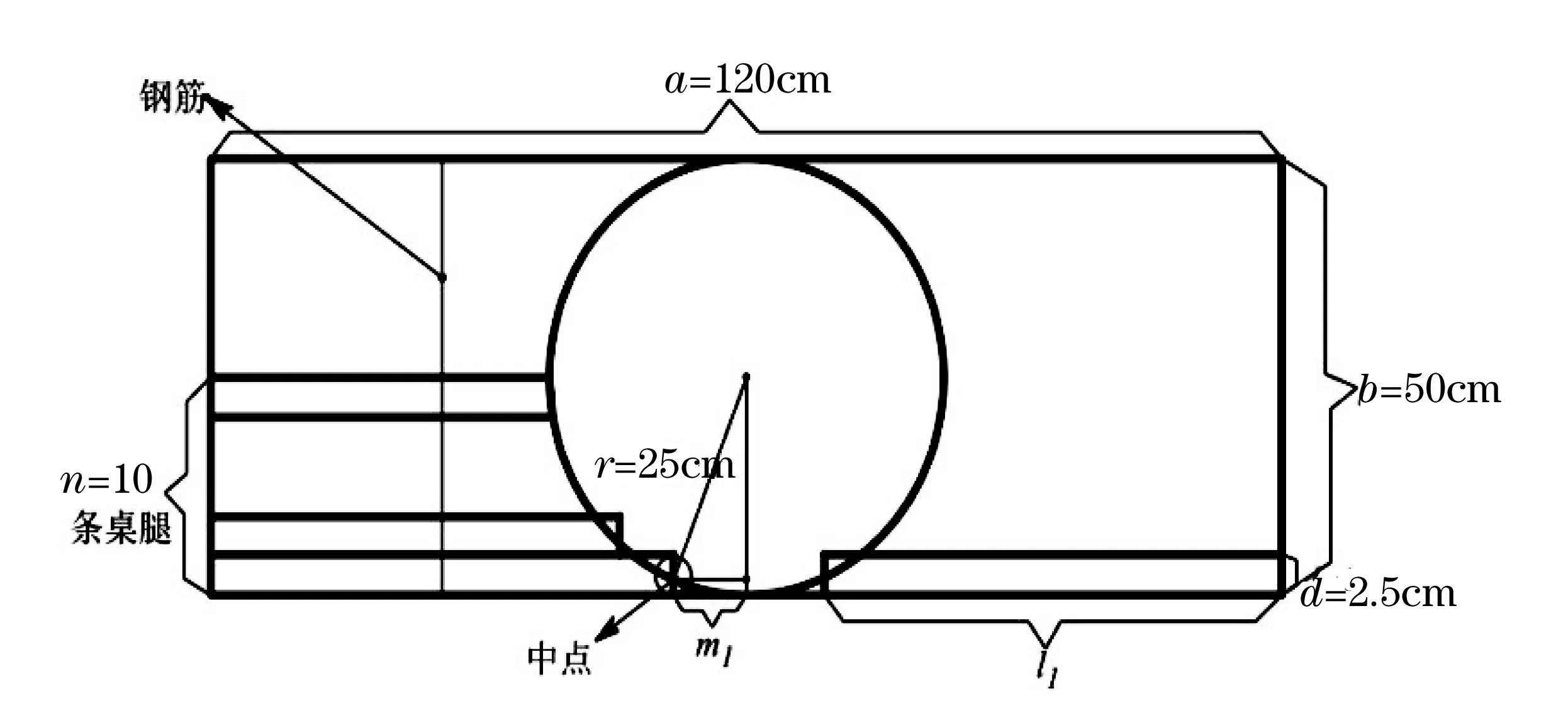
图2 平板桌俯视图
每根木条顶端到桌面直径的距离
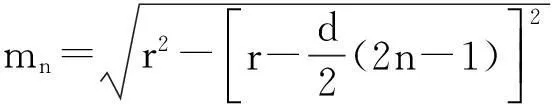
每根木条的长度
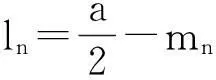
每根木板长如表1所示:

表1 每根木条的长度
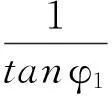
在折叠的某一过程中,每个桌腿下端点的坐标表示可根据图3求出.
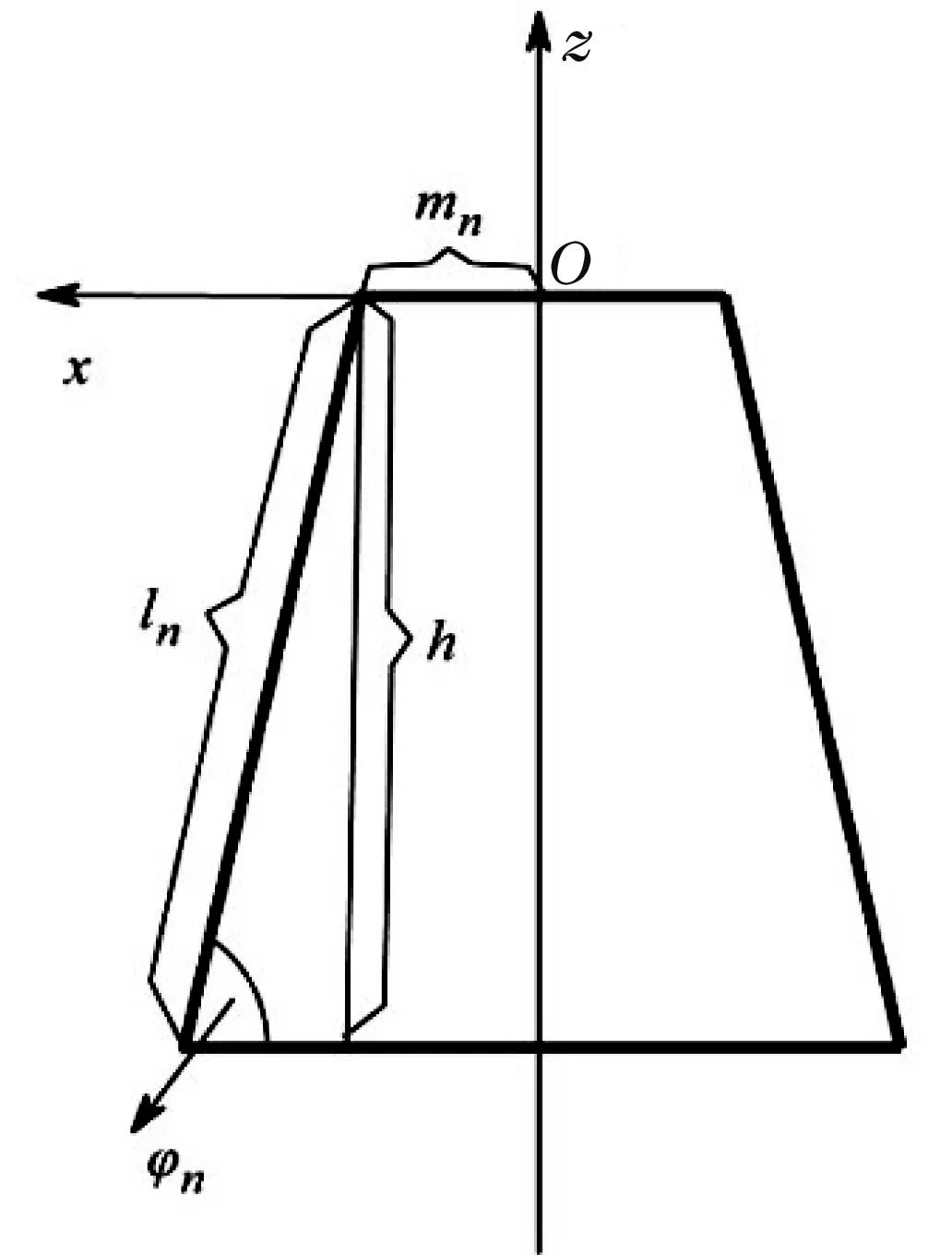
图3 平板桌侧视图
因此第n条桌腿下端点坐标表达的参数方程为
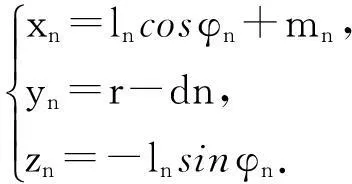
可以看出,该方程正好表示每条桌腿绕顶端做半径为桌腿长的圆周运动,与实际情况相符.
将ln和mn的表达式代入,得到最终的描述“折叠桌动态变化过程”的参数方程为
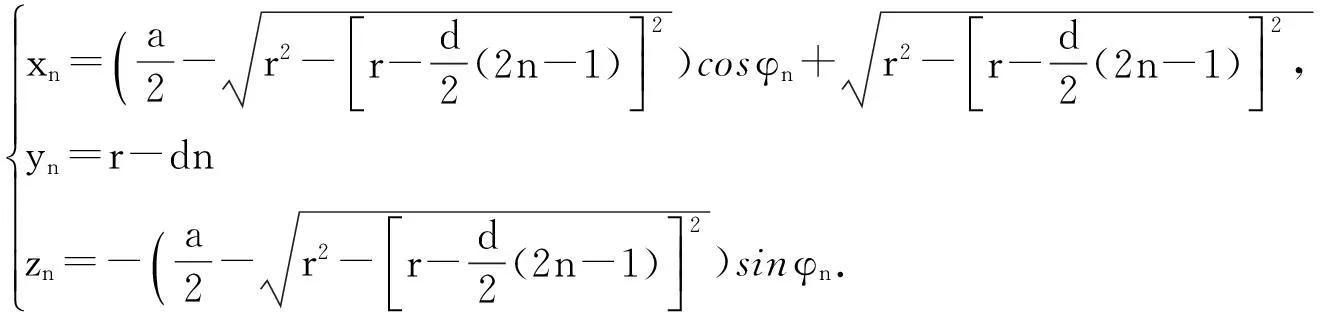
同时可根据如图4所示的几何关系,得到

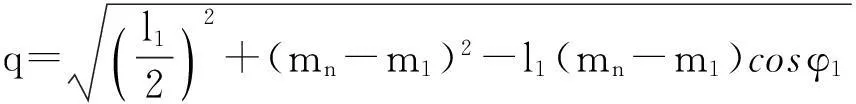

图4 平板桌侧视图
最后得到里面每根木条与地面夹角φn和最外侧木条与地面夹角φ1的关系
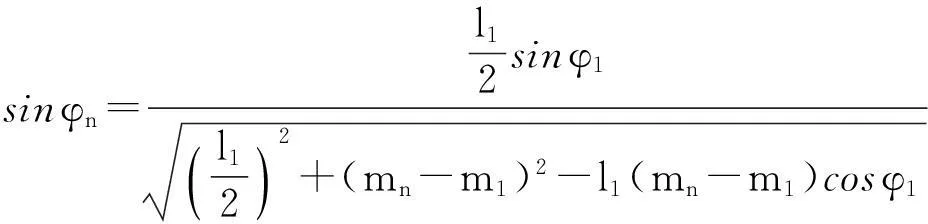
代入上述参数方程即可得仅含参数最外侧木条与地面夹角φ1与桌腿条数n的参数方程,即为最终的参数方程.(由于最终方程若将所有变量代入十分复杂,且无法清晰的展示各变量之间的关系,故没有展示出代入后的最终结果.)
具体动态变化过程图:
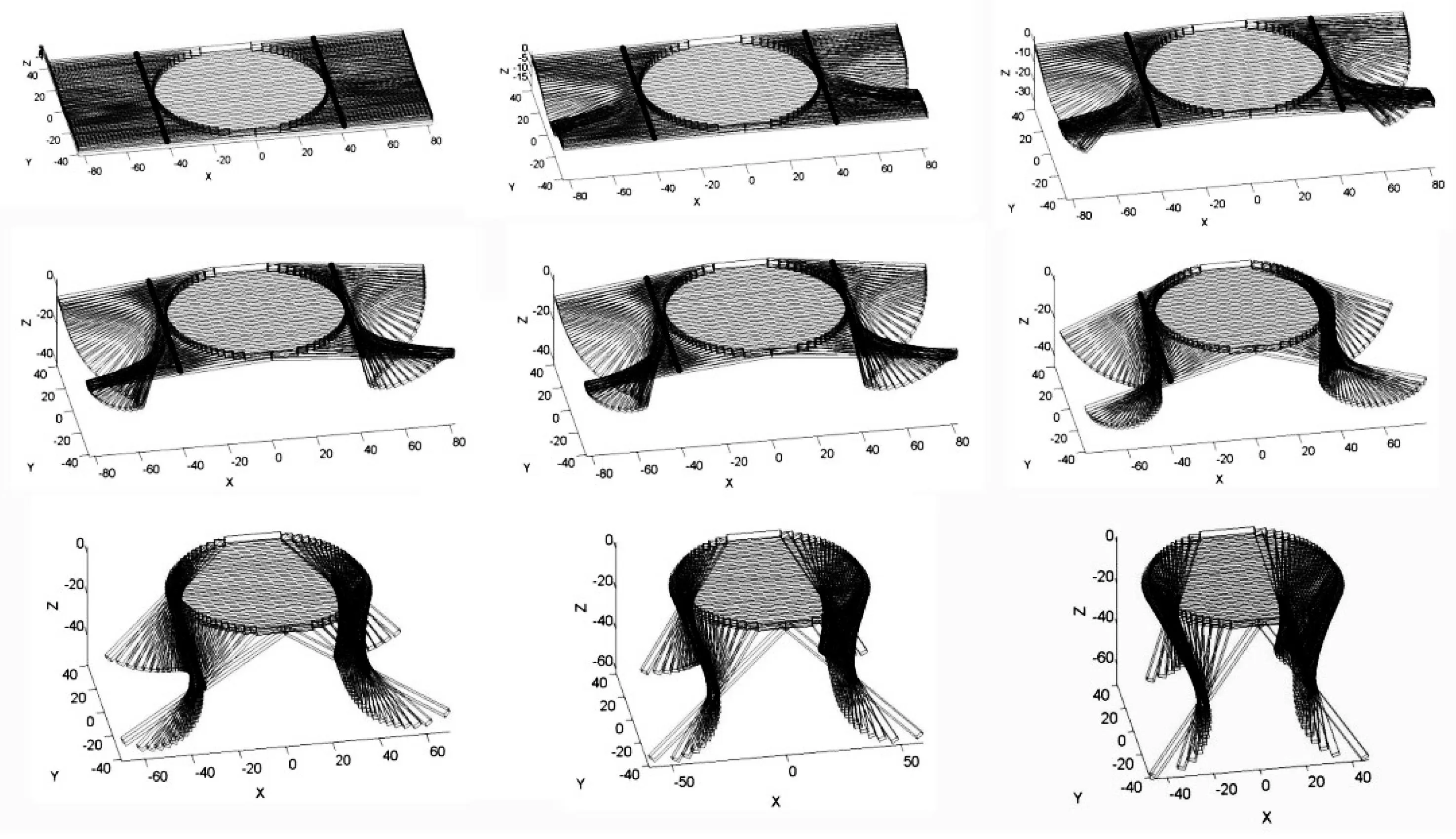
图5 动态变化过程图
2.2 木条开槽长度的数学描述
在折叠过程中,木条的开槽长度是很重要的设计加工参数.平板时钢筋所在的位置与折叠后钢筋所在位置的差值即为木条的开槽长度,通过每根木条折叠前与折叠后的几何关系(如图6所示)即可求出.
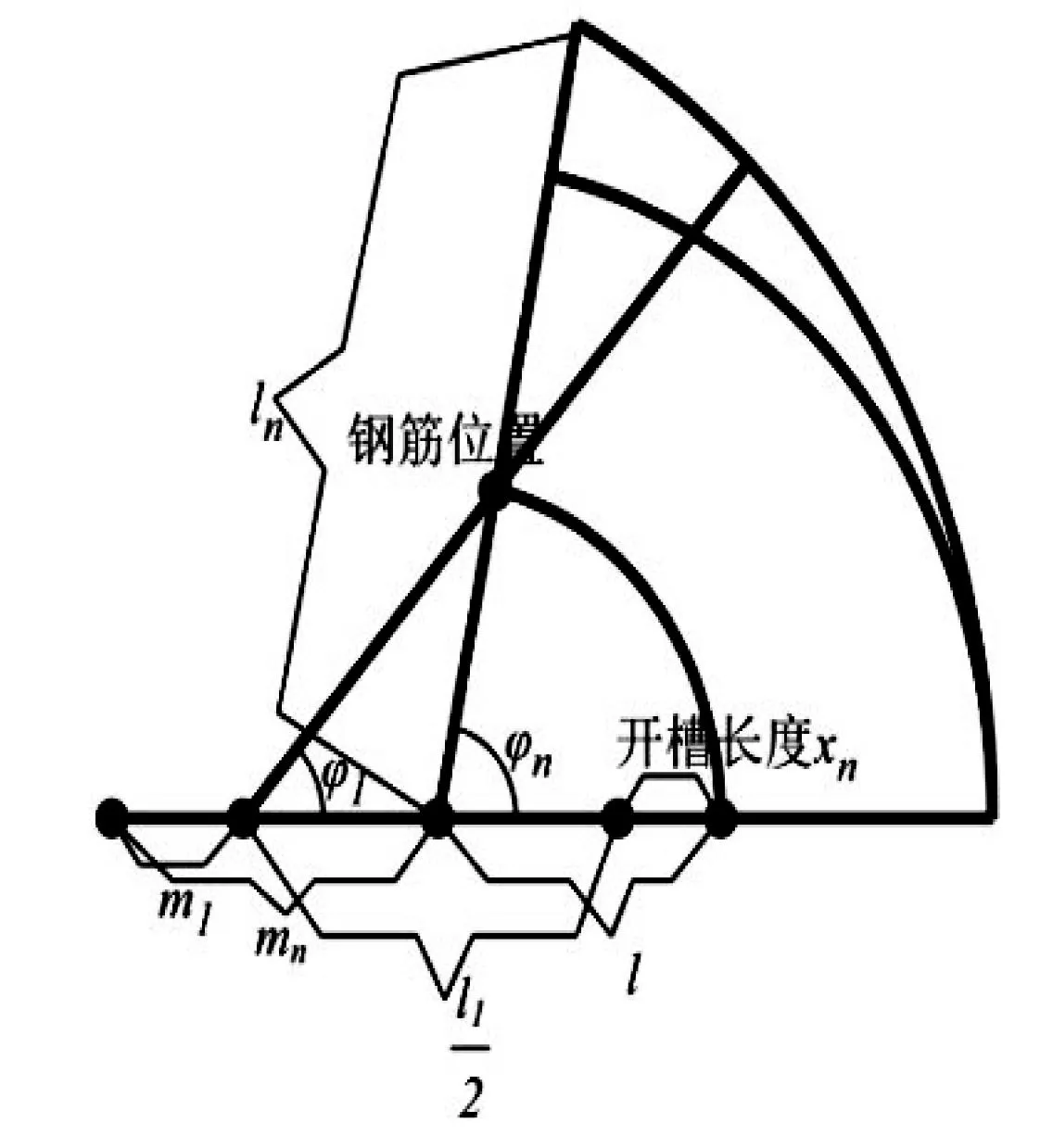
图6 平板桌侧视图
该图是最外侧木条转动φ1角度时的平面图,此时,第n根木条转动了φn角度,从图中很容易看出开槽长度
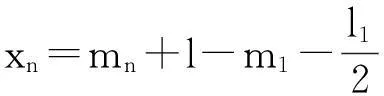
其中l与图2的q的长度相同,故
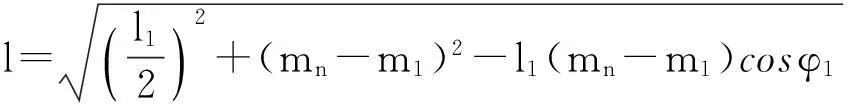
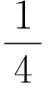

表2 每根木条开槽的长度
2.3 桌脚边缘线的数学描述
首先,可以写出桌面边缘线关于y的参数方程

由于将木条无限细化,可暂时忽略木板的厚度以及m1的大小,且钢筋位于最外侧木条的中心位置,因此可以获得钢筋最外侧的点的坐标方程如下
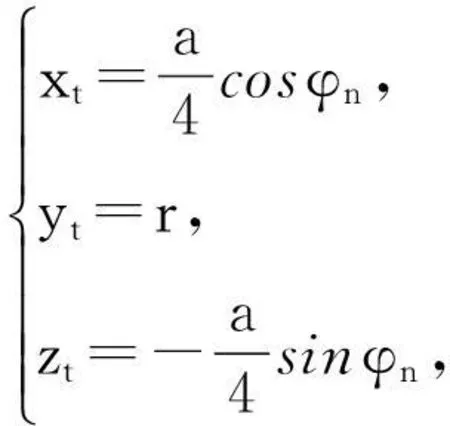
其中φn表示第n根木条与水平面的夹角.
桌子稳定放置在地面时,由于钢筋和地面平行,因此有

得
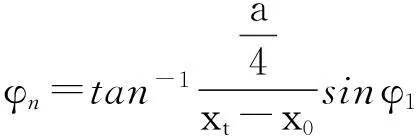
另外桌脚边缘线的坐标满足
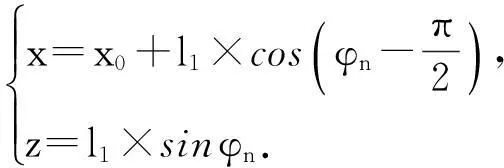
(1)
又由于l1和a之间存在如下关系
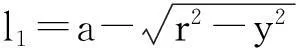
分别将l1,φn带入(1),由此可得到“桌角边缘线”关于y的参数方程:
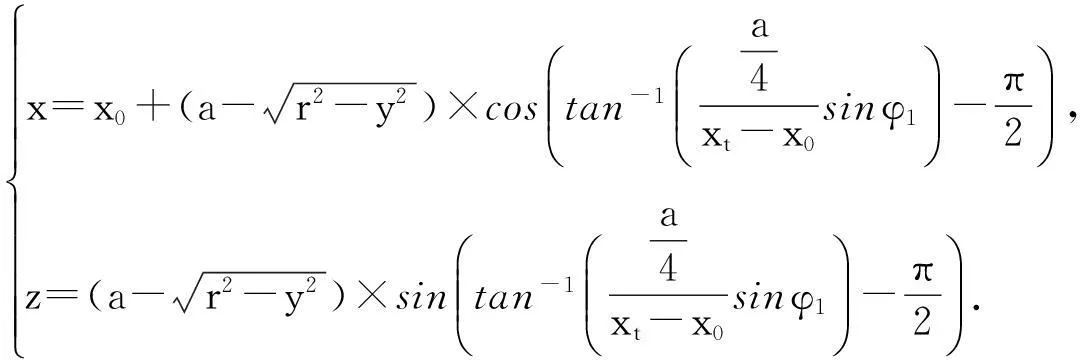
将n=1,…,10的情况分别算出10根木条的下端点的位置,描点连线得到桌脚边缘线的图像,如图7所示.
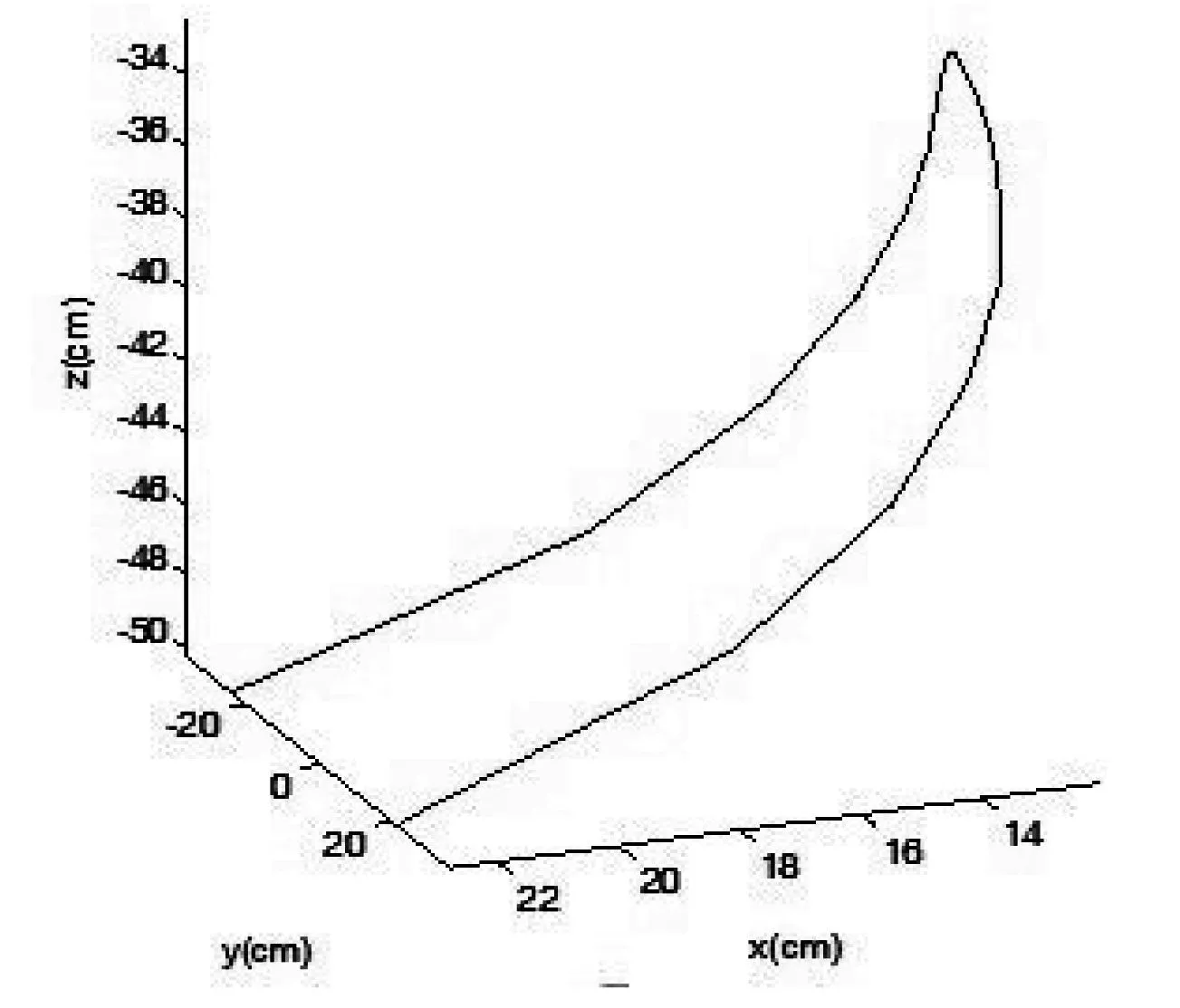
图7 桌面边缘线
3最优设计加工参数
当只给出折叠桌的高度和圆形桌面的直径来设计折叠桌,且使设计“稳固性好、加工方便、用材最少”.我们定义“稳固性好”为当桌面边缘放置重物时,桌面不会发生翻转,并且如果水平推拉桌子,桌子仍不会发生翻转或平移;定义“加工方便”为桌腿木条宽d越大(即个数越少、切割的次数越少)越方便;定义“用材最少”为木板本身的体积和开槽的总体积都尽可能小,则用材最少(考虑开槽的总体积是因为开槽的总体积表示浪费的木材,浪费的木材越多,用材越多).
此时桌子的设计与长方形平板材料(平板密度ρ,地面的摩擦因素μ及平板尺寸a×b×c)、折叠桌(桌腿条数N,钢筋位置p(钢筋距离最外侧木条顶端的距离)及开槽长度xn)这些设计加工参数相关.仍考虑平板为木板的情况,通常情况下,木板的密度ρ=0.6g/cm3,木板与地面的摩擦因素μ=0.4.
在考察稳固性、加工及用材之前,要使桌子能够设计出来,参数之间应首先满足一些限制条件.
(i) 钢筋的位置必定达到最短的桌腿木条顶端,否则不是所有的木条上都有钢筋,桌子会散架.如图8所示,即
p>mN-m1.
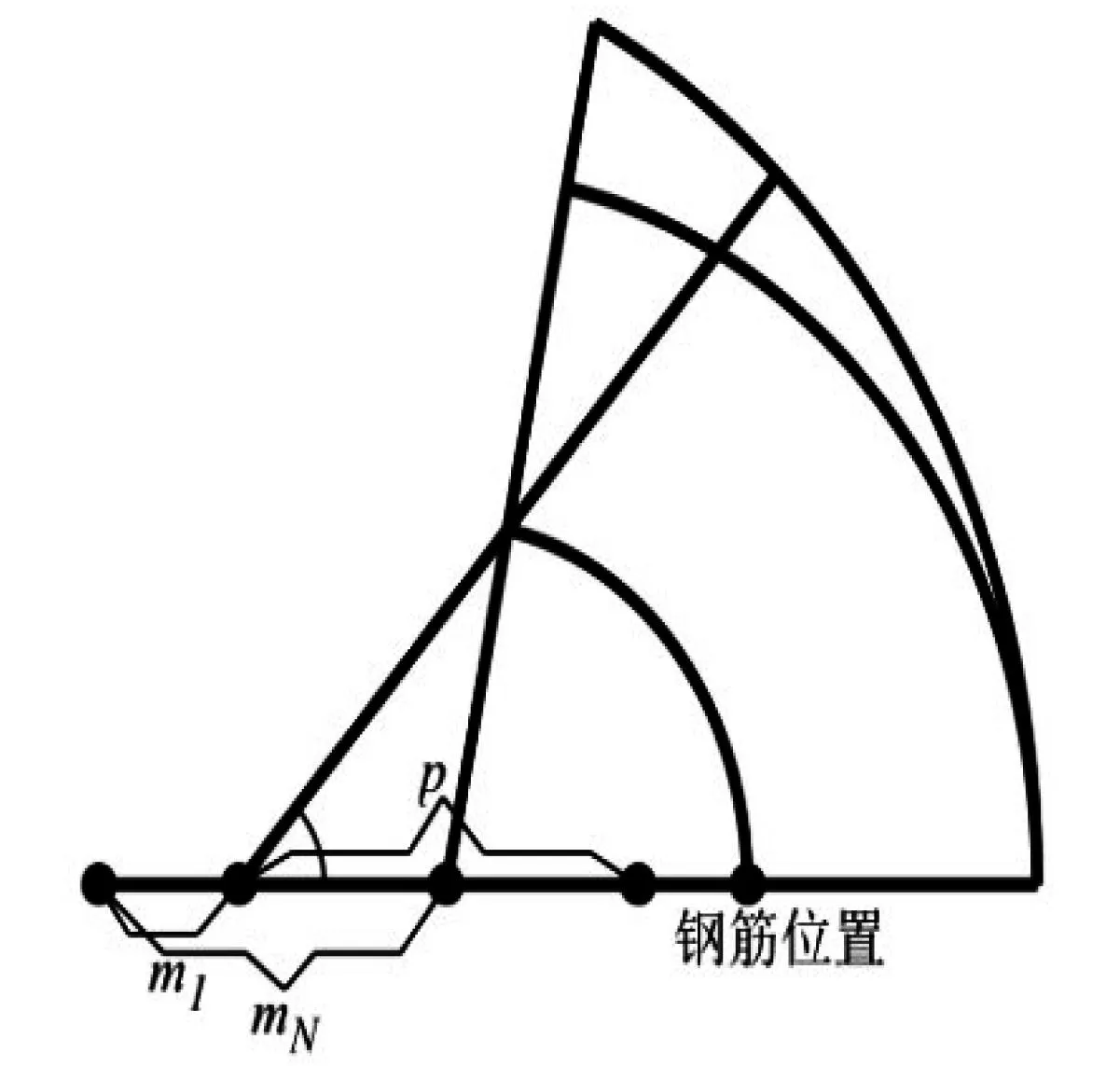
图8 平板桌侧视图
(ii) 折叠过程中钢筋一定不能超过木条的最低端.如图8所示,即
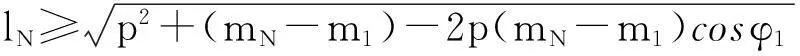
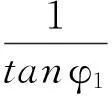
3.1 考察稳固性
根据定义分2种情况对桌子进行受力分析.一是在桌子边缘放置重物,使桌子不会发生翻转.由于圆形桌面上与木条相切的边无论怎样放置重物都不会造成桌子的翻转,故只考虑重物放置在桌面与x轴相交的最边缘点处.如桌子xOz平面截图图9所示:

图9 平板桌侧视图
翻转的情况只会发生在圆形桌面的半径超出支点,即r>d2的情况下.超出时,只有当重物放置的力F1小于重力mg对支点的力时,桌子才不会翻转,才稳固;在临界条件下,
F1d1=mgd2,
d1=r-l1cosφ1-m1d2=l1cosφ1+m1.
故重物放置的力F1的参数方程为
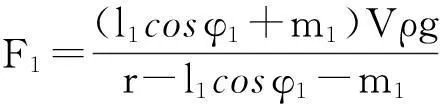
另一种情况是用水平的力去推桌子,当水平推力F2小于重力mg对支点的力,同时水平推力F2小于最大静摩擦力μmg时,桌子才既不会平移也不会发生翻转,所以F2要小于重力mg对支点的力和最大静摩擦力μmg的最小值,才稳固性好.临界条件下,
F2h=mgd2,F2=μmg,h=l1sinφ1.
故水平推力F2的参数方程为

3.2 考察加工方便性
桌腿木条的宽度表达式为

3.3 考察用材多少
因为长方形平板是规则的长方体,所以长方形平板的总体积
V=2(l1+m1)·c·2r,
(2)
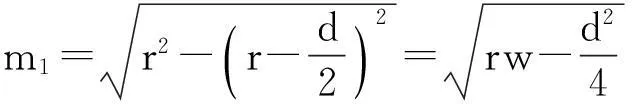
代入(2)得
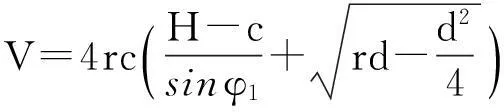
开槽的总长度

桌腿裁切后,桌面呈锯齿状而非纯圆形,为了使最终桌面的形状最大程度上近似于所要求设计的形状,故考察要求设计的圆形桌面的面积与裁切后锯齿状桌面的面积之差(裁切后锯齿状桌面的面积=整个长方形木板的面积减去总的裁切的桌腿木条的面积)
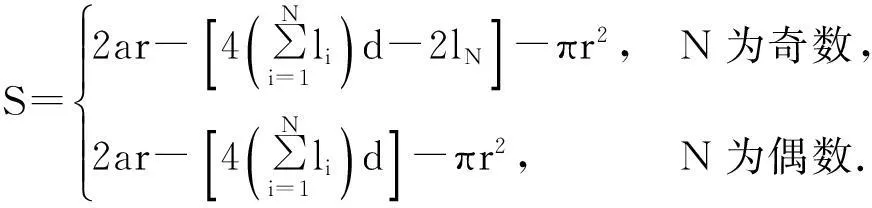
所以根据定义,要使稳固性好,重物放置的力F1和水平推力F2要越小越好.要做工方便,桌腿木条的宽度d要大(即条数、切割的次数少);要使用材最少,长方形平板的总体积V和开槽的总长度K要越小越好.圆形桌面的面积与裁切后桌面的面积之差S越小,越符合设计需求.所以要得出使折叠桌“稳固性好、加工方便、用材最少”的最优设计加工参数,即相当于求解一个有约束条件的非线性的多目标函数的优化问题[1-3],此时的目标函数为最大边界压力F1的负值、水平推力F2的负值、桌腿木条个数N、长方形平板总体积V、开槽总长度K和圆形桌面的面积与裁切后桌面的面积之差S这6个参数方程,且都求取其最小值.
将目标函数的6个方程,看成6个元素,共同构成一个6维的向量.因为6个函数均为连续函数,所以在选取领域解时,让其在规定范围内随机选取一个点作为该已知点的领域解.判断是否为最优解时,只有6维向量的每一个元素(即每一个目标函数)均小于当前解,选取的领域解才为新的最优解,可跳出.这属于“多目标模拟退火[4]”.同时本文采用SMOSA算法[5]决定跳出局部最优解的概率,则接受新解的概率为

本文采用模拟退火算法[6-7]求解设计模型的最优方案,得到最优设计加工参数为动态过程示意如图10:
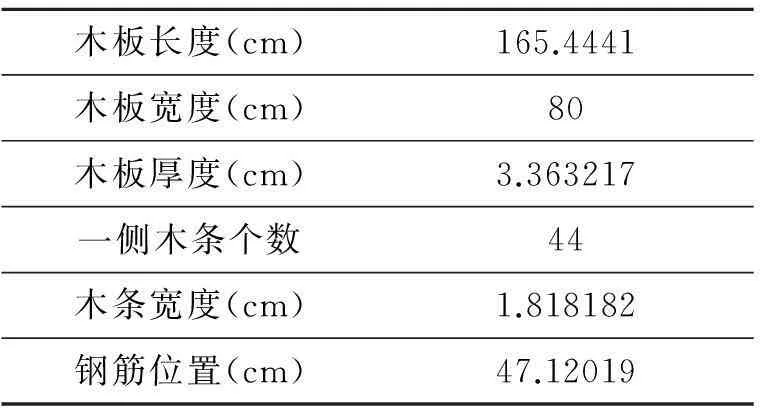
表3 最优设计加工参数

表4 开槽长度
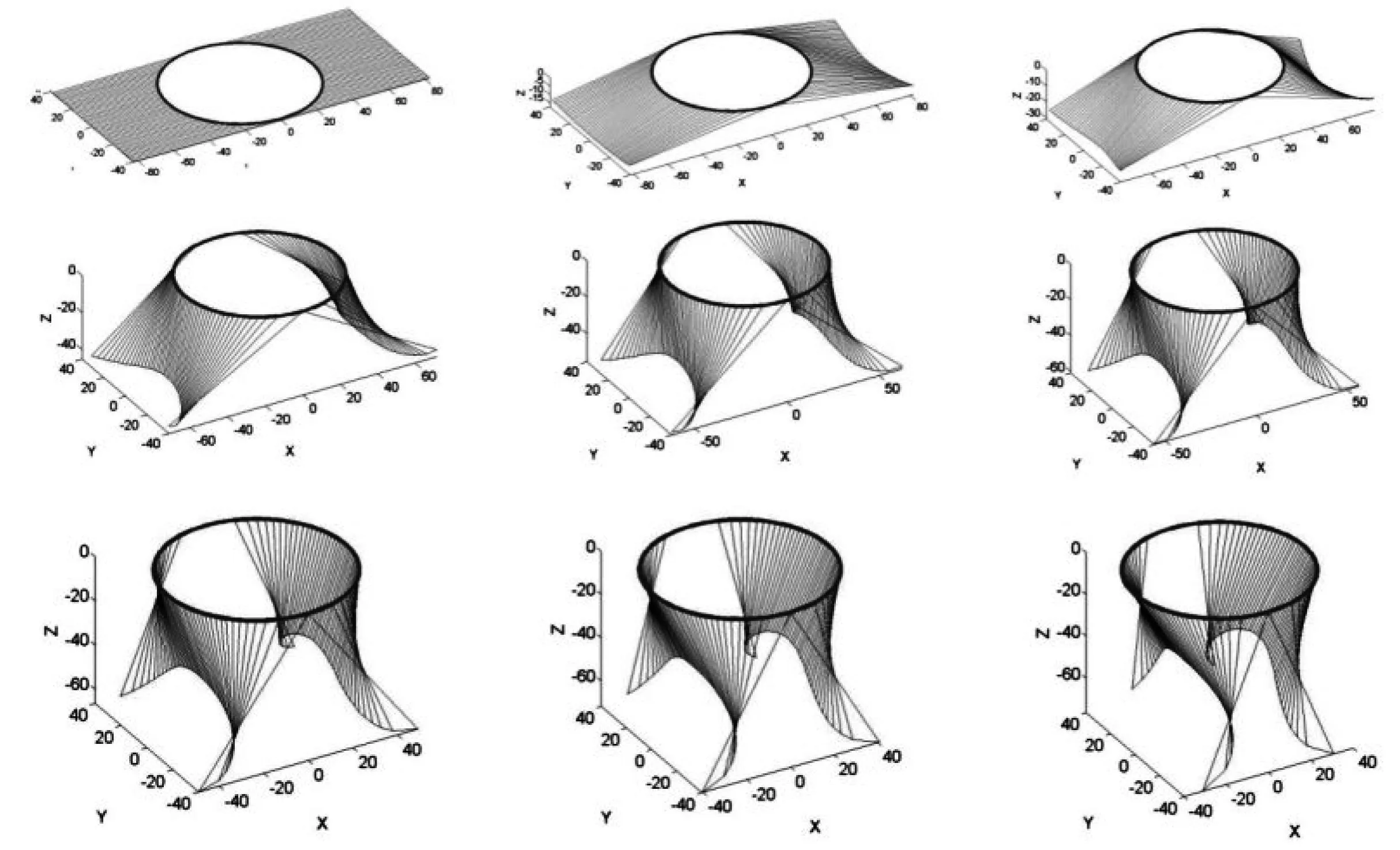
图10 动态变化过程图
4创意平板折叠桌最优设计模型
首先建立空间直角坐标系,根据客户给出桌面边缘线的形状,用一个参数方程表示这个平面上的曲线
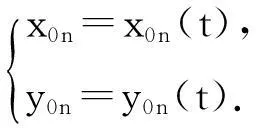
将切割方向旋转至与x轴平行的位置,桌面位于xOy平面,因此可以通过折叠桌的位置,用折叠桌的形状参数和位置参数来表示桌面边缘线上各点的坐标,即
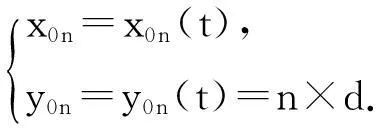
通过消参,可以得到一个含有变量t,n,d的方程,记作
H(t,n,d)=0.
(3)
其中t是桌面边缘线参数方程参变量,n表示第几个木条,d表示每个木条的宽度.
接着根据客户给出桌脚边缘线的形状,表示出其对应的方程.另外在同一y值下,桌面边缘线和桌脚边缘线上点的连线即为该处的木条.根据桌子在坐标轴的位置可以得到:
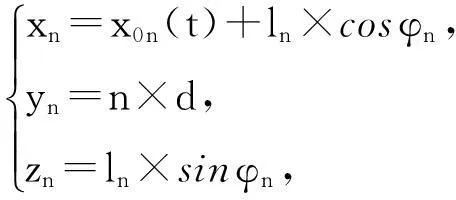
其中t是桌面边缘线参数方程参变量,n表示第几个木条,d表示每个木条的宽度,其中φn表示第n根木条与水平面的夹角,ln表示第n根木条的长度,(xn,yn,zn)表示桌脚边缘线的坐标.再将坐标带入客户给出的桌脚边缘线的方程,记作

(4)
通过最优设计加工参数的分析有
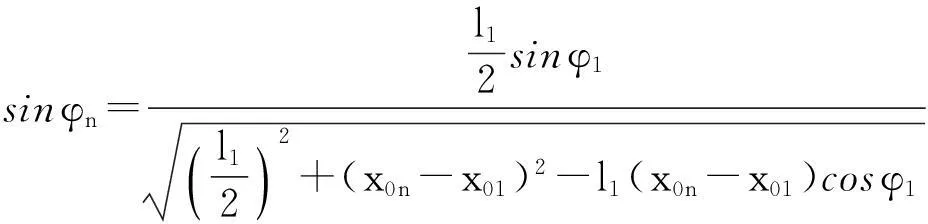
其中φ1表示第1根木条与水平面的夹角.不妨记作
sinφn=G(φ1,l1,x0n,x01).
通过最优设计加工参数的分析有
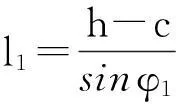
不妨记作
l1=R(h,c,φ1).
将l1带入sinφn可得
φn=G(φ1,l1,x0n,x01).
通过最优设计加工参数的分析有
l=l1+x01(t)=ln+x0n(t)=R(h,c,φ1)+x01(t).
因此
ln=R(h,c,φ1)+x01(t)-x0n(t).
将φn和ln代入(4)有
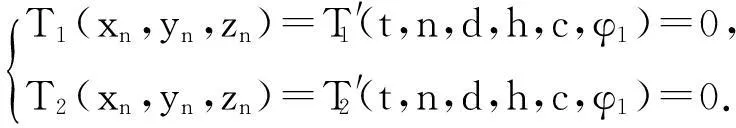
(5)
再将(5)和(3)联立消去参变量n得到方程记作
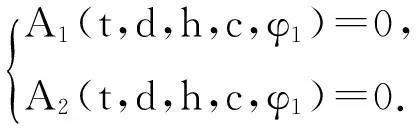
该式中h为客户设定的桌面高度,因此可以得到t,d,h,c,φ1的限制条件.
接下来仍用模拟退火[6-7]的方法,运用最优设计加工参数中的六个目标函数的表达方式来选取最优解,其中h由顾客提供,所以目标函数[5]如下:

约束条件为
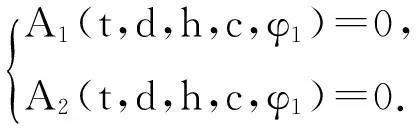

表5 每根木条开槽的长度
若桌面为三角形,平板尺寸为160cm×50cm×3cm,钢筋位置p=60cm.

表6 每根木条开槽的长度
其动态变化过程的示意图为
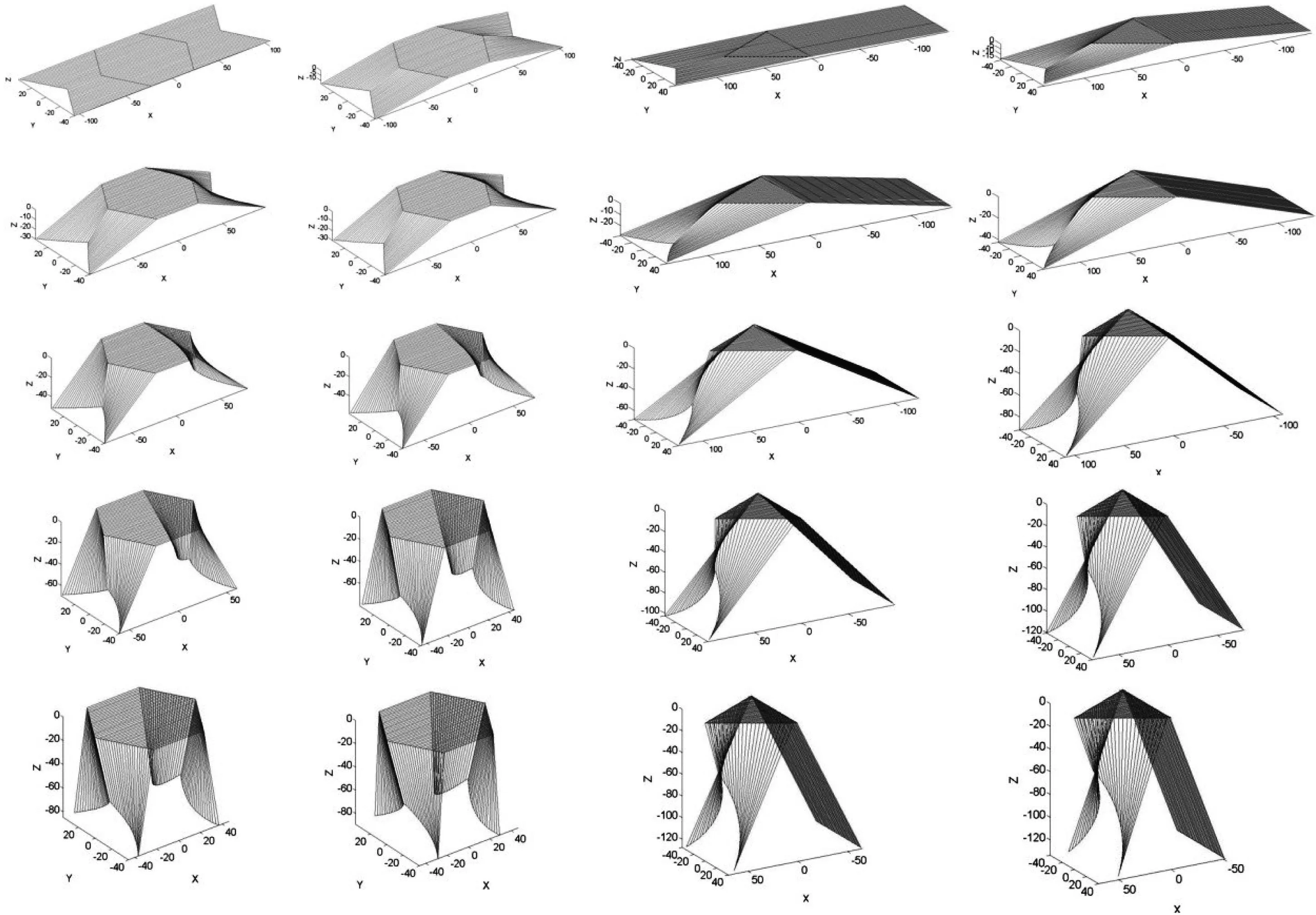
图11 六边形和三角形平板桌动态图
5模型总结及改进
本文先考虑了桌高、平板尺寸和形状、桌面尺寸和形状、木条宽度及钢筋位置都确定的情况.通过分析,建立了初等函数模型,得到折叠桌桌面的参数方程和木条顶点坐标.通过描述木条下端点的变化轨迹,给出折叠桌的动态变化过程.在此基础上分析了平板折叠前、后的几何关系,得到木条的开槽长度.最后将木条细化,通过每根木条的下端点坐标,得到桌脚边缘线的函数表达式.
当只给定桌高和桌面直径时,根据设计上“稳固性好、加工方便、用材最少”的要求,得出最大边界压力、最大水平推力、木条宽度、平板体积、开槽总长度、预想面积与实际面积之差的6个目标函数.本文采取了基于多目标函数的“模拟退火”算法,通过SMOSA算法决定跳出局部最优解的概率,从而求取出使该带有约束条件的非线性多目标函数规划问题达到最优值的设计加工参数.
对于客户任意给定的创意折叠桌,我们可通过顾客给出的桌面和桌脚边缘线的形状得到它们的曲线方程,用折叠桌的形状参数和位置参数来表示桌面边缘线上各点的坐标.,进而得到桌脚边缘线的参数方程,再将其转化为用折叠桌的形状参数和位置参数表示的曲线方程.将有关折叠桌形状参数和位置参数的桌面、桌脚边缘线的参数方程联立,得到折叠桌加工参数的限制条件.最后在限定条件下运用模拟退火算法得到最优解.
对于折叠桌最优设计的确定,可请客户明确给出考察“稳固性好、加工方便、用材最少”的重要性排序,我们可根据重要性给出权重,采取给各个目标函数赋权的方法,确定最优设计加工参数,而不是如本文所述,在模拟退火中,6维元素的初始温度和下降系数都相同,这样可使折叠桌的设计更加符合客户的需求.
注本文获得2014年高教社杯全国大学生数学建模竞赛全国一等奖.指导教师:北京师范大学数学科学学院王颖喆
[参考文献]
[1]刘淳安.动态多目标优化进化算法及性能分析[J].计算机仿真,2010,27(4):201-205.
[2]雷德明,严新平.多目标智能优化算法及其应用[M].北京:科学出版社,2009.
[3]刘鹏飞,董守斌,曹以诚,等.多目标优化的非编码RNA比对及预测[J].计算机工程,2009,35(9):225-226.
[4]张长林,余建星,杨振国.非线性约束最优化问题的多目标模拟退火算法[J].复旦学报(自然科学版),2003,42(1):93-97.
[5]李金忠,夏洁武,曾小荟,曾劲涛,刘新明,冷明,孙凌宇.多目标模拟退火算法及其应用研究进展[J].计算机工程与科学,2013,35(8):77-88.
[6]王爱莲.基于模拟退火算法的函数极值分析[J].电脑开发与应用,2009,22(10):13-14.
[7]胡大伟,朱志强,胡勇.车辆路径问题的模拟退火算法[J].中国公路学报,2006,19(4):123-126.
A Study on Optimal Design of Flat Folding Table
ZHANGXue-lei1,WANGJia-ying1,WULei2
(1. Beijing Normal University, School of Methematical Science, Beijing 100875, China;
2. Beijing Normal University, School of Information Science and Technology, Beijing 100875, China)
Abstract:There is a creative flat folding table.We build an elementary function model to give the dynamic change process of the table and functional expressions of the length of slots and the edge lines of legs of the desk.According to the stability,the difficulty of process and the quantity of material,we build a multi-objectives functional optimization model,and seek optimal design with simulated annealing algorithm based on multi-objectives function.At last,an elementary objective function model of the flat folding table is given.And then we design two new creative flat folding table by the model.
Key words:flat folding table; dynamic change process; the parameters of design; optimization; nonlinearmulti-objectives programming with constraints; simulated annealing
[中图分类号]O224
[文献标识码]B
[文章编号]1672-1454(2015)05-0023-10
[收稿日期]2015-06-16
