非齐次树上连续马氏信源的若干强偏差定理
2016-01-28陈秀引金少华刘伟娜
陈秀引, 王 东, 金少华, 刘伟娜
(1.河北工业大学理学院,天津300401; 2.河北工业大学廊坊分校,河北廊坊065000)
非齐次树上连续马氏信源的若干强偏差定理
陈秀引1,王东2,金少华1,刘伟娜1
(1.河北工业大学理学院,天津300401;2.河北工业大学廊坊分校,河北廊坊065000)
[摘要]通过构造适当的非负鞅,将Doob 鞅收敛定理应用于几乎处处收敛的研究,研究给出了一类非齐次树上r重连续马氏信源熵密度的若干强偏差定理.
[关键词]非齐次树; 鞅; 马氏信源; 强偏差定理
1引言
树指标随机过程已成为近年来发展起来的概率论的研究方向之一.强偏差定理一直是国际概率论界研究的中心课题之一.文献[1] 研究给出了Bethe树上非齐次马尔科夫随机场的一类强偏差定理.本文通过构造适当的非负鞅,将Doob 鞅收敛定理应用于几乎处处收敛的研究, 研究给出了一类非齐次树上r重连续马氏信源熵密度的若干强偏差定理.
2定义
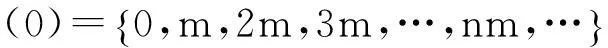

……………………………
(m-1)={m-1,2m-1,3m-1,…,(n+1)m-1,…}.
当n∈(i)时,令Nn+1=αi(αi均为正整数且不同时为1),i=0,1,2,…,m-1, 就得到了一类特殊的非齐次树Tα0,α1,…,αm-1. 以下恒以T表示树Tα0,α1,…,αm-1.
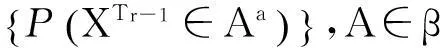
(1)

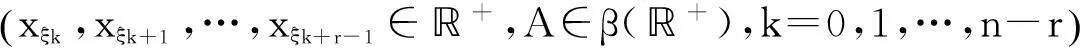
(2)
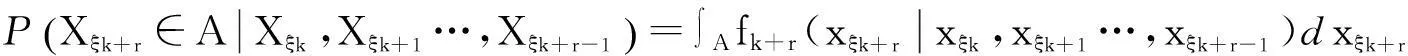
(3)
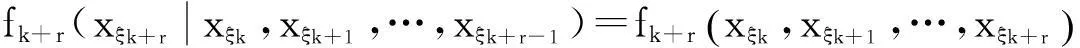
则
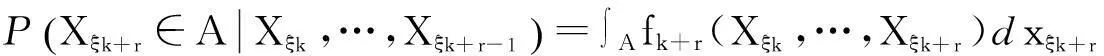
(4)
且上述树T上的非齐次马氏信源的联合密度函数为
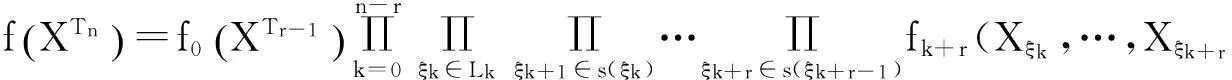
(5)

(6)
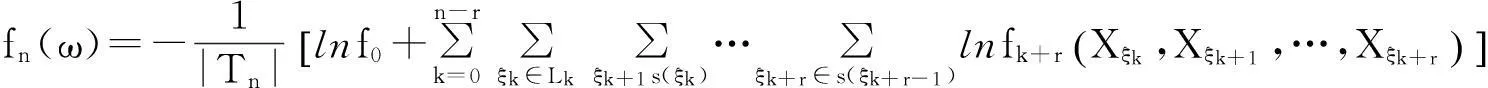
(7)
本文引入如下似然比
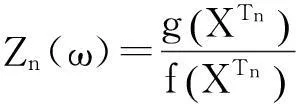
(8)
和对数似然比
φn(ω)=lnZn(ω).
(9)
令

(10)
定义2.2设λ为一实数,对任意的
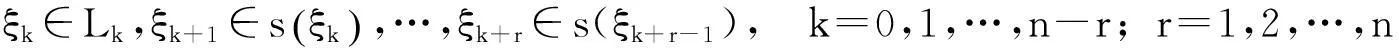
称

(11)
为函数-lnfk+r(Xξk,…,Xξk+r)的Laplace变换.
3主要结果及其证明

(12)

(13)
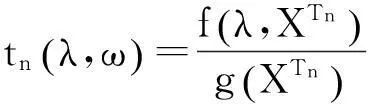
(14)
证由(6)式,有
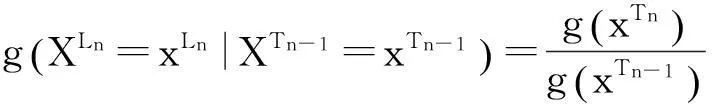
(15)
由(12)式、(13)式和(14)式有
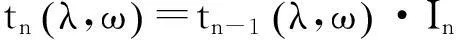
(16)
其中
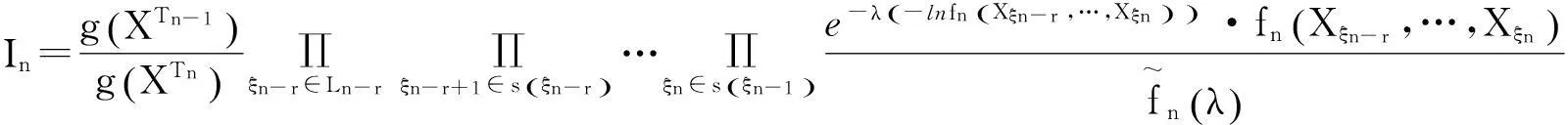
(17)
而
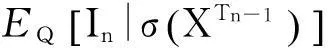
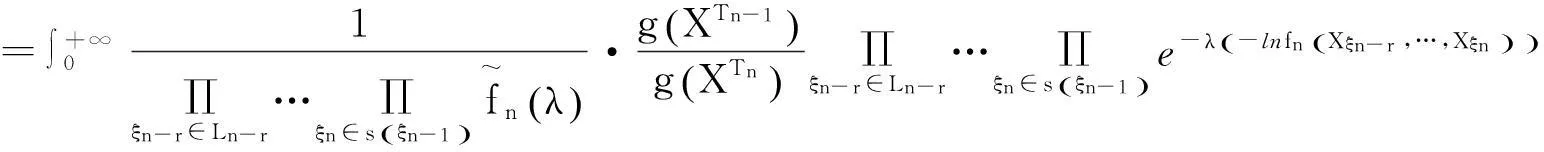


=1.
(18)
从而由(16)式和(18)式,有
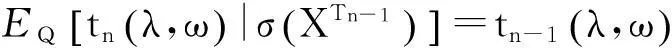

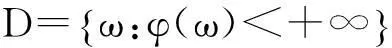
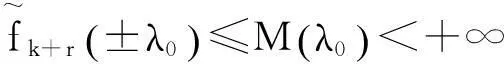
(19)
则


(20)
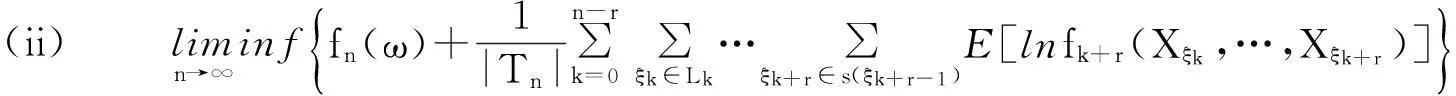

(21)
其中
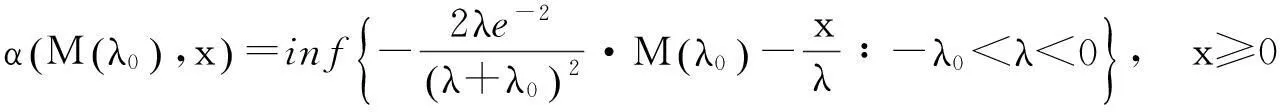
(22)
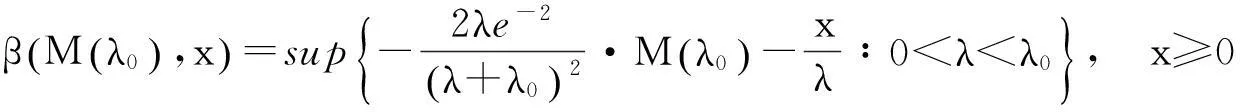
(23)
并且
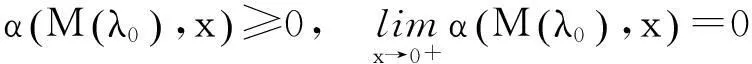
(24)
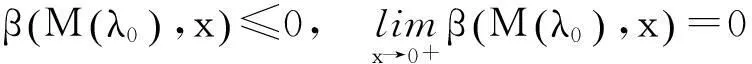
(25)

(26)
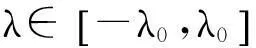
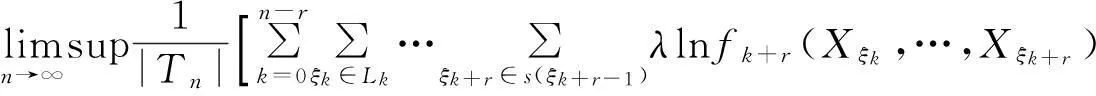
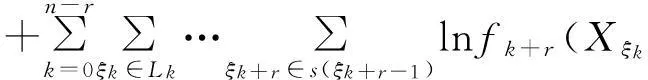

(27)
由上极限的性质和(27)式,有
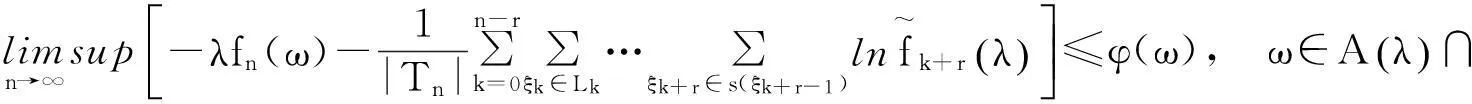
(28)
在(28)中取λ=0,有
φ(ω)≥0,ω∈A(0)∩D.
(29)
(i) 当-λ0<λ<0时,将(28)式两端同除以-λ,有

(30)
由上极限的性质及不等式lnx≤x-1(x>0),有
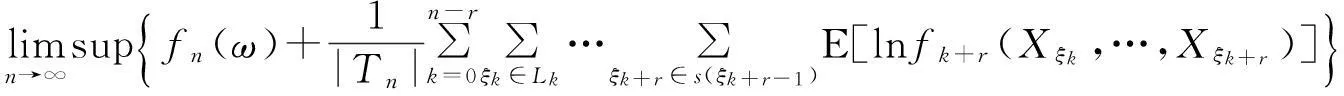
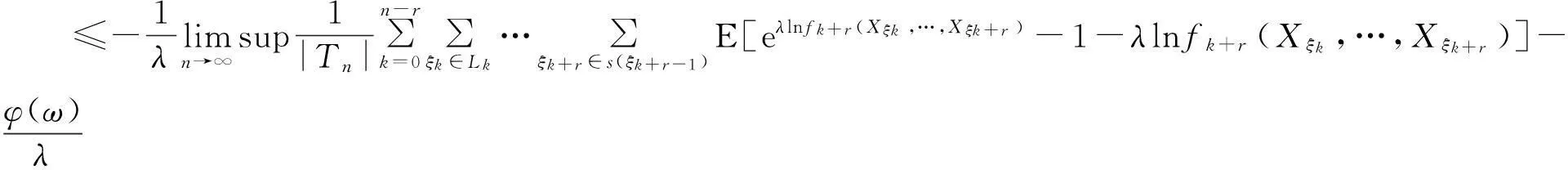
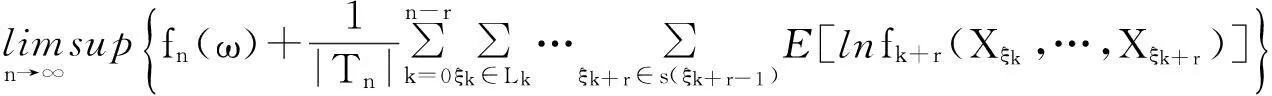
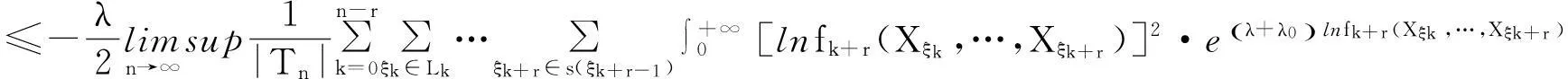

(32)
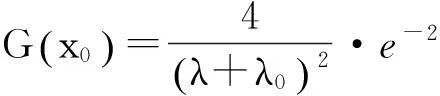
(33)

(34)
由(32)式及(34)式,有
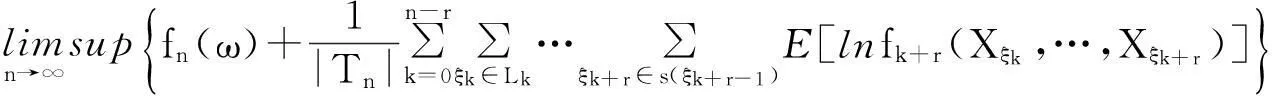
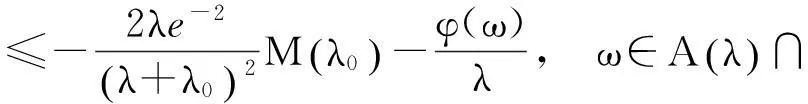
(35)
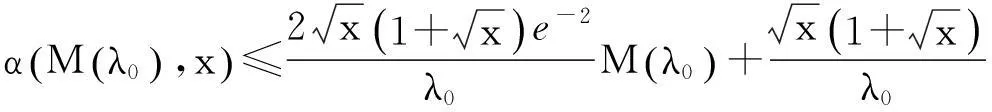
(36)
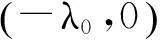
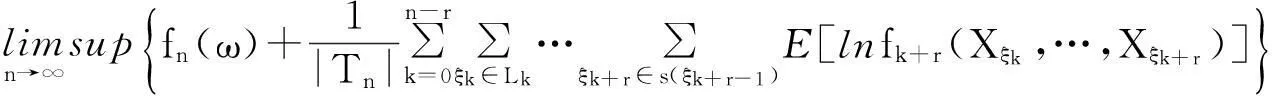
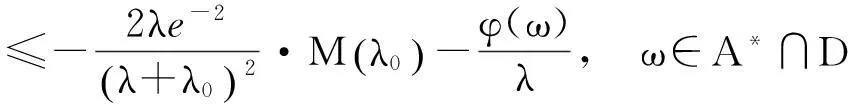
(37)
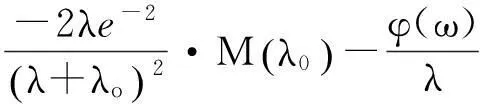
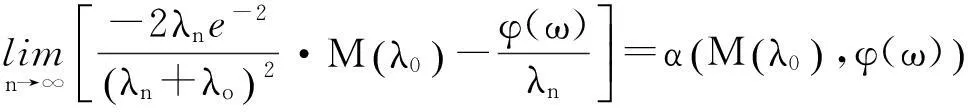
(38)
由(37)式,有
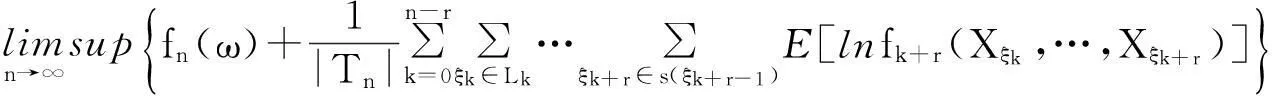

(39)
由(38)式和(39)式,有
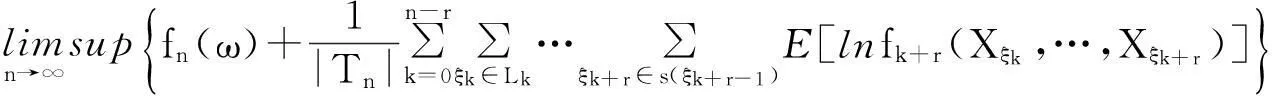

(40)
(ii) 证明类似于(i)的证明.
[参考文献]
[1]Yang W G.. A class of deviation theorems for the random fields associated with non-homogeneous Markov chains indexed by a Bethe tree, Stochastic Analysis and Applications, 2012, 30(2):220-237.
A Class of Strong Deviation Theorems of Continuous Markov Information
Source on a Non-homogenous Tree
CHENXiu-yin1,WANGDong2,JINShao-hua1,LIUWei-na1
(1. College of Science, Hebei University of Technology, Tianjin 300401,China;
2. Langfang Branch, Hebei University of Technology, Langfang 065000,China)
Abstract:Through constructing a non-negative martingale and applies Doob's martingale convergence theorem to the research of a.e. convergence, a class of strong deviation theorems of the entropy density of r-ordered continuous Markov information source on a non-homogenous tree are given.
Key words:non-homogeneous tree ; martingale ; Markov information source ; strong deviation theorem
[中图分类号]O177.91
[文献标识码]A
[文章编号]1672-1454(2015)05-0001-05
[基金项目]河北省高等学校科学技术研究重点项目(ZD2014051)
[收稿日期]2015-07-19
