液压机械无级变速器机械变速机构的传动误差分析

雷贤卿　蔡振华　张明柱　马文锁

河南科技大学,洛阳,471003



液压机械无级变速器机械变速机构的传动误差分析

雷贤卿蔡振华张明柱马文锁

河南科技大学,洛阳,471003

摘要：以东方红某型号拖拉机液压机械无级变速器中的机械变速机构为研究对象，探究其传动误差随时间的变化规律，目的是减少变速器的功率损耗。利用当量啮合误差原理，建立变速器中行星齿轮组、定轴齿轮副和两者共同作用时的传动误差与时间的关系式。比较各挡位的总传动误差和行星齿轮组传动误差，得到瞬时总传动误差最大、最小的挡位以及总传动误差的主导因素。在角频率相同时，行星齿轮组传动误差和定轴齿轮副传动误差存在耦合关系。利用蒙特卡罗法，验证了研究所得规律的正确性。建立总传动误差与功率损耗的关系式，结果表明两者存在正比关系。以减小传动误差为目的，提出了减少变速器功率损耗的措施。

关键词：拖拉机；液压机械无级变速器；传动误差；蒙特卡罗法；功率损耗

0引言

液压机械无级变速器(HMCVT)中的机械变速机构主要由行星齿轮组和定轴齿轮副组成，它具有输出功率大、传动效率高等优点，已被广泛应用于拖拉机中[1]。如果HMCVT存在传动误差，则会引起其功率损耗，影响拖拉机的使用性能。因此，研究HMCVT的传动误差具有重要的工程实用价值。

国内外学者主要从静态和动态两个方面对各类齿轮传动机构的传动误差进行研究。静态上，主要以建立静态特性下行星齿轮传动误差的等价模型为方法，以提高行星齿轮的传动精度为目的，对各类行星齿轮的传动误差进行研究[2-10]，但缺乏对行星齿轮机构动态传动误差的研究，缺少对行星齿轮组和定轴齿轮副共同工作时总传动误差的研究。动态上，主要基于蒙特卡罗思想，对行星齿轮传动误差的随机变量进行抽样，从而找到传动误差的分布情况[11-12]，缺乏对行星齿轮传动误差随时间变化规律的研究。

本文以东方红某型号变速器为研究对象，依照拖拉机功率大、转速低、扭矩大[13]的特点，建立HMCVT机械变速机构中行星齿轮组、定轴齿轮副和两者共同作用时的传动误差与时间的关系式。探究总传动误差和行星齿轮组传动误差随时间的变化规律。基于蒙特卡罗思想，验证研究所得规律的正确性。探究功率损耗与传动误差的关系，以减小传动误差为目的，提出减少变速器功率损耗的措施。

1传动误差影响因素

1.1齿轮制造误差

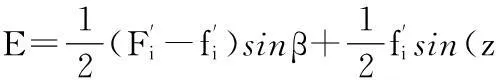
(1)

式中，β为制造误差的相位角；z为齿数。

(2)

式中，ω′为齿轮的角频率；t为时间；φ′为制造误差的初相。

1.2齿轮安装误差

齿轮安装误差A由齿轮孔之间的间隙e1、齿轮安装处轴颈跳动间隙e2、轴承的径向间隙e3组成。综合考虑上述三种误差因素，安装误差的计算式为[12]

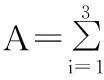
(3)

式中，ei为各跳动量；γi为各跳动量的相位角。

ei是随机变量，满足正态分布；γi是随机变量，满足[0,2π]间的均匀分布，建立安装误差与时间的关系式：

(4)

式中，ω″i为各跳动量的角频率；φ″i为各跳动量的初相。

单个齿轮的综合误差T由E和A组成[12]:

T=E+A

(5)

1.3当量啮合误差

行星齿轮传动误差的影响因素除了有太阳轮s、行星轮pi、行星架c、内齿圈I和轴承b的制造误差和安装误差，还有由制造、安装误差引起的当量啮合误差。当量啮合误差是将构件的制造误差和安装误差折算到齿轮内外啮合线上的等效误差[11]，用e表示。β、ω为行星齿轮各部件的相位角、角频率；αn、αw表示内外啮合线上的啮合角；φi为第i个行星轮相对于第一个行星轮的位置角。太阳轮的制造误差Es、太阳轮的安装误差As、太阳轮轴承的制造误差Ebs、行星轮的制造误差Epi、行星轮的安装误差Api、行星轮轴承的制造误差Ebpi、行星架的制造误差Ec、内齿圈的制造误差EI、内齿圈的安装误差AI所引起的内外啮合线上的当量啮合误差见表1[11]。

表1　各类误差项引起的当量啮合误差

可得各类误差项在内外啮合线上引起的当量啮合误差分别为[11]

en=eEIi+eAIi+eEpiI+eApiI+eEbpiI+eEcIi

(6)

ew=eEsi+eAsi+eEbsi+eEspi+eAspi+eEbspi+eEcsi

(7)

2传动误差的计算

2.1计算关系式

齿轮的传动误差为实际转角与理论转角之差，得到的值为正值说明实际转角比理论转角大，反之则正好相反。规定逆时针为齿轮转动正方向，顺时针为反方向。一对定轴齿轮副的传动误差的计算式为

(8)

式中，r2为分度圆半径；θ为定轴齿轮副传动误差。

行星齿轮传动时如果内齿圈为输入端，内外啮合线的当量啮合误差造成的内齿圈的传动误差分别为

(9)

(10)

式中，rb为基圆半径；i为传动比；Δθ为行星齿轮传动误差。

则内齿圈转角误差为

(11)

内齿圈与行星架相对传动误差为

(12)

通过以上分析，可得行星齿轮各部件之间任一部件的传动误差，也可得以任一部件作为输入端，其余任一部件作为输出端的传动误差。行星齿轮中各部件的制造误差和安装误差可由式(2)和式(4)求得。以太阳轮的制造误差为例，太阳轮的制造误差和安装误差引起的当量啮合误差分别为

sin[(ωs-ωc)t+βs+αw-φi]

(13)

(14)

行星齿轮组输出端传动误差作为定轴齿轮副输入端传动误差，总传动误差为

φ=Δθ+θ

(15)

2.2计算模型

变速器传动原理图见图1，其中，Ⅰ轴为输入轴；Ⅵ为输出轴；液压马达与行星排K1、K2的太阳轮连接。输入轴驱动K1的齿圈和K2的行星架，离合器Cf、Cr分别在前进和倒车时接合。各挡位的离合器结合状态见表2，“+”、“-”分别表示离合器接合、分离，H、HM分别表示纯液压挡、液压机械挡。p11表示行星排K1的第一个行星轮，依此类推。离合器C1控制定轴齿轮副z1、z2；离合器C2控制定轴齿轮副z3、z4；离合器C3控制定轴齿轮副z5、z6；离合器C4控制定轴齿轮副z7、z8；离合器Cf控制定轴齿轮副z9、z10；离合器Cr控制定轴齿轮副z11、z12。

图1　变速器传动原理图

方向挡位CyC1C2C3C4CfCr前进H1+----+-HM2-+---+-HM3--+--+-HM4---+-+-HM5----++-后退H1+-----+HM2-+----+HM3--+---+HM4---+--+HM5----+-+

东方红某型号HMCVT中机械变速机构的各项参数见文献[14]。K1、K2都以各自的行星架为安装基准，即行星架的安装误差为零。K1、K2的行星架制造误差为12 μm、10 μm。根据各齿轮尺寸和精度等级，参考GBl0095-88可得各部件的误差参数，如表3所示。

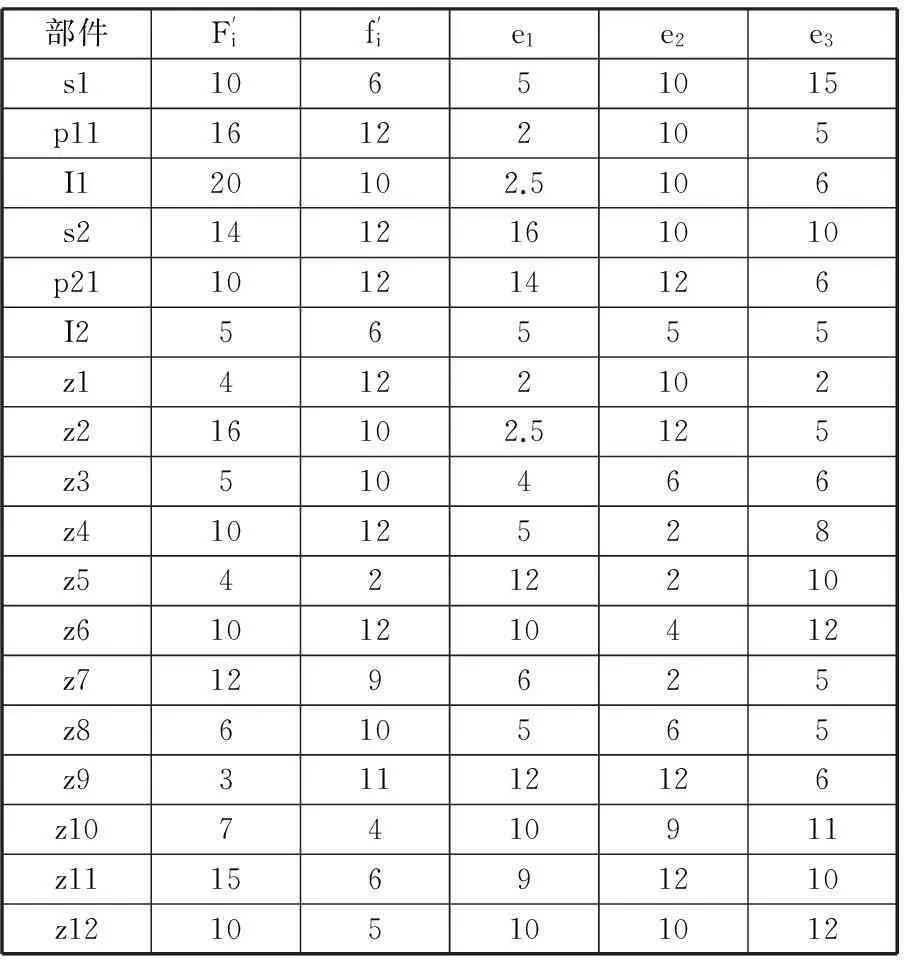
表3　各部件的误差参数　μm

由表3可以看出，齿轮制造误差的影响因素以及安装误差的影响因素没有规律性，在计算制造误差和安装误差时，需依照具体情况分析，综合考虑各种误差影响因素，从而得出系统总传动误差。

3传动误差的变化规律

前进挡HM2时，功率由C2输入，依次经过I1、p1、C1、z1、z2、z9、z10，从Ⅵ轴输出；前进挡HM3时，功率由C2输入，依次经过p2、I2、z3、z4、z9、z10，从Ⅵ轴输出；前进挡HM4时，功率由C2输入，依次经过I1、p1、C1、z5、z6、z9、z10，从Ⅵ轴输出；前进挡HM5时，功率由C2输入，依次经过p2、I2、z7、z8、z9、z10，从Ⅵ轴输出；后退挡HM2时，功率由C2输入，依次经过I1、p1、C1、z1、z2、z11、z12，从Ⅵ轴输出。可得各挡位的行星齿轮组传动误差Δθ、总传动误差φ的变化规律，如图2所示。

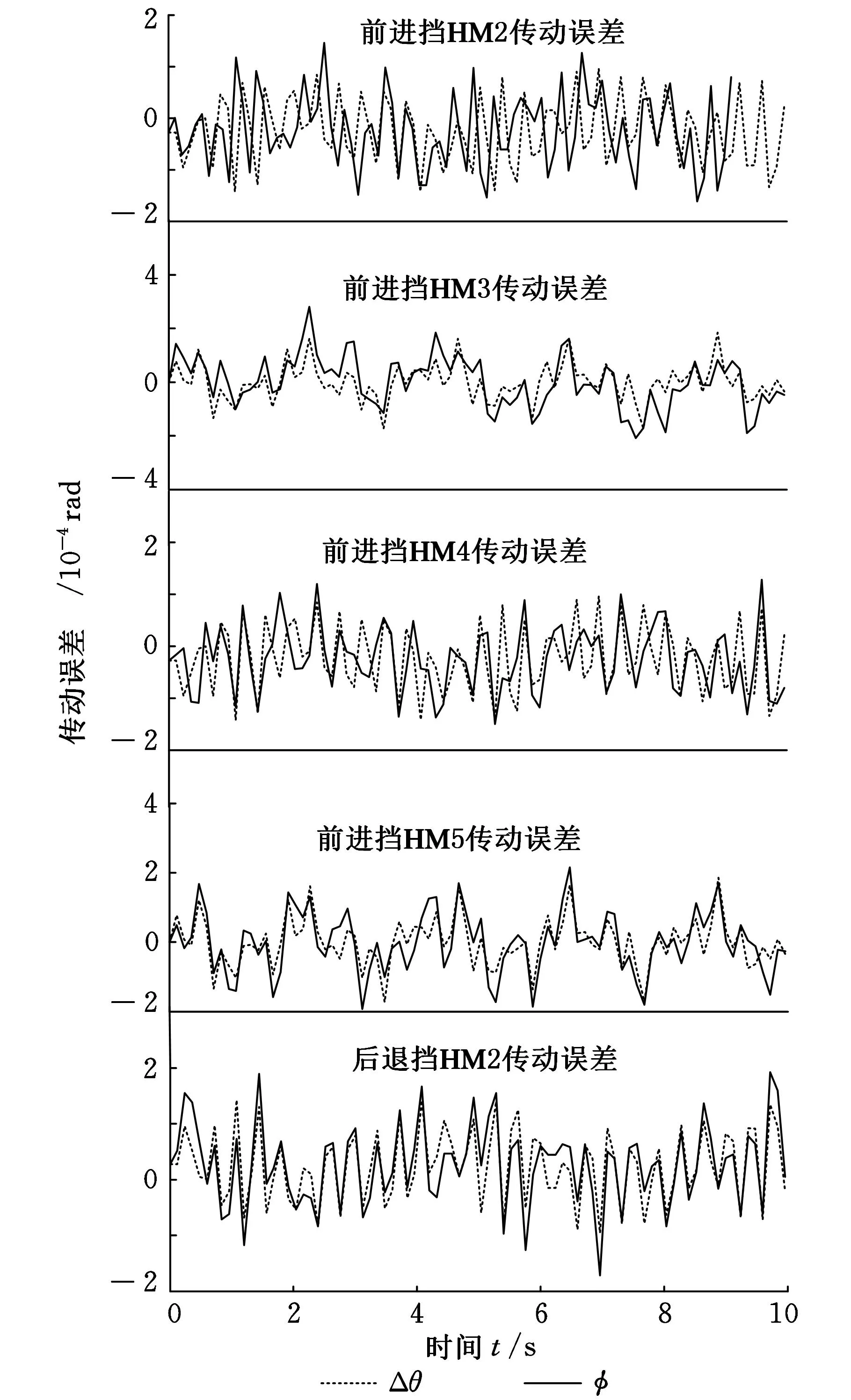
图2　各挡位的传动误差变化规律

由图2可得如下几点：

(1)正向时，HM3的瞬时总传动误差最大，为2.808×10-4rad，即57.92″，HM4的瞬时总传动误差最小，为1.281×10-4rad，即26.42″，前者是后者的219%；反向时，HM3的瞬时总传动误差最大，为2.082×10-4rad，即42.94″，HM4的瞬时总传动误差最小，为1.498×10-4rad，即30.89″，前者是后者的139%。

(2)行星齿轮和定轴齿轮副在传动过程中会出现角频率相同的情况。如HM2挡，K1的行星架的制造误差与z1的安装误差的角频率相同。此时两误差之间有耦合作用，耦合误差周期为2π，在0或2π处叠加关系最强，耦合误差最大，在π处两者抵消最明显，耦合误差最小。依此类推，在n(n取任意正整数)个周期处耦合误差最大，导致总传动误差大于行星齿轮组传动误差，耦合误差的大小由各误差分量的误差值决定。在n/2(n取任意正奇数)个周期处耦合误差最小，导致总传动误差小于行星齿轮组传动误差，各误差分量的初始相位之差决定了误差分量之间的抵消程度。

(3)比较各挡位总传动误差和行星齿轮组传动误差的峰值，可知两者相差不大，以HM2在1.56 s时为例，行星齿轮组的传动误差约占总传动误差的66.5%，可知总传动误差的主导因素是行星齿轮组传动误差。

(4)比较前进挡HM2和后退挡HM2的传动误差，在时间相同时，两者的传动误差大小相等方向相反，变化规律相同。由于后退挡与前进挡相比，只是在Cf处实现反转，由此可推知，其他各后退挡的传动误差均与相应前进挡的传动误差大小相等方向相反，满足前进挡的一切规律性。

4传动误差的蒙特卡罗法分析

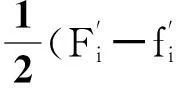
(16)

(17)

式中 ，R为服从[0,1]均匀分布的随机变量 ；η为分布参数；X为随机变量。

(18)

(19)

制造误差β和安装误差各跳动量γi的相位角均满足[0,2π]间的均匀分布，则抽样公式为

X=2πR

(20)

安装误差的各间隙ei满足正态分布，其抽样公式、分布参数分别为

(21)

μi=σi=ei/6

(22)

式中， μ为期望；σ为标准差。

行星齿轮组中以eEIi为例，可得βI满足[0,2π]间的均匀分布，概率密度为

f(βI)=1/2π0≤βI≤2π

(23)

EI满足瑞利分布，概率密度为

(24)

式中，q为出现在公差范围外的概率。

蒙特卡罗法计算步骤如下：

(1)根据式(18)、式(19)、式(22)、式(24)求出各误差参数；

(2)产生服从[0,1]均匀分布的随机数，根据式(17)、式(20)、式(21)、式(23)抽样得出抽样值；

(3)依照步骤(1)、步骤(2)的方法得到其余当量啮合误差的参数；

(4)根据式(9)到式(12)得到行星齿轮组传动误差，根据式(8)得到定轴齿轮副的传动误差，根据式(15)得到总传动误差；

(5)重复步骤(2)~步骤(4)50 000次，误差初相取任意值，每次取总传动误差绝对值进行统计分析，画出直方图。

后退挡总传动误差和前进挡总传动误差取绝对值后，大小、方向均相同，直方图完全一致，可得各挡位的总传动误差直方图，见图3。

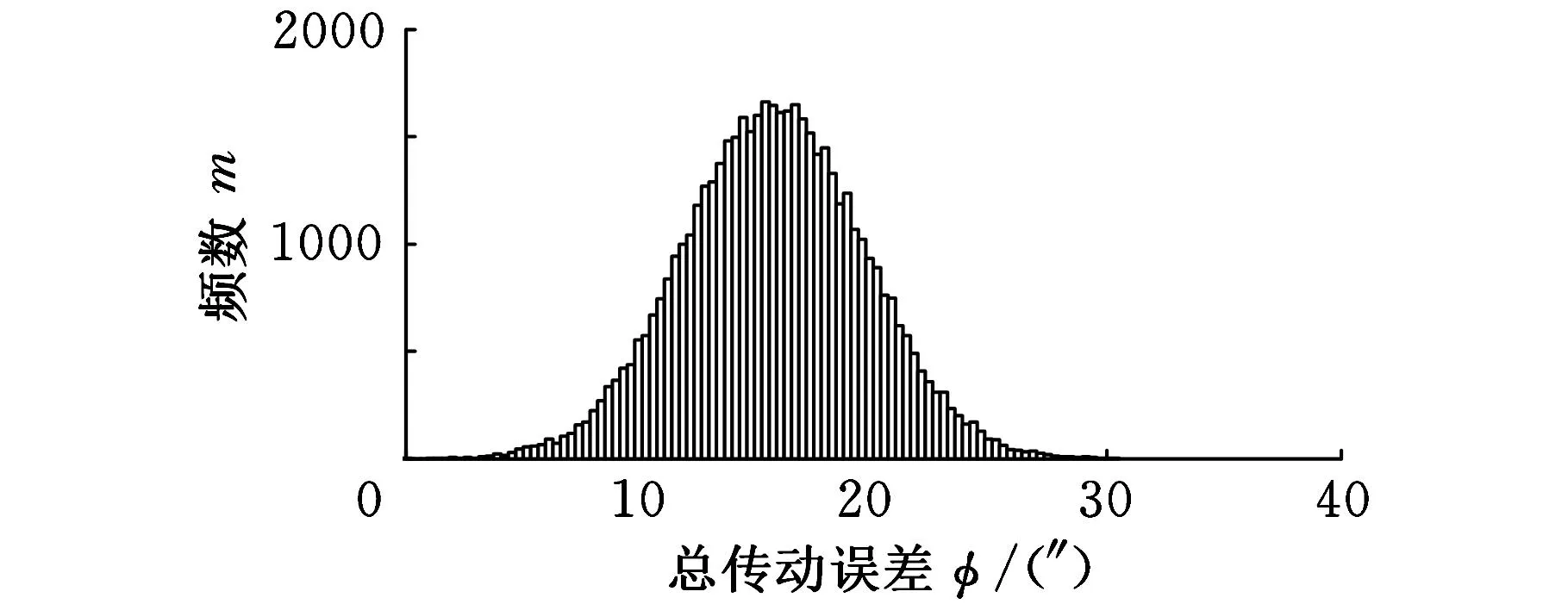
(a)HM2总传动误差直方图

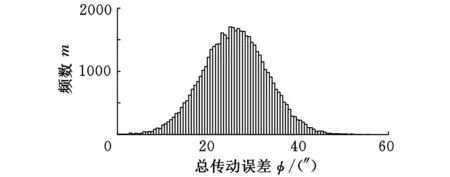
(b)HM3总传动误差直方图

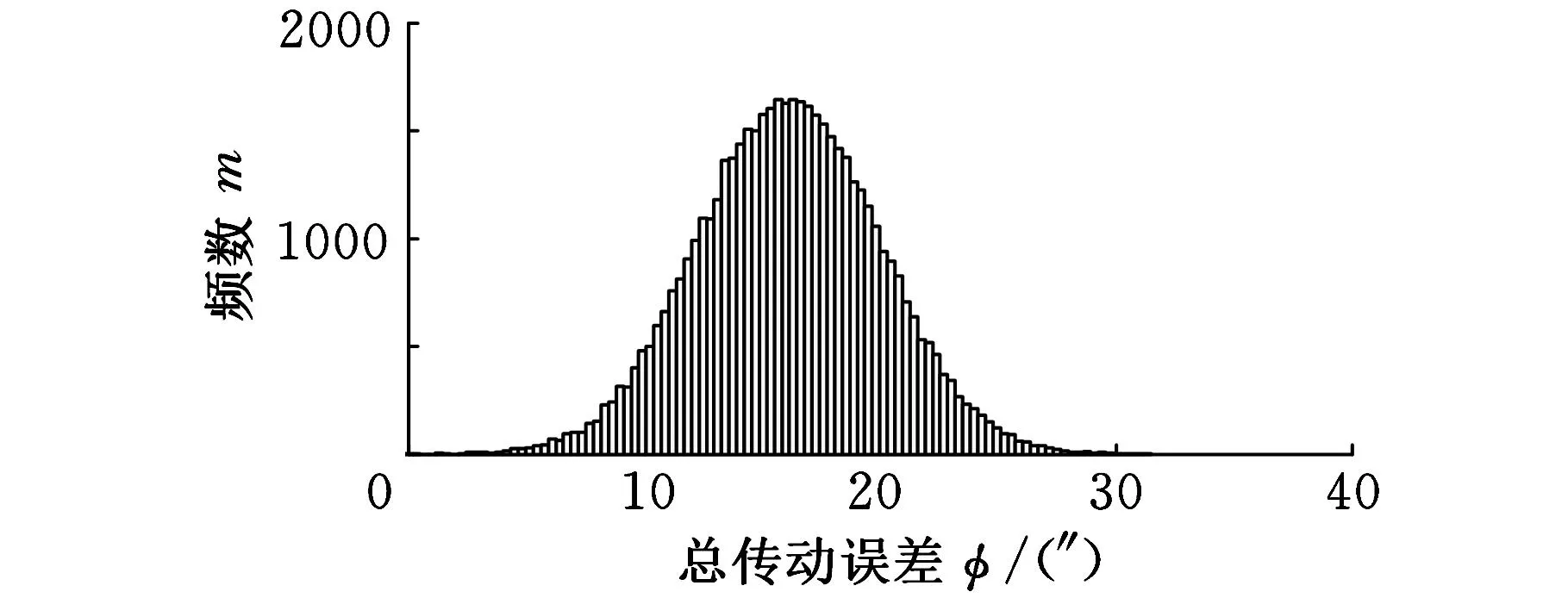
(c)HM4总传动误差直方图

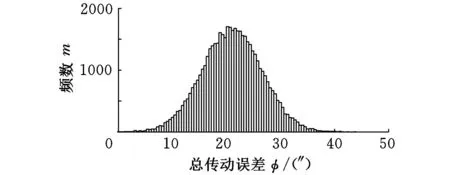
(d)HM5总传动误差直方图图3　各挡位总传动误差直方图

比较图3a和图2，蒙特卡罗法得到的HM2挡总传动误差最小值为0″，最大值为30.51″，期望为15.8″，标准差为15.22″，取置信系数为0.9973，可得置信区间为[0″,16.00″]。图2中，总传动误差最小值为0″，与蒙特卡罗法得到的最小值相同，最大值为31.83″，比蒙特卡罗法得到的最大值略大1.32″，由于蒙特卡罗法得到的总传动误差直方图近似符合正态分布，可得HM2挡总传动误差的值在16.00″内的概率为99.73%。

比较图3b和图2，蒙特卡罗法得到的HM3挡总传动误差最小值为0″，最大值为55.71″，期望为25.96″，标准差为50.21″，取置信系数为0.9973，可得置信区间为[0″,26.58″]，图2中，总传动误差最小值为0″，与蒙特卡罗法得到的最小值相同，最大值为57.92″，比蒙特卡罗法得到的最大值略大2.21″，由于蒙特卡罗法得到的总传动误差直方图近似符合正态分布，可得HM3挡总传动误差的值在26.58″内的概率为99.73%。

比较图3c和图2可得，蒙特卡罗法得到的HM4挡总传动误差最小值为0″，最大值为30.49″，期望为16.1″，标准差为14.95″，取置信系数为0.9973，可得置信区间为[0″,16.29″]，图2中，总传动误差最小值为0″，与蒙特卡罗法得到的最小值相同，最大值为30.89″，比蒙特卡罗法得到的最大值略大0.40″，由于蒙特卡罗法得到的总传动误差直方图近似符合正态分布，可得HM4挡总传动误差的值在16.29″内的概率为99.73%。

比较图3d和图2可得，蒙特卡罗法得到的HM5挡总传动误差最小值为0″，最大值为44.03″，期望为20.96″，标准差为30.21″，取置信系数为0.9973，可得置信区间为[0″,21.34″]，图2中，总传动误差最小值为0″，与蒙特卡罗法得到的最小值相同，最大值为44.49″，比蒙特卡罗法得到的最大值略大0.46″，由于蒙特卡罗法得到的总传动误差直方图近似符合正态分布，可得HM4挡总传动误差的值在21.34″内的概率为99.73%。

通过比较可知，各挡位的总传动误差与蒙特卡罗抽样得到的总传动误差相比，最小值相同，最大值略大，误差值基本满足正态分布规律，各挡位的总传动误差值99.73%落在置信区间内。可得此变速器总传动误差的分布规律基本符合蒙特卡罗法得到的误差分布规律。

5传动误差对功率的影响

对齿轮所转的圈数与时间的函数求导，可得齿轮的转速与时间的函数，依照转速与功率的关系可得瞬时功率损耗与时间的函数关系式：

(25)

式中，T0为扭矩；P为瞬时功率损耗；( )′表示求导。

从式(25)中可得瞬时功率损耗与总传动误差存在正比关系。以前进挡HM3为研究对象，可得其功率损耗随时间的变化规律，如图4所示。从图4中可看出HM3挡在1.25 s时瞬时功率损耗最大，约为0.78 W。

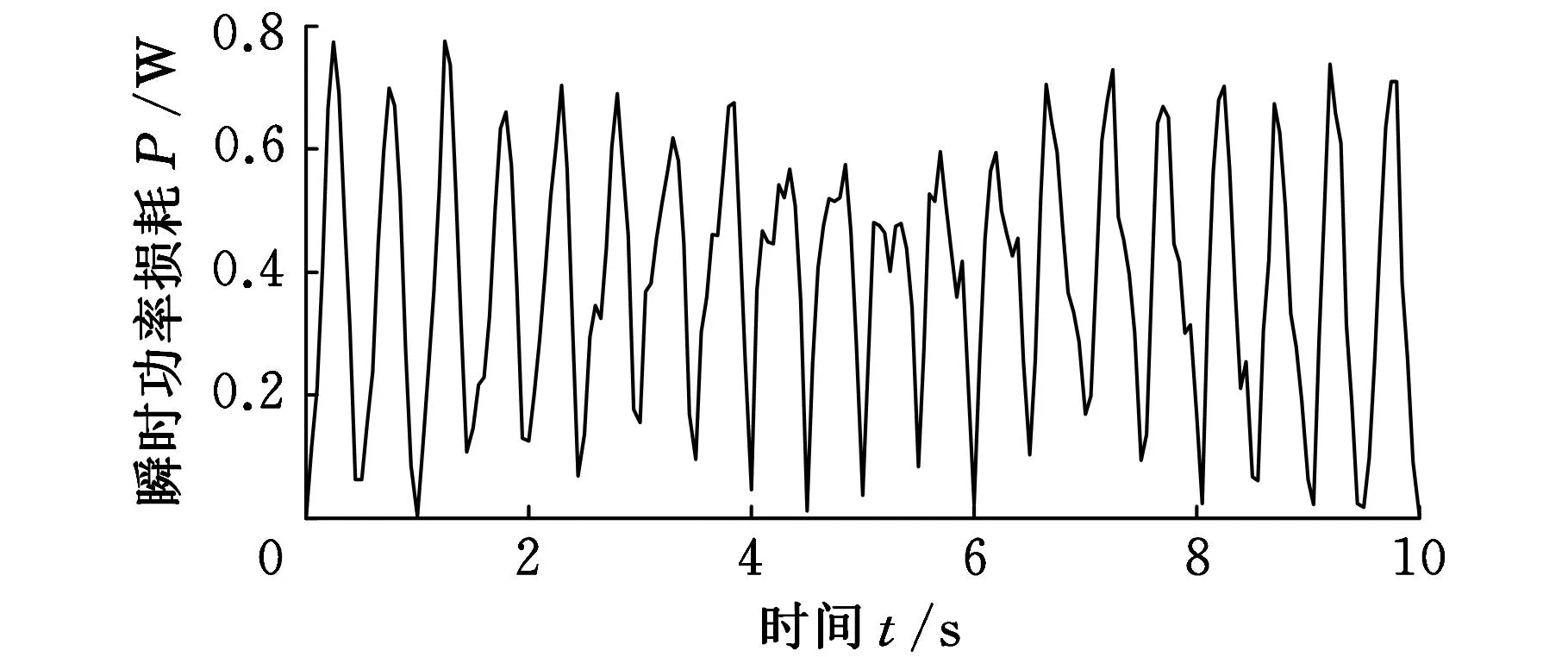
图4　HM3挡瞬时功率损耗变化规律

以此挡位为研究对象，在安装定轴齿轮z3时，使其安装误差的初相与K2的内齿圈制造误差的初相所成角度从0°到360°变化，可得在1.25 s时刻，HM3挡的瞬时功率损耗的变化规律，如图5所示。

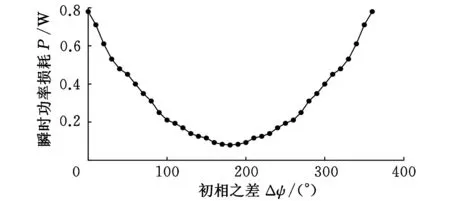
图5　耦合后HM3挡瞬时功率损耗的变化规律

由图5可知，耦合前HM3挡瞬时功率损耗在1.25 s时为0.78 W，耦合后HM3挡瞬时功率损耗随着z3安装误差的初相与K2的内齿圈制造误差的初相所成角度的变化而变化，在[0°,180°]之间，瞬时功率损耗逐渐减小，在[180°,360°]之间，瞬时功率损耗逐渐增大，在初相之差为180°时，瞬时功率损耗最小为0.079 W，约为耦合前瞬时功率损耗的10.13%，大大减小了瞬时功率损耗。

6结论

(1)选取东方红某型号拖拉机的液压机械无级变速器为对象，研究了其机械变速机构的行星齿轮组、定轴齿轮副和两者共同作用时的传动误差，得到传动误差随时间的变化规律。

(2)行星齿轮传动误差和定轴齿轮副传动误差会出现角频率相同的情况，此时两者存在耦合关系。耦合误差的大小由各误差分量的误差值决定。各误差分量的初始相位之差决定了误差分量之间的抵消程度。

(3)该变速器瞬时总传动误差最大、最小的挡位是HM3、HM4，两者相差明显。在对输出速度要求不高的情况下，应尽量使拖拉机在HM4下作业，避免在HM3下作业。

(4)总传动误差的主导因素是行星齿轮组传动误差。在时间相同时，后退挡的传动误差与相应前进挡的传动误差大小相等方向相反，满足前进挡的一切规律性。

(5)变速器总传动误差的分布规律基本符合蒙特卡罗法得到的误差分布规律。研究所得规律可用于分析类似的齿轮传动机构的传动误差。

(6)由于总传动误差的主导因素是行星齿轮组传动误差，HM3挡的总传动误差是所有挡位中最大的，在HM3挡中，参加工作的行星齿轮组是K2，可知K2是影响总传动误差最为严重的齿轮。

(7)传动误差与瞬时功率损耗存在正比关系。在装配时，使角频率相同的各传动件误差初相所成角度在90°~180°间,能减小瞬时功率损耗，所成角度为180°时，瞬时功率损耗最小。

参考文献：

[1]徐立友, 周志立, 彭巧励, 等. 多段式液压机械无级变速器方案设计与特性分析[J]. 中国机械工程, 2012,23(21): 2641-2645.

Xu Liyou, Zhou Zhili, Peng Qiaoli, et al. Drive Scheme Design and Characteristic Analysis of Multi-range Hydro-mechanical CVT[J]. China Mechanical Engineering, 2012, 23(21): 2641-2645.

[2]日高照晃, 王宏猷, 石田武. ほか.サイクロイド齒車を用ぃたK-H-V形遊星齒車装置の回转传达误差に开する研究(第1报,解析方法)[C]//日本耭械学会论文集(C编).东京, 1994: 645-653.

[3]Blanche J G, Yang D C. Cycloid Drives with Machining Tolerances[J]. AEME Journal of Mechanisma, Transmissions, and Automation in Design, 1989,111(9):337-344.

[4]Litvin F L, Gonzalezpere I, Fuentes A, et al. Topology of Modified Surfaces of Involute Helical Geras with Line Contact Developsd for Improvement of Bearing Contact,Reduction of Transmission Errors, and Stress Analysis[J]. Mathematical and Computer Modelling, 2005, 42(5): 1063-1078.

[5]Nagahata D, Hendricx W, Anthonis J, et al. Reducing Gear Whine of a Valtra Continuous Variable Transmission[C]//VDI-MEG.Hanover, 2009: 113-122.

[6]Pears J, Smith A, Curtis S. A Software Tool for the Prediction of Planetary Gear Transmission Error[C]//VDI Beriche.Hanover, 2005: 357-372.

[7]Kahramn A. Load Sharing Characteristics of Planetary Transmission[J]. Mech. Mach. Theory, 1994, 29(8): 1151-1161.

[8]Kahramn A. Static Load Sharing Characteristics of Transmission Plametary Gear Sets, Model and Experiment, Society of Automotive Engineers[J].SAE Paper,1999-01-1050.

[9]邵晓荣. 齿轮制造及安装误差对行星齿轮传动的影响[J]. 东北重型机械学院学报, 1994, 18(4): 306-309.

Shao Xiaorong. Influence of Load Sharing Coefficient on the Manufacture and Assemble Error of the Planetry Gear NGW[J]. Journal of Northeast Heavy Machinery Institute, 1994, 18(4): 306-309.

[10]Parker R G, Lin Jian. Modeling, Modal Properties, and Mesh Stiffness Variation Instabilities of Planetary Gears[J].Journal of Tribology, 2001:NASA/CR-2001-210939.

[11]王朝兵, 陈小安, 李云松, 等.行星齿轮传动误差的耦合补偿研究[J]. 农业机械学报, 2013, 44(8): 287-292.

Wang Chaobing, Chen Xiaoan, Li Yunsong, et al. Coupling Compensation of Transmission Error for Planetary Gear[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(8): 287-292.

[12]林长洪, 朱家诚. 齿轮传递误差计算的分析[J]. 设计与研究, 2011, 8(38): 10-13.

Lin Changhong, Zhu Jiacheng. The Calculation of Transmission Error of Gear[J]. Design and Research, 2011, 8(38): 10-13.

[13]阮登芳, 李强军, 张绪勇, 等. 重型汽车变速器后置副变速器换挡同步时间分析[J]. 中国机械工程, 2013, 24(22): 3105-3109.

Ruan Dengfang, Li Qiangjun. Zhang Xuyong, et al. Analysis on Shifting Synchronous Time of Rear Auxiliary Transmission for a Heavy-duty Truck Transmission[J]. China Mechanical Engineering, 2013, 24(22): 3105-3109.

[14]中国一拖集团. 液压机械无级变速器技术报告[R]. 洛阳: 中国一拖集团技术中心, 2011.

[15]刘志忠, 柳洪义, 罗忠, 等.机器人工作空间求解的蒙特卡洛法改进[J]. 农业机械学报，2013，44(1):230-235.

Liu Zhizhong, Liu Hongyi, Luo Zhong, et al. Improvement on Monte-Carlo Method for Robot Workspace Determination[J].Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(1):230-235.

(编辑袁兴玲)

Analyses of Transmission Error of Mechanical Shift Gear in HMCVT

Lei XianqingCai ZhenhuaZhang MingzhuMa Wensuo

Henan University of Science & Technology,Luoyang,Henan,471003

Abstract:Based on the mechanical shift gear in HMCVT of Dongfanghong,the rules of the transmission error changing with time were researched to reduce the power loss of the transmission. The formula among transmission errors of planetary gear set, fixed-axle gear pair,the two factor function simultaneously and time were established by using the theory of equivalent mesh error. The gear which had the transient maximum and the minimum transmission errors and the dominant factor of transmission errors were found by comparing the whole transmission error and the transmission errors of planetary gear set. There existed coupling relationship among the transmission errors of planetary gear set and fixed-axle gear pair when the angular frequency was the same. The correctness of the rules was verified by using the Monte-Carlo method. The formula among transmission errors and power loss was established. It turns out that there is positive relationship among them. The measures which reduce the power loss of transmission were put forward by using the method which was used to reduce the transmission errors.

Key words:tractor; hydro-mechanical continuous variable transmission (HMCVT); transmission error; Monte-Carlo method; power loss

基金项目：国家自然科学基金资助项目(51375145)

收稿日期：2015-03-02

中图分类号：S219.032.1DOI：10.3969/j.issn.1004-132X.2015.23.022

作者简介：雷贤卿，男，1963年生。河南科技大学机电工程学院教授、博士研究生导师。蔡振华，男，1989年生。河南科技大学机电工程学院硕士研究生。张明柱，男，1964年生。河南科技大学机电工程学院教授、博士研究生导师。马文锁，男，1969年生。河南科技大学机电工程学院教授、博士研究生导师。