冗余驱动支链对3RPS并联机构刚度的改善

崔学良　陈五一　韩先国　祝锡晶　王建青　成　全

1.中北大学，太原，030051　　2.北京航空航天大学，北京，100191



冗余驱动支链对3RPS并联机构刚度的改善

崔学良1陈五一2韩先国2祝锡晶1王建青1成全1

1.中北大学，太原，0300512.北京航空航天大学，北京，100191

摘要：在考虑雅可比矩阵变化与动平台姿态偏移之间映射关系的基础上，基于螺旋理论和矢量微分法建立了3RPS并联机构末端位姿偏移与支链构件变形之间的映射模型。首先采用螺旋理论和矢量微分法分析了支链各构件刚度与整个支链刚度之间的关系，然后建立了3RPS并联机构的瞬时刚度模型，并分析了雅可比矩阵的变化对机构刚度的影响。对冗余驱动支链改善并联机构刚度的原理进行了分析，建立了冗余驱动并联机构的整机刚度模型。仿真分析和实验验证，冗余驱动支链确实能够改善并联机构的刚度。

关键词：冗余驱动；瞬时刚度模型；矢量微分法；并联运动机构；位姿偏移

0引言

少自由度并联机构结构简单，控制方便，具有广阔的工程应用前景。但由于各支链同时受拉和受弯，因此更易产生变形，这导致并联机构整体刚度变弱，末端精度变差。同时，由于并联机构耦合严重，故难以设计全闭环控制系统以对其位姿偏差进行有效补偿。鉴于此，人们提出增加冗余驱动支链来提高并联机构刚度的方法。文献[1-2]对平面并联机构进行了刚度分析、参数优化和动力学等方面研究，并采用有限元方法进行了相关分析验证。文献[3-4]中，研究者针对不同的空间并联机构，提出了增加冗余驱动支链以改善并联机构刚度的策略，并进行了相应的分析和验证。文献[5-6]分别基于虚功原理和能量守恒定理研究了冗余驱动并联机构的完整刚度模型和所有支链的弹性变形协调方程。文献[7]通过对含驱动和被动冗余支链的三自由度并联机构进行对比分析，得出了冗余驱动支链能够提高并联机构刚度的结论。文献[8-9]对冗余驱动并联机构进行了驱动支链和整机刚度分析，并对冗余驱动支链的协调驱动力进行了优化设计。

3RPS并联机床作为一种实用化程度较高的并联机构，已应用于航空、汽车等制造装配领域，但其刚度、精度等指标并不比传统机床高。本课题组研制了3RPS+UPS冗余驱动并联机床，通过合理布置冗余驱动支链可在消除部分奇异、增大姿态能力的同时改善整机的刚度。本文分析研究冗余驱动支链对并联机构刚度改善作用的机理。通过与非冗余驱动并联机构刚度模型比较分析可知，增加冗余驱动支链确实可提高并联机构的刚度。

13RPS+UPS冗余驱动并联机构结构简介

3RPS+UPS并联机构结构及坐标系如图1所示。其中，oxyz为参考坐标系，puvw为随动坐标系。UPS支链为冗余驱动支链，其中的胡克铰U连接支链与静平台，U副中点B4位于静平台几何中心；移动副P为冗余支链l4的驱动副，球铰S连接冗余支链与动平台，球心b4位于动平台中心p。

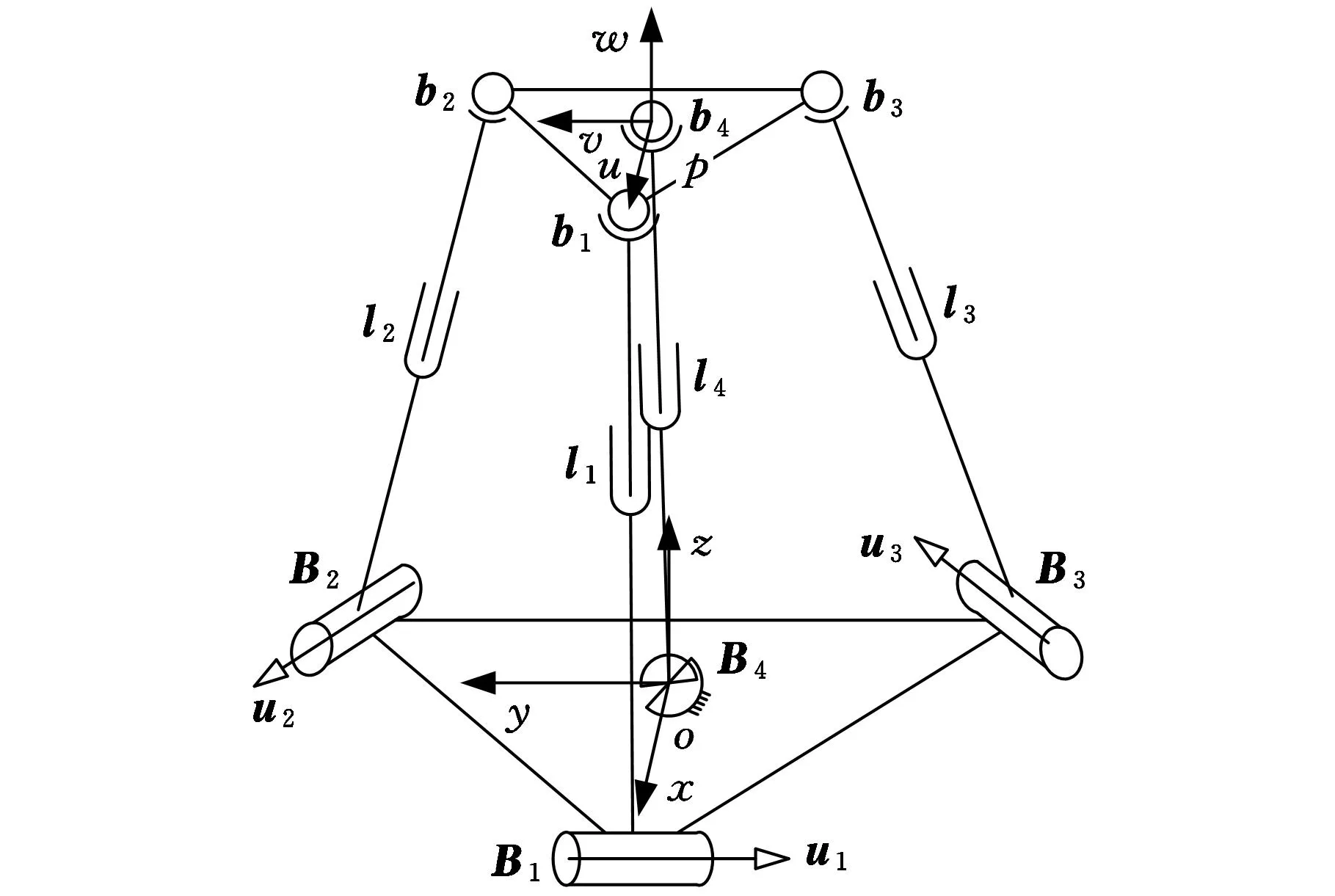
图1　3RPS+UPS冗余驱动并联机构

23RPS并联机构刚度模型

2.13RPS并联机构力平衡分析

力平衡分析是并联机构刚度模型建立的基础。3RPS并联机构的受力平衡方程为

F+Jflfl=0

(1)

式中，F为动平台所受外载荷；Jfl为3-RPS并联机构的力雅可比矩阵，由各支链的轴向和切向作用力单位线矢组成；fl为各支链对动平台作用力大小所构成的矢量。

2.2支链刚度分析

支链采用伺服电机加滚珠丝杠螺母副作为驱动机构；为提高支链运动的直线度，采用直线导轨作为移动导向机构。滚珠丝杠螺母系统包括丝杠、螺母、滑块、直线导轨和轴承，丝杠与直线导轨固接在同一基座上，丝杠两端由轴承分别与基座连接，支链结构如图2所示。丝杠、直线导轨和基座的轴向和侧向刚度是影响支链刚度的主要因素。

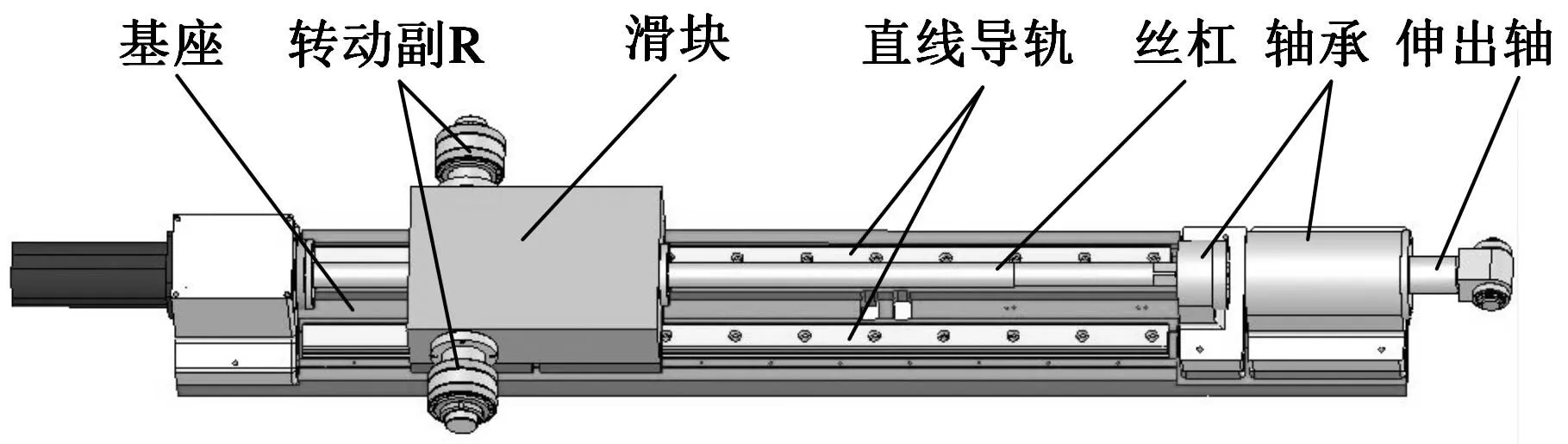
图2　RPS支链结构图

由图2可见，支链中的丝杠和轴承组成一个串联系统，分别记其轴向和侧向刚度为kda和kdt，则有

(2)

式中，ksa、kst分别为该串联系统中丝杠的轴向和侧向刚度；kca、kct分别为轴承的轴向和径向刚度。

丝杠和直线导轨组成一个并联系统，分别记其轴向和侧向刚度为kpa和kpt。图2中，直线导轨固接在基座上，记导轨与基座结合体的轴向和侧向刚度分别为kga和kgt，则有

(3)

支链末端由一个伸出轴与球铰相连，该伸出轴由轴承和丝杠导轨系统连接，从而组成整个支链。记支链总的轴向和侧向刚度分别为kla和klt，则有

(4)

式中，kza、kzt分别为支链前端伸出轴的轴向和侧向刚度。

2.3支链弹性变形与动平台位姿关系

设3RPS并联机构变形前动平台中心在参考坐标系中为p，铰链球心在动平台随动坐标系中的位置为pbi。则由位置反解模型可知，3RPS并联机构在变形前满足几何约束方程:

Bi+li=p+Rpbii=1, 2, 3

(5)

式中，Bi为并联机构参考坐标系原点到支链转动副R转轴中点的矢径；li为当前位姿时支链矢径；R为动平台的姿态矩阵。

当外载荷发生变化时，设动平台中心位置由p变为p′(p′=p+δp)；其姿态矩阵由R变为R′(R′=R+δR)，则有

Bi+li+δli=p+δp+(R+δR)pbi

(6)

其中，δli为支链li在外作用力下的弹性变形量，包括轴向和侧向变形量；δp为机构变形后动平台随动坐标系原点位置的偏移微量；δR为机构变形后动坐标系姿态的偏移微量。由机器人机构学可知，动平台姿态的偏移量δR可等效为随动坐标系绕过其原点的某一转轴转过一个微小角度δθ，其等效微分旋转变换矩阵满足关系式δRpbi=δθ×Rpbi。

由式(5)和式(6)可得

δli=δp+δθ×Rpbi

(7)

式(7)两端分别点乘lai和lti(i=1, 2, 3)并整理，可得并联机构动平台位姿偏移与支链li弹性变形之间的几何约束方程:

δl=JvlδD

(8)

Jvl=

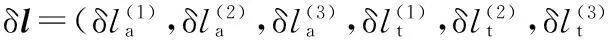
2.43RPS并联机构瞬时刚度模型

对式(1)进行全微分，并考虑到支链li(i=1, 2, 3)在外载荷下的弹性变形关系式δfl=-klδl，当δJfl≠0时，可得

(9)

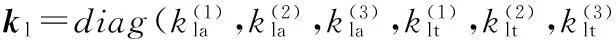
由机构学可知

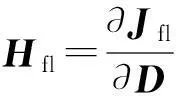
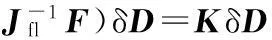
(10)

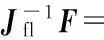
其中，符号“⊗”表示矩阵的张量积；K为并联机构的整体刚度矩阵。当矩阵Jfl非奇异时，由式(10)可得支链li弹性变形与动平台位姿偏移量之间的关系式：

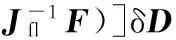
(11)

由式(8)，并结合式(11)，可得机构整机刚度矩阵：

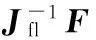
(12)

忽略雅可比矩阵变化量对机构整体连续刚度的影响，即令δJfl=0，且将此时机构整机刚度记为Kl，则式(12)可进一步简化为

Kl=JflklJvl

(13)

式(13)即为典型的并联机构简化刚度模型。

3冗余驱动支链对并联机构刚度的改善

由上面分析可知，少自由度并联机构支链需同时对动平台提供约束力和驱动力，已不再是单纯的二力杆，在载荷作用下容易产生变形，从而影响机构的整体刚度。为此，人们提出增加冗余驱动支链的方法来改善并联机构的整机刚度。本节以3RPS+UPS冗余驱动并联机构为例，对冗余驱动支链能提高并联机构刚度的原理进行分析和研究。

3.1冗余驱动并联机构各支链运动协调关系

3RPS+UPS并联机构结构如图1所示。取动平台为研究对象，其作用力平衡关系如图3所示。

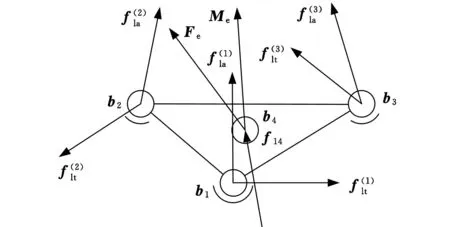
图3　冗余驱动并联机构动平台受力图

由矢量投影法，建立3RPS+UPS冗余驱动并联机构动平台上的力平衡方程如下：

(14)

将式(14)写成矩阵形式，有

Gff=F

(15)

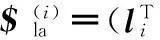
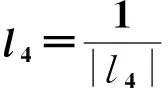
δl4=l4·δD

(16)

由式(8)和式(16)，可得冗余驱动支链与非冗余驱动支链之间的变形协调关系为

(17)

3.2冗余驱动并联机构整机刚度模型

由虚功原理可得

(18)

(19)

冗余驱动UPS支链的驱动系统包括丝杠、螺母和轴承，令支链中丝杠、螺母和轴承的轴向刚度分别为ks、kn和kb，且记其轴向刚度为kl4，则有

(20)

从而可得

fl4=kl4δl4

(21)

由式(18)~式(21)，并结合式(15)~式(17)可得

(22)

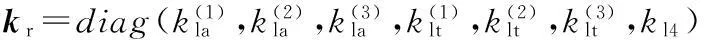
由此可得冗余驱动并联机构的外载荷与其动平台位姿偏移量的映射关系为

(23)

3.3冗余驱动支链对并联机构刚度的改善

为评价冗余驱动对并联机构刚度指标的影响，分别计算冗余驱动并联机构和非冗余驱动并联机构刚度模型在相同外载荷下末端位姿偏移量的大小。支链的刚度与其长度有关，设冗余驱动并联机构的冗余驱动支链l4的轴线刚度为4.824×109/|l4|N/mm，其余参数同非冗余驱动并联机构(表1)。结果如图4所示。

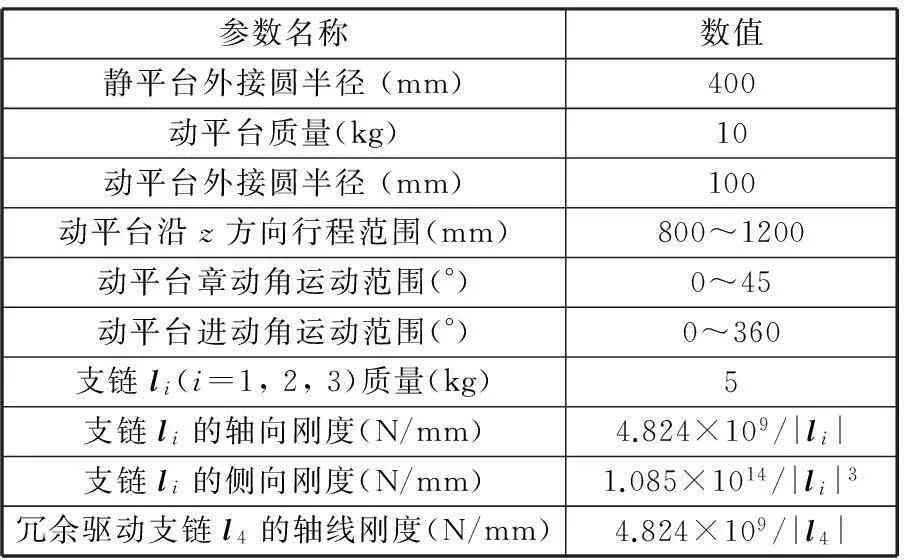
表1　3RPS+UPS冗余驱动并联机构的参数

注：表中|li|为由并联机构当前位姿决定的支链瞬时长度。

由图4可看出，在相同外载荷作用下，冗余驱动并联机构末端位姿偏移量小于非冗余驱动并联机构的位姿偏移量，表明采用冗余驱动的确能够提高并联机构的刚度。

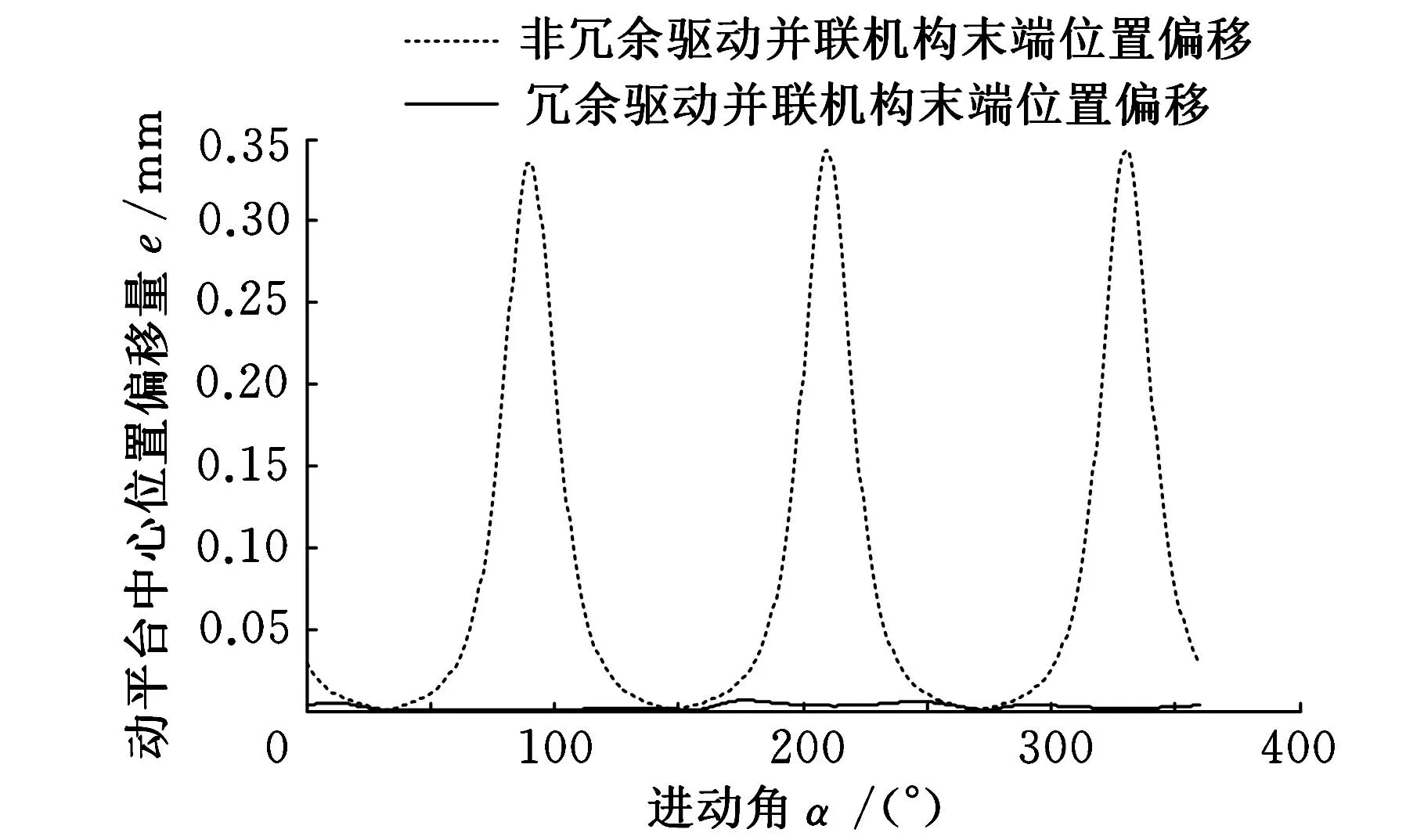
(a)章动角为45°，z向距离为0.8 m

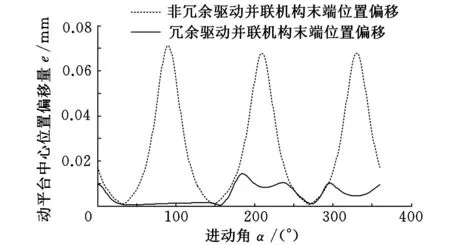
(b)章动角为45°，z向距离为1.2 m

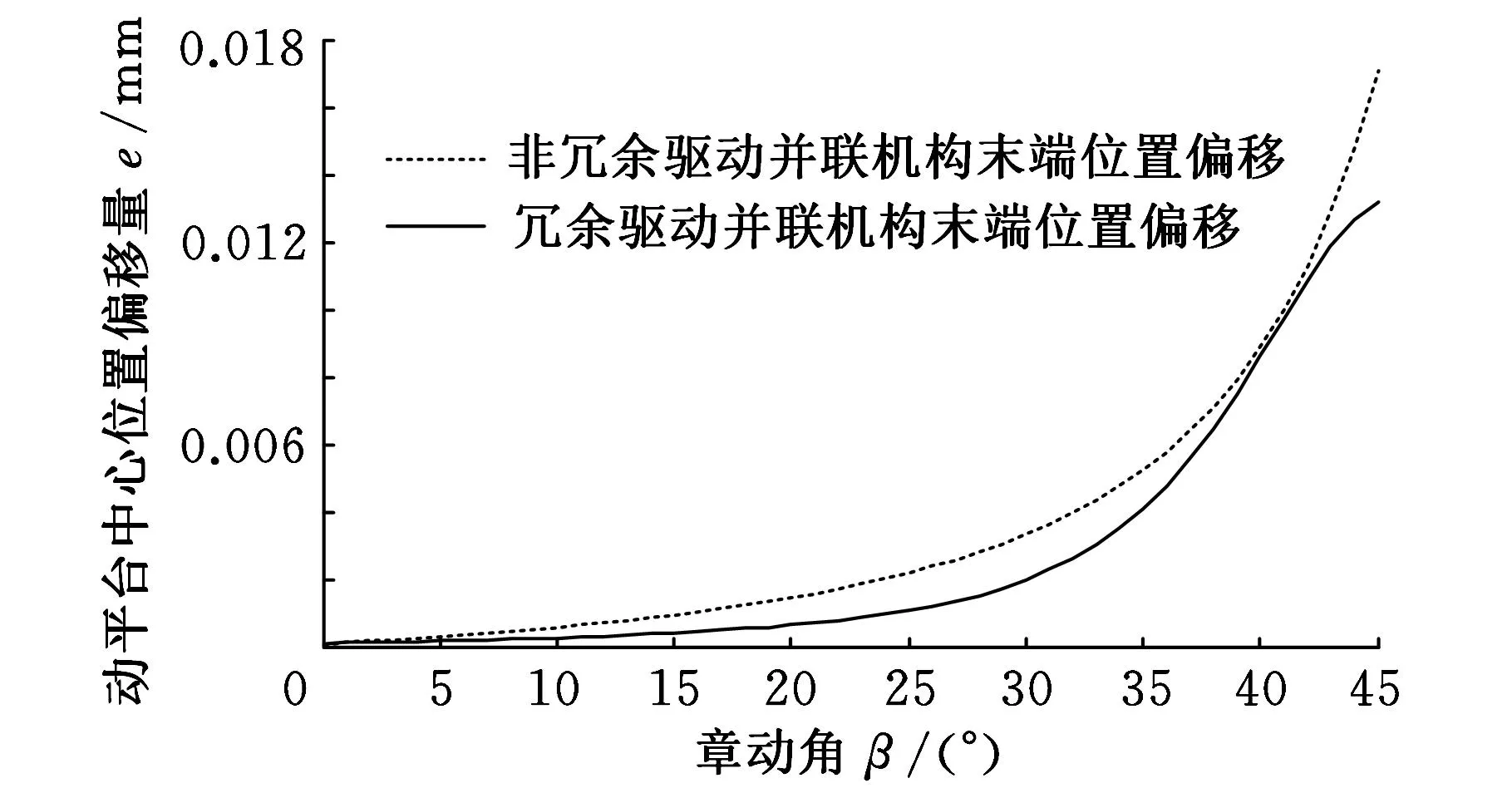
(c)进动角为180°，z向距离为0.8 m

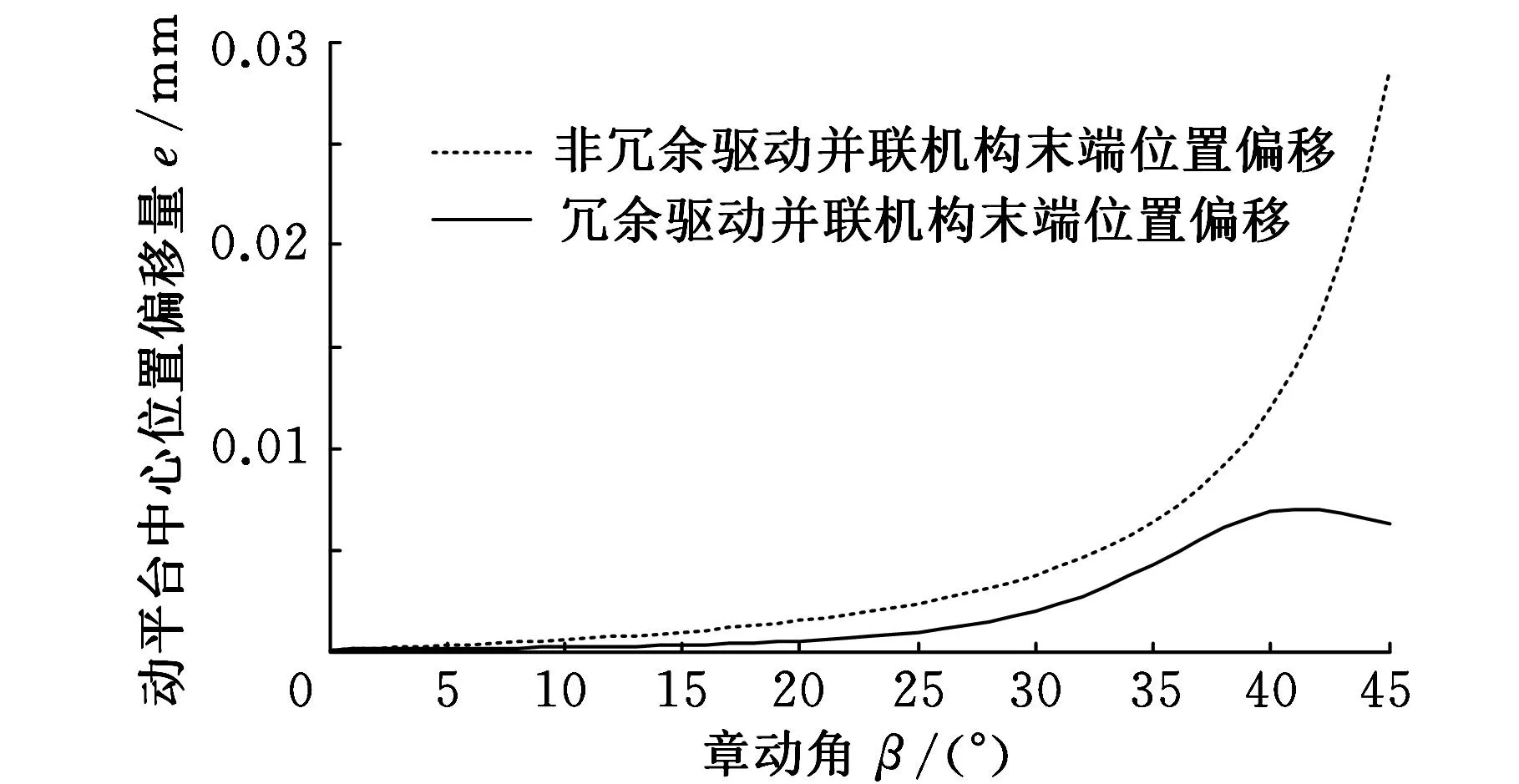
(d)进动角为180°，z向距离为1.2 m图4　不同位姿处冗余驱动与非冗余驱动并联机构刚度的比较

4实验验证

以本课题组研制的3PRS+UPS冗余驱动并联机构为例，分别测量不加冗余驱动支链和增加冗余驱动支链时机构的末端刚度。通过比较二者的差别，考察冗余驱动支链对并联机构刚度的影响。实验采用砝码+千分表的方案，图5和图6是测量水平和垂直刚度的实验照片。其中，刚度测量中的外力是用外挂砝码实现的，通过专用夹具将外力作用在动平台中心；动平台上粘结了一个圆球，以便在不同姿态时，用千分表都能测量到动平台沿水平或垂直方向的位移。测量结果如表2、表3所示。

图5　不含冗余支链时　图6　含冗余支链时　　　机构刚度测量　　 机构刚度测量

5结论

(1) 采用螺旋理论和矢量微分法分析了3RPS并联机构支链及复合铰链在外载荷及自重力作用下的弹性变形，建立了机构末端位姿偏移与支链构件变形的映射关系。

(2) 考虑支链弹性变形影响，建立了并联机构瞬时刚度模型。分析了雅可比矩阵的变化对机构的刚度影响，当动平台处于其姿态空间边界处时，其影响尤为明显。

(3) 对冗余驱动支链改善并联机构刚度的原理进行了分析，建立了冗余驱动并联机构各支链的运动协调关系，仿真计算和实验证明了冗余驱动支链能够提高并联机构的整机刚度。

表2　机构水平刚度测试

表3　机构垂直刚度测试

参考文献：

[1]WuJun,WangJinsong,WangLiping.DynamicsandControlofaPlanar3-DOFParallelManipulatorwithActuationRedundancy[J].MechanismandMachineTheory, 2009, 44: 835-849.

[2]WangSongtao,ChengGang,PangYusong,etal.IntegratedStiffnessAnalysisofRedundantParallelManipulatorBasedonFiniteElementMethod[J].JournalofInformation&ComputationalScience, 2015, 12(1): 351-365.

[3]白志富，陈五一. 球铰刚度计算模型及靠冗余支链实现并联机床刚度的改善[J]. 机械工程学报, 2006, 42(10): 142-145.

BaiZhifu,ChenWuyi.StiffnessComputationModelofSphericalJointsandPKM’sStiffnessImprovementbyRedundantLeg[J].ChineseJournalofMechanicalEngineering, 2006, 42(10): 142-145.

[4]宋轶民，翟学东，孙涛,等. 一种三自由度冗余驱动并联模块的刚度分析[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(1): 25-32.

SongYimin,ZhaiXuedong,SunTao,etal.StiffnessAnalysisofa3-DOFRedundantlyActuatedParallelModule[J].JournalofTianjinUniversity(ScienceandTechnology), 2015, 48(1): 25-32.

[5]周鑫，许允斗，姚建涛,等. 5-UPS/PRPU冗余驱动并联机床完整刚度模型及其刚度特性[J]. 光学精密工程，2015，23(4):1070-1080.

ZhouXin,XuYundou,YaoJiantao,etal.CompleteStiffnessModelandStiffnessPerformanceof5-UPS/PRPURedundantlyActuatedParallelMachineTool[J].OpticsandPrecisionEngineering, 2015，23(4):1070-1080.

[6]XuYundou,YaoJiantao,ZhaoYongsheng.InverseDynamicsandInternalForcesoftheRedundantlyActuatedParallelManipulators[J].MechanismandMachineTheory, 2012, 51: 172-184.

[8]JinSangrok,KimJongwon,SeoTaeWon.OptimizationofaRedundantlyActuated5RSymmetricalParallelMechanismBasedonStructuralStiffness[J].Robotica, 2015, 7: 1-11.

[9]窦玉超，姚建涛， 高思慧,等. 冗余驱动并联机器人动力学建模与驱动力协调分配[J]. 农业机械学报,2014， 45(1)：293-299.

DouYuchao,YaoJiantao,GaoSihui,etal.DynaimicModelingandDrivingForceCoordinateDistributionoftheParallelRobotwithRedundantActuation[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2014，45(1)：293-299.

(编辑袁兴玲)

Stiffness Improvement of 3RPS PKM by Redundant Actuating Leg

Cui Xueliang1Chen Wuyi2Han Xianguo2Zhu Xijing1Wang Jianqing1Cheng Quan2

1.North University of China，Taiyuan,030051

2. Beihang University,Beijing,100191

Abstract:Considering the relationship between the changes of the Jacobian matrix and the orientation deviation of the moving platform, the mapping model between the 3RPS PKM end-effector offset and the deformation of the branches was established by using the vector differential method, based on the screw theory. The functional expression of the rigidity of the chain and its components was derived, and then the instant stiffness model of the 3RPS PKM was built up. The influences of the changes of the Jacobian matrix on the stiffness of the PKM were analyzed. The theories that the redundant actuating leg could increase the stiffness of the PKM were discussed, and were also verified by the simulation and the tests.

Key words:redundant actuation; instant stiffness model; vector differential method; parallel kinematic machanism(PKM);position and orientation offset

收稿日期：2015-07-30

中图分类号：TH112DOI：10.3969/j.issn.1004-132X.2015.23.008

作者简介：崔学良，男，1971年生。中北大学机械与工程学院讲师。研究方向为精密与特种加工技术。发表论文4篇。陈五一，男，1951年生。北京航空航天大学机械工程及自动化学院教授。韩先国，男，1970年生。北京航空航天大学机械工程及自动化学院副教授。祝锡晶，男，1969年生。中北大学机械与工程学院教授。王建青，女，1973年生。中北大学机械与工程学院副教授。成全，男，1969年生。中北大学机械与工程学院讲师。