自适应特征尺度分解方法及其应用
2016-01-28吴占涛程军圣
吴占涛 程军圣 杨 宇
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
自适应特征尺度分解方法及其应用
吴占涛程军圣杨宇
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
摘要:针对局部特征尺度分解(LCD)存在的模态混叠问题和其在均值曲线定义方面存在的不足,在对LCD方法研究的基础上,充分借鉴经验模态分解(EMD)和LCD等此类基于筛分的信号分解方法的思路,定义了一种新的瞬时频率具有物理意义的单分量信号——内禀致密尺度分量(ICC),并提出了一种新的自适应信号分解方法——自适应特征尺度分解(ACD)方法。同时,给出了ICC分量评价准则,通过对ACD每阶筛分中由不同均值曲线和致密系数取值得到的一组不同的分解分量进行对比,选取最优分量作为该阶筛分的ICC分量,从而保障最终分解效果优于LCD方法分解效果。对仿真信号的分析结果证实了ACD方法的分解效果优于EMD、LCD、总体平均经验模态分解(EEMD)和自主致密局部特征尺度分解(ACLCD)方法的分解效果;对实验数据的分析结果验证了ACD的有效性,从而为旋转机械故障诊断提供了一种新的方法。
关键词:自适应特征尺度分解;局部特征尺度分解;经验模态分解;内禀致密尺度分量;故障诊断
0引言
机械设备发生故障时会产生大量的非平稳信号,对此类信号的分析一直是相关学者关注的热点。近年来,小波分析(wavelet analysis,WA)、经验模态分解(empirical mode decomposition,EMD)方法和局部均值分解(local mean decomposition,LMD)方法等时频分析方法由于适合处理复杂的振动信号,均已被应用于机械故障诊断领域,并取得了许多有益的研究成果[1-3],但这些方法都具有一定的局限性。局部特征尺度分解(local characteristic-scale decomposition,LCD)方法是最近提出的一种自适应时频分析方法[4]。该方法在定义瞬时频率具有物理意义的单分量信号——内禀尺度分量(intrinsic scale component,ISC)基础上,通过提取数据本身的特征尺度参数,可自适应地将复杂信号分解为若干个ISC分量之和。相对于EMD和LMD方法,LCD方法在分解速度、抑制端点效应和模态混叠等方面具有一定的优势,已在信号分析和机械故障诊断等领域得到了有效的应用[5-6]。但尽管如此,由于LCD方法理论基础尚不完善,实际应用中也存在同一尺度或频率的信号被分解到多个不同的ISC分量当中,或一个ISC分量中出现了尺度或频率差异较大的信号的模态混叠现象[7];同时,LCD均值曲线的插值点是由连接两相邻同类极值点的连线计算产生的,虽然相对于EMD方法减小了迭代计算量、提高了分解精度,但由于均值曲线插值点的属性主要由相邻两同类极值点的属性决定,不能很好地体现数据的整体变化趋势,从而可能引起分解精度降低,因此有待进一步改进。
LCD分解发生模态混叠的主要原因是原始信号的极值尺度差异较大,且幅值不同。为抑制LCD方法的模态混叠,笔者曾提出了自主致密局部特征尺度分解(autonomous compact local characteristic-scale decomposition,ACLCD)方法[8]。ACLCD方法采用新增伪极值点实现对原始信号的信号尺度均匀化,提高分解精度,有效抑制模态混叠产生。然而,ACLCD方法采用的仍是LCD方法的均值曲线,因而也存在LCD方法中由均值曲线定义的不足导致的固有缺陷。由上述分析可知,ACLCD方法的分解结果并非最优,且可能引起新的分解误差。EMD和LCD等这类基于筛分的信号分解方法有着共同的分解思路,即在定义瞬时频率具有物理意义的单分量信号的基础上,定义一种基于均值曲线的筛分过程,通过筛分过程不断地从原始信号中分离出相对高频的分量。这类基于筛分的信号分解方法核心问题是如何定义合理的均值曲线,均值曲线定义的优劣直接决定了方法的有效性和精确性[9]。
本文在对LCD方法研究的基础上,充分借鉴ACLCD方法的优势与EMD和LCD等这类基于筛分的信号分析方法的思路,采用典型的数值计算方法定义了5种不同的均值曲线,并采用与ACLCD方法相同的思路新增伪极值点以均匀化信号尺度,定义了一种新的瞬时频率具有物理意义的单分量信号——内禀致密尺度分量(intrinsic compact-scale component,ICC)。基于此,提出了一种新的自适应信号分解方法——自适应特征尺度分解(adaptive characteristic-scale decomposition,ACD)方法。同时,给出了ICC分量评价准则,通过对ACD每阶筛分中由不同均值曲线和致密系数取值得到一组不同的分解分量进行对比,选取最优分量作为该阶筛分的ICC分量,从而来保障最终分解效果优于LCD方法分解效果。
对仿真信号的分析结果证实,ACD方法在提高分解结果正交性和精确性以及抑制模态混叠方面优于EMD、LCD、总体平均经验模态分解(ensemble empirical mode decomposition,EEMD)[10]方法和ACLCD方法。对具有碰摩故障的转子振动位移信号的分析结果验证了ACD的有效性,从而为旋转机械故障诊断提供了一种新的方法。
1ACD方法
1.1ACD均值曲线
对于基于筛分的自适应信号分解方法,定义合理的均值曲线是其关键所在。然而困难在于到目前为止,EMD和LCD等这类方法中均值曲线的定义都是经验性的,还没有文献给出均值曲线确切的数学定义。本文综合多种典型的数据计算方法,定义了以下5种具有代表性的均值曲线作为ACD方法的均值曲线。
(1)Hermite插值均值(Hermite interpolation mean,HIM),均值曲线由两相邻同类极值点的Hermite插值生成的曲线计算产生。
(2)Lagrange插值均值(Lagrange interpolation mean,LIM),均值曲线由3个相邻同类极值点的Lagrange插值生成的曲线计算产生。
(3)分段多项式均值(piecewise polynomial mean,PPM),均值曲线由3个相邻同类极值点的分段多项式插值生成的曲线计算产生。
(4)最小二乘均值(least squares mean,LSM),均值曲线由3个相邻同类极值点的最小二乘拟合生成的曲线计算产生。
(5)局部特征尺度均值(local characteristic-scale mean,LCM),定义参见文献[4]。
对前4种均值曲线的定义描述如下。
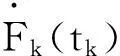
(1)Fk(tk-2)=Xk-2,Fk(tk)=Xk,Fk(tk+2)=Xk+2
(3)Fk(t)≥x(t)或Fk(t)≤x(t)
则称Fk(t)为信号x(t)在区间[tk-2,tk+2]上的局部上(下)包络线。
1.2ICC分量定义
综合多种瞬时频率具有物理意义的单分量信号定义方法[4,11-12],本文定义了一种新的单分量信号——内禀致密尺度分量(ICC)。ACD方法假设任何复杂信号x(t)(t>0)都可以被分解为有限个ICC分量与一个趋势项之和,且任何两个ICC分量之间相互独立。
ICC分量需满足以下条件:
(1)在信号x(t)(t>0)的整个数据段内,所有的极大值均为正,所有的极小值均为负(不含伪极值点),任意两个相邻的极大值和极小值之间保持严格单调性。
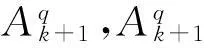
(1)
其中,Q=5,a=0.5。
(3)在每阶筛分中选取不同的均值曲线,同时改变致密系数θ的取值,得到满足条件(1)和条件(2)的分量,称之为C分量,将满足ICC分量评价准则的C分量称为该阶筛分的ICC分量。ICC分量对应的均值曲线类型,即为该阶筛分所选用的均值曲线;对应的致密系数θ的取值,称为该阶筛分的最优致密系数θopt。
条件(1)要求任意两相邻的极值点之间保持单调,是为了规避骑波的情形,保证波形单一,但该限制条件只针对增加伪极值点之前的原始信号;条件(2)是为了保证得到的每个C分量波形的光滑性和对称性;条件(3)为了保证得到的ICC分量最优。
1.3ICC分量评价准则
在ACD的每阶筛分中,为评价选取Q种不同的均值曲线,且同时改变致密系数取值得到的一组不同C分量的精确性,需建立ICC分量评价准则。由于ICC的定义是基于假设得到的C分量为近似窄带信号,根据窄带信号特性,窄带信号的带宽越小则频率的调制越小[13],因此,本文借鉴文献[14]对EMD方法改进的思路,和文献[8]对LCD方法改进的思路,采用瞬时频率波动标准差最小准则作为ICC分量的评价准则。主要计算步骤如下:
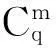
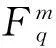
(4)求解频率波动量:
1.4ACD分解过程
(1)对实信号x(t)(t>0),致密系数θ在取值范围内,以一定步长改变,得到的一系列值记为θm。
(2)确定原始信号x(t)的所有极值点(tk,Xk),k=1,2,…,K。
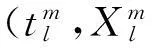
(2)
l=3,4,…,L-2
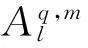
(3)
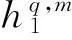
(4)
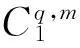
(8)将I1(t)从原始信号中分离,得到剩余信号R1(t):
R1(t)=x(t)-I1(t)
(5)
若R1(t)为常函数或单调函数,则迭代结束;否则再将R1(t)视为原始数据,重复上述步骤(1)~步骤(8),循环n次,直至Rn(t)为常函数或单调函数,依次得到ICC分量I1(t),I2(t),…,In(t)和趋势项Rn(t)。
(9)原始信号分解为n个ICC分量与一个趋势项Rn(t)之和,分解结束,即
(6)
若信号x(t)的尺度未发生混叠,在原始信号中新增伪极值点的对数为零,则致密系数的总数M值为零,此种情况ACD的分解步骤与M值为1的步骤相同。事实上,LCD和ACLCD方法,都是ACD方法的特例。
1.5仿真信号分析
为了说明所提出的ACD方法的优越性,不失一般性,考虑如下混合信号:
x(t)=x1(t)+x2(t)t∈[0,1]
(7)
其中,x1(t)为高频间歇信号,x2(t)=sin(40πt)。仿真信号x(t)的时域波形如图1所示。
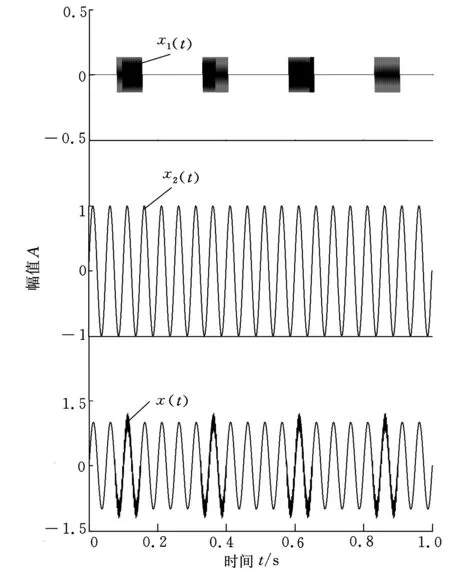
图1 仿真信号x(t)及其各成分的时域波形
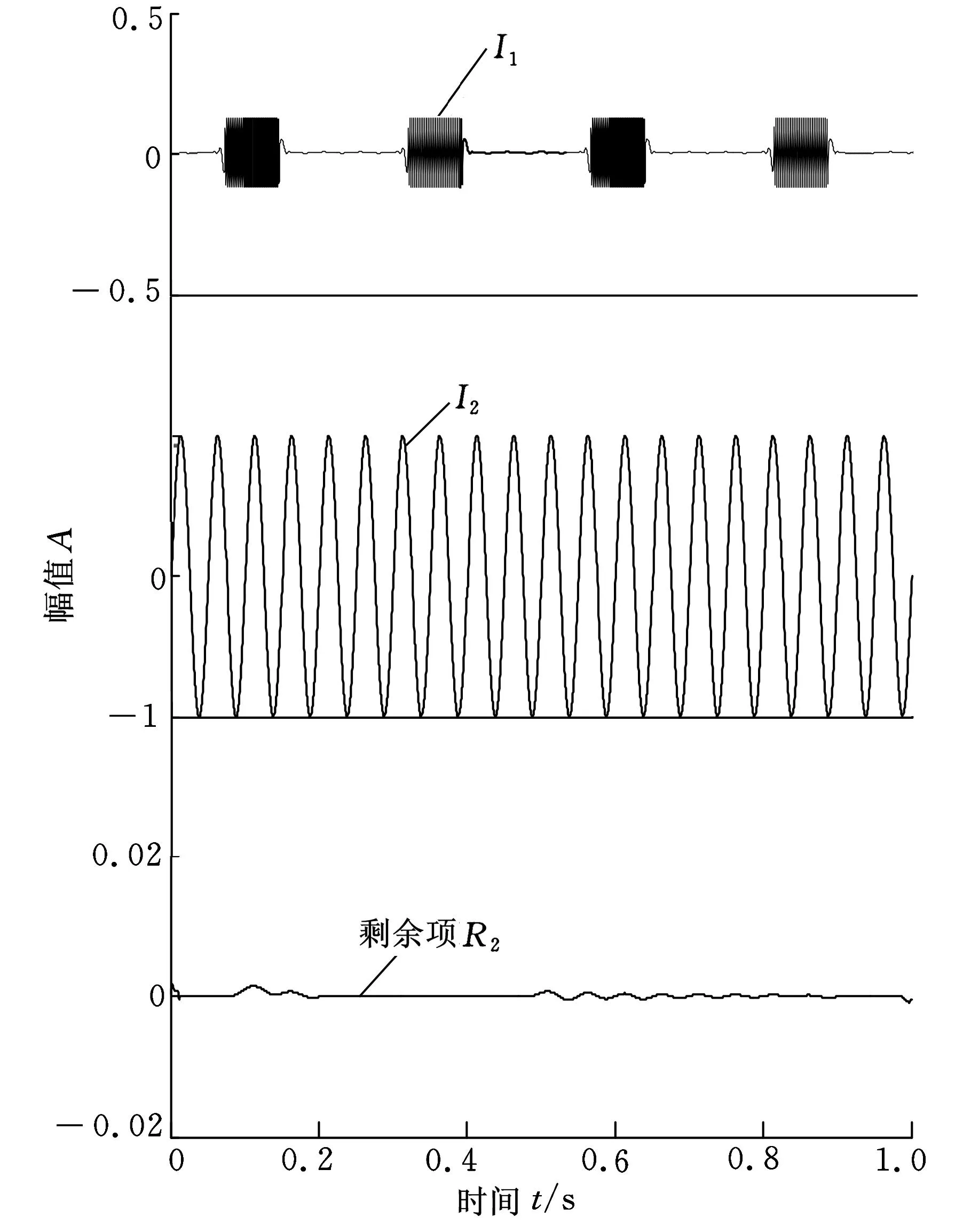
图2 仿真信号x(t)的ACD分解结果
分别采用ACD、EMD、LCD 、EEMD和ALCD 5种方法对仿真信号x(t)进行分解,分解结果分别如图2~图6所示(端点效应处理后)。其中,Iv(v=1,2,3)分别为第v个内禀尺度(ISC)分量;Cu(u=1,2,3,4)分别为第u个内禀模态函数(IMF)分量。采用EEMD方法对仿真信号x(t)进行分解时,添加0.2的噪声幅值,添加200个噪声数。5种方法的分解绝对误差如图7所示。分解绝对误差定义为:分解得到的有效分量分别与对应的仿真信号分量x1(t)和x2(t)之差的绝对值。
由图2和图7可以看出,ACD方法的分解结果比较理想,两个ICC分量与对应的仿真信号分量均非常接近,且相对于EMD、LCD、EEMD和ACLCD方法,ACD的分解绝对误差要小。
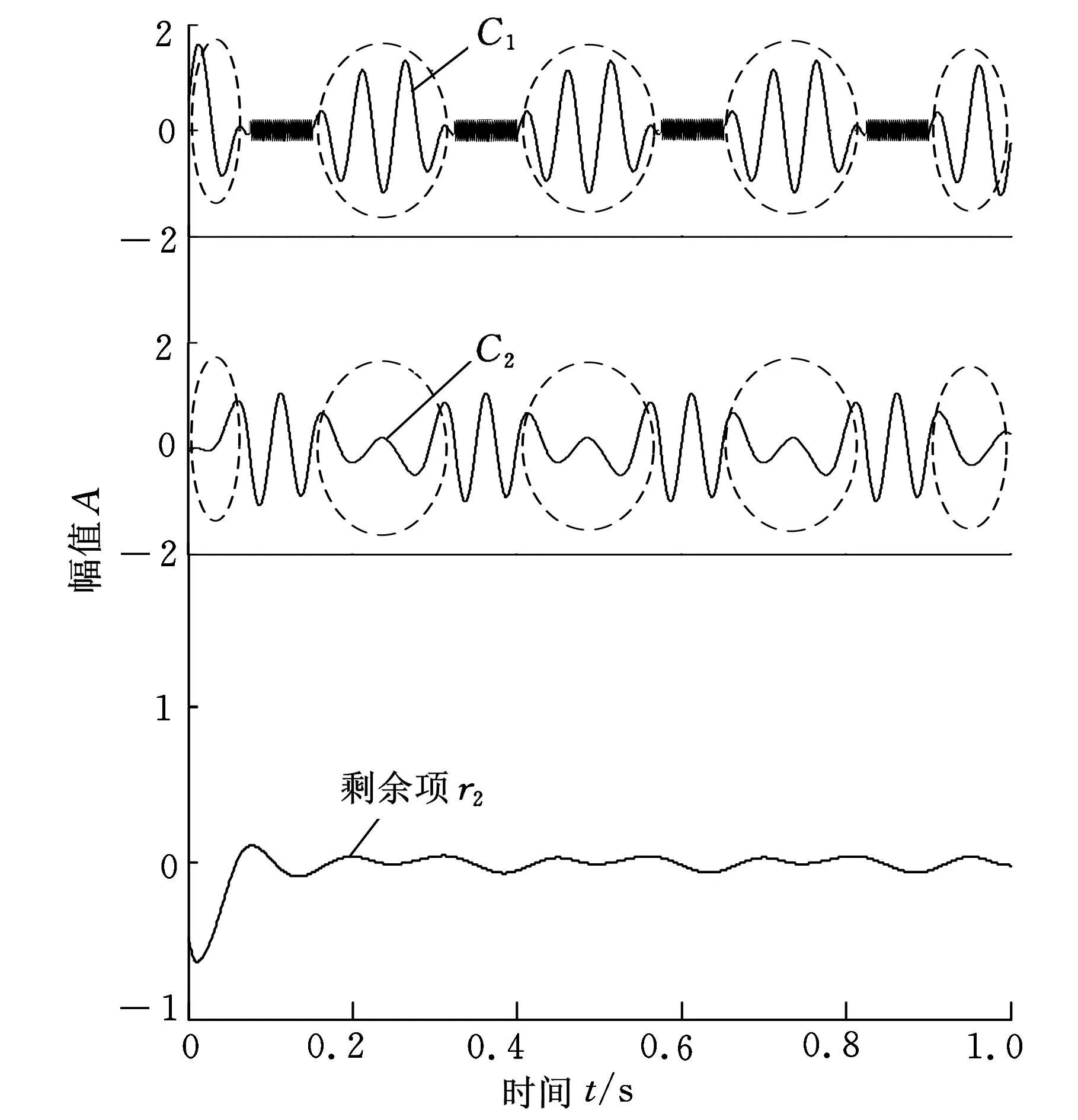
图3 仿真信号x(t)的EMD分解结果
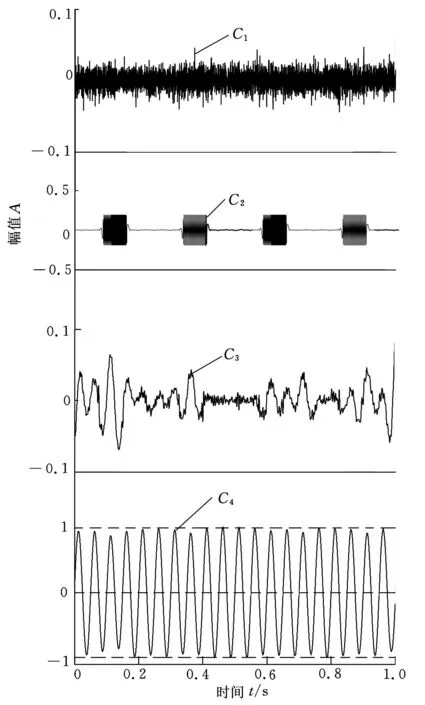
图5 仿真信号x(t)的EEMD分解结果的前四个分量
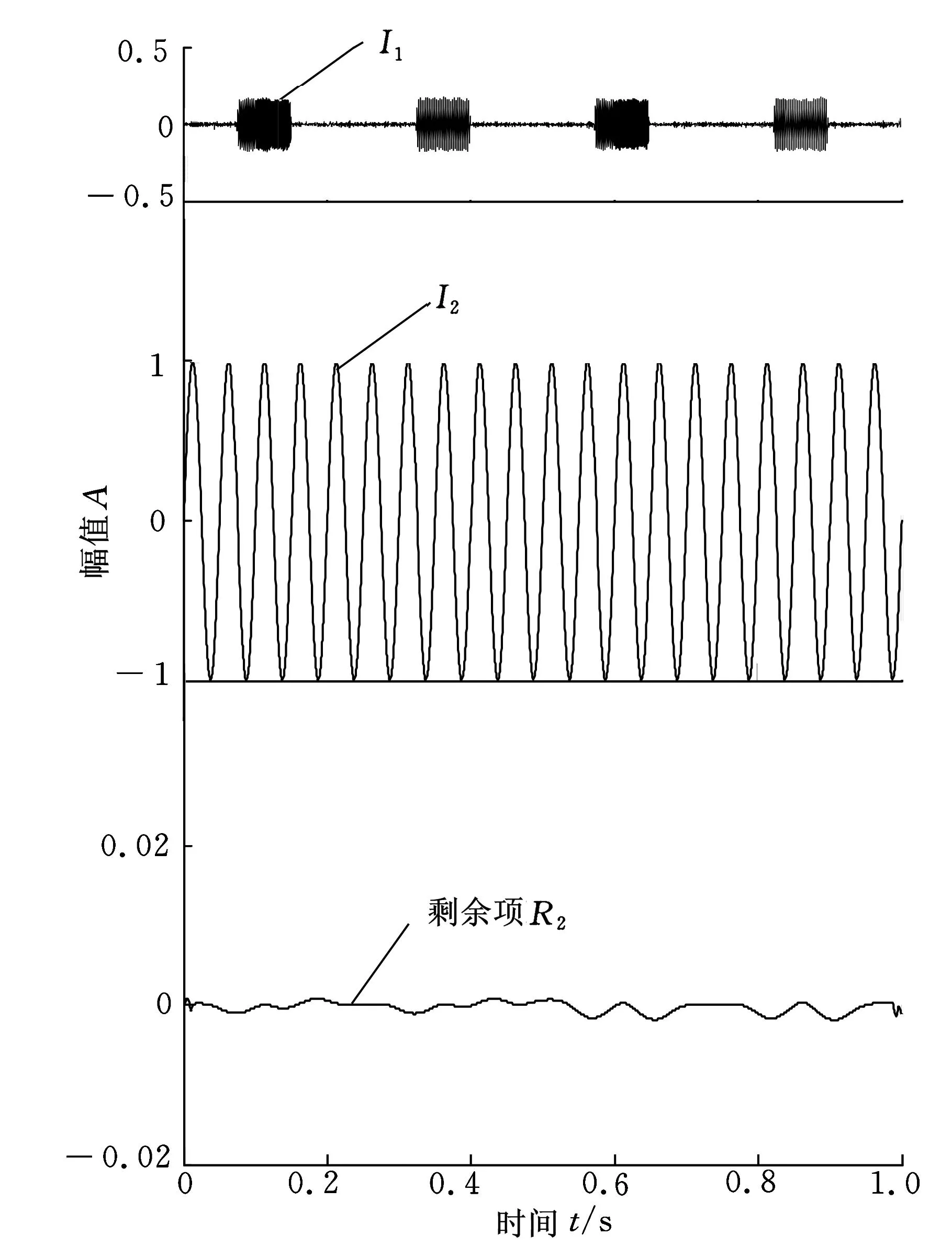
图6 仿真信号x(t)的ACLCD分解结果
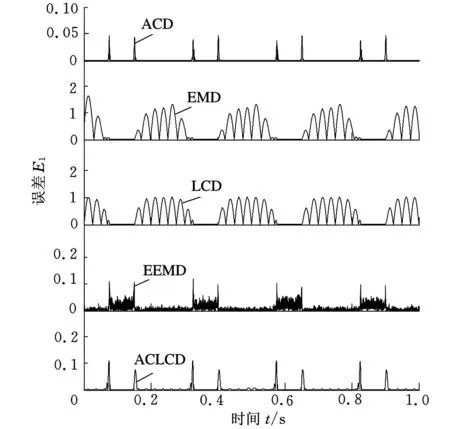
(a)5种方法得到的与x1(t)对应分解分量的分解绝对误差
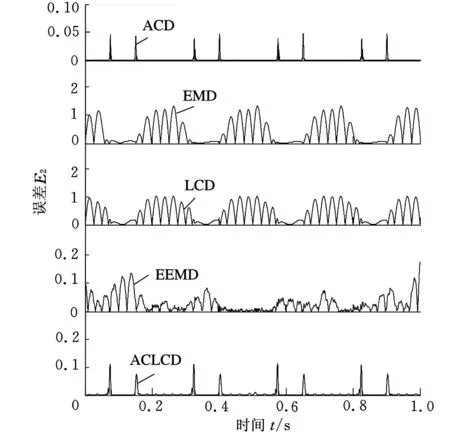
(b)5种方法得到的与x2(t)对应分解分量的分解绝对误差图7 5种方法分解仿真信号x(t)的分解绝对误差
由图3、图4和图7可以看出,EMD和LCD方法均无法有效地将幅值较小的高频间歇信号分量从仿真信号模型中分离出来,出现了模态混叠和波形失真(图3和图4中虚线所圈部分),分解绝对误差也较大。且EMD方法相对于LCD方法,无论是第一分量还是第二分量,其分解绝对误差均略大一些。
由图5和图7可以看出,EEMD方法也可以较为有效地实现对仿真信号模型x(t)的分解,分量C2和C4分别对应仿真信号分量x1(t)和x2(t),两分量分解结果也比较理想。但EEMD在分解过程中出现了一个伪分量(图5中曲线C3)。相对ACD和ACLCD方法,EEMD方法得到的两有效分解分量的分解绝对误差均略大一些。
由图6和图7可以看出,ACLCD方法也可以较为有效地实现对仿真信号模型的分解,分解分量与真实分量也非常接近。相对ACD方法,ACLCD方法得到的两分量的分解绝对误差均略大一些。
上述对比分析结果验证了ACD方法的有效性。
为进一步比较5种方法的分解效果,本文还考察了5种分解方法的分解正交性指标(index of orthogonality,IO)[11],以及5种分解方法得到的有效分解分量与其对应的真实分量之间的均方根误差(root mean square error,RMSE)和相关系数(correlation coefficient,CC)[11]。IO值越小,表示所有分解分量之间的正交性越好;RMSE值越小,表示分解误差越小;CC值越大,表示分解的准确性越高。各指标值分别如表1所示。其中Ri和Ci分别表示第i个有效分解分量与其对应的真实分量的RMSE和CC,i=1,2。
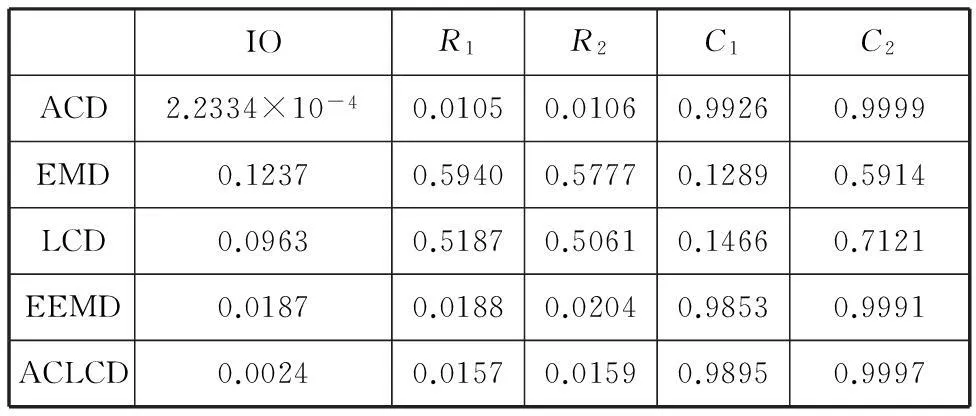
表1 5种分解方法的各指标值对比
由表1可以看出,ACD方法的IO值和RMSE值均小于EMD、LCD、EEMD和ACLCD 4种方法的IO值和RMSE值,而CC值则大于EMD、LCD、EEMD和ACLCD 4种方法的CC值。说明了与EMD、LCD、EEMD和ACLCD 4种方法相比,ACD方法在分解正交性和精确性等方面表现出一定的优越性。
2应用实例
为了进一步说明ACD方法的有效性和实用性,将其应用于具有碰摩故障的转子振动位移实验信号分析中。实验装置示意图见图8。转子转速为3000 r/min,转频fr=50 Hz,实验采样频率为fs=2048 Hz,采样时长为0.5 s。实验数据的时域波形如图9所示,其幅值谱如图10所示。转子产生碰摩故障时,其振动位移信号会产生一个以转频fr为调制频率的高频碰摩分量[15]。由图9可以看出高频碰摩分量非常微弱,被淹没在强大的背景信号中,图10中看到的主要频率成分是转频fr及其3倍频,无法准确判断实验数据的故障类型。
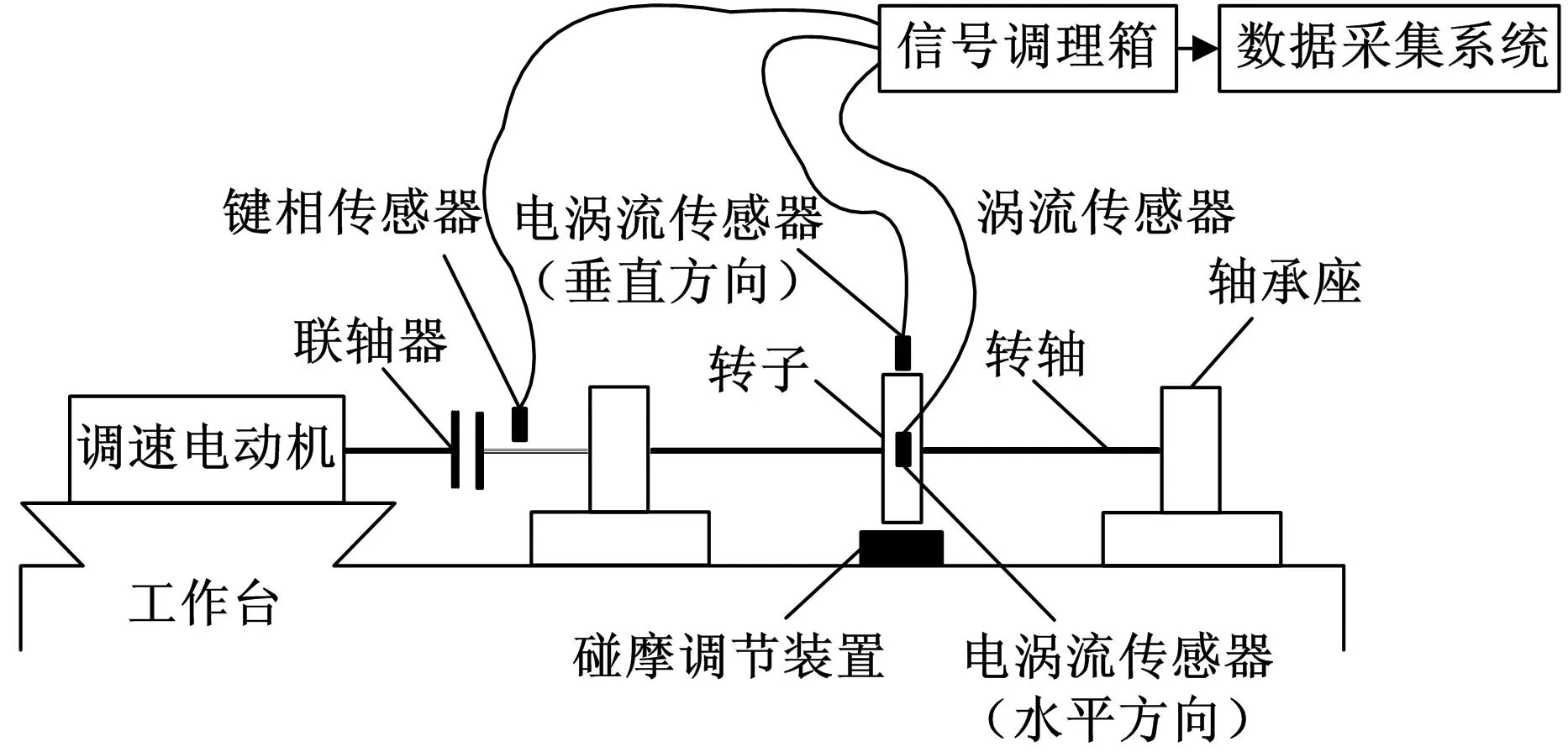
图8 转子实验装置示意图
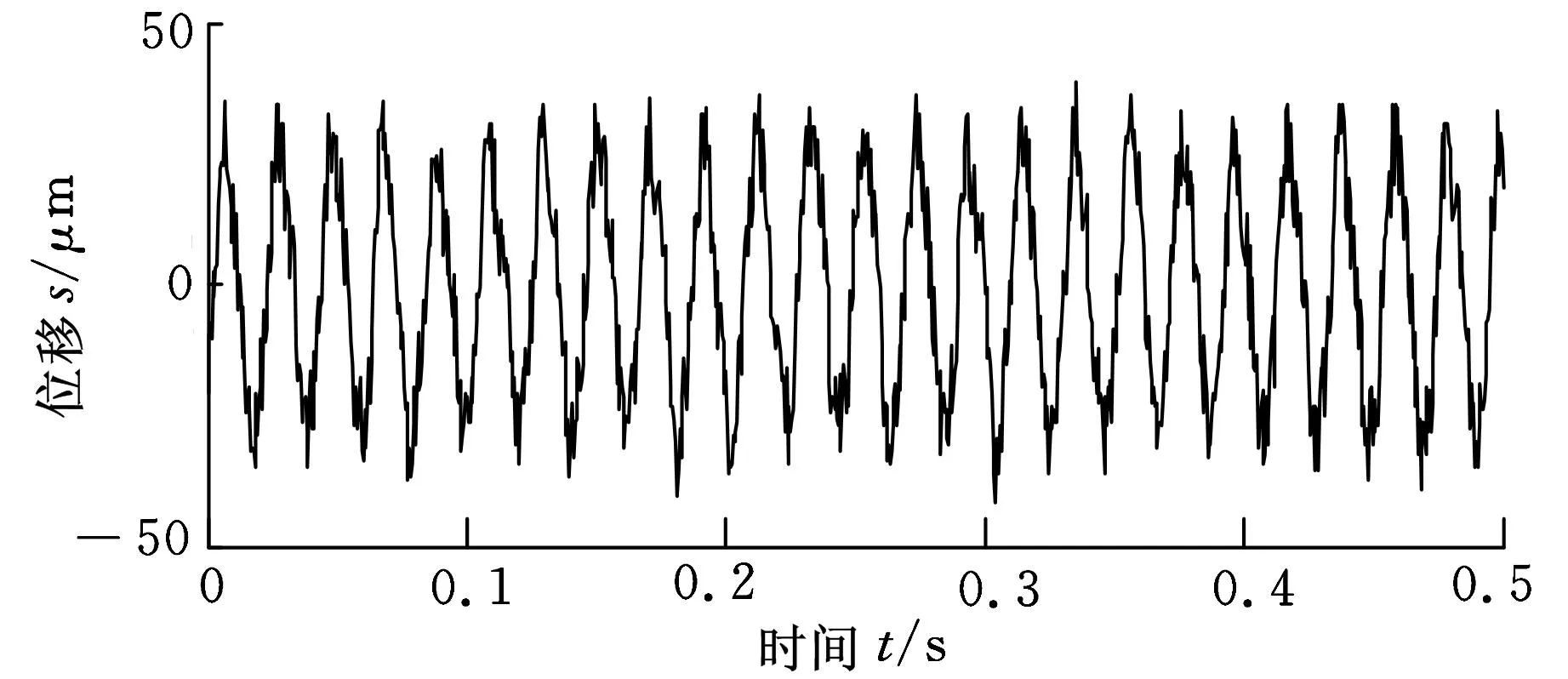
图9 转子碰摩故障实验数据的时域波形
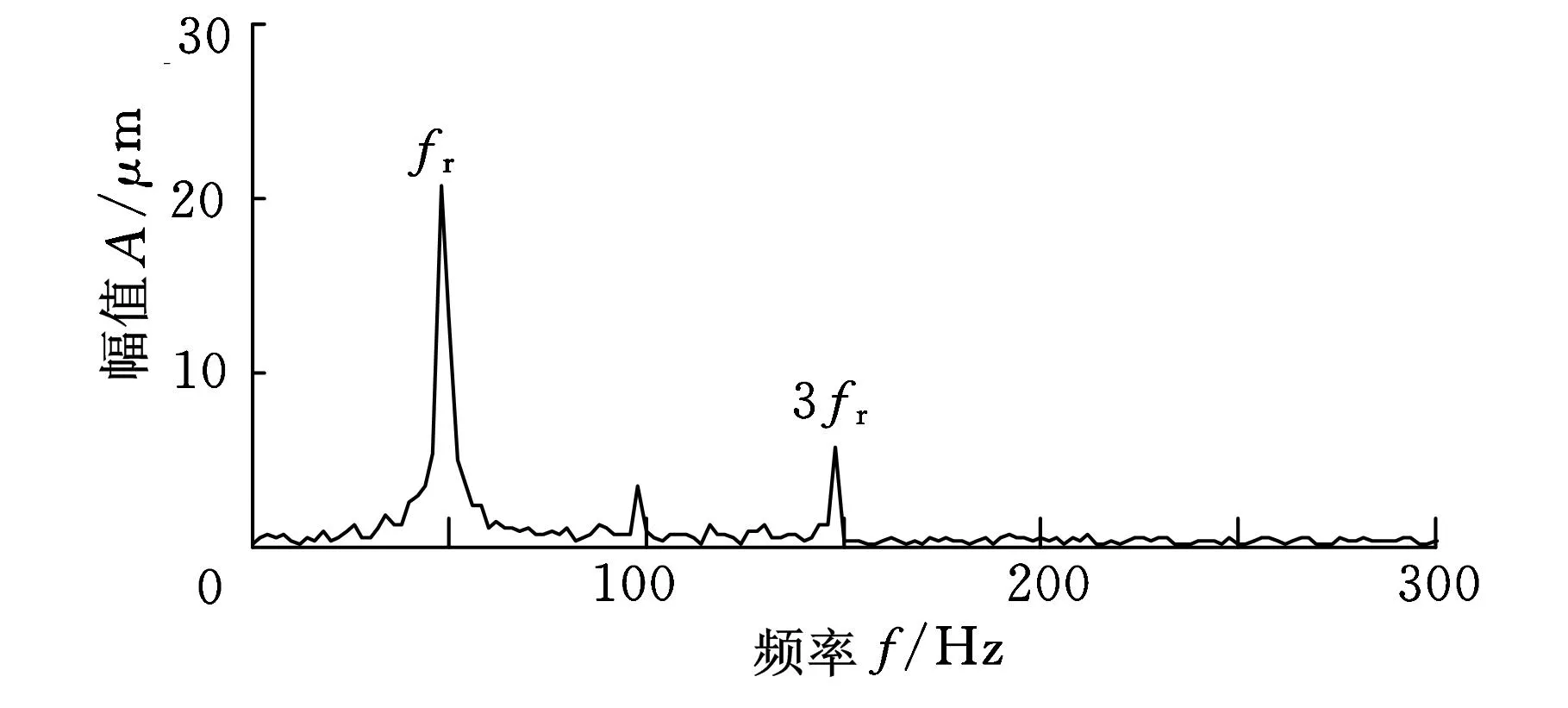
图10 转子碰摩故障实验数据的幅值谱
为提取高频碰摩信息,采用ACD方法对实验数据进行分解,分解结果如图11所示。
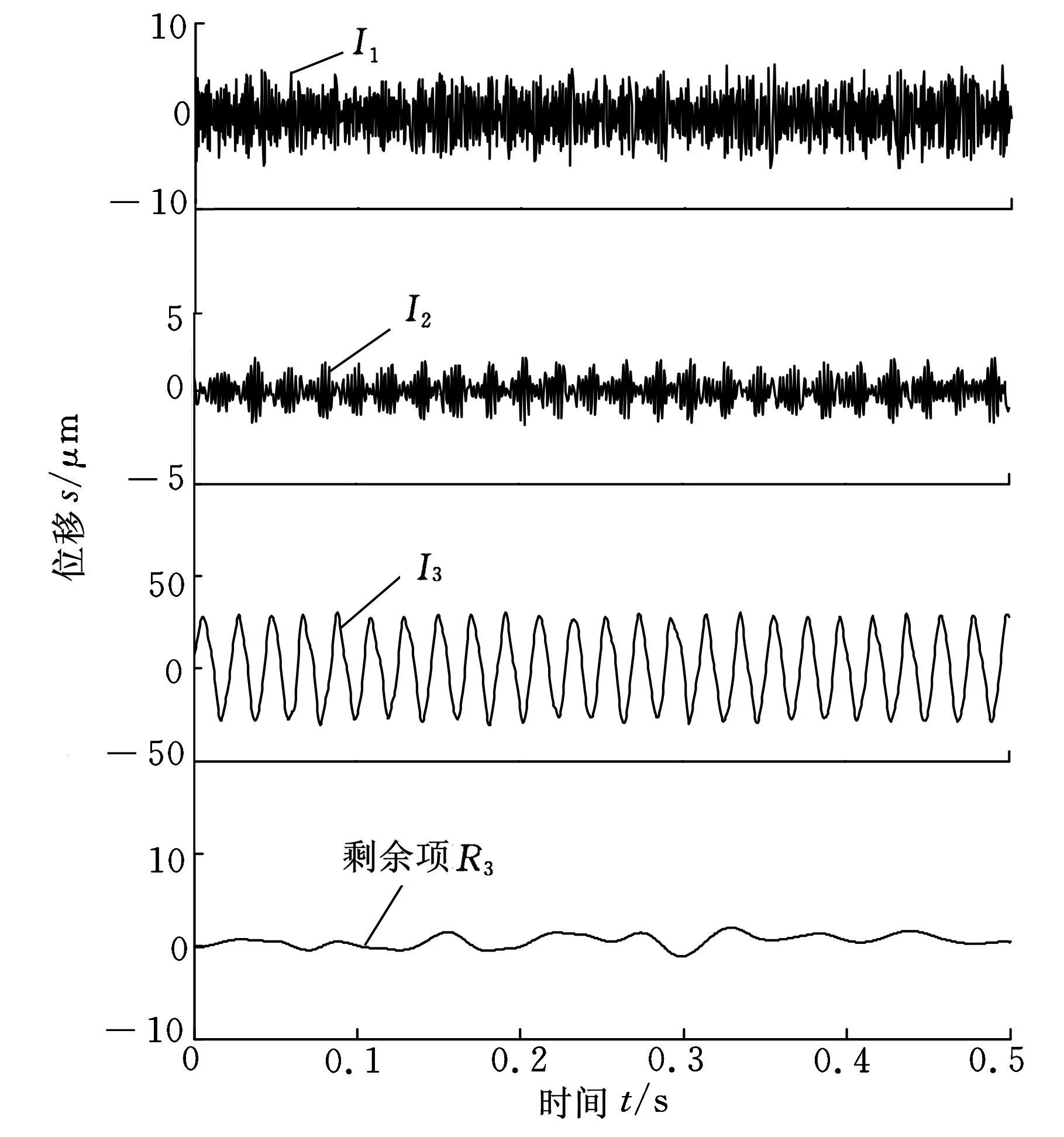
图11 转子碰摩故障实验数据的ACD分解结果
对图11所示的ACD方法对转子碰摩故障实验数据的分解结果进行分析,分量I1是高频噪声信号;分量I2具有明显的调制特征,包含了主要故障信息;分量I3是与转频相关的背景信号。由图12所示的ACD分量I2的包络谱图可以看到明显的转频fr及其2倍频成分,说明分量I2的调制波频率与转频fr相同,这是由于转子每旋转一周动件与静件摩擦一次造成的[16]。因此分量I2的主要成分是碰摩故障信号,当然也包含了一些噪声。这验证了ACD在实验数据分解时,可将其他干扰频率成分分解到其他分量里面;干扰频率成分得到了有效滤除,使得实验数据所包含的故障特征信息凸显出来。ACD方法可有效应用于具有碰摩故障的转子故障诊断中。
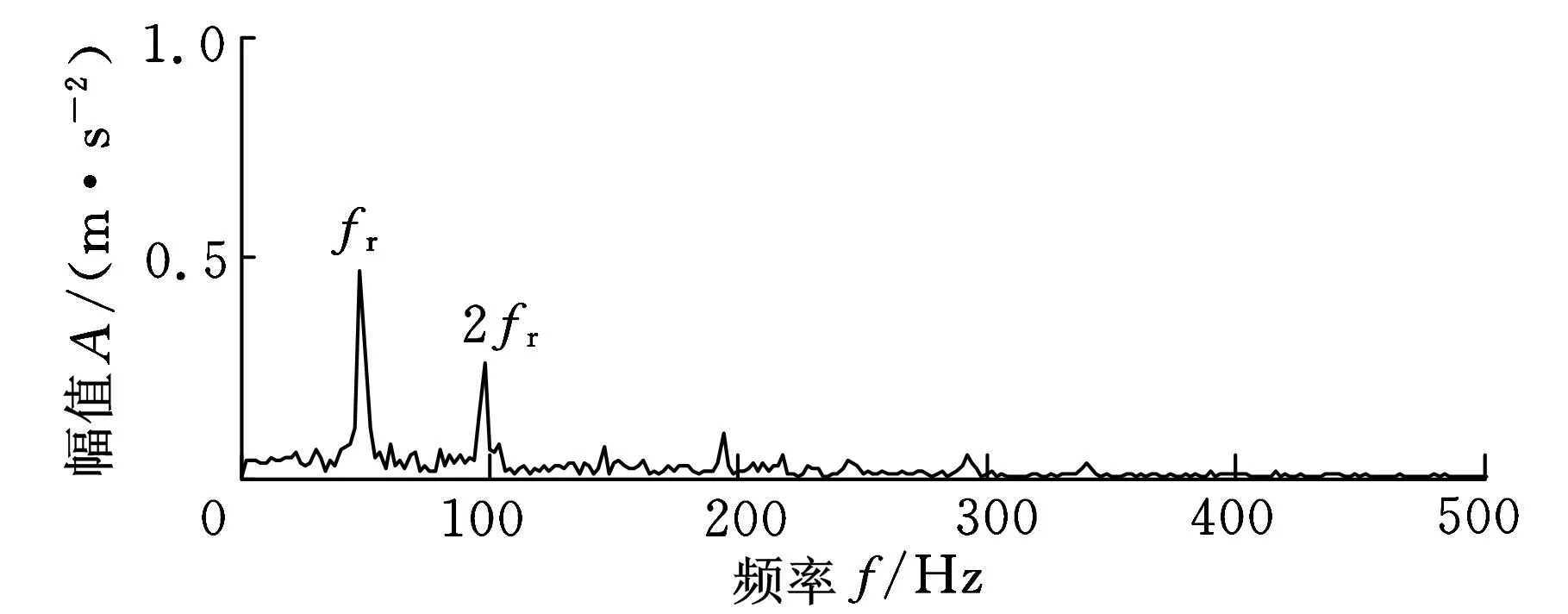
图12 ACD的分量I2的包络谱
同时,采用LCD方法对实验数据进行分解,结果如图13所示。由图13可以看出,采用LCD方法对实验数据分解得到的分量I1也是高频噪声信号;分量I2和分量I3是与转频相关的背景信号,但均看不出调制特征;且分量I2和分量I3出现了严重的波形失真和模态混叠(图13中虚线所圈部分)。这是因为采用LCD对实验数据进行分解时,无法有效地将幅值较小的碰摩故障分量与噪声信号和转频背景信号分离,出现了模态混叠和波形失真,未能有效识别实验数据所包含的故障类型。
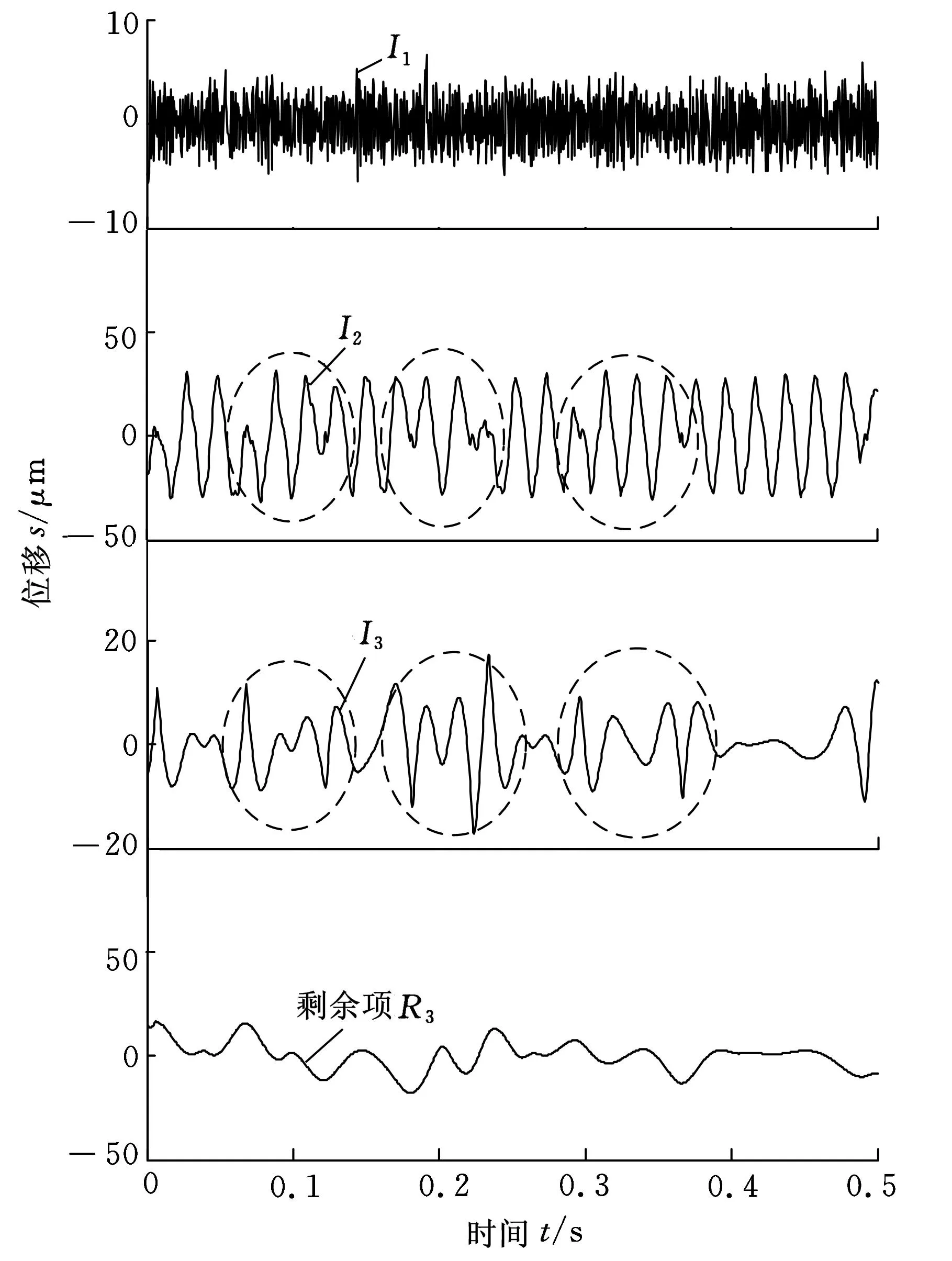
图13 转子碰摩故障实验数据的LCD分解结果
上述实验数据分析说明,相对LCD方法,ACD方法能更为有效地将故障信号分量从强大的背景信号中提取出来,实现故障信号、背景信号和噪声信号的分离,从而实现转子碰摩故障诊断。
3结论
(1)对仿真信号的分析结果证实,ACD方法在提高分解结果正交性和精确性,以及抑制模态混叠方面要优于EMD、LCD、EEMD和ACLCD方法。
(2)对实验数据的分析结果验证了ACD方法的有效性,从而为旋转机械故障诊断提供了一种新的方法。
(3)ACD方法不需要预设置运行参数,规避了EEMD这类噪声辅助的数据分析方法中主要参数由人为经验确定、缺乏自适应性的不足,是一种有效的自适应信号分解方法。
(4)本文提出的ACD方法,在注重定义均值曲线以提高分解精度和有效性的同时,也注重对原始信号的极值尺度进行细化以提升其抑制模态混叠的能力,这为研究基于筛分的自适应时频分析方法提供了一种新的思路。
参考文献:
[1]Hong H,Liang M.Fault Severity Assessment for Rolling Element Bearings Using the Lempel-Ziv Complexity and Continuous Wavelet Transform[J].Journal of Sound and Vibration,2009,320(1/2):452-468.
[2]曹冲锋,杨世锡,杨将新.一种抑制EMD端点效应新方法及其在信号特征提取中的应用[J].振动工程学报,2008,21(6):588-593.
Cao Chongfeng, Yang Shixi, Yang Jiangxin. A New Method for Restraining the End Effect of Empirical Mode Decomposition and Its Applications to Signal Feature Extraction[J]. Journal of Vibration Engineering,2008,21(6):588-593.
[3]Yang Yu,Cheng Junsheng,Zhang Kang.An Ensemble Local Means Decomposition Method and Its Application to Local Rub-impact Fault Diagnosis of the Rotor Systems[J].Measurement,2012,45(3):561-570.
[4]程军圣, 郑近德, 杨宇. 一种新的非平稳信号处理方法——局部特征尺度分解法[J]. 振动工程学报, 2012, 25(2): 215-220.
Cheng Junsheng, Zheng Jinde, Yang Yu. A Nonstationary Signal Analysis Approach:the Local Characteristic-scale Decomposition Method[J]. Journal of Vibration Engineering, 2012, 25(2):215-220.
[5]Zheng Jinde, Cheng Junsheng,Yang Yu.A Rolling Bearing Fault Diagnosis Approach Based on LCD and Fuzzy Entropy[J]. Mechanism and Machine Theory,2013,70:441-453.
[6]郑超,郭奇,郭丽杰,等.基于局部特征尺度分解的旋转机械故障欠定盲源分离方法研究[J].燕山大学学报,2014,38(2):168-174.
Zheng Chao, Guo Qi, Guo Lijie, et al.Underdetermined Blind Source Separation Method of Rotating Machinery Faults based on Local Characteristic-scale Decomposition[J]. Journal of Yanshan University,2014,38(2):168-174.
[7]郑近德, 程军圣, 杨宇. 部分集成局部特征尺度分解: 一种新的基于噪声辅助数据分析方法[J].电子学报,2013,41(5):1030-1035.
Zheng Jinde, Cheng Junsheng, Yang Yu. Partly Ensemble Local Characteristic-scale Decomposition:a New Noise Assisted Data Analysis Method[J]. Acta Electronica Sinica, 2013, 41(5): 1030-1035.
[8]吴占涛, 程军圣, 李宝庆, 等. 自主致密局部特征尺度分解方法及其应用[J]. 中国机械工程,2015,26(11):1464-1470.
Wu Zhantao, Cheng Junsheng, Li Baoqing, et al. Method of Autonomous Compact Local Characteristic-scale Decomposition and Its Applications[J]. China Mechanical Engineering, 2015, 26(11): 1464-1470.
[9]Zheng Jinde, Cheng Junsheng, Yang Yu. Generalized Empirical Mode Decomposition and Its Applications to Rolling Element Bearing Fault Diagnosis[J]. Mechanical Systems and Signal Processing, 2013, 40(1):136-153.
[10]Wu Zhaohua, Huang N E. Ensemble Empirical Mode Decomposition: a Noise-assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.
[11]Huang N E, Shen Zheng, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,1998,454(1971):903-995.
[12]Smith J S. The Local Mean Decomposition and Its Application to EEG Perception Data[J]. Journal of the Royal Society Interface,2005,2(5):443-454.
[13]Rilling G, Flandrin P, Goncalvés P.On Empirical Mode Decomposition and Its Algorithms[C]//IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing. Grado, 2003:1-5.
[14]郑近德, 程军圣. 改进的希尔伯特-黄变换及其在滚动轴承故障诊断中的应用[J]. 机械工程学报,2015,51(1):138-145.
Zheng Jinde, Cheng Junsheng. Improved Hilbert-Huang Transform and Its Applications to Rolling Bearing Fault Diagnosis[J]. Journal of Mechanical Engineering, 2015, 51(1): 138-145.
[15]马辉, 陈雪莲, 滕云楠, 等. 转子系统碰摩故障分岔特性的实验研究[J]. 仪器仪表学报,2009,30(9):1808-1812.
Ma Hui, Chen Xuelian, Teng Yunnan, et al. ExperimentalResearch on Bifurcation Characteristics of Rotor System with Rub-impact Fault[J]. Chinese Journal of Scientific Instrument, 2009, 30(9): 1808-1812.
[16]陈向民, 于德介, 罗洁思. 基于信号共振稀疏分解的转子早期碰摩故障诊断方法[J]. 中国机械工程, 2013, 24(1): 35-41.
Chen Xiangmin, Yu Dejie, Luo Jiesi. Early Rub-impact Diagnosis of Rotors by Using Resonance-based Sparse Signal Decomposition[J]. China Mechanical, 2013, 24(1):35-41.
(编辑王艳丽)
Adaptive Characteristic-scale Decomposition Method and Its Applications
Wu ZhantaoCheng JunshengYang Yu
State key Laboratory of Advanced Design and Manufacture for Vehicle Body,
Hunan University,Changsha,410082
Abstract:Based on the research of LCD, this paper borrowed ideas from the sifting based signal decomposition methods such as EMD and LCD,and then presented a new mono-component signal with physically meaningful instantaneous frequencies, i.e.,ICC,for restraining the mode mixing problem of LCD and improving the deficiency in terms of the mean curve definition. Finally, a new signal decomposition method,ACD was proposed.Meanwhile, the evaluation criterion of ICC was also given.In the sifting procedure for separating certain order components,a set of ICCs was obtained by using different mean curves and compact coefficients. The optimal ICC for this order sifting would be selected from the candidate ICCs using the evaluation criterion of ICC, which guaranteed ACD outperforms LCD.The simulation results indicate that the decomposition effect of ACD is better than that of EMD,LCD,ensemble empirical mode decomposition(EEMD) and autonomous compact local characteristic-scale decomposition(ACLCD), experimental results of the experimental signals show its validity.Thus a new way for fault diagnosis of rotating machinery is provided.
Key words:adaptive characteristic-scale decomposition(ACD);local characteristic-scale decomposition(LCD);empirical mode decomposition(EMD);intrinsic compact-scale component(ICC);fault diagnosis
基金项目:国家自然科学基金资助项目(51375152);湖南省科技计划资助项目(2014WK3005)
收稿日期:2015-07-08
中图分类号:TH165;TH911.7DOI:10.3969/j.issn.1004-132X.2015.23.012
作者简介:吴占涛,男,1982年生。湖南大学机械与运载工程学院博士研究生。主要研究方向为动态信号处理及机械设备故障诊断。程军圣(通信作者),男,1968年生。湖南大学机械与运载工程学院教授、博士研究生导师。杨宇,女,1971年生。湖南大学机械与运载工程学院教授、博士研究生导师。
