VaR模型及其在创业投资风险管理中的应用——基于创业板指数的实证研究

叶　金，谷秀娟

(1.民生银行 郑州心怡路支行,河南 郑州 450004;2.河南工业大学 经济贸易学院,河南 郑州 450001 )



VaR模型及其在创业投资风险管理中的应用
——基于创业板指数的实证研究

叶金1，谷秀娟2

(1.民生银行 郑州心怡路支行,河南 郑州 450004;2.河南工业大学 经济贸易学院,河南 郑州 450001 )

摘要：创业投资运作过程中面临的风险问题要求其对风险进行测量与评估。选取2014年1月1日至2014年12月31日我国创业板指数日收益率和股票收盘价格作为样本,对其进行实证研究，建立VaR模型来测量其风险。实证结果表明：目前我国高新技术企业和中小企业的股票价格波动较大，风险较高，创业投资机构面临的风险比较高。只有反复和分阶段地去评价投资对象，在投资过程中采取组合投资、投资后监管和增值管理等，才能分散和控制风险。

关键词：创业投资; VaR模型; 风险控制

0引言

随着我国金融开放程度的逐步放宽，创业投资机构的发展步伐也不断加快，金融市场日趋多元化。创新型和高新技术企业的股票市场价格波动也变得更加频繁，波动幅度不断加大，创业投资的稳健经营进一步面临风险的挑战。

对于创业投资来讲，最重要的是如何运用一套科学的评估方法去选择投资项目；它的评估方法与传统的商业银行对货款的评估有着较大的不同。经过很多年的发展，传统项目的评估具备了一套较完善的评价指标和方法，创业投资的项目评估由于起步较晚，且创业投资项目大多是尚未开发的高新科技领域，项目是即将成立的新兴公司，没有过去的经营业绩可供参考；即使是经营了较长时间的公司，其技术具有独创性和新颖性，也没有同类技术的公司与之相比较。时至今日还未形成一套统一的项目评估方法。每个创业投资公司都有各自的方法，虽然这些方法各有所长，但也有待规范。因而，创业投资需要一种较为成熟的测量风险的方法去防控风险。

本文较为全面地分析了VaR模型的优缺点，认为VaR法可以在测度范围、测度工具和测度精度等方面都具有较好的优势，准确地计量创业投资的风险价值，对我国创业投资风险管理具有良好的现实意义。

1文献综述

Risk Metrics风险控制模型将VaR (Value at Risk)方法作为度量市场风险的主流方法，逐渐被众多金融机构所采用。Dimitrakopou-losI(2012)利用VaR模型将新兴的市场和发达的市场之间的股票投资进行组合投资，进一步研究了投资组合以及风险的量化问题，并在国际上推广。[1]He、Lai等(2011)利用模型对原油市场波动性进行了相关探索研究，结果表明：时域和频域的准确性，对于估计价格的稳定和波动性具有现实意义，同时，多样化的投资组合可以降低组合的风险。[3]Stavroyiannis(2011)通过VaR模型研究了富时指数，道琼斯工业平均指数，纳斯达克综合指数的历史风险值。[1]Hung等(2006)在寻求套期保值策略时，区分上方收益和下方损失，率先进行VaR框架下的套期保值比率研究，但这种套期保值策略是静态的，而大多数最小方差套期保值比率研究显示，静态策略不如动态策略有效。[4]杨杨和徐文彬(2013)选取101组上证综合指数等数据，用历史模拟法、方差-协方差法和蒙特卡罗模拟法，对风险价值进行估算。用三种方法估算的VaR值表明:在样本数据服从正态分布的条件下，三种计算方法均能得出可靠的风险值，且运用风险值所做的预测能够较好地拟合实际值。[5]李汶华等(2013)运用区间分析股票投资组合的VaR计算，研究区间分析在VaR计算方法中的应用，给出基于区间分析估计分布函数的计算步骤，将区间分析运用到VaR的计算中，以两只股票的投资组合为例得出收益率的累计概率分布，从中得到某一置信度下的VaR值，最后与蒙特卡洛模拟方法做了比较研究。研究表明，基于区间分析的VaR计算方法的运算精度和计算速度明显优于蒙特卡洛模拟方法。[6]杨夫立(2012)基于GARCH模型，研究了对数收益率时间序列在正态、t和广义误差。研究结果表明，基于GED分布的GARCH模型计算的VaR值最能真实地反映基金风险。[7]尉轶昊和毛宏(2011)通过建立期望效用-VaR模型，借助于Matlab和Monte Carlo模拟技术，深入探讨和分析了以VaR作为风险测度标准及约束时，拥有不同风险偏好及初始财富值的投资者在进行投资决策时对最优投资组合的理性选择，讨论了在中国资本市场中运用投资组合理论分散风险、稳定收益的可行性。[8]王春红等(2007)通过建立不同分布假设下GARCH族模型的VaR度量方法对银行业的同业拆借市场的利率风险进行了度量，采用Kupiec方法对模型进行了检验。研究表明，t分布并不完全适合银行业间的同业拆借利率序列的分布情况，GED分布则能较好描绘出我国银行间同业拆借利率序列的分布，而且同业拆借利率序列的杠杆效应也并不是很明确。[9]

国内外对VaR法的研究主要表现在：将VaR 用于创业投资的风险测量中的较少，VaR模型可以用来测量风险的大小，也可计算事前风险，不同于大多数风险管理方法在事后衡量风险大小，VaR法不仅可以测量单个金融工具的风险，还可用于测量投资组合风险。

2实证研究

2.1变量和样本的相关检验

创业投资企业投资过程中面临的对象主要是中小企业和高新技术企业，因此样本选取的是2014年1月1日至2014年12月31日的创业板指数中的股票收盘价格和日收益率，数据来源于锐思数据库，计量经济学软件运用的是eviews6.0版本，选取创业板指数作为样本分析股票收益率的波动性和面临的风险具有较好的分析意义。

表1　样本变量ADF检验

根据ADF检验结果得出，t统计量为-9.955788，小于在1%、5%、10%显著性水平下的临界值，因此可以拒绝原假设时间序列存在不平稳的单位根，可确定为平稳的时间序列，创业板指数日对数收益率符合平稳性假设。正态性变量的假设是否正确，将对分析结果的可靠性造成重要的影响，可利用Q-Q图检验法或者偏锋度检验法等进行检验。

2.2Q-Q图检验

我们使用Q-Q图检验可以直观地看出收益率序列的实际分布与正态分布的离散度，当散点的分布和分布的正态直线相互接近时，收益率序列符合正态分布(见图1)。

从图1中可以看出，创业板指数收益率序列的分布并不完全与正态分布相互接近，而且出现了向后尾以及左偏的现象，因此收益率不符合正态分布。

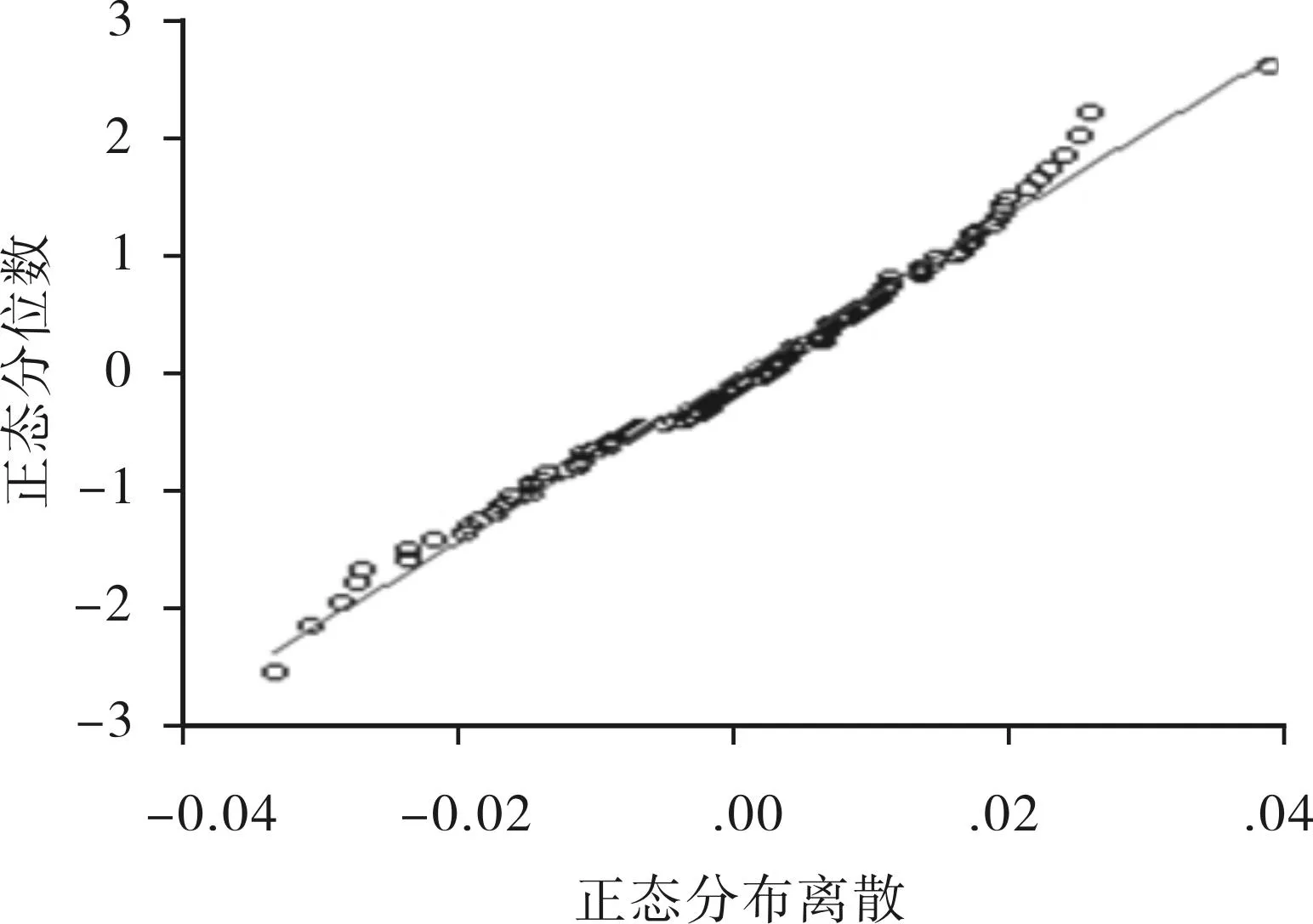
图1　创业板指数日对数收益率正态　分布Q-Q图检验

2.3偏锋度检验

偏锋度的检验也是检验正态分布的步骤之一，通过变量分布的统计量以及直方图、偏度和峰值来检测是否符合正态性分布。通常情况下，正态分布的偏度(skewness)为0，峰度(kurtosis)为3(见图2)。

如图2所示，偏度值为-0.650342，小于0则为负偏，左尾偏长，右侧分布较为集中，所以收益的可能大于损失；峰值为3.833182大于3为尖峰，证明在极端的事件下的收益率较远偏离均值，促使收益分布出现“厚尾”现象。除此之外，JB的统计量为10.53805，相伴概率接近为0，拒绝收益率服从分布正态。综上所述，创业板收益率序列指数并不服从正态分布，显示出非对称的尖峰厚尾的情况，因此需要我们进一步寻找其他合适的分布拟合实际数据。

2.4自相关性检验

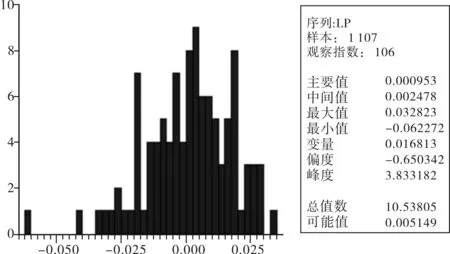
图2　创业板指数日对数收益直方图

在时间序列的数据处理过程中，需要对自相关性进行检测。根据序列的自相关系数(AC)和偏自相关系数(PAC)来测定，确定回归项(AR)和移动平均项(MA)的阶数，计算出均值方程(见图3)。

根据图3所示，收益率的自相关系数和偏自相关系数接近0，且Q值统计量小于一定水平下的临界值，明显大于相应的显著水平，证明模型无法拒绝自相关性不存在的原假设，创业板指数的收益率对数序列是随机的，不存在自相关性。得出中小板指数收益序列的均值方程:

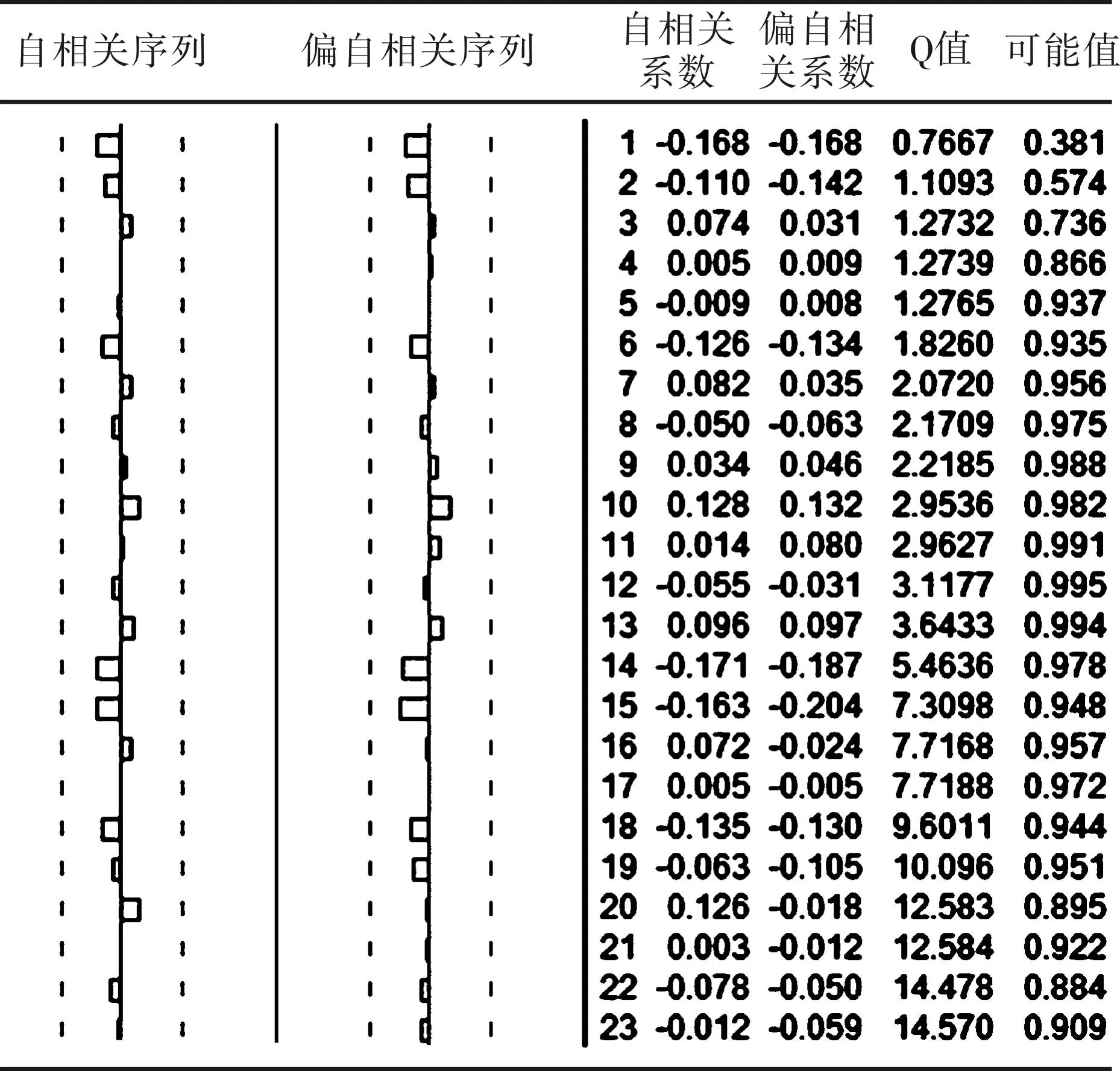
图3　创业板指数日对数收益率自相关图

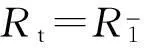
①

其中，Rt为对数收益率均值，Ut为模型的随机误差项。

2.5异方差性检验

计量经济学中，随机误差项是服从方差，而针对股价和收益率、通货膨胀率和汇率的时间序列预测研究发现，不同时期这些变量会有不同的变化，预测会变得更加的精确，同时具有聚集、突发和时变性。这种变化是由于受到国际资金流动、政府财政与货币政策以及投资者心理预期多种影响。由此可见，某一固定的常数不一定符合随机误差项的条件方差，随着时间的变化，对于时间序列的异方差性，可以采用ARCH-LM检验以及残差平方图来检验。对①式的残差做出分布图(见图4)。

从图4可以看出，均值方程的残差的波动呈现出“成群”现象，在一些分隔的时间段内波动较小，如横轴刻度之间的振幅为±0.03;而在另一些时期里波动较大，横轴上振幅达到甚并超过±0.05，这说明随机误差项具有异方差性。

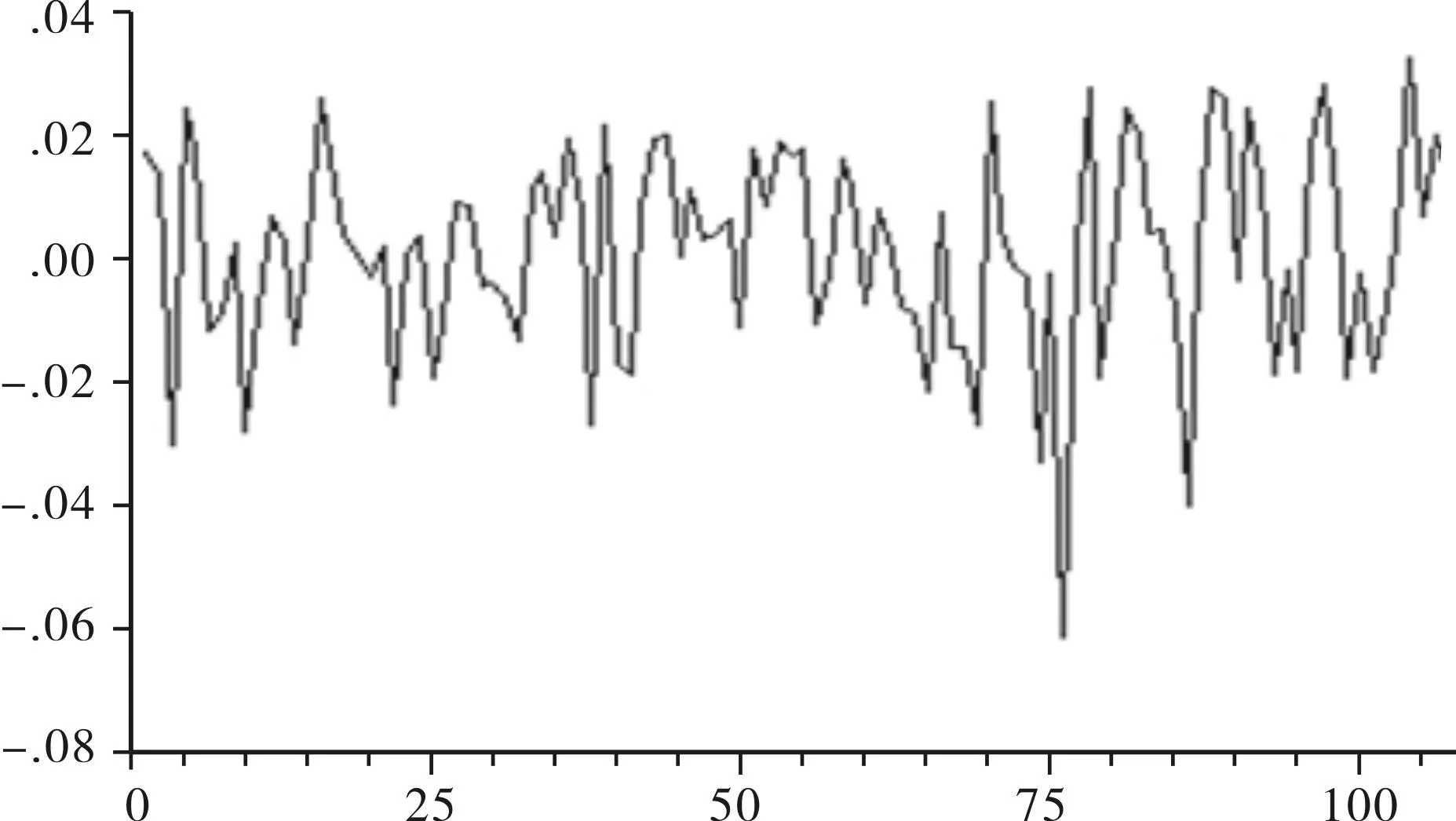
图4　创业板指数日对数收益率序列残差分布图

2.6对残差平方的自相关系数和偏自相关系数检验

从图5自相关系数和偏相关系数的检验可以看出:除了一阶滞后期不存在ARCH效应，其他滞后期系数都不是0，且Q统计量显著，伴随概率小，所以得出结论:原均值方程的残差序列存在着较为突出的ARCH效应，即具有条件异方差性。

3模型建立和实证分析

通过检验后，可以采用历史模拟法和方差-协方差法来估计VaR值。历史模拟法按照历史的数据得到历史收益率的分布，再依照置信水平得到VaR的估计值；协方差法则需要先估计时间序列的波动率，即条件标准差，再利用公式VaRt=Wt-1∂cσt 来计算VaR值其中Wt-1是t-1期创业投资企业持有的隔夜拆解头寸，∂c是相应假设分布显著性水平为c的分位数，本文假定每日的隔夜拆借头寸都为1，则VaRt=∂cσt。为了计算VaR值，需要动态地计算每天承担的市场风险。表2中显示了VaR模型估计每日动态VaR值与收益率序列的比较。而历史模拟法、Delta-正态法、指数加权法等对收益率波动反应比较迟钝；另外，模型能很好地覆盖收益率波动风险。收益率序列某些时点突破了当日动态VaR值，这些突破点称为例外值点，动态VaR值小于日收益率损失的点称为例外值点，因此统计了 90%、95%、99%置信水平下，各模型的实际例外值个数。

从表2中可以看出，95%和90%的置信水平下，估计的理论突破次数都大于实际突破次数，说明模型中存在高估利润的情况；在99%的置信水平下，估计理论突破次数大于实际突破次数。利用实际以及理论突破次数比较，只可以大致估计模型的结果，至于相差多大，如何分布例外值点才是重要的，再判断VaR模型的有效性。

图5　收益率序列残差平方相关图

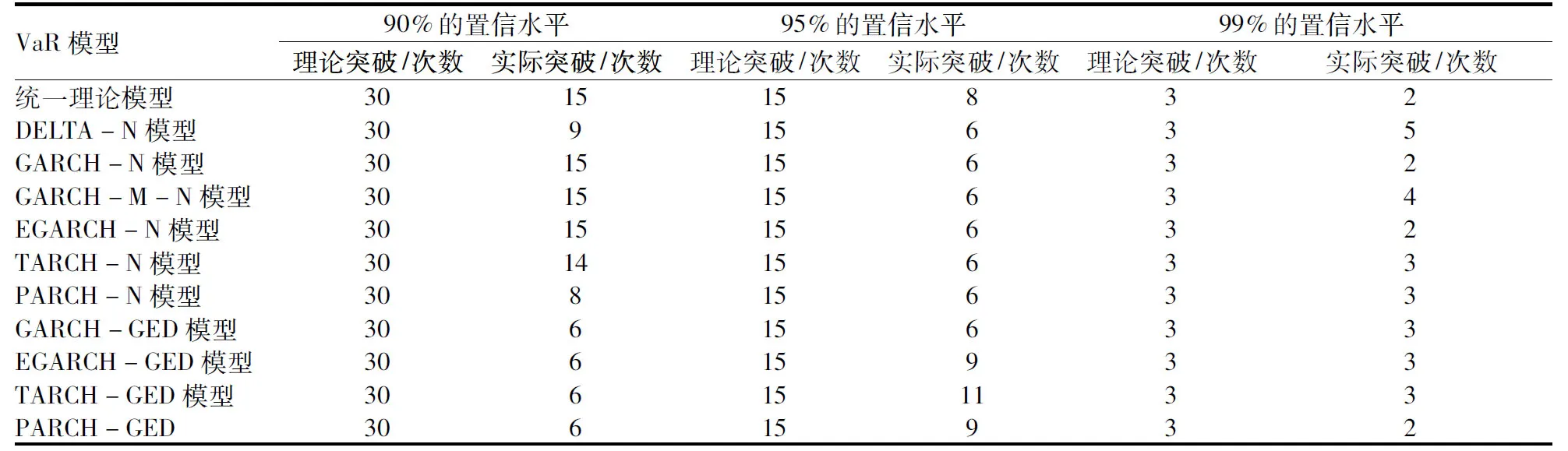
VaR模型90%的置信水平95%的置信水平99%的置信水平理论突破/次数实际突破/次数理论突破/次数实际突破/次数理论突破/次数实际突破/次数理论突破/次数实际突破/次数统一理论模型301515832DELTA-N模型30915635GARCH-N模型301515632GARCH-M-N模型301515634EGARCH-N模型301515632TARCH-N模型301415633PARCH-N模型30815633GARCH-GED模型30615633EGARCH-GED模型30615933TARCH-GED模型306151133PARCH-GED30615932

表3　Kupiec检验结果

注：HS 表示历史模拟法；*、**和***分别表示在 10%、5%和 1%的显著性水平下拒绝原模型。

从表3可以看出，各置信水平下的动态VaR检验结果不一致，在 90%置信水平下，模型都未通过Kupiec检验，说明未考虑时间序列的波动，造成估计的精确度不高。在99%置信水平下，都通过了检验，表明各模型准确性较高，独立性较好。在95%置信水平下，一部分可以通过检验，其中EGARCH-GED和PARCH-GED在 5%的显著性水平下通过检验，HS、EWMA和TARCH-GED在 1%的显著性水平下通过检验，其余的模型都未通过混合Kupiec检验。进一步说明，在 90%置信水平下，EGARCH-N模型的MIXLR 检验值小于另外两者的MIXLR 检验值，表明 EGARCH-N模型突破事件分布相对均匀些，同样 HS、EGARCH-GED 和 PARCH-GED，说明这三个模型突破事件的分布特征不一样。在 95%置信水平下，从MIXLR检验值来看，EGARCH-GED和PARCH-GED模型要优于TARCH-GED模型，原因是EGARCH-GED和PARCH-GED模型突破事件分布比TARCH-GED模型更加均匀。在 99%置信水平下，PARCH-N突破事件的分布没有EWMA 和DELTA-N突破事件分布均匀。接下来将要对各置信水平下动态VaR值进行Kupiec-POF检验，结果显示如表4。

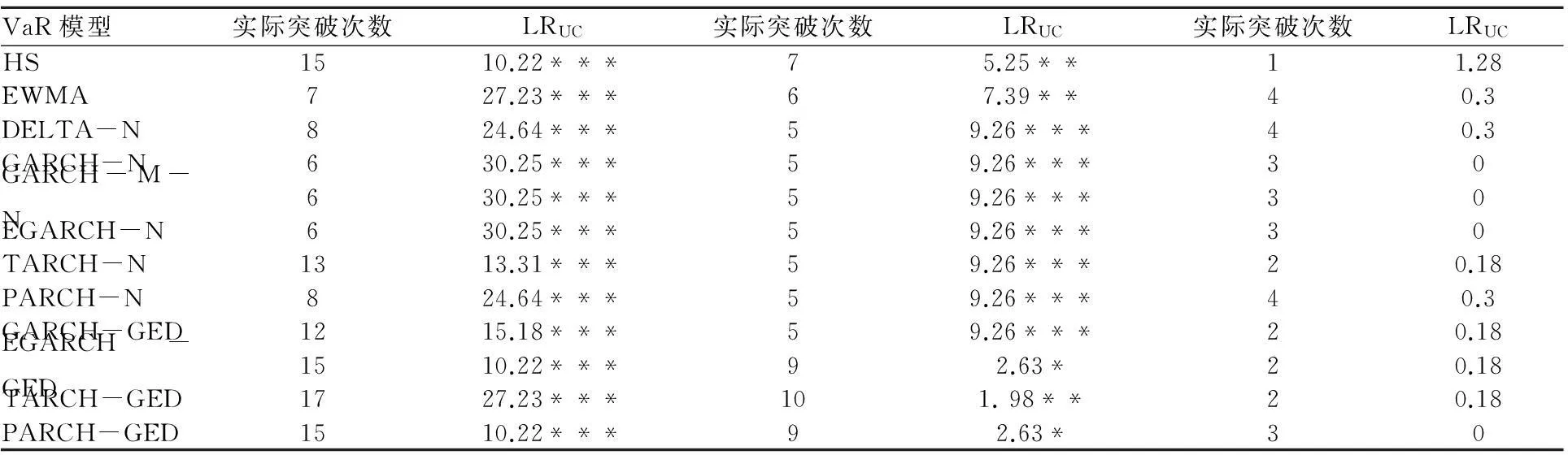
表4　动态VaR值Kupiec-POF 检验结果

注：HS表示历史模拟法；*、**和***分别表示在10%、5%和1%的显著性水平下拒绝原模型。

从表4可以看出，在90%置信水平下， VaR模型都未通过Kupiec-POF检验，说明模型准确性不高， VaR模型都存在高估风险的倾向；在99%置信水平下，VaR模型都通过了检验，表明准确性较高；在 95%置信水平下，一部分VaR模型通过了检验，有些VaR模型估计准确性高，有些模型估计准确性低，观察各模型发现各模型都有高估利率风险的倾向。进一步分析发现：在 95%置信水平下，TARCH-GED在 10%显著性水平下通过Kupiec-POF检验，而仅仅在1%显著性水平通过混合Kupiec检验，由此表明TARCH-GED模型准确性较高，但其混合Kupiec检验结果没有EGARCH-GED和 PARCH-GED检验结果好。另外，EWMA模型没有通过 Kupiec-POF检验，但却在1%显著性水平下通过了混合Kupiec检验，说明 EWMA 模型突破事件分布比较均匀。本文通过混合Kupiec检验的模型进行比较评价，在95%置信水平下通过VaR检验的模型有：HS、EWMA、EGARCH-GED、TARCH-GED和PARCH-GED 五个模型，现选取均值相对偏差和均方根相对偏差两个指标来比较评价这些模型。

表5　日动态VaR值指标统计量

表5统计量结果显示：TARCH-GED模型极其接近平均水平，GED分布下的GARCH族模型的精确性也很高，历史模拟法的估计效果比 EWMA 更为准确。在90%置信水平下，都未能通过混合Kupiec检验；在 99%置信水平下，所有模型都通过了混合Kupiec检验。然后利用指标评价工具对这些模型进行比较评价，利用上述同样的指标来评价。结果显示，在99%置信水平下，正态分布假设下的GARCH族模型精确性较高。

4结论和建议

本文用VaR模型研究了创业板指数的在险价值，实证结果表明：在 99%的置信水平下，各模型估计风险较为准确。在 95%的置信水平下，基于GED分布假设下的GARCH族模型VaR测量风险最精确；在 99%置信水平下，基于正态分布假设下的GARCH族模型VaR测量的准确性较低于基于GED分布假设下 GARCH 族模型。在 95%的置信水平下，其中基于GED分布假设下的非对称的 GARCH族模型准确性高于对称的GARCH模型，说明日收益率波动存在非对称效应。通过分析EGARCH、TARCH和PARCH模型的估计参数发现，日收益率波动存在反杠杆效应，也就是收益率波动的影响对股票市场影响较大。

由此可知，创业板指数中的高新技术企业的股票价格的波动性相对较大，对于创业投资而言，投资过程中面临较高的风险。整体而言，我国创业投资机构波动特征有别于其他金融市场，创业投资的过程中风险较大，具有一定的自相关性；高新技术企业的股票稳定性增长对创业投资的影响更大，股票波动较大对创业投资有巨大风险。

综上所述，创业投资风险管理的力度还要继续加强。第一，政府部门需要完善相关法律法规以适应创投风险管理的客观需要，能够为解决实质性问题提供法律依据。第二，建立健全完善的创业投资基金退出机制，以提高资本的利用效率。第三，创业投资企业谨慎选择和评估投资机会。投资项目之前，深入分析各种影响资本增值和推出的风险，制定相应的风险管理与控制方案，把风险管理纳入到实践中去应用。第四，加强对企业成长的跟踪，企业的成长面临的不确定性会逐渐变大，由于创业企业的管理团队和商务运作模式的缺乏，更多地需要企业的积极介入，加强对企业的跟踪管理，在合适的时机退出，加强对创业企业的监督和风险规避，实现价值的增值。第五，投资后的管理阶段是时间周期最长的阶段，也是创业企业产生代理风险的关键阶段，因此，创投企业在投资后应对自己实施周期性的动态评估，并利用分阶段注资机制来控制被投企业的风险。

参考文献：

[1]Dimitrakopou D N，Kavussanos M G，spyrou S I.Value at risk models for volatile emerging markets equity portfolios [J].The Quarterly Review of Economics and Finance,2010,50 (4) :515-526

[2]Stavroyiannis M V,Nikolaidis L Z.Econometric modeling and Value at Risk using the Pearson type-IV distribution[J].International Review of Financial Analysis.2012 (22):10-17

[3]He K L,Yen J.Value-at-risk estimation of crude oil price using MCA based transient risk modeling approach[J].Energy Economics.2011,33 (5) :903-911.

[4]Hung J C，Chiu C L，Lee M C.Hedging with zero-Value at Risk hedge ratio[J].Applied Financial Economics，2006(03)：259-269.

[5]杨杨,徐文彬.风险价值(VaR)计算方法的实证分析[J].北京信息科技大学学报,2013(04) :83-87.

[6]李汶华,于珊珊,郭均鹏.基于区间分析的投资组合VaR计算新方法[J].数理统计与管理,2013(03) :564-570.

[7]杨夫立.基于GARCH模型的证券投资基金VaR计算与实证研究[J].经济问题,2012 (6): 87-91.

[8]尉轶昊,毛宏.基于VaR约束的最优投资组合选择[J].上海第二工业大学学报,2011(12):298-306.

[9]王春红,曹兴华.VaR法在国债利率风险管理中的应用[J].商业研究,2007(1)：147-149.

VAR MODEL AND ITS APPLICATION IN THE VENTURE

INVESTMENT RISK MANAGEMENT

——Empirical research based on the gem index

YE Jin1,GU xiu-juan2

(1.ZhengzhouXinyiRoadBranch,MinshengBank,Zhengzhou450004,China;

2.SchoolofEconomics&Trade，HenanUniversityofTechnology,Zhengzhou450001,China)

Abstract:There are many serious risks involving the operation of venture capital,hence,the need to measure and evaluate the risk of venture capital.In this paper,the VaR model is established,and the daily return rate and the stock closing price of the gem index from January 1,2014 to December 31,2014 are used as samples to conduct measurement and empirical study of the risk of venture capital.The empirical results show that the stock price fluctuation of China′s high-tech enterprises and small and medium-sized enterprises is bigger,and the risk is higher,therefore, the risk confronted by venture capital institutions is relatively high,and venture capital institutions have to conduct a repeated and phased assessment of investment object，take a portfolio investment in the process of investment and strengthen the supervision and management of investment to spread and control risk.

Key Words：venture capital;VaR model;risk management

中图分类号：F830.593 X820.4

文献标识码：A

文章编号：1673-1751(2015)04-0082-06

作者简介：叶金(1990-)，男，河南周口人，硕士研究生,研究方向：金融工程与风险管理

基金项目：2013年国家社会科学基金资助项目(13BJY085)。

收稿日期：2015-08-25