一种解决柔性车间作业调度问题的粒子群优化算法*

刘　韵，胡　毅，罗　企，房　超

(1.中国科学院大学，北京　100049；2.中国科学院 沈阳计算技术研究所 高档数控国家工程研究中心，沈阳　110168；3.沈阳高精数控技术有限公司，沈阳　110168)



一种解决柔性车间作业调度问题的粒子群优化算法*

刘韵1，2，胡毅2，3，罗企1，2，房超1,2

(1.中国科学院大学，北京100049；2.中国科学院 沈阳计算技术研究所 高档数控国家工程研究中心，沈阳110168；3.沈阳高精数控技术有限公司，沈阳110168)

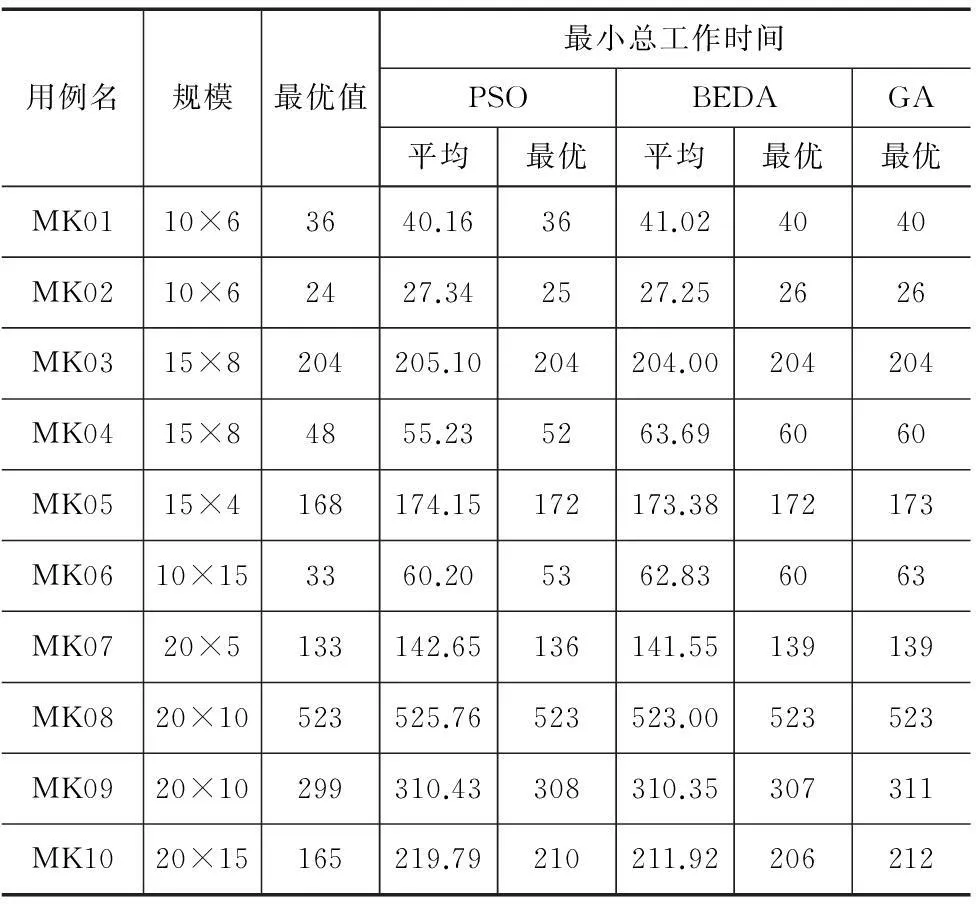
摘要：柔性车间作业调度问题(FJSP)作为经典车间作业调度问题(JSP)的扩展，早在上个世纪已经被证明为是NP-难的问题。目前启发式搜索方法作为解决NP-难问题的一个重要方法，已经被广泛用于解决车间调度问题。文章提出了一种基于启发式搜索的粒子群优化算法(PSO)，用以解决柔性车间作业调度问题，旨在获得最优的最小总工作时间。实验的结果与基于分布式估计算法(BEDA)以及改进后的遗传算法(GA)比较，证明本文提出的PSO算法，可以有效处理FJSP问题。

关键词：车间作业调度；启发式；粒子群；NP-难

0引言

在现实车间生产中，作业调度的好坏直接影响着生产效率。车间作业调度问题作为组合优化问题的一个典型代表加上它与生俱来的特点，导致其必然很难解决，事实上其也被证明为是NP-难问题。过去五十多年的研究中，科学家们尝试了各种方法[1]，最早的是一些确定性算法，典型的如分支界定算法，不过随着作业和机器数量的增加，问题的复杂性呈指数增长，这些算法无法满足解决问题的需求。鉴于此，大多数科学家开始尝试使用非确定性算法，比如遗传算法[2-3]等。然而由于车间作业调度问题属于NP-难问题，不论是确定性算法，还是非确定性算法，至今都没有一个算法能在确定时间内找到最优解。因而近些年来，学者们都将目光转向先找到局部最优解，再经过有限次的循环，尽可能趋向最优解。

1柔性车间作业调度研究情况

过去的二十多年中，基于领域搜索的一些算法一度成为车间作业调度问题研究的主角，比如禁忌搜索的算法，Faccio[4]提出的模拟退火等算法来解决问题。不过由于基于领域的搜索算法太过依靠初始值或种群，很容易导致提前收敛，而远离最优解。因而，学者们今年来更多的转向一些种群优化策略，比如蜂群优化[5]、蚁群优化[6]、人工免疫[7]以及本文涉及的粒子群优化[8-9]等方法。目前更多的学者尝试结合两种以上的算法来弥补各独立算法的不足，比如Liouane[10]等人提供了一种结合蚁群优化和禁忌搜索的方法，来获得最小的总工作时间；Rossi和Dini[6]则结合遗传算法和蚁群优化方法，在更宽松的作业限制条件下获得最优解决方案。

作为启发式搜索算法的一种，粒子群优化算法已经应用到解决车间作业调度的问题上来了，而且表现出不错的效果。本文后续内容将首先具体描述柔性车间作业调度问题并公式化各种规范及限制条件，再详细地描述一种粒子群算法，并应用到柔性车间作业调度问题上，最后再将此算法的结果与两种算法进行比较并提出一些展望。

2柔性车间作业调度问题描述

柔性车间作业调度问题是指n个作业，每个作业包含一定数量的工序，而且工序间有固定的前后关系，并且将工序在m台机器上处理的问题。对于作业，工序，机器，它们之间有一定的限制条件，可以用文字描述如下：

①各个作业间是相互独立的，不存在先后关系；

②每个机器在任一时间只能处理一个作业；

③各作业一旦进行操作，就不能中断或取消；

④所有作业的初始时间都相同，假设都是0；

⑤当作业在一台机器上处理完一个工序，转向另外一个机器的转换时间忽略不计；

⑥一个工序可能可以在多台机器上处理；

⑦目标是获取最下的总工作时间；

问题的数学表达可表述如下：

(1)

Si,j+1-Cij>0,∀i,j

(2)

表示一个工序只有在之前的工序处理完成后才能开始处理。

Ci′j′-Cij+H(1-Yiji′j′)+H(1-Xijk)+

H(1-Xi′j′k)≥tijk,∀Oij,Oi′j′∈Nk

(3)

表示每个机器在某一时间某个机器只能处理一个工序。

(4)

一个工序的处理时间是结束时间和开始时间的差值。

目标是Minimize[Max(C1,J1,C2,J2,...,Cn,Jn)]

(5)

Ji、Mi表示第i个作业或机器，Oij表示第i个作业的第j个工序。

Sij表示Oij的开始时间，Cij表示Oij的完成时间，tijk表示Oij在Mk上的处理时间。

H表示一个很大的正整数，Nk表示能在Mk能处理的所有工序。

3粒子群解决柔性车间作业调度问题

算法的各个流程显示如图1所示。

(1) 数据输入：输入的数据如下：

①待处理的作业集合Jn。

② 可选用的机器集合Mn。

③ 每个作业的工序集合Oij。

④ 每个工序可以选择的路径Rij。

⑤每个工序Oij的每个路径对应的机器Mk以及在此机器上处理该工序的时间tijk。

如表1 所示，是一个输入实例，该实例是由三个作业组成，每个工序有三个工序，每个工序有两个路径，即两个可选择的机器。

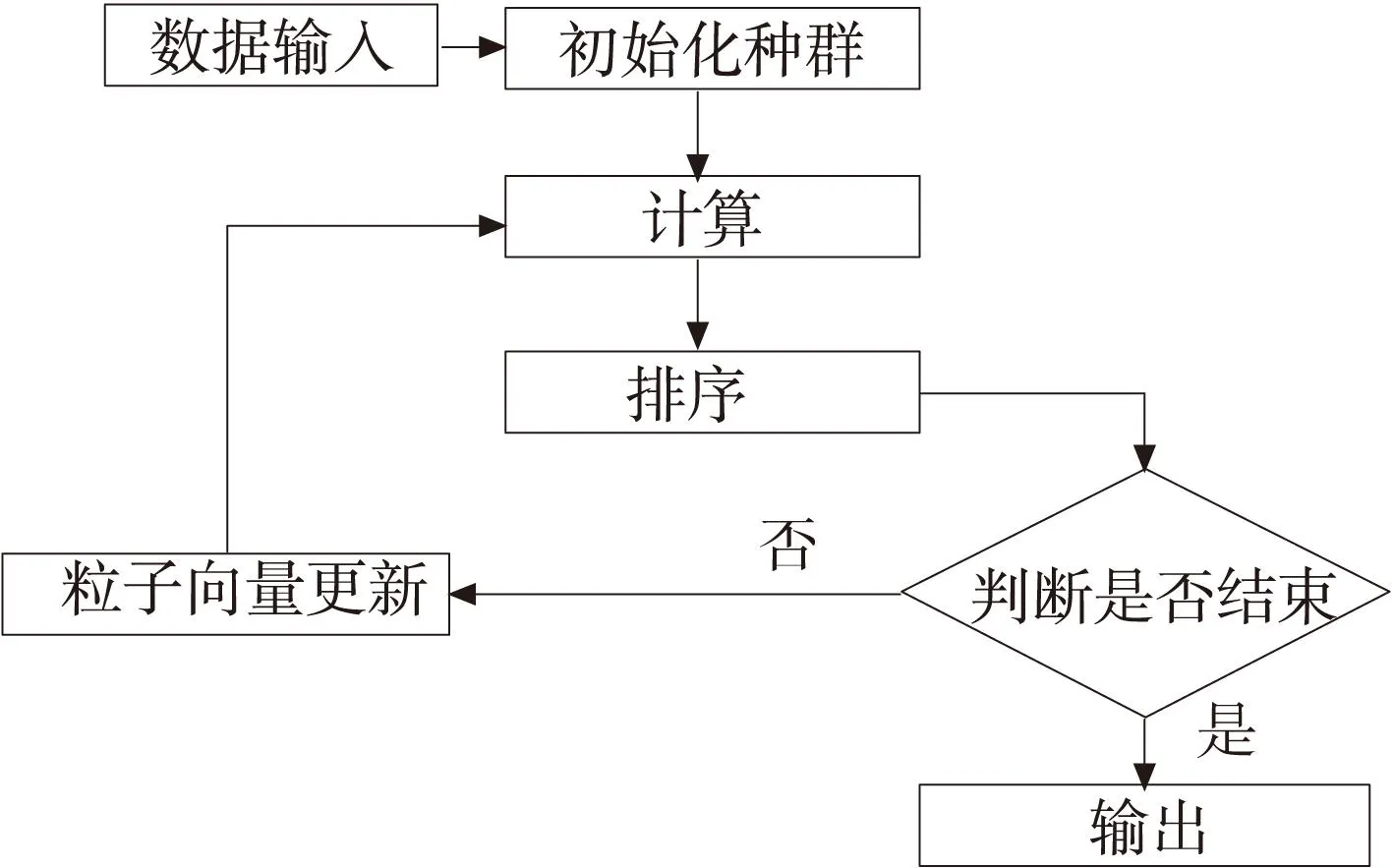
图1　算法流程

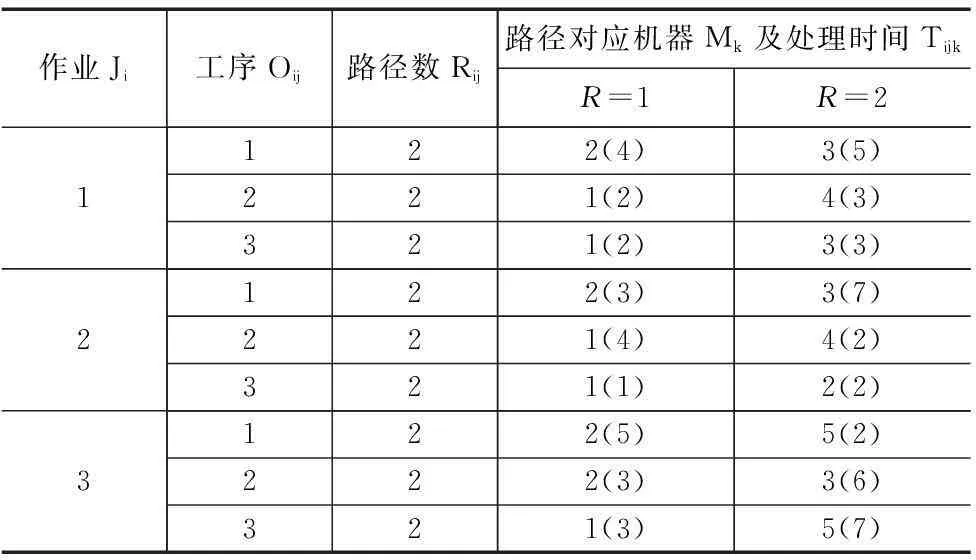
作业Ji工序Oij路径数Rij路径对应机器Mk及处理时间TijkR=1R=21122(4)3(5)221(2)4(3)321(2)3(3)2122(3)3(7)221(4)4(2)321(1)2(2)3122(5)5(2)222(3)3(6)321(3)5(7)

(2)初始化种群：设定粒子总数表示为particle_swarm_size，并在这个部分对每个粒子进行随机初始化。每个粒子q由一个位置向量particle_pos(q)组成，q为粒子编号。Particle_pos(q)向量由两部分组成，第一部分是每个工序在本次处理选择的路径的集合，第二部分表示这些工序对应的优先级的集合，数字越大优先级越高。每个工序分配不同的优先级，这个优先级在第三部分计算粒子的可行解时，作为在在同一机器上处理的工序的顺序的依据。表2所示为粒子初始值的一个实例。粒子的每个工序的路径选择和优先级在初始的时候都是随机产生的。

表2　一个粒子随机产生的数据

(3)计算：计算是通过确定位置向量particle_pos(q)中第一部分的路径，即选定每个工序的处理机器，将其转换为经典车间作业调度问题来处理的。然后通过第二部分的优先值，再将问题再将其转换成一个固定的作业调度问题，解决冲突。本文使用构建甘特图的方式来求得当前粒子的一个可行解，如图2所示，通过构建甘特图可以得出该粒子的一个可行解，以及最小总工作时间为16，本文用particle_sol(n)表示，即为particle_sol(n)=16，其中n为循环的次数。

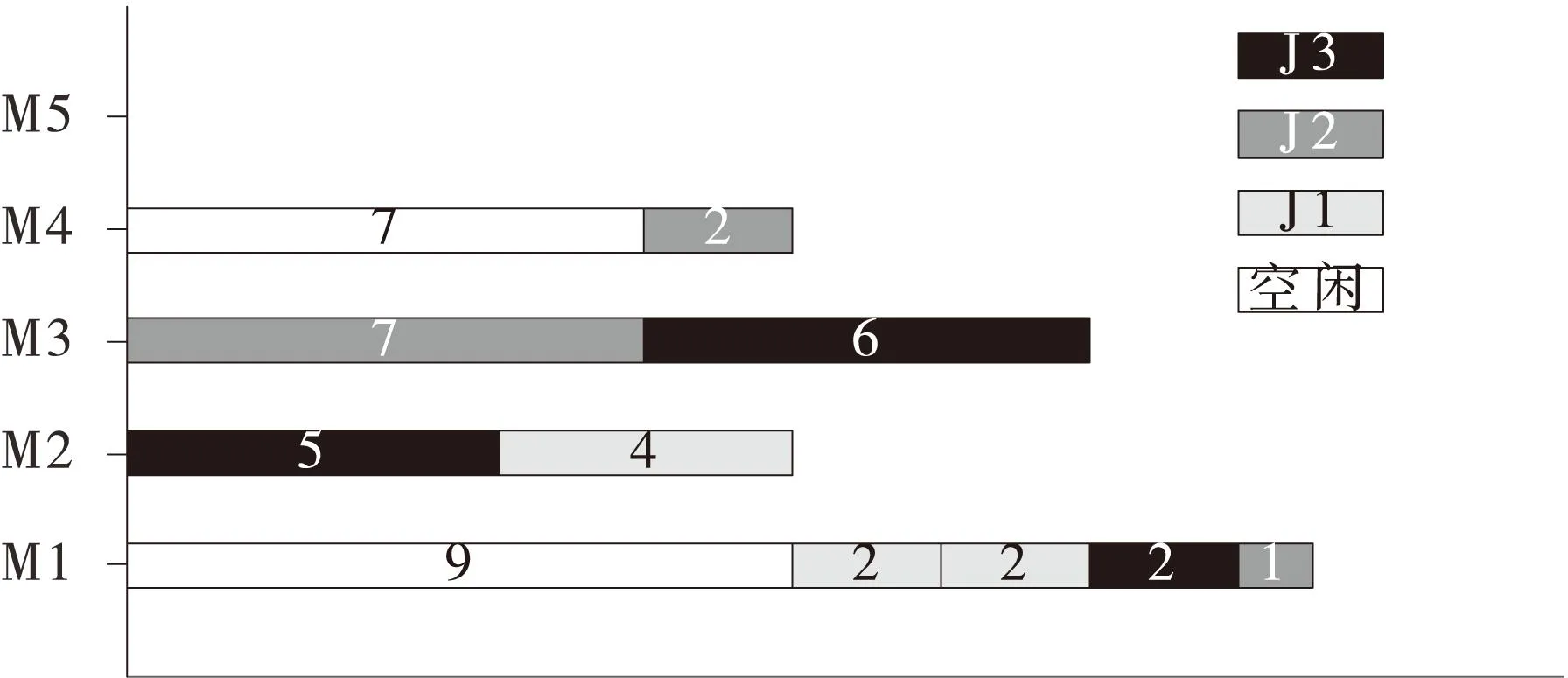
图2　实例粒子的甘特图结果

(4)排序：在每轮循环中，遍历每个粒子的解particle_sol(q)与当前的最优解相比较(使用particle_best_sol(n)表示，n为循环的次数)。如果particle_sol(q)

表3　一个粒子群输入实例

如表3所示，是一个particle_swarm_size=10的初始粒子群实例。从计算结果中可以得出当前particle_best_sol(1) = 14，而且由于是初始种群，全局最优解global_best=particle_best_sol(1)。

(5)判断是否结束：设定在循环generation_num次数后结束，一般选择设定generation_num=count(Job)* 100，即作业总数的100倍。对于上述的实例，我们选择generation_num为300。

(6) 粒子向量更新：此部分中每对个粒子以上轮循环的结果particle_best_pos(n-1)和当前全局最优解global_best_pos为参照目标进行更新。更新的速度和每个粒子新的位置向量决定于以下因素：

D1=particle_best_pos(q) 和 particle_pos(q)中不一样的元素，即路径r和优先值p不相同的工序。

D2=global_best_pos 和 particle_pos(q)中的不一样的元素，与D1含义相同。

其中 particle_pos(q) 移向 particle_best_pos(q)的速度表示为V1=c1，particle_pos(q)移向global_best_pos的速度表示为V2=c2，其中c1,c2∈(0,1)，其值由初始时设定。

本文是通过一种插入和交换机制来推动particle_pos(q)向上一轮的particle_best_pos(n-1)以及当前全局最优解global_best_pos靠拢的。插入操作主要用与particle_pos(q)的路径选择部分，而交换操作主要用于particle_pos(q)的优先级部分以防止出现相同的优先值。

首先，分别比较particle_pos(q)和particle_best_pos(n-1)每个元素的路径选择和优先值部分。并根据比较结果，并且将所有需要改变的元素,即不同的元素，保存在D1中。同样对particle_pos(q)和global_best_pos进行上述操作，并保存在D2中。此时D1和D2就分别保存了particle_pos(q)向particle_best_pos(n-1)和global_best_pos靠拢所需进行的插入和交换操作。

然后，对于每个插入或交换操作，在(0,1)中去一个随机数rand()，如果rand()

但是仅仅使用插入交换机制，会面临大部分启发式搜索算法都会遇到的共同问题，就是过早的收敛。为了避免所提出的粒子群优化算法过早收敛，本文使用了一种变异机制，通过一定的概率p_mut来进行变异操作。即particle_pos(q)中的元素会以概率p_mut随机产生新的元素。

如表4示例，取V1=0.6 ，V2=0.4，p_mut=0.05。表中描述的是一个粒子，与particle_best_pos(n-1)以及global_best靠拢的过程。靠拢过后产生的结果作为下一轮循环的输入部分。

(7) 输出：当算法达到结束条件时，这个部分将输出全局最优解global_best_pos，以及最小总工作时间，并根据计算结果显示甘特固。

4实验结果

本文提出的PSO算法，是在Ubuntu14.04-64bit操作系统，Intel Core i5-3210M处理器，8GB运行内存的硬件环境上测试的结果。使用编程语言是C语言。测试用例选用的是MK系列的标准测试用例。

对于本次实验，我们选用的PSO的初始参数为particle_swarm_size=count(Job) * 10，c1=0.4，c2=0.6以及p_mut=0.05的初始值。结束条件是达到循环一定的循环次数，在这里我们选择循环次数i为作业数量的100倍。实验结果是运行10次的平均结果。

本文提出的PSO算法与Ling Wang[11]等提出的基于分布式估计算法(BEDA)以及F. Pezzella[12]等提出的改进的遗传算法(GA)进行比较。

表5　与BEDA和GA比较

从实验结果对比看，对于MK01-MK05等5个测试用例PSO算法得到的值要明显高于BEDA和GA，对于数量规模相对较大的MK06-Mk10等5个测试用例，PSO算法的结果要好于GA，而与BEDA相似。对于MK03和MK08两个测试用例，三个算法都显示出相对比较稳定的计算结果，平均值都能非常接近于最优值。而对于MK10，三个算法的偏离的都相对较多，可能的是陷入局部过早收敛导致。为了提高算法的效果，我们将在以后对算法的各个参数进行完善。

5结论与展望

本文中提出了一种基于启发式搜索的粒子群优化算法来解决柔性车间作业调度问题，以获取最小总工作时间。用位置向量的形式表示，使得算法可以有效地搜索所有可能的结果，因而可以找到最优解或者是近似的最优解。在应用到一系列标准测试用例后，可以发现与现有的算法相比，PSO算法具有相当的竞争力。

下一步，我们将尝试将粒子群优化算法与一些局部搜索算法如模拟退火算法、禁忌搜素算法等相结合，或许会有更优的表现。目前V1和V2等参数还是固定值，之后也考虑使用可变化的值，观察是否有更好的结果。

[参考文献]

[1] 李传鹏, 王桂从, 崔焕勇. 柔性作业车问调度问题研究现状及发展趋势[J]. 组合机床与自动化加工技术, 2013 (11): 109-112.

[2] 陆曈曈, 胡方军, 张屹. 一种求解作业车间调度问题的异步元胞遗传算法[J]. 组合机床与自动化加工技术, 2014 (8): 147-151.

[3] 齐晓宁, 汪永超, 贾婧, 等. 基于遗传算法的面向绿色制造的车间调度优化[J]. 组合机床与自动化加工技术, 2012 (10): 16-18.

[4] Faccio M, Ries J, Saggiorno N. Simulated annealing approach to solve dual resource constrained job shop scheduling problems: layout impact analysis on solution quality[J]. International Journal of Mathematics in Operational Research, 2015: 1-21.

[5] Li J Q, Pan Q K, Tasgetiren M F. A discrete artificial bee colony algorithm for the multi-objective flexible job-shop scheduling problem with maintenance activities[J]. Applied Mathematical Modelling, 2014, 38(3): 1111-1132.

[6] Rossi A, Dini G. Flexible job-shop scheduling with routing flexibility and separable setup times using ant colony optimisation method[J]. Robotics and Computer-Integrated Manufacturing, 2007, 23(5): 503-516.

[7] Lau H Y K, Qiu X. An Artificial Immune Systems (AIS)-based Unified Framework for General Job Shop Scheduling[J]. 2014.

[8] Girish B S, Jawahar N. A particle swarm optimization algorithm for flexible job shop scheduling problem[C]//Automation Science and Engineering, 2009. CASE 2009. IEEE International Conference on. IEEE, 2009: 298-303.

[9] Tavakkoli-Moghaddam R, Azarkish M, Sadeghnejad-Barkousaraie A. A new hybrid multi-objective Pareto archive PSO algorithm for a bi-objective job shop scheduling problem[J]. Expert Systems with Applications, 2011, 38(9): 10812-10821.

[10] Liouane N, Saad I, Hammadi S, et al. Ant systems & local search optimization for flexible job shop scheduling production[J]. International Journal of Computers, Communications & Control, 2007, 2(2): 174-184.

[11] Wang L, Wang S, Xu Y, et al. A bi-population based estimation of distribution algorithm for the flexible job-shop scheduling problem[J]. Computers & Industrial Engineering, 2012, 62(4): 917-926.

[12] Pezzella F, Morganti G, Ciaschetti G. A genetic algorithm for the flexible job-shop scheduling problem[J]. Computers & Operations Research, 2008, 35(10): 3202-3212.

(编辑赵蓉)

Solving Flexible Job-shop Scheduling Problem with a Particle Swarm Optimization Algorithm

LIU Yun1,2，HU Yi2,3，LUO Qi1,2，FANG Chao1,2

(1. University of Chinese Academy of Sciences, Beijing 100049，China；2. National Engineering Research Center For High-End CNC, Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168,China)

Abstract：Flexible Job Shop Scheduling Problem (JSP), which as an extension of Classical Job Shop Scheduling Problem, had been proved as NP-Hard problem since last century.As one of the most popular approaches, heuristic search has been widely used for solving Job Shop Scheduling Problem. In this paper, we propose an Particle Swarm Optimization(PSO) Algorithm, which based on heuristic search, to solve the Flexible Job Shop Scheduling Problem. Compared with Based Estimation of Distribution Algorithm and Improved Genetic Algorithm proves that the algorithm we proposed can solve the FJSP effectively.

Key words：job shop scheduling；heuristic； particle swarm；NP-Hard

中图分类号：TH165；TG506

文献标识码：A

作者简介：刘韵(1990—)，男，安徽定远人，中国科学院大学、中科院沈阳计算技术研究所硕士研究生，研究方向为网络化的数控系统，(E-mail)ahlyun@126.com。

*基金项目：“高档数控机床与基础制造装备”国家科技重大专项、基于二次开发平台的专用数控系统开发与应用(2013ZX04007-011)

收稿日期：2015-02-09；修回日期：2015-03-01

文章编号：1001-2265(2015)12-0144-04

DOI:10.13462/j.cnki.mmtamt.2015.12.039