基于模糊综合评价法的数控机床可靠性评估修正系数计算*

夏仰球，舒　强，胡　秋

(中国工程物理研究院 a.机械制造工艺研究所；b.机床装备检测评价中心，四川 绵阳　621900)



基于模糊综合评价法的数控机床可靠性评估修正系数计算*

夏仰球a,b，舒强a,b，胡秋a

(中国工程物理研究院 a.机械制造工艺研究所；b.机床装备检测评价中心，四川 绵阳621900)

摘要：针对数控机床可靠性试验评价中的修正系数影响因素多、影响效果存在模糊性的特点，提出了基于模糊综合评价法的可靠性修正系数计算方法。通过分析影响可靠性修正系数的关键因素，建立由试验数据归一化的影响因素集；应用三角隶属函数构建一级模糊综合评判矩阵，结合专家评分系统形成最终的综合评判矩阵；利用适用于个体识别的最大隶属度原则进行评判，获得可靠性修正系数。采用试验场试验方式对国产某加工中心进行了可靠性评估试验，其MTBF值与同型号5台机床连续4年现场跟踪统计试验MTBF值吻合较好，表明模糊综合评价法能够较好解决数控机床可靠性评估修正系数计算问题。

关键词：数控机床；可靠性评估；修正系数；模糊综合评价；评分机制

0引言

数控机床可靠性试验与评估是获取装备故障信息、进行可靠性分析与评价、实施可靠性增长等可靠性研究的重要基础。

国产数控机床与欧洲等先进国家数控机床在可靠性方面存在较大差距[1]，为此我国在《高档数控机床与基础制造装备》科技重大专项实施过程中，对数控机床整机及关键功能部件(滚动功能部件、主轴、刀库等)开展了可靠性设计、制造、试验与评估、可靠性增长等全方位研究以期尽快提高国产数控机床可靠性，并把可靠性评估明确为产品研制项目关键验收指标。

数控机床是复杂机电装备典型代表之一，由于其系统的复杂性、载荷的随机性、工况的非线性、样本的稀有性和昂贵性，对数控机床进行准确、有效的可靠性评估成为业界的难点之一。

平均故障间隔时间(MTBF)是评价数控机床可靠性的重要指标[2]。国家标准GB/T 23567.1《数控机床可靠性评定 第1部分：总则》[3]规定，数控机床可靠性测定可采用试验场试验和现场跟踪统计试验两种方式，但对新研制产品必须采用试验场试验。同时现场统计跟踪试验每台样机累积相关试验时间应大于2000小时，试验时间太长。因此试验场试验是一种重要的评估方式。

对于试验场试验可靠性评估试验，呈指数分布的数控机床MTBF点估计为：

(1)

式中，m—MTBF的点估计值；Tj—评定周期内第j机床累积工作时间；rj—评定周期内第j台机床累积故障数；k—可靠性修正系数。

标准规定：

k=kAkTkS

(2)

式中，kA—加速系数(与强化条件有关)；kT—工况系数(与转速、工作期限、功率、环境等有关)；kS—寿命系数(与材料、受载等有关)。

但是标准没有说明各系数的具体计算方法，操作性不强。在可靠性试验评价研究方面，北京工业大学黄祖广[4]通过研究加工中心加速可靠性试验载荷谱、故障模式及故障机理等可靠性试验关键技术，建立了基于实验室的加工中心加速可靠性试验平台和小子样产品可靠性评价技术。吉林大学陈炳锟[5]研究了基于威布尔分布的数控机床定时截尾试验和定数截尾试验，并结合传统序贯试验方案的设计方法，设计了数控机床的序贯试验方案，利用数控机床故障率的先验信息，将贝叶斯理论引入到可靠性试验研究中，建立了基于贝叶斯理论的定时截尾试验方案。重庆大学李世龙[6]考虑到数控机床的复杂性与数据的不确定性，研究了基于改进的模糊层次分析法的数控机床可靠性分配方法，系统的分析了数控机床的故障数据，制定了基于寿命周期的数控机床可靠性增长及管理办法。

可靠性修正系数影响因素众多，它与强化条件、转速、工作期限、功率、环境、材料、受载等诸多因素有关，且各因素对修正系数的影响程度不定，存在模糊性。许多学者[7-12]将模糊算法应用于可靠性评估。文献[7-10]将专家打分、层次分析法与模糊数学有机结合，研究了可靠性分配优化方法。文献[11-12]分析了MTBF、MTTF等在可靠性评估中的权重，从而利用模糊综合评价法对设备可靠性进行评估。未见关于可靠性修正系数计算的相关报道。本文提出一种基于模糊综合评价法的可靠性修正系数计算方法。

1修正系数模糊综合评价法

1.1修正系数影响因素分析

从前述可靠性指标MTBF点估计计算公式中可以看出，描述可靠性模拟质量的可靠性修正系数k成为评价结果准确性的关键。

试验场试验为缩短试验时间，采用强化试验的方法进行可靠性试验[3,13]。试验方法是对故障多发部位(进给轴、主轴、刀库等)进行强化试验，并对整机进行综合考核，其主要强化方法包括增大加载力、增加换刀次数、提高主轴转速和进给速度等方式，同时延长重载时间比例。

试验提取加载力、加载时间及实验时间、换刀频繁度、转速利用率、功率以及温升等试验参数，与机床的正常工作状态比较分析，计算可靠性修正系数。

1.2快速可靠性试验数据处理

为方便计算分析，将加载力、加载时间、换刀频繁度、转速、功率以及温升等试验数据进行归一化处理。

1.2.1加载力系数k1

可靠性加载试验在模拟机床实际工作载荷的基础上增强了加载力度，其系数用平均加载力与机床最大切削抗力的比值表示：

(3)

式中，n—加载次数；Fi—单次加载力，单位N；Fmax—机床最大切削抗力，单位N。

1.2.2加载时间系数k2

可靠性试验加载时间体现了加载力的时间累积效应，提高了载荷破坏几率，其系数用加载总时间与试验总时间的比值表示：

(4)

式中，n—加载次数；ti—单次加载时间，单位s；t—试验总时间，单位s。

1.2.3换刀频繁度系数k3

加大换刀频繁度也是提高机床载荷的一种表现形式，其系数用试验平均换刀频繁度与参考换刀频繁度的比值表示：

(5)

式中，N—试验换刀总次数；T—试验总时间，单位h；M—试验参考换刀频繁度，单位h-1。

1.2.4转速利用系数k4和功率利用系数k5

转速和功率大小表征了机床主轴运转强度，都是影响机床寿命的重要参数，转速利用系数用平均试验转速与机床最高转速的比值表示：

(6)

式中，ni—转速，单位r/min；ti—ni转速下运行时间，单位s；T—试验总时间，单位s；nmax—机床最高转速，单位r/min。

功率利用系数用平均试验功率与机床额定功率的比值表示：

(7)

式中，Pi—功率，单位kW；ti—Pi功率下运行时间，单位s；T—试验总时间，单位s；P—额定功率，单位kW。

1.2.5温升影响系数k6

温升大小体现了机床运行状态，温升的高低直接影响着机床性能，试验采用标准规定的温升测定方式进行多次检测，其系数用平均温升余量与允许最高温升的比值表示：

(8)

式中，n—试验次数；Ti—单次温升，单位℃；Tmax—允许最高温升，单位℃。

1.3快速可靠性修正系数计算方法

考虑影响快速可靠性评估修正系数的因素，建立因素集

(9)

这些因素的高低、优劣选用“很低、低、中、高、很高”五级表示，则因素等级集

(10)

由于各个因素的模糊性以及其等级的模糊性，各个因素应视为等级集上的模糊子集，即

(11)

参照GB/T 9061-2006《金属切削机床 通用技术条件》、JB/T 8801-1998《加工中心 技术条件》规定和以往可靠性评价分析经验，各指标的评价标准界限值如表1所示。

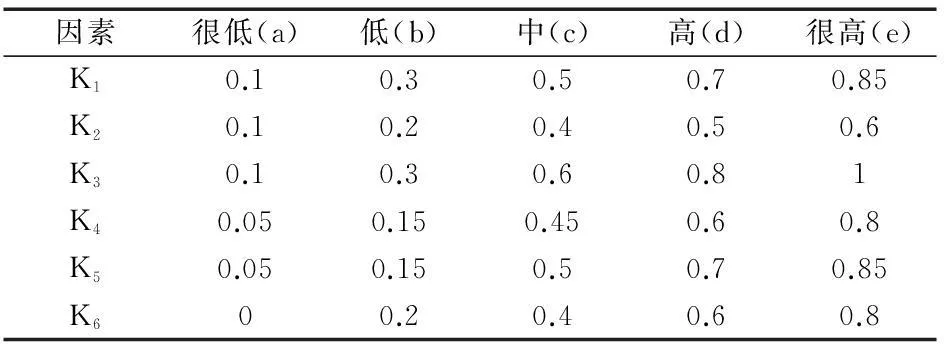
表1　评价界限值

在机械产品性能评价时，常采用折线型隶属函数[14]，因此，根据加工中心可靠性指标特性和等级模糊集合，采用三角型隶属函数，式(12)～式(16)，其函数示意图如图1所示。

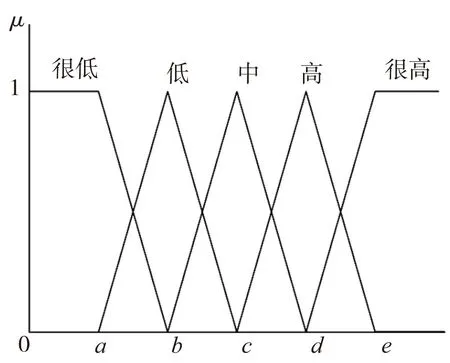
图1　三角隶属函数示意图

(12)

(13)

(14)

(15)

(16)

依据可靠性修正系数k的取值区间取值特征,建立备择集V。

各因素等级评判集

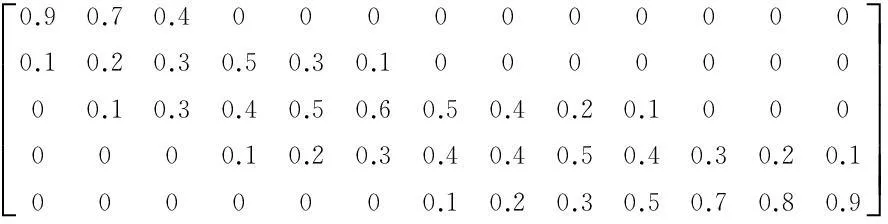
一级模糊综合评判矩阵

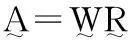
(17)

专家打分确定各因素的权重Wu，每项因素影响系统工作寿命的最高分数为1，分数为1表明该项影响因素的大小严重影响系统的工作寿命。第j位专家对第i项因素打分为pij，则第i项的总分为

(18)

权重

(19)

(20)

二级模糊综合评判矩阵

(21)

针对个体识别应用最大隶属度法评判[15]

(22)

选评判指标中最大的Bp(1≤p≤k)对应的备择集中的Vp值。

2应用实例

试验对象为某国产数控立式加工中心，该型号机床共5台，其基本参数见表2。

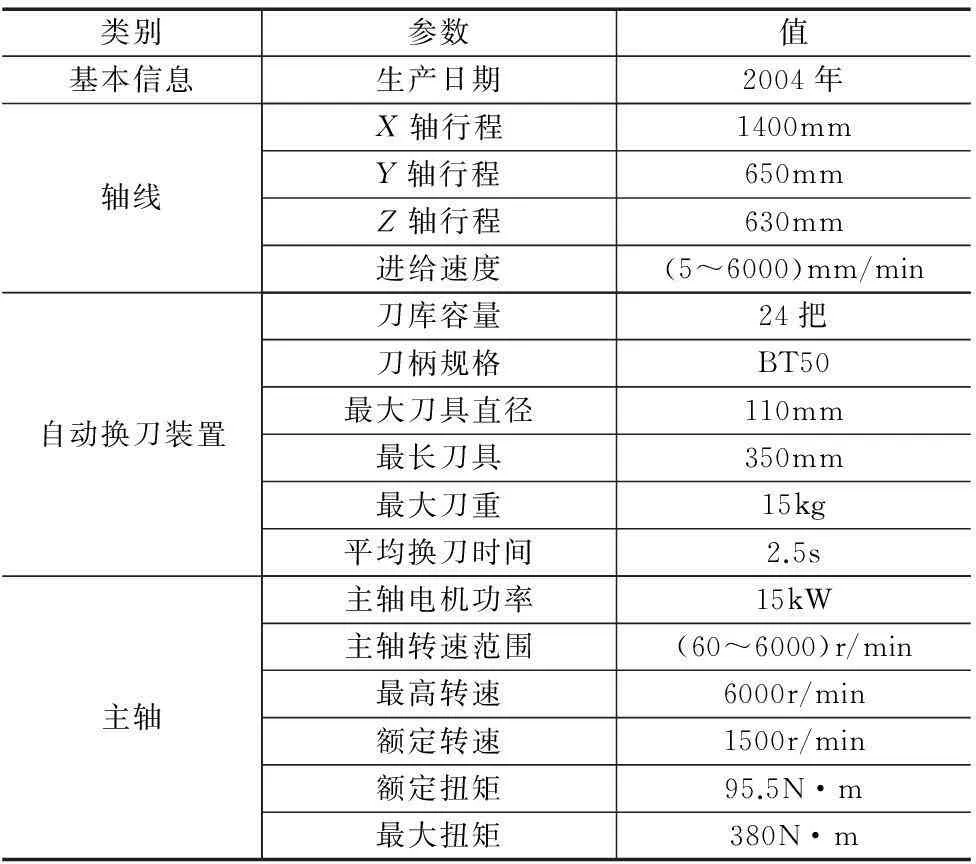
表2　数控立式加工中心基本参数

试验采用试验场试验，无替换定时截尾试验，试验时间220小时，试验加载方式如图2所示，单次加载循环试验参数见表3。

图2　加载试验

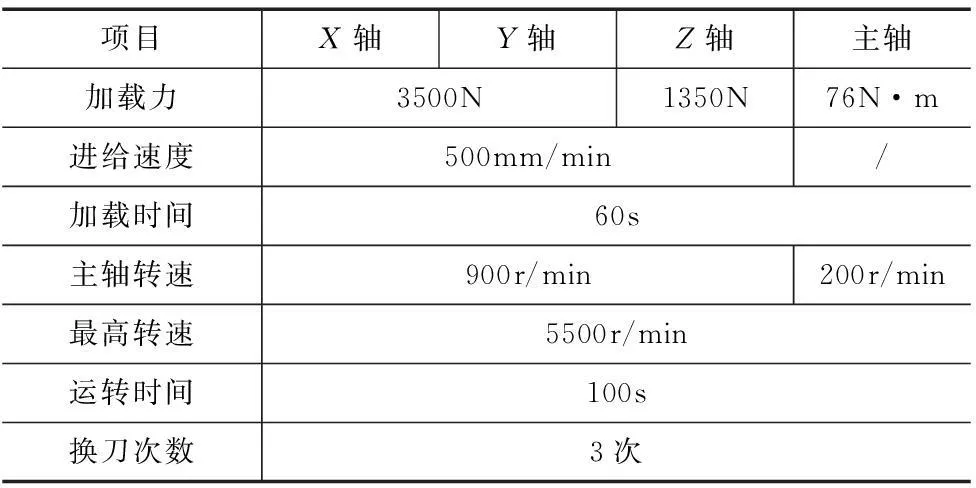
项目X轴Y轴Z轴主轴加载力3500N1350N76N·m进给速度500mm/min/加载时间60s主轴转速900r/min200r/min最高转速5500r/min运转时间100s换刀次数3次

试验数据按第2节方法处理，结果见表4。

表4　试验结果

根据测试结果，代入隶属函数得等级权重集，得：

快速可靠性评估修正系数K的取值区间在〔1,6〕,按等步长原则在该区间内取一系列离散点,得备择集。

V=

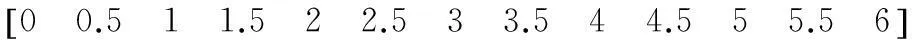
计算二级模糊综合评判矩阵：

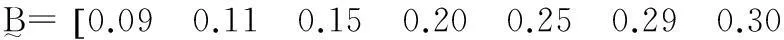
表5　专家打分统计表

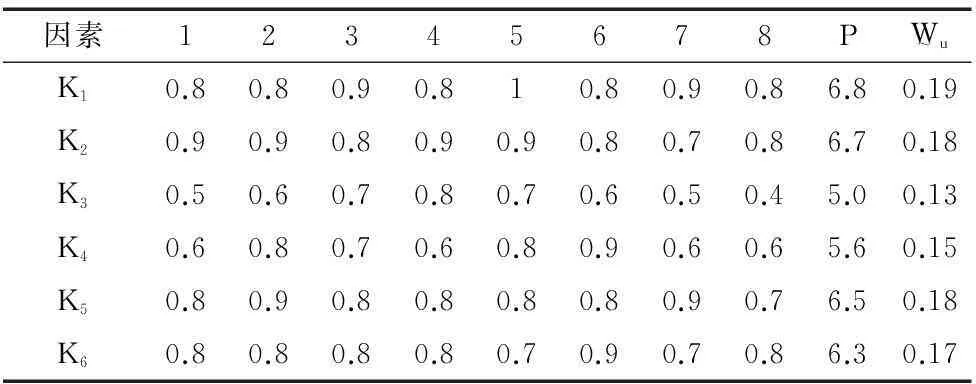
因素12345678PW～uK10.80.80.90.810.80.90.86.80.19K20.90.90.80.90.90.80.70.86.70.18K30.50.60.70.80.70.60.50.45.00.13K40.60.80.70.60.80.90.60.65.60.15K50.80.90.80.80.80.80.90.76.50.18K60.80.80.80.80.70.90.70.86.30.17

试验共进行了时间220小时，期间发生3次故障，分别为主轴高速异响、机械手松刀故障以及刀库选刀故障。按最大隶属度法评判得k=3，MTBF=220小时。

利用单位产品制造信息系统和设备故障维修系统，分析了5台同年月购置并投入使用的同型号机床四年(2011年1月1日至2014年12月31日)的故障数据，得表6统计数据及表7故障统计表。从图表中可以看出统计MTBF为231小时，故障集中在主轴系统、刀库及机械手、进给轴系统、电气及数控系统等部位，与试验结果相近。

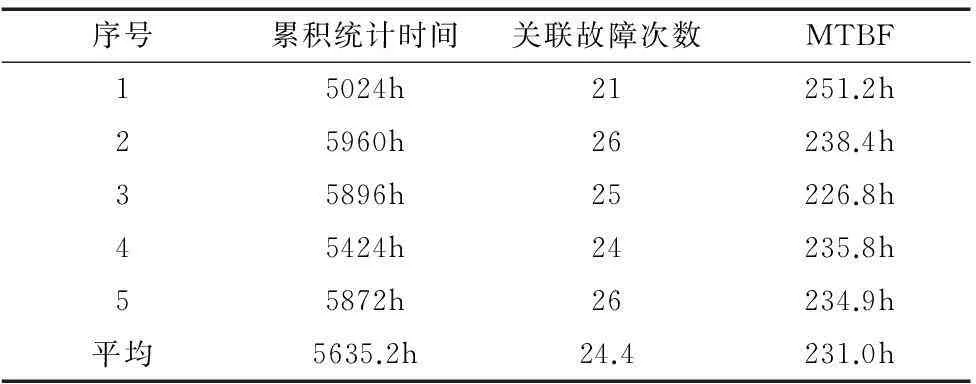
表6　统计数据

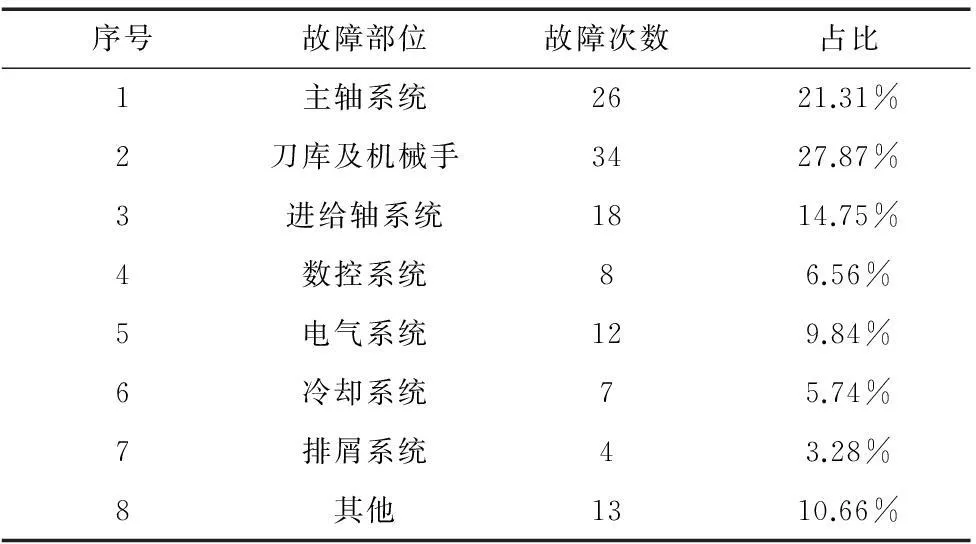
表7　故障统计表

3结论

(1)结合试验场试验流程及故障机理，系统总结了影响数控机床试验场可靠性试验评估修正系数的各项关键试验参数及过程状态监测量，并以此为基础，采用数据归一化方法，形成模糊评价选择集。

(2)针对快速可靠性试验评价中的修正系数影响因素多、存在模糊性、不能直接计算等特点，将试验数据、经验数据、评分系统等相结合，提出了一种基于模糊综合评价法的可靠性修正系数计算方法。

(3)以某国产数控立式加工中心为对象，采用试验场试验方式进行了可靠性加载试验与MTBF评估，并与5台同厂家同型号同年出厂机床现场跟踪试验MTBF评估结果进行对比，二者比较一致，验证了可靠性修正系数计算的准确性。

[参考文献]

[1] 杨兆军,陈传海,陈菲，等. 数控机床可靠性技术的研究进展[J]. 机械工程学报, 2013,49(20):130-136.

[2] JEFFREY P K，STEVEN M C，MARK E O，et al. Reliability of manufacturing equipment in complex environments[J]. Annals of Operations Research，2011，10: 1-26.

[3] 中国机械工业联合会. GB/T 23567.1数控机床可靠性评定 第1部分：总则[S]. 北京：中国标准出版社，2009.

[4] 黄祖广. 立式加中心可靠性测试与评价技术的研究[D]. 北京: 北京工业大学, 2007.

[5] 陈炳锟. 数控机床可靠性试验设计及评估方法研究[D]. 长春: 吉林大学, 2011.

[6] 李世龙. 数控机床可靠性评估及分配技术的研究[D]. 重庆: 重庆大学, 2013.

[7] Wang Y Q, Yam R C M, Zuo M J, et al. A comprehensive reliability allocation method for design of CNC lathes[J].Reliability Engineering and System Safety,2001,72(3):247-252.

[8] Zhang G B, Liao Z B. Research on Reliability Allocation of Direct-Drive Hobbing Machine[C]. 13th International Manufacturing Conference in China(IMCC2009).Materials Science Forum, 2009, v628-629: 245-250.

[9] Lee G L, Lin H J, Yu T W, et al. Optimal Allocation for Improving System Reliability Using AHP[C]. 2008 IEEE International Conference on Sustainable Energy Technologies(ICSET2008). Inst. of Elec. and Elec. Eng. Computer Society, 2008: 159-163.

[10] 郝庆波. 数控机床可靠性及维修性的模糊综合分配与预计[D]. 长春: 吉林大学, 2012.

[11] 张宏斌,贾志新,郗安民,等. 基于模糊综合评价的DK77系列电火花线切割机床可靠性评估[J].机床与液压, 2009, 37(11): 246-247.

[12] 于春雨,刘新华,李锋，等. 基于信息熵的小子样产品模糊可靠性评价方法[J]. 电测与仪表，2011, 48(546): 93-96.

[13] 黄祖广, 赵钦志, 盛伯浩，等. 加工中心可靠性试验载荷谱的研究[J]. 制造技术与机床, 2008 (2): 60-65.

[14] 曹国强，包明宇，高霁. 模糊综合评价法在复杂机械设备可靠性[J]. 机械设计与制造, 2003 (1): 1-2.

[15] 杨纶标，高英仪，凌卫新. 模糊数学原理及应用[M].广州：华南理工大学出版社，2011.

(编辑赵蓉)

The Calculation of NC Machine Tools Reliability Correction Factor

Based on Fuzzy Comprehensive Evaluation

XIA Yang-qiua,b, SHU Qianga,b,HU Qiua

(a. Institute of Mechanical Manufacturing Technology;b. Machine Tools Inspection and Evaluation Center, China Academy of Engineering Physics, Mianyang Sichuan 621900, China)

Abstract：In the evaluation of CNC machine tools reliability test, the correction coefficient is greatly affected by numerous factors and can’t be directly calculated and the affecting results is fuzzy, a calculation method for reliability correction coefficient based on fuzzy comprehensive evaluation is proposed. In this method, the key factors affecting the reliability correction coefficient are analyzed, the factor set obtained by experimental data normalization is established, the first level fuzzy comprehensive evaluation matrix is constructed by triangular membership functions, combined with expert scoring system, the final comprehensive evaluation matrix is formed, and by the maximum membership degree principle suitable for individual identification, reliability correction coefficient is judged. Reliability assessment test is performed on KVC1400B machining centers by Proving Ground test methods. The MTBF of the test is consistent with that of five same model machines for consecutive four-year field track statistics test, which suggests that fuzzy comprehensive evaluation can easily solve the problem of CNC machine tools reliability assessment correction coefficient calculation.

Key words：NC machine tools; reliability evaluation; correction coefficient; fuzzy comprehensive evaluation; scoring mechanism

中图分类号：TH161；TG506

文献标识码：A

作者简介：夏仰球(1987—)，男，江苏宿迁人，中国工程物理研究院工程师，硕士，研究方向可靠性工程、机床可靠性，(E-mail)xiayqiu@163.com；通讯作者：胡秋(1971—)，男，湖南双峰人，中国工程物理研究院高级工程师，工学硕士，研究方向为机电一体化系统设计集成测试，超精密加工设备研制，(E-mail)huqumaster@163.com。

*基金项目：四川省科技计划项目(2014GZ0119)；中国工程物理研究院技术基础科研基金(K846)

收稿日期：2015-03-14

文章编号：1001-2265(2015)12-0030-05

DOI:10.13462/j.cnki.mmtamt.2015.12.009