基于神经网络逆系统的机器人分数阶滑模控制*

徐庆宏，黄家才，周　磊

(南京工程学院 自动化学院，南京　211167)



基于神经网络逆系统的机器人分数阶滑模控制*

徐庆宏，黄家才，周磊

(南京工程学院 自动化学院，南京211167)

摘要：为提高工业机器人的控制性能，提出了基于神经网络逆系统的分数阶滑模控制方法。首先，使用BP神经网络逼近机器人的逆系统，实现了工业机器人系统的近似解耦线性化；考虑到工业机器人存在的不确定性和BP神经网络的逼近误差，将神经网络逆与工业机器人组成的复合伪线性系统等效为含有扰动的线性系统；在此基础上，基于滑模控制和分数阶微积分理论设计了分数阶滑模控制器，证明了闭环系统的稳定性。针对二自由度机器人多种不同工况的仿真研究表明了所提方法的有效性。

关键词：工业机器人；神经网络；逆系统；分数阶；滑模控制

0引言

随着科学技术的发展和人力成本的提升，工业机器人已逐渐被广泛应用于汽车、船舶、冶金等制造业领域。实现工业机器人高性能动静态特性的关键在于设计性能良好的控制算法。目前常用的工业机器人控制方法有阻抗控制[1-2]、逆系统控制[3]、自适应控制[4]、PID控制等，但上述方法在实际使用中往往具有一定局限性，如阻抗控制的控制精度依赖于操作者对环境知识的精确了解；逆系统控制方法依赖被控系统模型；自适应控制存在计算量较大、对于快时变系统实时性难以满足的不足，PID控制器参数难以整定等。

由于神经网络对连续非线性函数具有良好的逼近性能，文献[5]将神经网络与逆系统方法结合提出神经网络逆控制方法，并应用于工业机器人的解耦控制，克服了传统控制方法对机器人精确模型的依赖，取得了良好的控制效果。但是，现有的基于神经网络逆系统设计的闭环控制器大都是整数阶的，研究表明基于分数阶微积分理论设计的控制器，如分数阶PID控制器等，往往具有比对应的整数阶控制器更好的控制性能[6-9]。

滑模控制是一种具有良好鲁棒性能的控制方法，在非线性控制中得到了大量应用。将滑模控制与分数阶微积分结合，可以提高滑模面设计的灵活性，从而增加了控制器设计的自由度[8]。文献[8,10]研究了永磁同步电机的分数阶滑模控制，结果表明分数阶滑模控制可以获得良好的控制性能。但目前，分数阶滑模控制应用于机器人控制还鲜见文献。为提高工业机器人的控制性能，本文提出了基于神经网络逆系统的工业机器人分数阶滑模(FOSMC)控制方法，证明了闭环系统的稳定性，并通过数值仿真研究验证了所提方法的有效性。

1问题描述

对于一个n自由度关节的工业机器人机械手, 其动力学方程可表示为：

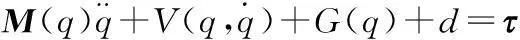
(1)

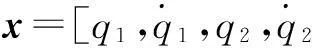
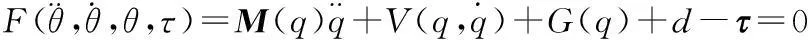
(2)

可得

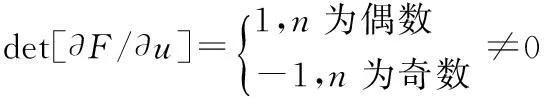
(3)

根据逆系统理论，工业机器人系统可逆，且逆系统可表示为

u=φ(x,v1,v2,...,vn)

(4)

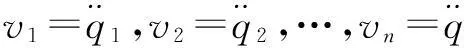
由于工业机器人在实际运行过程中往往存在参数变化等不确定性以及神经网络存在拟合误差，这使得神经网络逆与被控工业机器人系统构成的复合伪线性系统与理想的线性系统之间往往存在误差。考虑此误差，不妨将近似伪线性系统的输入输出描述为

(5)

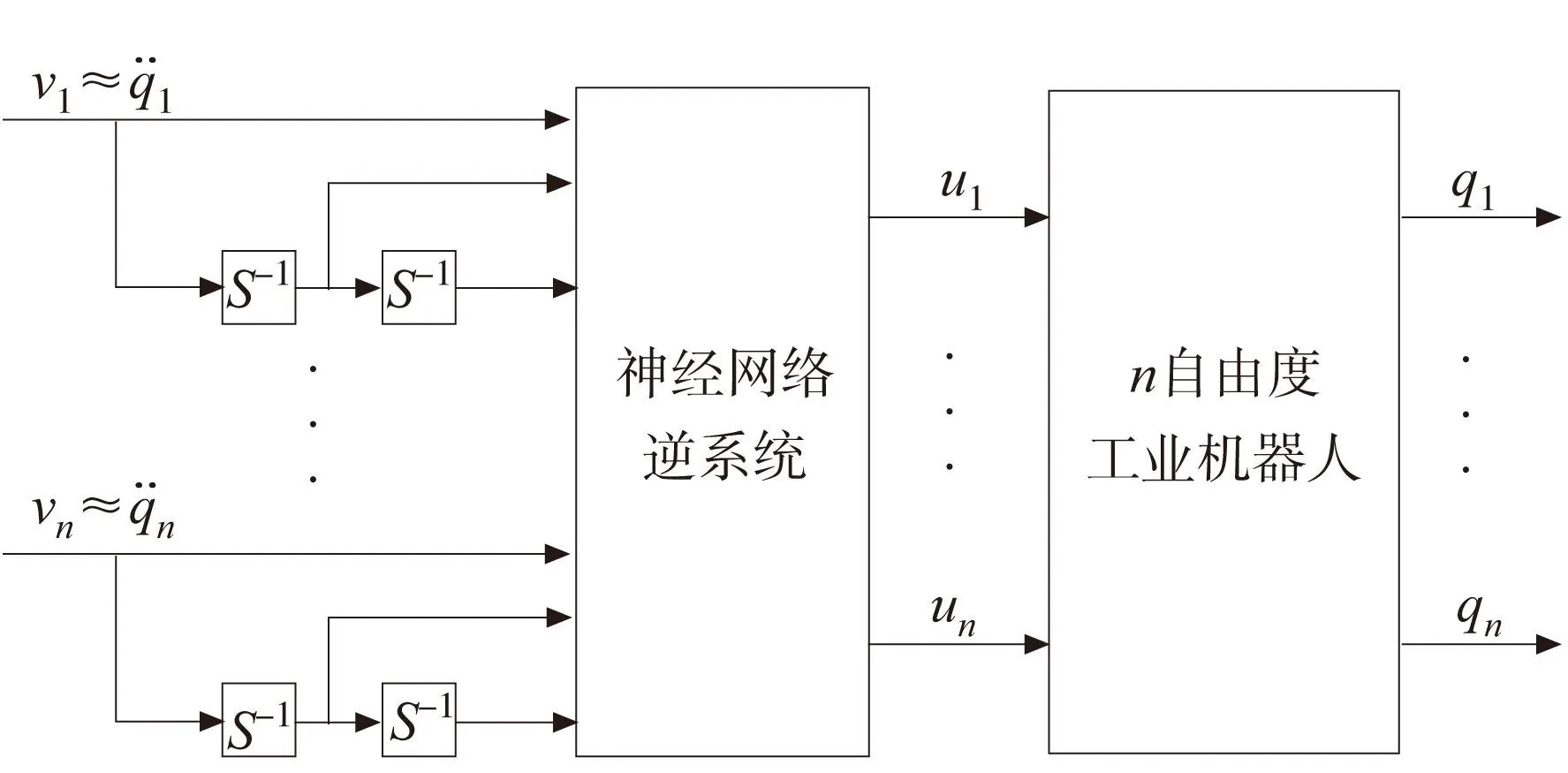
图1　基于神经网络逆系统的工业机器人近似解耦线性化原理图

2基于神经网络逆的分数阶滑模控制方法

针对神经网络逆系统与被控工业机器人所组成的伪线性复合系统，提出了基于神经网络逆的工业机器人分数阶滑模控制(FOSMC)方法，其原理图如图2所示。

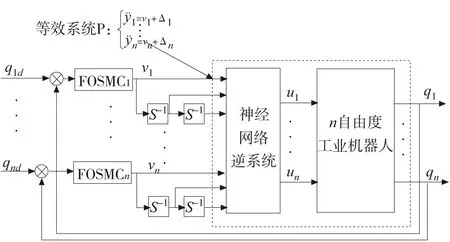
图2　基于神经网络逆系统的工业机器人分数阶滑模控制原理图

2.1神经网络逆系统设计

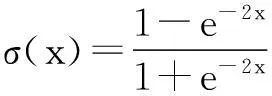
2.2分数阶滑模控制器(FOSMC)设计

针对神经网络逆系统与被控工业机器人组成的伪线性复合系统设计FOSMC。

设计滑模面为：

Si=kpixi1+kdiDμixi1=kpixi1+kdiDμi-1xi2

(6)

其中，μi∈(0,1)。

所以，有

(7)

定理：对系统(5)，当设计控制器

(8)

时，闭环系统稳定。

(1)当Si>0时，

kdiDμi-1(-εi-Δi-ki)<0

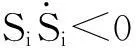
(2)当Si<0时，

kdiDμi-1(εi-Δi+ki)>0

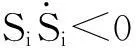
综上，定理成立。

为了减轻滑模控制中存在的“颤振”现象，本文在仿真中采用饱和函数sat代替符号函数sgn。具体为：

采用饱和函数的稳定性证明与采用符号函数的稳定性证明过程类似，限于篇幅，此处略去。

3数值仿真

针对一个二自由度工业机器人进行了数值仿真研究。

其中：

(9)

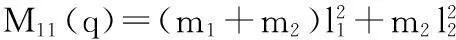
(10)

(11)

仿真中二自由度工业机器人的参数为：m1=10kg，m2=2kg，l1=1.1m，l2=0.8m，g=9.8m/s2。

施加不同组合的输入组合(τ1,τ2)对系统进行充分激励，数据采样间隔取为0.001s，每组输入组合的时间为5s。然后通过离线训练BP神经网络得到神经网络α=[2,2]阶右逆系统。BP神经网络逆系统的结构为6-13-2，最大迭代次数设置为5000次，均方差MSE目标为1×10-6，训练3000次精度满足要求，然后使用测试样本进行泛化能力检验后，将BP神经网络逆系统与工业机器人系统串联，构成相对阶α=[2,2]的近似伪线性系统。

针对机器人系统与神经网络逆系统组成的近似伪线性系统设计式(8)的闭环控制器为。其中，kp1=kp2=4,kd1=kd2=1,μ1=μ2=0.5,k1=k2=50，ε1=ε2=0.01。

针对多种工况进行了多组仿真，并与PID控制进行了比较研究。PID控制器经过多次试验后确定为PID1(s)= PID2(s)=300+30s。限于篇幅，这里给出部分结果。

工况1：对关节1施加一正弦信号q1d=10sint，对关节2施加一正弦信号q2d=10sin(2t)，控制效果如图3。

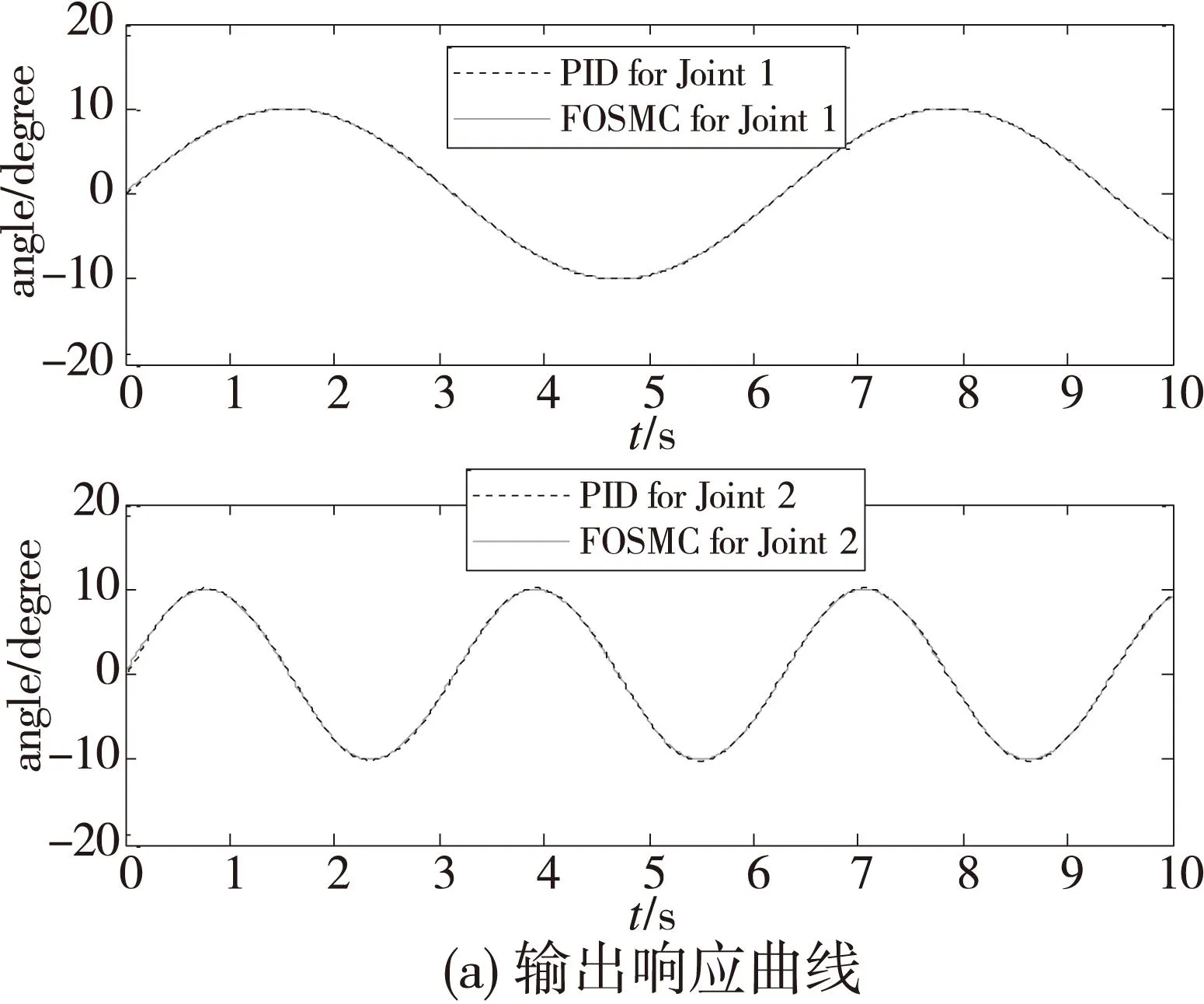
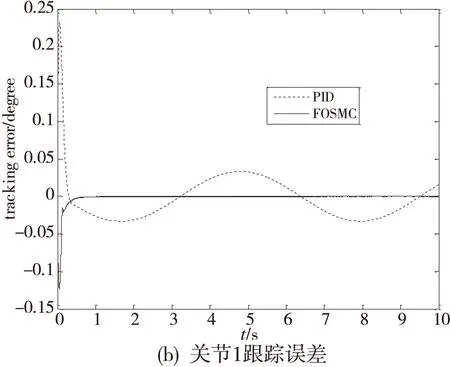
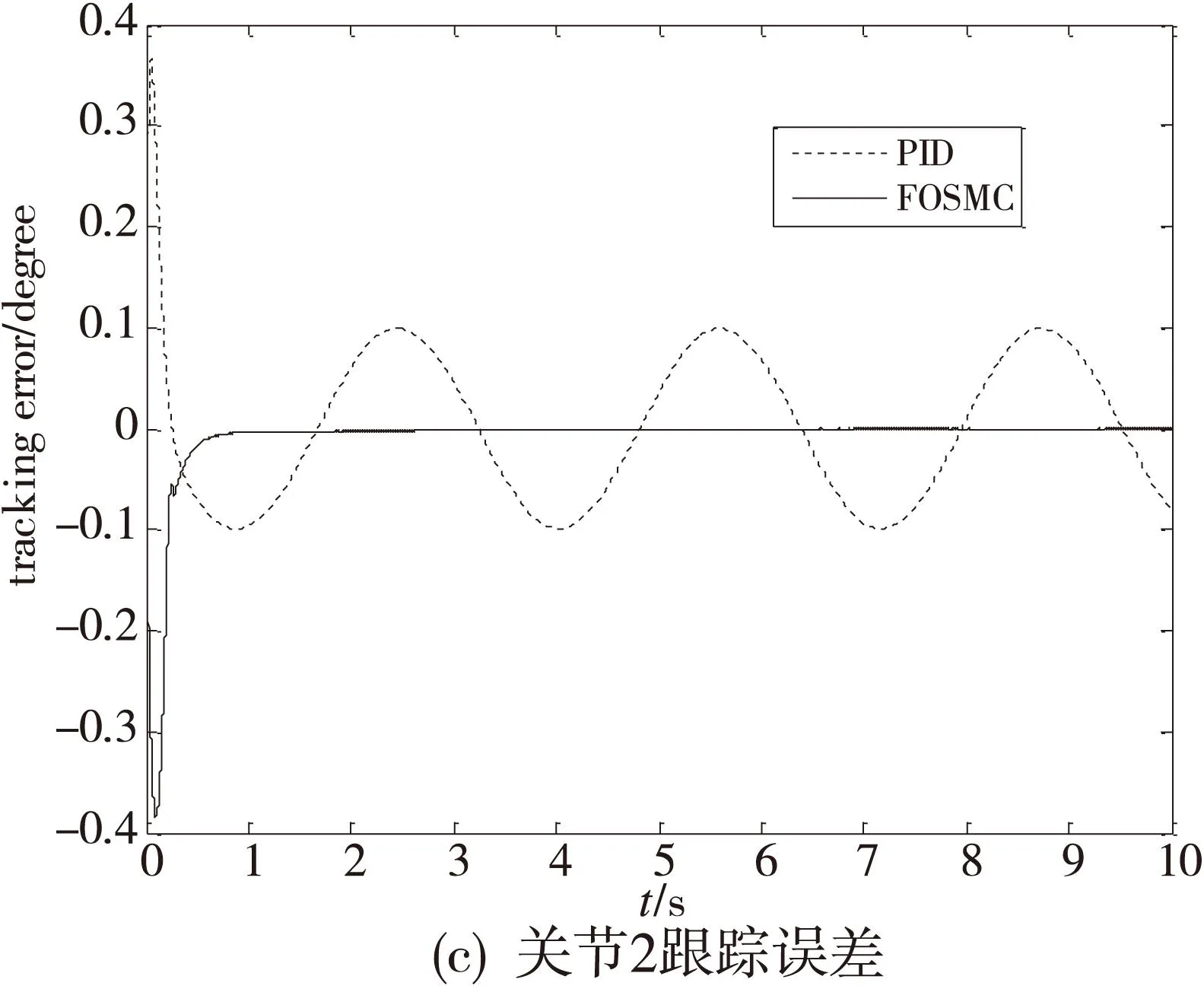
图3　二自由度机器人跟踪误差曲线

从图3的仿真结果可以看出，当无扰动时，本文所提出的基于神经网络逆系统的FOSMC方法可使机器人在1s内能快速跟踪给定输入，与PID控制方法相比较，可获得更好的控制性能。

工况2：对关节1施加一正弦信号q1d=10sint，对关节2施加一正弦信号q2d=10sin(2t)，同时在输出端对关节1和2分别增加扰动，d1=sin3t，d2=sin4t，控制效果如图4。

从图4的仿真结果可以看出，在有扰动情况下，本文所提出的基于神经网络逆系统的FOSMC方法可使机器人在1.5s内跟踪参考输入，较PID控制方法具有更好的跟踪性能。

因此可见，本文所提基于神经网络逆系统的FOSMC方法具有较好的鲁棒性。

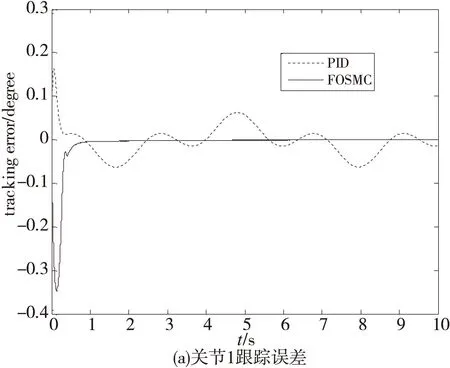
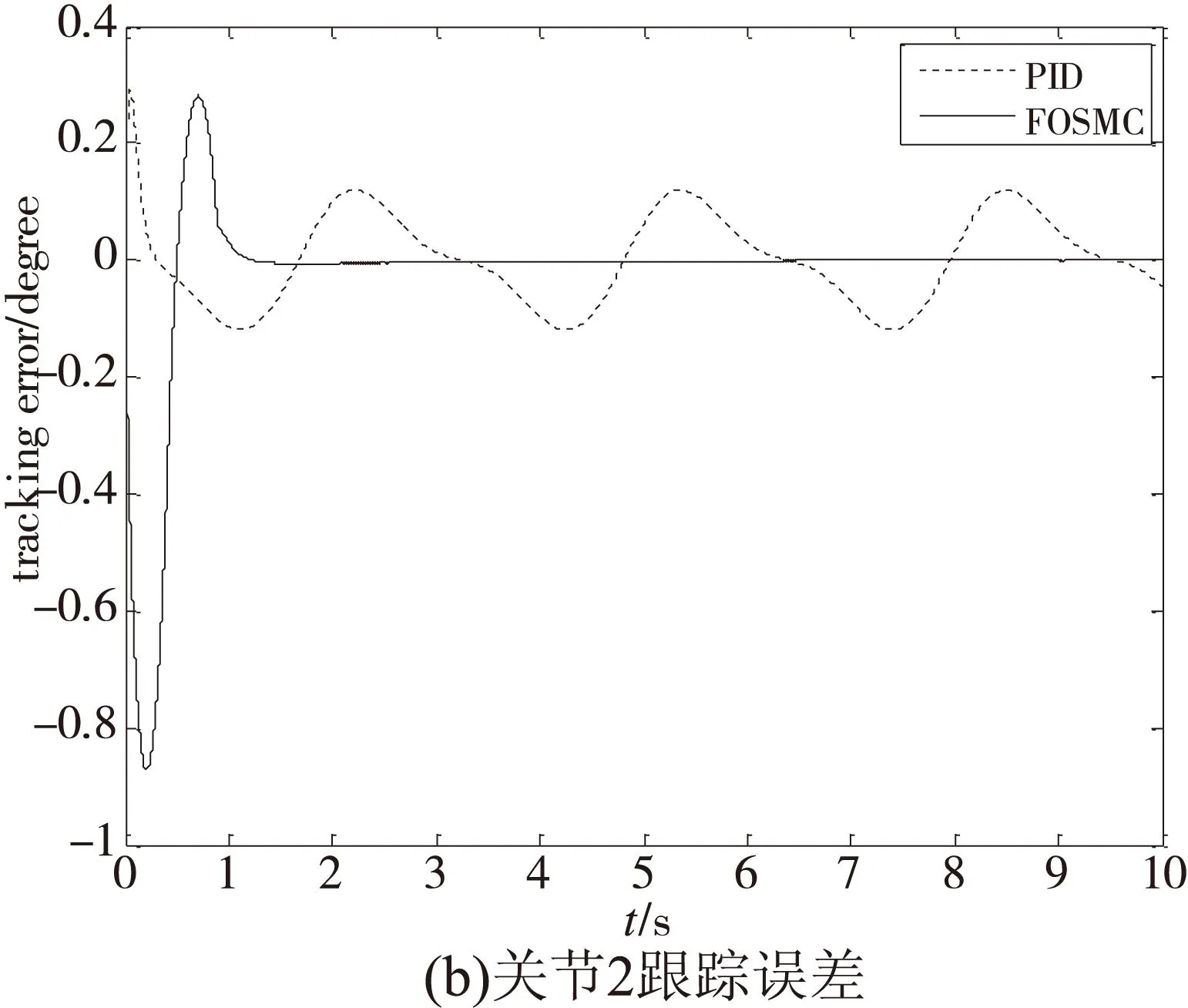
图4　二自由度机器人跟踪误差曲线

4结束语

针对工业机器人控制问题，提出了基于神经网络逆系统的FOSMC方法。使用神经网络逼近被控系统的逆系统，并将其与工业机器人组成复合伪线性系统；在此基础上针对伪线性复合系统设计了分数阶滑模控制器；针对二自由度机器人的数值仿真结果表明了所提方法具有良好的鲁棒控制性能。FOSMC控制方法

中的参数如何选取、优化是下一步的研究工作。

[参考文献]

[1] Caccavale F,Chiacchio P,Marino A,et al.Six-DOF Impedance Control of Dual-Arm Cooperative Manipulators[J]. IEEE/ASME Transactions on Mechatronics,2008,13(5): 576-586.

[2] 陈峰,费燕琼,赵锡芳. 机器人的阻抗控制[J].组合机床与自动化加工技术,2005(12):46-47.

[3] Lin Chen, Xingsong Wang, Xu W L. Inverse Transmission Model and Compensation Control of a Single-Tendon-Sheath Actuator[J]. IEEE Transactions on Industrial Electronics,2014,61(3): 1424- 1433.

[4] Pradhan S K,Subudhi B. Nonlinear Adaptive Model Predictive Controller for a Flexible Manipulator: An Experimental Study[J]. IEEE Transactions on Control Systems Technology,2014,22(5): 1754-1768.

[5] 戴先中,孟正大,沈建强,等.神经网络α阶逆系统控制系统方法在机器人解耦控制中的应用[J].机器人, 2001,23(4)：363-367.

[6] Concepción A Monje, Yangquan Chen, Blas M Vinagre, et al. Fractional-order Systems and Controls-Fundamentals and applications[M].Springer,2011.

[7] Li Hongsheng,Luo Y, Y Q Chen. A Fractional Order Proportional and Derivate(FOPD) Motion Controller:Tuning Rule and Experiments[J].IEEE Transactions on Control Systems Technology,2010,18(2):516-521.

[8] 张碧陶,皮佑国.基于模糊分数阶滑模控制的永磁同步电机控制[J].华南理工大学学报(自然科学版) ,2012,40(3):126-130.

[9] 吴忠强,王洋.分数阶不确定多智能体系统的鲁棒一致性控制[J].电机与控制学报,2013,17(4):97-103.

[10] Jiacai Huang,Hongsheng Li,YangQuan Chen,et al.Robust position control of PMSM using fractional-order sliding mode controller[J]. Abstract and Applied Analysis, 2012.

(编辑赵蓉)

ANN-inversion Based Fractional-Order Sliding Control for the Robot

XU Qing-hong, HUANG Jia-cai,ZHOU Lei

(School of Automation,Nanjing Institute of Technology,Nanjing 211167,China)

Abstract：To improve the control performance of the industrial robot, an ANN-inversion based fractional-order sliding mode control(FOSMC) scheme is proposed. Firstly, the BP neural network is used for the inversion of the industrial robot, and approximate decoupling and linearization of the industrial robot is got. Secondly, the composite pseudo linear system, which is composed of the ANN-Inversion system and the controlled industrial robot, is equivalent to a linear system with disturbance in view of the industrial robot uncertainties and the BP neural network’s approximation error. Then, the fractional-order sliding control(FOSMC) scheme is proposed based on the SMC theory and fractional calculus for the linear system with disturbance, and the stability analysis is given. Finally, case study is fulfilled for a two-DOF robot under different conditions, and results show the effectiveness of the proposed control scheme.

Key words：industrial robot; neural networks; inverse system; fractional caculus; sliding mode control

中图分类号：TH166；TG659

文献标识码：A

作者简介：徐庆宏(1979—)，男，南京人，南京工程学院讲师，博士，研究方向为智能控制，(E-mail)zdhxxqh@njit.edu.cn。

*基金项目：国家自然科学基金(61104085)；江苏省高校自然科学研究项目资助(13KJB510011)；南京工程学院校级科研基金项目资助(YKJ201218)

收稿日期：2015-03-07

文章编号：1001-2265(2015)12-0049-04

DOI:10.13462/j.cnki.mmtamt.2015.12.014