混凝土拉伸软化曲线确定方法的对比研究

赵志方，王　刚，周厚贵，王卫仑，潘存鸿

(1.浙江工业大学 建筑工程学院，浙江 杭州 310014；2.中国能源建设集团有限公司，北京100029；

3.广东省滨海土木工程耐久性重点实验室，广东 深圳 518060；4.浙江省水利河口研究院,浙江 杭州 310020)



混凝土拉伸软化曲线确定方法的对比研究

赵志方1，王刚1，周厚贵2，王卫仑3，潘存鸿4

(1.浙江工业大学 建筑工程学院，浙江 杭州 310014；2.中国能源建设集团有限公司，北京100029；

3.广东省滨海土木工程耐久性重点实验室，广东 深圳 518060；4.浙江省水利河口研究院,浙江 杭州 310020)

摘要：混凝土拉伸软化曲线(σ—w曲线)是评价混凝土断裂性能的重要指标.由σ—w曲线(简称软化曲线)，经数值模拟分析，就可预测混凝土结构的宏观断裂行为.采用三峡大坝混凝土的施工配合比，制作不同强度、骨料粒径的5组25个试件进行直拉断裂试验.基于直接拉伸试验结果和混凝土断裂力学分析，由直拉法确定混凝土的软化关系表达式.采用相同的材料和配合比制作5组20个楔入劈拉试件，测试其荷载—裂缝口张开位移(P—CMOD)曲线，并基于改进进化算法的逆推法确定混凝土软化曲线.对比分析逆推法和直拉法获得的软化曲线，验证用逆推法确定混凝土软化曲线的可行性.

关键词：直接拉伸试验;软化曲线;楔入劈拉试验;逆分析;进化算法

混凝土材料的非均质性使其裂缝尖端附近形成非线性的断裂过程区.虚拟裂缝模型(FCM)能较好描述裂缝尖端的物理特性，是目前模拟混凝土裂缝扩展的代表性模型.根据FCM模型，混凝土受拉时，开裂区的本构关系用应力—裂缝张开宽度(σ—w)曲线描述，即拉伸软化曲线.断裂能GF是软化曲线下的面积，它反映材料抵抗裂缝扩展的能力，是表达混凝土断裂性能和描述软化曲线的重要参数.

确定软化曲线的方法主要有二：一是用理想的直接拉伸试验[1-3],确定软化曲线.但对试验机要求高，需解决加载对中等难题，试验成本高，成功率低；二是基于简便断裂试验的逆推法[4-7]，由三点弯曲梁(TPB)或楔入劈拉(WS)试验测得P—CMOD曲线，通过数值模拟计算，逆推获得软化曲线.逆推法具有试验操作简便、省钱省时等优点，但其客观性受到争议.目前，有关逆推法和直拉法确定软化曲线的对比研究很少，因而将同时选用以上两种方法来进行对比分析.

1试验研究

1.1试件制作

试件形状如图1所示，混凝土配合比见表1.因直拉试验成功率较低，每组制作5个试件，保证每组有3个试件试验成功，试件尺寸均为B×D×L=150 mm×150 mm×300 mm.楔入劈拉试件每组制作4个，试件尺寸B×D×L=200 mm×300 mm×300 mm，初始缝长a0=150 mm，缝宽2 mm.试验龄期为1 年.

图1　试件形状示意图Fig.1　Sketch of specimens shape

直拉试件组别楔入劈拉试件组别水胶比最大骨料粒径/mm每方材料用量/kg水水泥粉煤灰石子人工砂引气剂减水剂DT[2]WS[2]0.50101401968410908690.01961.680DT[3]WS[3]0.50401201687212877690.01681.440DT[4]WS[4]0.50201321857911528460.01851.584DT[5]WS[5]0.45201352406011548140.01951.800DT[6]WS[6]0.30201404204711216980.02802.802

1.2基本力学性能试验

按照DL/T5150—2001《水工混凝土试验规程》[8]测试同批次混凝土的150 mm×150 mm×150 mm立方体抗压强度fcu及劈裂抗拉强度fts，φ150 mm×300 mm圆柱体抗压强度fc、弹性模量E和泊松比γ，结果见表2.

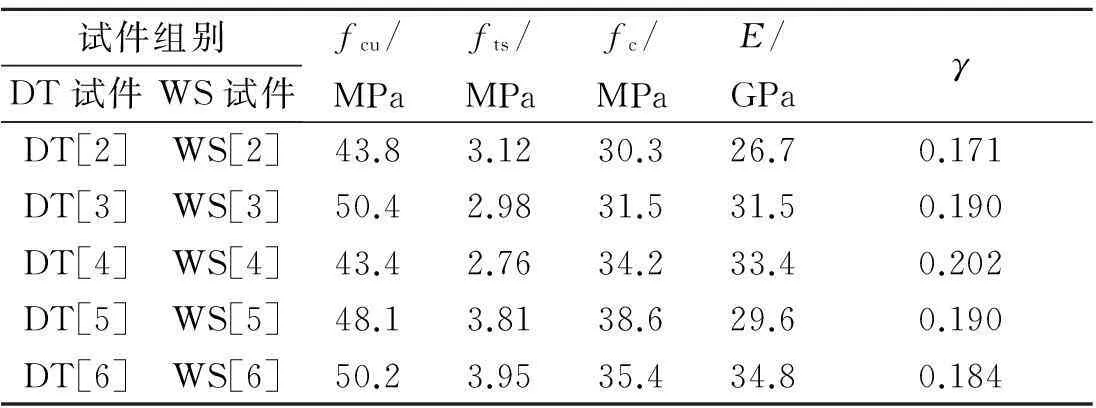
表2　基本力学性能试验结果

1.3直接拉伸试验

DT试验采用刚度为6 000 kN/mm的Instron 8506大刚度电液伺服闭路试验系统.测试系统带有上下两个球形铰，负载达3 000 kN.球形铰的偏转角均为20度，从而保证相对的偏心度小于10%.试验前48 h，用环氧树脂将试件和上下两个端板相粘结.当结构胶达到强度时，将试件和上、下球铰相连接，以保证试件轴向对中.为测量轴向变形，在试件每侧各放置1个位移计，量程为±5 mm，精度为±0.002 mm.在整个试验过程中，采用5 μm/min的速率进行应变控制加载，以使直拉试验稳定进行.采用计算机控制加载和数据采集，加载的同时，观察裂缝的发生与扩展.

1.4楔入劈拉试验

楔入劈拉试验采用位移控制加载，加载速率为0.15 mm/min.位移传感器的精度5 μm，量程5 mm.采用两台DH5937型号的应变测试系统记录试验数据，直到试件完全断开.

由WS试验，可以测得试件的荷载—裂缝口张开位移(P—CMOD)曲线.

2直拉法确定混凝土的软化曲线

以直拉试件组DT[3]为例，说明确定σ—w曲线的方法.经DT试验，获得试件的以下成果：

1) 直拉应力—变形曲线(σ—δ曲线)，见图2.

图2　试件组DT[3]σ—δ曲线Fig.2　σ-δ curves of specimen group DT [3]

2) 直拉应力σ和裂缝张开宽度w的关系曲线(σ—w曲线).

图3为σ—δ曲线示意图.在DT试验中，试件的总变形δ由三部分组成：

δ=δ0+w+δe

(1)

式中：δ0为残余变形；w为虚拟裂缝张开宽度；δe为试件的弹性变形.残余变形为

δ0=δp-δep

(2)

式中：δp为峰值点处试件总变形；δep为峰值点处试件的弹性变形.弹性变形δe计算式为

δe=σl/E

(3)

式中：l为试件长度；σ为某时刻的应力；E为弹性模量.则根据DT试件的σ—δ曲线，可求得裂缝张开宽度w为

w=δ-δe-δ0

(4)

DT[3]试件组各试件的σ—w曲线如图4所示.

图3　混凝土应力—变形曲线示意图Fig.3　Sketch of stress-deformation curve of concrete

图4　试件组DT[3]σ—w曲线Fig.4　σ-w curves of specimen group DT [3]

根据虚拟裂缝模型，软化曲线表征断裂过程区的裂缝张开宽度w和粘聚应力σ之间的关系.当σ降为0时，虚拟裂缝达到最大裂缝宽度wc，开始出现“宏观裂缝”[9].

对同组试件的σ—w曲线数据的最小二乘拟合结果，直拉试件组DT[3]的ft=2.341MPa，wc=1.22mm，GF=401.4N/m.采用最小二乘法得到软化关系表达式为

(5)式中φ，λ，n为材料参数，对于试件组DT[3]：φ=1.20，λ=0.030，n=0.48，R2=2.3(R2为拟合相关指数).同理亦可求所有试件组混凝土的软化关系表达式，控制参数见表3.

表3　直拉法确定的软化曲线参数

3逆推法确定混凝土的软化曲线

3.1基于进化算法的逆推法

逆推法：先根据经验假定σ—w曲线，经有限元模拟计算求得P—CMOD曲线，再和WS试验实测数据对比.通过不断更新假定的曲线使得计算结果与实测数据吻合，就可确定混凝土的σ—w曲线.在逆分析计算过程中，优化算法的选择对计算的效率和结果有很大的影响.采用传统优化算法时，存在着多重局部最优解的弱点.进化算法(EA)是一种高效的随机搜索方法，它从串集开始搜索，有效的避免了局部最优解[5].

逆分析计算的有限元程序流程图见图5，采用三段线性软化曲线形式.

图5　逆分析计算流程图Fig.5　Flow chart of inverse analysis calculation

WS试件为对称结构，取试件的一半建模分析计算.采用虚拟裂纹模型(FCM)和Gopalaratnam[10]提出的叠加原理来模拟裂缝的扩展.如图6所示，沿裂缝扩展路径设置铰约束.当混凝土的拉应力达到抗拉强度ft时，该结点铰约束释放.裂缝扩展的过程通过沿扩展方向由上往下逐个释放铰约束来实现，同时获得相应的外荷载和位移值.

图6　基于FCM模型模拟混凝土裂缝扩展Fig.6　Crack extension simulation of concrete based on the FCM

3.2逆推计算结果

文献[11]建议将每组试件实测的P—CMOD曲线处理成一条有代表性的曲线.但是同组各试件的实测P—CMOD曲线存在差异.故笔者单独计算每个试件的σ—w曲线，然后平均和拟合处理同组试件的σ—w曲线，获得该组试件的软化曲线.

基于实测的P—CMOD曲线，可按以上逆推法获得每个试件的σ—w曲线.图7为WS2-1模拟计算的P—CMOD曲线与试验实测曲线的对比图.

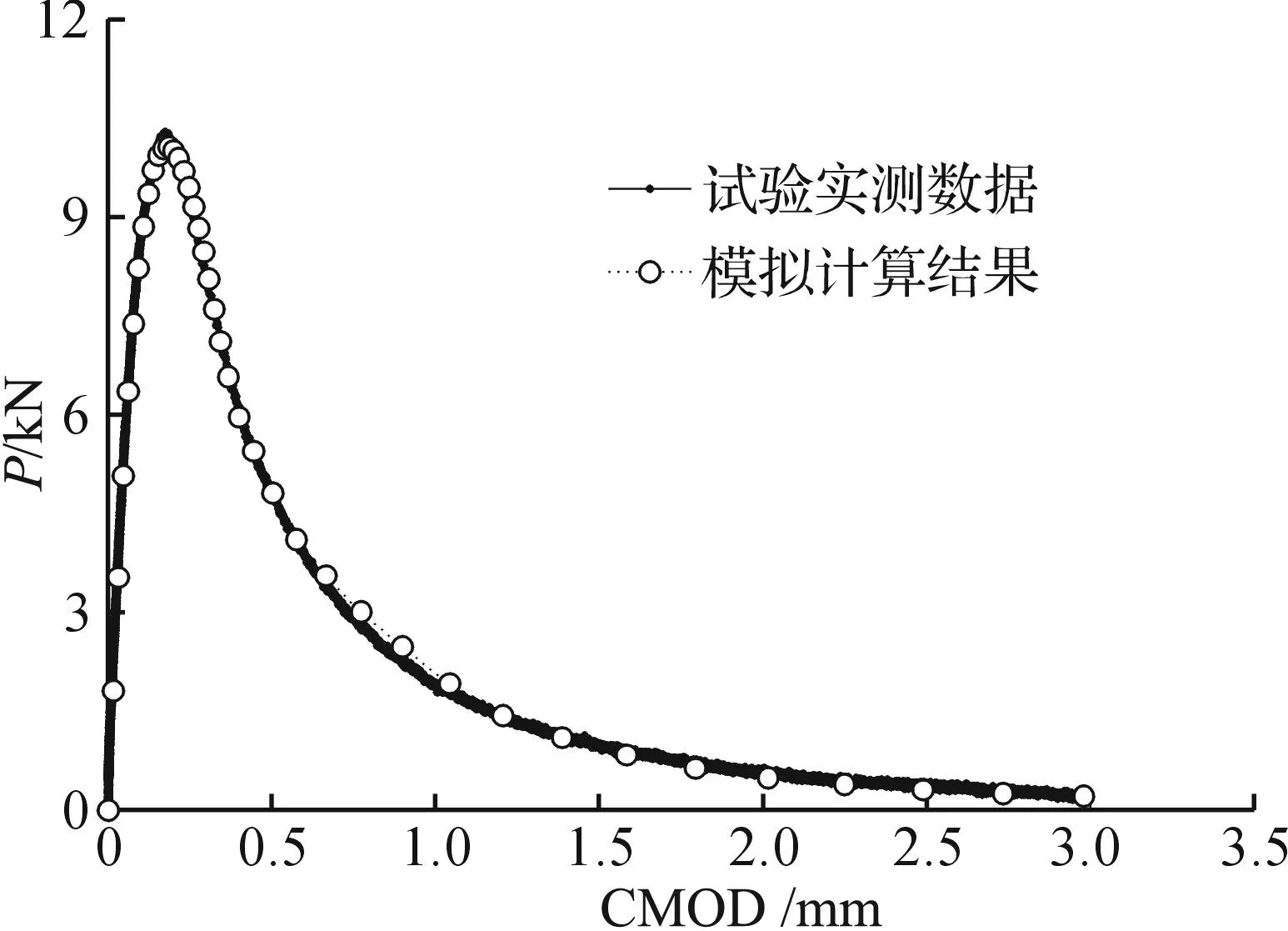
图7　WS2-1模拟计算的和实测的P—CMOD曲线对比图Fig.7　Comparison between calculated and tested P-CMOD curve of WS2-1

逆推法得到的各试件P—CMOD曲线的峰值荷载Pmax以及峰值处的裂缝口张开位移值CMODc与相应实测数据对比如图8所示，斜线为45°线.

图8　逆推法计算的和实测的Pmax以及CMODc值的对比Fig.8　Comparison of Pmax and CMODc between calculated and tested values

可以看到：经由有限元模拟计算的P—CMOD曲线和实测结果吻合良好，可见采用改进进化算法的逆推法可较好地获得每个试件的σ—w化曲线.

同组试件的σ—w曲线平均和拟合的方法如图9所示.为简便说明问题,以两条软化曲线为例,阐明软化曲线平均和拟合的过程.

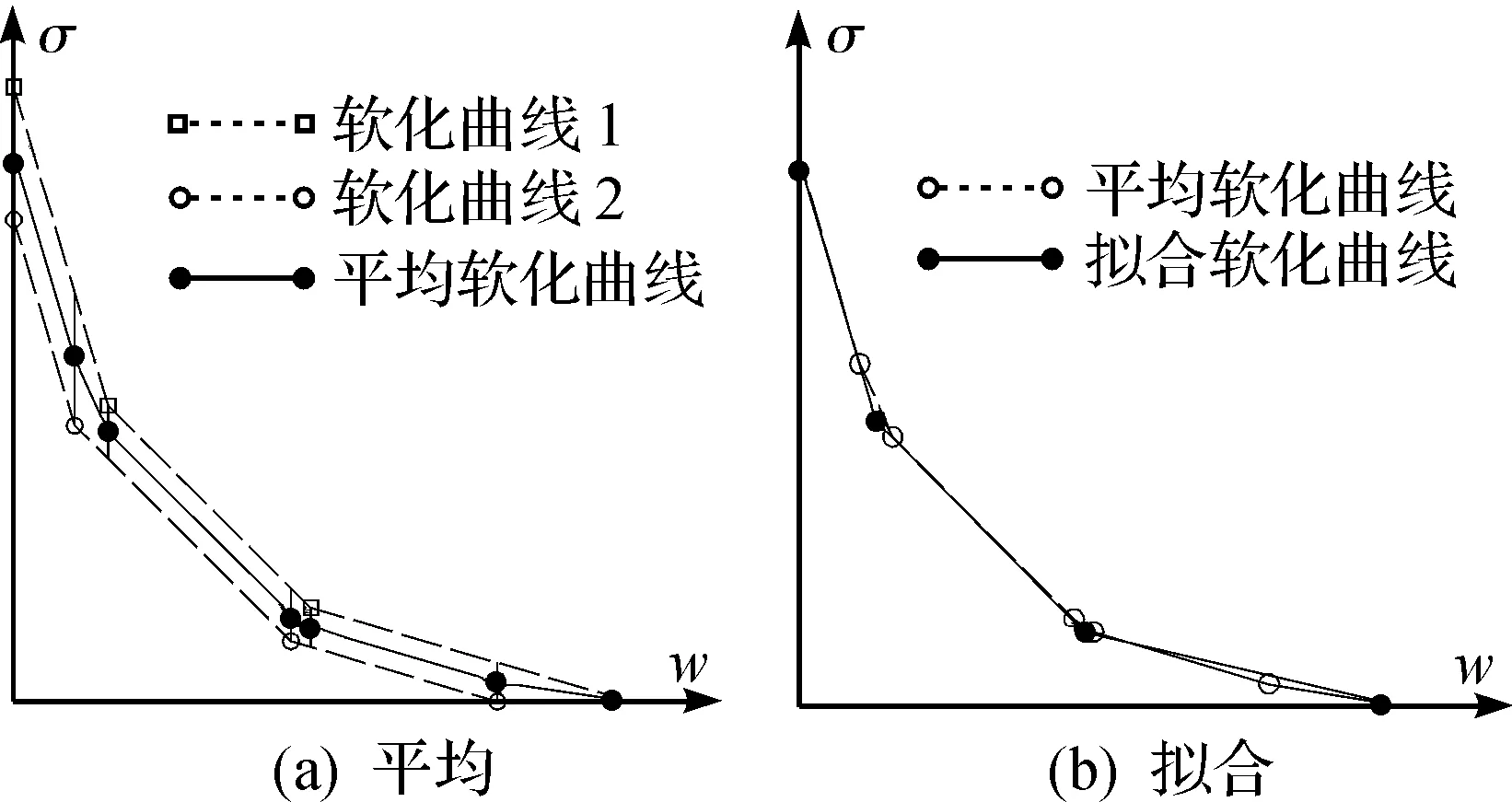
图9　σ—w曲线的平均和拟合Fig.9　Averaging and fitting of σ-w curves

如图9(a)所示，软化曲线的平均是将每条σ—w曲线拐点处所对应的σ值平均.把平均后的曲线(称为“平均软化曲线”，实际为1条六段线性软化曲线)再拟合成1条三段线性的曲线，如图9(b)所示.软化曲线拟合本质是保证“平均软化曲线”和拟合的三段线性软化曲线下的面积相等，同时使两者尽可能吻合.逆推法得到的各试件组的软化曲线见图10.

4逆推法与直拉法获得的软化曲线对比

所采用的DT试件和WS试件具有相同的断裂韧带高度(150 mm)，WS试件逆推获得的软化曲线与相应配合比的DT试件对比如图10所示.

可以看到：两种方法获得的混凝土软化曲线基本吻合，而且得到的表征混凝土断裂性能的重要参数GF吻合良好，可认为笔者采用两种方法所获结果基本一致.因而，基于楔入劈拉试验的逆推法可为大坝混凝土软化曲线的确定提供参考.由逆推法获得的抗拉强度ft偏大,可能是由于两种试件的形状尺寸以及加载方式的不同，且受模型简化的影响，具体原因有待进一步研究.

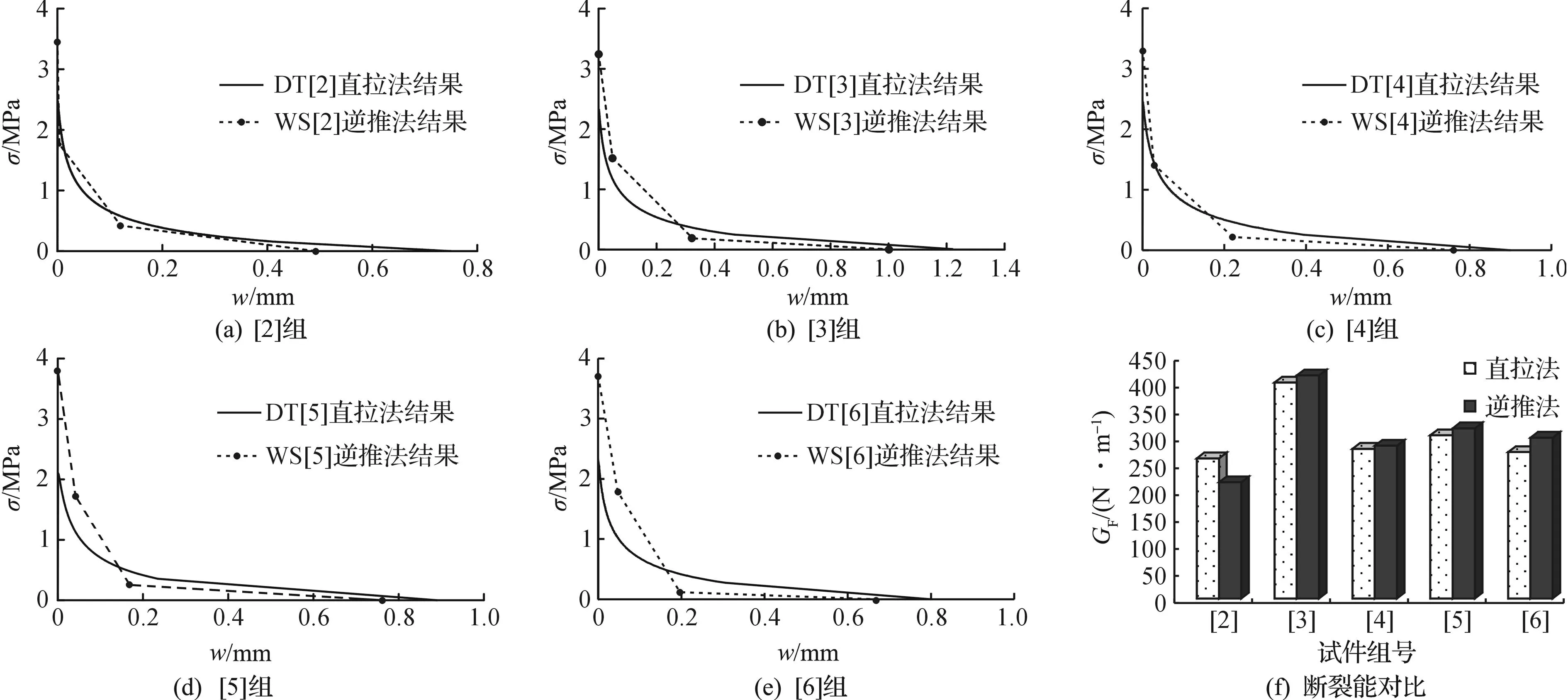
图10　逆推法与直拉法确定的软化曲线对比图Fig.10　Comparison of softening curves between inverse analysis and direct tension method

5结论

为研究混凝土的软化特性，在三峡大坝施工现场采用其原材料与养护条件仿真制作不同配合比、骨料粒径的直拉试件以及相应的楔入劈拉试件.基于直拉试验结果和断裂力学分析得到混凝土的软化关系表达式；基于楔入劈拉试验实测的P—CMOD曲线，采用改进的进化算法，由逆推法获得混凝土的拉伸软化曲线.两种方法所获得的软化曲线基本一致,且断裂能吻合良好，从而验证了采用改进进化算法的逆推法的可行性，为探索基于简便断裂试验确定混凝土软化曲线提供新的思路.

致谢：衷心感谢清华大学李庆斌教授和德国Volker Slowik教授对本研究的指导.

参考文献：

[1]GOPALARATNUM V S, SHAH S P. Softening response of plain concrete in direct tension[J]. ACI Materials Journal,1985,82(3):310-323.

[2]LI Qingbin, ANSARI F. High strength concrete in uniaxial tension [J]. ACI Materials Journal,2000,97(1):49-57.

[3]ZHAO Zhifang, ZHANG Jun, ZHOU Hougui, et al. Two methods for determining softening relationships of dam concrete and wet-screened concrete[J]. Advances in Structural Engineering,2012,15(7):1125-1138.

[4]KITSUTAKA Y. Fracture parameters by polylinear tension-softening analysis[J]. Journal of Engineering Mechanics,1997,123(5):444-450.

[5]SLOWIK V, VILLMANN B, BRETSCHNEIDER N, et al. Computational aspects of inverse analyses for determining softening curves of concrete[J]. Computational Methods in Applied Mechanics and Engineering,2006,195:7223-7236.

[6]KWON S H, ZHAO Zhifang, SHAH S P. Effect of specimen size on fracture energy and softening curve of concrete part Ⅱ: inverse analysis and softening curve[J]. Cement and Concrete Research,2008,38(8/9):1061-1069.

[7]冯孝杰.大体积混凝土软化曲线的新确定方法[D].杭州：浙江工业大学，2012.

[8]中华人民共和国国家经济贸易委员会.DL/T5150—2001水工混凝土试验规程[S].北京：中国电力出版社,2002.

[9]赵志方,宋柳林,周厚贵,等.大坝和湿筛混凝土起裂荷载的确定方法[J].浙江工业大学学报,2014,42(4):355-358.

[10]GOPALARATNAMA V S, YE B S. Numerical characterization of the nonlinear fracture process in concrete[J]. Engineering Fracture Mechanics,1991,40(6):991-1006.

[11]ZHAO Zhifang, KWON S H, SHAH S P. Effect of specimen size on fracture energy and softening curve of concrete part Ⅰ: experiments and fracture energy[J]. Cement and Concrete Research,2008,38(9)：1049-1060.

(责任编辑：陈石平)

A comparative study of methods for determining

the tensile softening curve of concrete

ZHAO Zhifang1, WANG Gang1, ZHOU Hougui2, WANG Weilun3, PAN Cunhong4

(1.College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China;

2.China Energy Engineering Group Co. Ltd., Beijing 100029, China；

3.Guangdong Provincial Key Laboratory of Durability for Marine Civil Engineering, Shenzhen 518060, China；

4.Zhejiang Institute of Hydraulics & Estuary, Hangzhou 310020, China)

Abstract:The tensile softening curve (σ-w curve) of concrete is an important index for evaluating the fracture properties of concrete. The macroscopic fracture behavior of a concrete structure can be predicted by numerical simulations with the tensile softening curve. A direct tension test was conducted on 25 dam concrete specimens in four groups made with different strengths and diameters of coarse aggregate using the construction mix proportions of the Three Gorges dam project concrete. Based on the direct tension test data and the analysis of fracture mechanics of concrete, the expressions for the softening curves were obtained. A total of 20 wedge-splitting specimens in five groups were made using the same materials and mix proportions as those of direct tension specimens. The load-crack mouth opening displacement (P-CMOD) curves were measured and the softening curves of concrete were obtained by the inverse analysis method of an improved evolutionary algorithm. A comparison of softening curves obtained from the inverse analysis method and the direct tension method was made to verify the validity of the inverse analysis method.

Keywords:direct tension test; softening curve; wedge-splitting test; inverse analysis; evolutionary algorithm

文章编号：1006-4303(2015)04-0455-05

中图分类号：TV313

文献标志码：A

作者简介：赵志方(1970—)，女，河南洛阳人，教授，博士，研究方向为大体积混凝土断裂力学，E-mail:zhaozhifang7@126.com.

基金项目：国家自然科学基金资助项目(51479178，51278304)；浙江省自然科学基金资助项目(LY14E090006)；广东省滨海土木工程耐久性重点实验室开放基金资助项目(GDDCE 14-01)

收稿日期：2015-01-30