带显著性区域约束的高效视频全景拼接方法

带显著性区域约束的高效视频全景拼接方法

范菁，吴佳敏，叶阳，吴冬艳，王浩

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

摘要：传统的基于流形的全景拼接技术在处理包含局部运动的视频时，存在不能保留特定关键区域的内容、表达视频运动信息的能力较差以及实现速度较慢的问题.针对上述问题，提出了一种带显著性区域约束的高效视频全景拼接方法，该方法在基于流形的视频拼接的基础上考虑图像的特征点，通过设定显著性区域，生成关键帧带约束的全景图；然后对关键帧全景图进行对齐及融合，构建运动全景图；并采用基于CUDA的并行计算方法进行算法加速.实验结果表明：该方法不仅可以在全景图中保留特定对象某一时刻的具体形态，而且可以保留运动对象多个运动形态，并且有较快的拼接速度.

关键词：视频拼接；流形；特征点；全景图；对象约束；CUDA技术

收稿日期：2015-04-15

基金项目：浙江省重大科技专项项目(2013C01112,2012C01SA160034)；杭州市重大科技创新专项(20132011A16)

作者简介：范菁(1969—)，女，浙江杭州人，教授，博士生导师，研究方向为虚拟现实与软件中间件等，E-mail:fanjing@zjut.edu.cn.

中图分类号：TP391

文献标志码：A

文章编号：1006-4303(2015)05-0479-08

Abstract:The traditional panorama stitching technique based on manifold can’t retain the contents of particular key areas in videos. The ability to express the motion information of video is poor and the speed is slow. In order to solve these problems, an efficient panoramic stitching method with significant region constraint is presented. Based on the manifold video stitching and the image feature points, this method will set significant area to generate the panorama with constraint for key frames firstly. Then the panoramas in the key frames are aligned and fused to obtain the motion panorama. The CUDA parallel computing is used to speed up. The experimental results showed that the proposed method can not only retain the specific form of specific object at a certain moment, but also can keep multiple movement patterns of moving objects in the panorama. It can effectively improve the speed of image stitching.

Keywords:video stitching; manifold; feature points; panorama; object constraint; CUDA

An efficient panoramic stitching method with significant region constraint

FAN Jing, WU Jiamin, YE Yang, WU Dongyan, WANG Hao

(College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China)

视频作为影视娱乐、信息传播或场景监控的载体，已在日常生活和工业应用中发挥重要的作用.随着视频资源数量的增加和计算机技术的发展，人们对视频分析及处理的要求越来越高[1].视频全景拼接技术通过对持续时间较长的视频提供简短的概括性摘要，帮助用户快速了解视频的大致内容，提高了分析和处理视频信息的效率.但是在处理包含运动对象的视频时,由于运动对象在视频中的每个时刻位置和形态都不同，简单的全景拼接技术只是将一段视频拼接成一幅涵盖场景全貌的高分辨率图像，无法保证运动对象的完整性，更无法满足在全景图构造时保留特定对象某一时刻形态的需求.

目前视频领域比较经典并被广泛使用的方法是基于流形思想的拼接方法[2]，该方法通过在时空立体空间下的流形投影，以像素列为基本单位进行拼接操作；但是此算法要求视频帧之间存在对齐关系，只适用于内容为静态场景的视频对象.为了适应运动视频的特性，Zomet等[3-4]针对基础算法要借助摄像机位置的改变来合成全景图像的缺点，提出一种适用于多种摄像机运动的通用方法，但是影响了算法速度.Rav-acha等[5]针对随机运动的视频引入时空空间概念，但是无法处理具有结构性运动的视频.Wexler等[6]则提出了一种较为完整的基于时空场景的流行拼接算法，不需要对像素列作对齐操作，也允许视频场景中包含局部运动，但是其合成的全景图并不包含视频详细内容，而且处理速度也由于应用Dijkstra算法而减慢.张树江等[7]改进了像素列间距离的定义，提出了一种改进的基于流形的全景图绘制方法，可以构建更完整详细的全景图，但同时也增加了计算复杂度.Hu等[8]针对实时交通监控视频，采用基于流形的图形拼接的算法并改进像素列之间的距离计算，但是算法的适用场景较局限.郭李云等[9]则在场景流形的拼接算法中对长视频采用分段处理的方式，虽然该方法能较快得到质量较高的全景图，但没有考虑运动视频全景图的特殊需求.综上所述，基于流形思想的视频拼接技术已经有了较深入的研究，但是运动视频全景图的构建效果及算法处理速度还有待提高.因此，针对以上问题，笔者提出了一种带显著性区域约束的高效视频全景拼接方法，该方法在基于流形的视频拼接的基础上进行视频显著性区域的划分，形成对象约束的全景图，然后通过对关键帧的全景图进行图像融合，形成运动全景图，最终实现了多运动形态显示和特定对象特定时刻的具体形态展现.同时，该方法采用CUDA并行计算，显著提升了拼接速度.

1带显著性区域约束的全景拼接技术

视频是图像序列的集合，参照基于时空场景的流行拼接算法[6]，我们将一段视频的图像序列投射于三维坐标系中，形成一个时空立体空间(图1).此空间中，X轴为图像的宽度，Y轴为图像的高度，T轴是视频图像的时间方向，因此单张视频图像即可视为一个二维平面(X—Y)，全部图像可以对齐到时间T轴.

图1　视频立体空间 Fig.1　Video stereo space

若要从视频图像序列中抽象出一幅场景过渡自然、无拼接痕迹的新图像，就需要从大量的像素列集合中挑选出适合的拼接像素，而如何挑选像素就是一个寻找贯穿整个立体空间最佳流形切面(Y—T平面)的问题，在时间轴上获得的该二维剖面的投影就是视频的全景图像，即图1中边缘线所标出的二维剖面.因此，需要确定流形切面的最优性以及寻找这个最佳剖面.

1.1功能函数

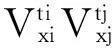
(1)

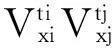
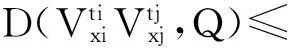
(2)

式(2)可简化为

(3)

所以，最优路径中各像素列之间的总和可以定义为

(4)

1.2构图过程

图2　相邻结点的取值范围 Fig.2　Value range for nearby node

(5)

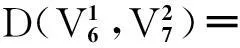
(B-B′)2)

(6)

求解最短路径采用的是Dijkstra算法.经典的Dijkstra算法主要用来求解单源、无负权的最短路径，其时间复杂度为O(V×V+E)，V为结点数，E为边数.假定源节点为s，不包括源结点的结点集合为V.搜索算法的基本思想是：先设定源节点到V中所有结点的长度为无穷大，即Initial过程；然后每次从集合V中取出当前情况下到源节点s的最短结点u，即ExtractMin过程；最后对u的相关边进行松弛更新，即Relax过程[10].

1.3对象约束的全景拼接

对于不存在局部运动的视频，每一帧图像中显著对象本身不会发生变化，因此利用功能函数及构图过程的思路寻找到时空立体空间的下一条最优路径就可以实现简单的全景图拼接；但是，若视频存在局部运动的对象，根据以上方法则无法在全景图中包含运动对象的某一刻形态.针对以上问题，考虑存在局部运动的视频全景拼接，提出一种对象约束的全景拼接思想.

由于存在局部运动的对象是肉眼马上能感知到的，所以我们对视频帧的重要度定义可以增加一个显著性判定标准：是否存在运动的对象，包含运动对象的区域可以定义为视频帧的显著性区域.然后，用户指定全景图中包含哪一帧的显著性区域，通过这种对象约束生成带约束的全景图.

在获取显著性区域的过程中，首先采用光流法[8]来提取视频中的运动对象.光流法能实现复杂运动目标的检测和跟踪，而且克服光亮度变化的影响[11].在得到每帧图像的光流场信息后，把该运动信息按式(7)转换成光流信息可视化图.

(7)

其中：vx为x方向的速度；vy为y方向的速度.

对光流信息可视化图进行二值化和形态学操作，找出图中灰度值出现0值的最左边的像素和最右边的像素，并对其x轴上的位置进行记录：左边位置记为左边界left_x，右边位置设为右边界right_x.最后，将left_x～right_x区域范围内的图像置为显著性区域；图3中框标记为视频图像的显著性区域.

图3　视频图像显著性区域 Fig.3　The significant area of a video image

从左边界left到右边界right的区域中的每一列像素可作为带约束的最短路径中的必经结点.该区域中的所有必经结点构成一段必经路径.从源节点到目标结点的最终路径中，需要包含这一段路径.那么最终的最短路径可以分成3部分：1) 从源结点到left的最短路径；2) 必经路径；3) 从right到目标结点的最短路径.这三部分最短路径组成的路径，即为符合实际情况的最短路径，公式可定义为

Pmin=P(s,l)+P(l,r)+P(r,f)

(8)

其中：P表示路径；Pmin为最终的最短路径；s为源节点；l为左边界；r为右边界；f为目标结点.

根据以上思路分别对两段运动视频mashu.avi和jieli.avi进行实验，实验结果如图4，5所示.图4(a)和图5(a)分别为两段视频中的部分原始帧；图4(b)和图5(b)为不带约束的视频全景图拼接图；图4(c)为保留图4(a)中mashu.avi视频序列第4张图片中马的动作生成的带约束的全景拼接图；图5(c)为保留jieli.avi视频序列的第1张图片中运动员的动作生成的带约束的全景拼接图.

图4　mashu.avi视频的拼接结果 Fig.4　Video panorama stitching results of mashu.avi

图5　jieli.avi视频的拼接结果 Fig.5　Video panorama stitching results of jieli.avi

基于以上思路，我们也可以对其他帧的显著性区域进行检测并标记，然后在全景图中保留该部分显著性区域.实验结果表明：采用该算法能够获得单独的不同姿势的全景图.但该算法有一个不足之处，就是在全景图中不能详细显示运动对象的运动状态，即同时保留多个姿势实现包含多对象的全景图，这就是我们下面要研究的问题.

1.4多形态运动对象的全景图生成方法

为了使全景图能够完全显示运动对象在视频中的概况，可以采用一种基于流形的视频拼接和基于特征点图像拼接相结合的方法来构造最终的运动全景图，最终在全景图中保留运动对象不同时刻的多个形态.该方法的主要思想是：先根据光流法提取视频中的若干关键帧，然后以关键帧图像中的显著性区域作为约束对象分别实现基于内容的全景拼接图像，再结合图像分割算法将各张全景拼接图融合到一起，最终实现包含多运动对象的全景拼接图.运动全景图的拼接主要有两个步骤：1) 关键帧的提取与图像序列对齐；2) 运动全景图的融合.

1.4.1关键帧的提取与图像序列对齐

由于处理的对象是摄像机平面运动状态下拍摄的存在局部运动的视频，方法的目的是要捕捉对象的全局性运动，所以可以利用基于运动分析的方法[12]提取关键帧.首先，快速提取光流信息[8]；然后利用光流信息分析计算运动量，选取运动量达到局部最小值的点作为关键帧.各关键帧中的运动对象构成的运动轨迹大致涵盖了视频中的主要运动信息，本方法把关键帧中的运动对象定义为显著运动对象，拟对视频的显著运动对象进行检测与提取，然后把这些对象作为约束条件分别进行全景图拼接.

在确定参考帧后，需要对图像序列作对齐操作.本方法实现时选择无约束条件的拼接图作为参考帧，然后对其他带约束条件的全景图作对齐变换，把它们全部对齐到参考帧坐标系中.待变换的图像需要与参考帧图像找到对应关系，才能进行对齐变换.两者之间的对应关系可以用单应矩阵来表示.求解单应矩阵的过程如下：1) 检测图像的局部特征；2) 为每个特征提取特征描述符；3) 根据特征描述符进行特征点匹配；4) 利用RANSAC方法求出单应矩阵.

接下来，对每帧图像进行Harris特征提取，把待对齐的图像与参考帧图像的特征点进行匹配，建立对应关系，可用公式表示为

ui=Hijuj

(9)

其中：Hij记为单应矩阵；ui和uj分别为特征点在图像中的具体位置(x,y坐标).

最后，根据单应矩阵对图像进行仿射变换，把其他带约束条件的全景图像对齐到参考帧坐标系中.

1.4.2运动全景图的融合

在根据Harris角点特征匹配的基础上对齐各张全景图像后，可直接进行运动全景图的融合，得到包含多个运动信息的全景图.但是，直接融合的图像中运动对象明暗不一，部分图像细节丢失，显著对象信息不突出[13].所以，为了解决上述问题，我们采用图像抠像技术预先对带约束的全景图像实现前景运动对象的提取，得到相应的前景控制图(mask图)，再进一步实现图像融合.

首先，对带约束的全景图像作处理以实现全景图像的前/背景分割[14].该方法利用简单的人机交互，用户只需在前景对象以及背景对象上各取几个点作为样本输入，就可以实现理想的前/背景分割.此外，引入非局部区域的k近邻区域来代替原有的局部线性窗口区域，不需要建立局部的线性色彩模型，也不要进行复杂的抽样策略，大大提高了算法的实现效率.与此同时，该方法对于前景对象的细节处理也非常到位，能够提取出较为细致的前景对象.

然后，结合预生成的mask图，利用加权平均算法来实现图像融合.不同全景图运动对象有可能出现重叠的现象，其权重的大小根据时间的先后原则来确定.假定无约束条件的全景图像的像素值记为pm(i,j)，其他各张带约束条件的全景图像的像素值记为pi(i,j).两张图像的融合方法为

(10)

其中pn(i,j)为新生成的图像.如果时间上较早发生的运动形态，设置较大的权重值，然后根据时间顺序依次递减.本方法在实现时，设置α1=0.9，α2=0.8.

根据以上算法分别对mashu.avi和jieli.avi视频进行了运动全景图合成，结果如图6所示.在全景图中，我们采用连续的透明度表示运动的发生时间，透明度越大则表示发生时间越早，通过该形式就可以间接表现出对象的运动轨迹.

图6　运动全景图效果 Fig.6　Motion panorama stitching image

通过实验效果分析发现：该方法在一定程度上达到了用户想要在全景图中看到运动对象的运动信息的期望，但是，其实现速度还是相对较慢.因此，可以基于CUDA并行计算方法实现算法加速优化.

2基于CUDA的全景拼接图的加速与优化

视频全景拼接过程中，视频帧的分辨率以及帧数的多少是影响拼接速度的主要因素.基于流形的拼接算法主要包括邻接矩阵的构建和寻找最短路径，因此CUDA上的加速与优化也从这两部分展开.

2.1邻接矩阵的构建

邻接矩阵的构建主要包含邻接结点的确定和权重的设定，相邻两个结点所在像素列之间的颜色差值决定了连接边的权重值D(V,V′).邻接矩阵的赋值需要遍历每个结点，然后计算每个结点与其邻接结点之间的权重值.结点数目越多，计算越慢.但该计算过程的逻辑是很简单的，而且每相邻两个结点之间的计算与其他结点之间也相互独立.因此，该过程可以通过GPU的多线程来对其优化.

假定视频大小为640×480×50，结点个数即为640×50.视频的邻接点在帧间的转变范围和像素列在相邻帧上的x范围分别为xrange=[1，2，…，10],trange=[0,1]，那么图像的邻接结点可取当前帧的下一像素列，以及下一帧图像对应位置的像素列到下10个像素列.为方便计算，把每个像素点定义成一个结构struct mpixel {intr; intg; intb;}，该结构中包含了像素点的rgb信息.

然后，开辟显存空间来存放计算结果.数组result用来存放每个线程的计算结果，定义其大小为640×480×50×11.用数组dis来存放每个结点与其11个邻接结点之间的距离，定义其大小为640×50×11.视频信息所需存储超过显存连续可开辟的最大空间时，可采用分块传输与计算.

大小为640×480×50的视频，可有640×50个结点并行计算权重.开辟640×50个block，每个block的工作是计算当前结点的邻接信息.再给每个block开辟480个线程，每个线程对应一个像素点.独立计算当前像素与其他11个相邻像素之间的颜色距离，该计算过程见图7.

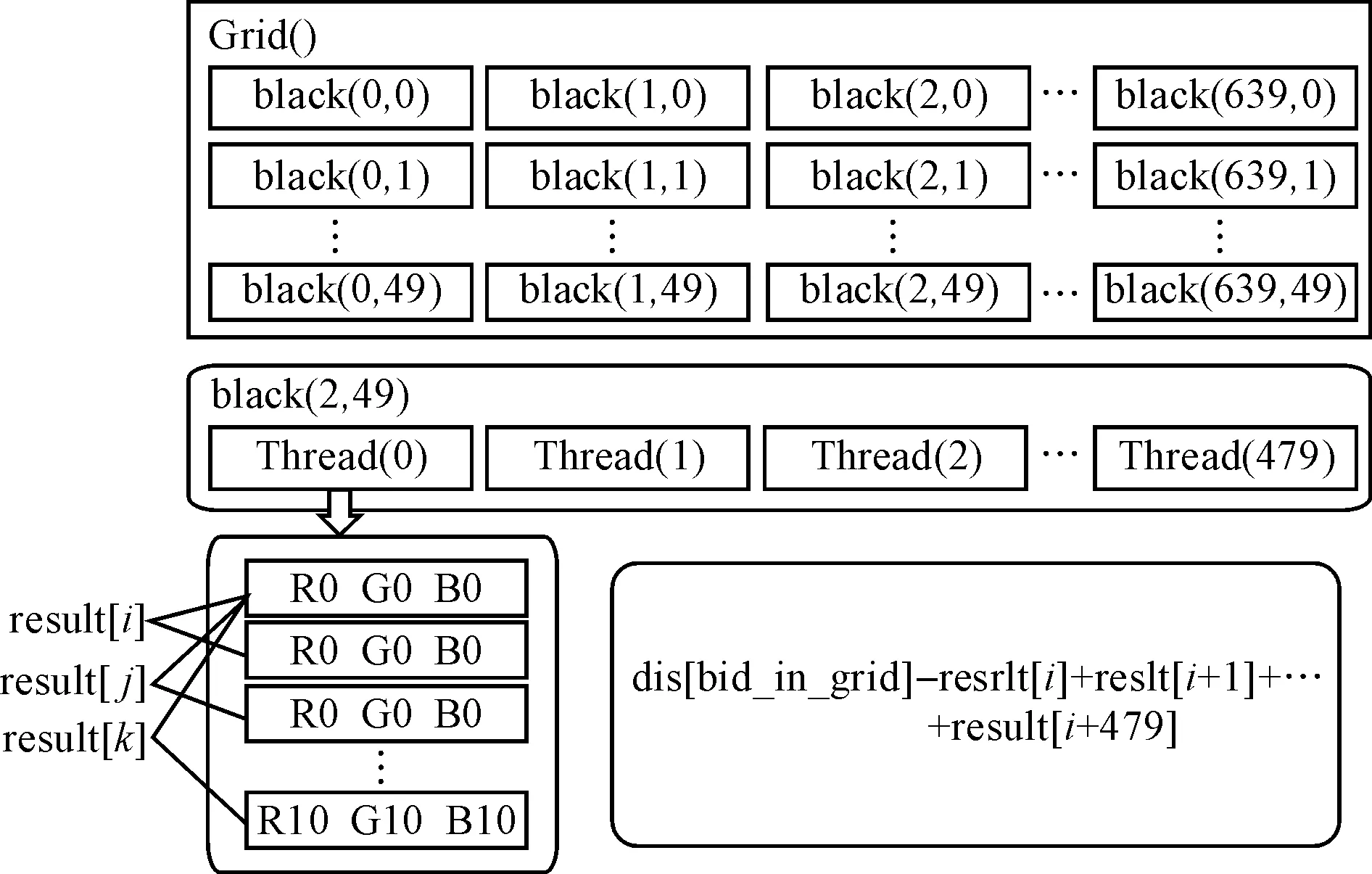
图7　CUDA的并行结构 Fig.7　Parallel structure of CUDA

根据内建函数变量blockIdx.x，blockIdx.y获取block在网格grid中的索引号bid_in_grid，变量threadIdx.x获取线程thread在网格中的索引号tid_in_grid.计算完每个结点的邻接信息之后，需要对block中的所有线程进行累加获取一整个像素列的颜色距离.可用公式表示为

(11)

每个线程都有11个邻接信息，每个邻接信息都要进行累加计算，该累加过程可让11个线程并行计算，每个线程进行累加计算时，可通过归约算法进一步提高计算效率.

2.2最短路径搜索算法的并行计算

影响拼接速度的另外一大关键就是最短路径的查找，Dijkstra算法的主要步骤Initial，ExtractMin和Relax都可以通过CUDA来加速实现，其具体的算法步骤如下：

在ExtractMin部分，可利用Reduction来加速，其算法复杂度为O(logn).在CUDAC平台中有一个模板库Trust，它封装实现了并行计算的函数接口，Reduction就是其中的并行计算方法.Reduction算法利用二分法来将一组数据转换成某个要求的数值，比如，可以利用该算法实现最小值的查找.

Relax部分的主要工作是判断是否需要更新最小值.若是d[u]+c(u,v)

若每个结点的邻接结点个数很少，该并行算法将不能体现并行的优势，反而会因线程的频繁调度反而会影响程序执行的效率.最短路径搜索的并行计算采用Δ-Stepping算法[15]实现，该算法是Dijkstra的最优改进算法.Δ-Stepping算法是一种基于桶并行Dijkstra算法，它用多个桶Buckets来保存结点，每个桶中保存的结点个数与Δ的大小密切相关.在桶B[i]中保存的结点为{v∈V且tent(v)∈[i×Δ,(i+1)×Δ}，V表示结点集合，tent(v)表示从源结点到结点v的累积权重值.其中Δ的取值有三种选择：权重中值、权重平均值、最大权重值除以节点出度最大值的商，这里采用第三种方法.

3实验结果分析

笔者在CPU为Intel(R)Core(TM)2DuoCPUE8300@2.83GHz2.83GHz、内存为2 048MB(DDR2SDRAM)、显卡为NVIDIAGeforceGTX580且安装MicrosoftWindows7操作系统的机器上实现了算法代码.此外，为了比较不同算法在处理效率上的差异，除了在VS2008平台上结合OPENCV开发库和CUDA开发库，实现了基于CUDA的并行优化方法，还在MATLAB平台上实现了基于流形的视频拼接方法和基于高斯金字塔结构的视频拼接串行优化方法.

对两段视频friend.avi和hanbing.avi分别采用CUDA加速下的带显著性区域约束的视频图像拼接方法、基于高斯金字塔结构的串行优化拼接方法和直接拼接方法进行实验，实验结果如图8，9所示.三种方法都可以通过保留某一帧图像中的显著性区域或者固定区域，生成带约束的全景图；但是，对于包含局部运动的视频，带显著性区域约束的视频图像拼接方法还可以生成运动全景图，在全景图中以时间顺序突显出对象的运动轨迹，如图8(c)和图9(c)所示.三种方法进行带约束的视频拼接时，在不同帧数情况下实现的时间如表1所示.

图8　friend.avi视频全景图拼接结果 Fig.8　Panorama stitching reults of friend.avi

实验结果表明：三种方法均可以生成带约束的视频全景拼接图，该全景图可以保留指定时刻的运动对象形态，在实际应用过程中，能够满足用户需求；而笔者提出的方法还可以生成运动全景图，该全景图保留了多个时刻的运动对象形态，有助于用户通过全景图获取视频中运动对象的形态变化情况，对于了解视频详细内容有更大的帮助.因此，提出的方法更适合实际应用.

图9　hanbing.avi视频全景图拼接结果 Fig.9　Panorama stitching results of hanbing.avi

视频名称视频大小带显著性区域约束的视频图像拼接/s定义邻接矩阵搜索最短路径总时间基于高斯金字塔结构的串行优化拼接/s第4层第3层第2层第1层总时间直接拼接总时间/sfriend.avi720×480×50720×480×100720×480×150720×480×2001.8563.7445.6007.6347.70318.15527.68736.8919.55921.89933.28744.52522342347812182227659314739821181802865828901165hanbing.avi640×360×50640×360×100640×360×150640×360×2001.2942.5893.8695.1466.22012.49119.07424.8937.51415.08022.94330.0391112123479101341556374506777932615367941055

虽然三种方法都可生成带约束的全景图，但是其拼接速度有很大的差异.基于高斯金字塔结构的串行优化拼接方法比直接拼接的方法在实现速度上有很大提高；而采用CUDA并行加速的带显著性区域约束的视频图像拼接方法在处理时间上明显快于其余两种方法；因此，我们提出的带显著性区域约束的视频图像拼接方法在采用CUDA并行计算方法后，有明显的加速效果，可以应用于分辨率更高、时间更长的视频，进一步扩展了方法的适用性.

4结论

笔者从视频内容出发，提出了一种带显著性区域约束的高效视频图像拼接方法.采用基于时空空间的流形拼接算法，把视频拼接问题划归为图论问题，满足了用户希望保留某一帧图像中的显著性区域或者固定区域的需求.同时对于包含局部运动的视频，先通过基于光流场的方法实现关键帧的提取，然后对关键帧中的显著对象进行提取并作为约束对象分别实现带约束的全景拼接图.最后，提出了基于CUDA并行的优化方法，改善了在处理时间较长、分辨率较高的视频时拼接速度较慢的问题.实验结果表明基于显著性约束的视频图像拼接方法生成的运动视频全景图像拼接结果能够满足实际应用需求，产生的多运动形态全景图能够帮助用户更好地理解运动视频全貌，而CUDA加速方法的应用进一步提高了拼接速度，使图像拼接技术可以适用于更高清、时间更长的视频.

参考文献：

[1]郑莉莉,黄鲜萍,梁荣华.基于支持向量机的人体姿态识别[J].浙江工业大学学报,2012,40(6):670-675.

[2]PELEG S, HERMAN J. Panoramic mosaics by manifold projection[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Juan: IEEE,1997:338-343.

[3]ZOMET A, PELEG S. Efficient super-resolution and applications to mosaics[C]//International Conference on Pattern Recognition. Barcelona: IEEE,2000:579-583.

[4]PELEG S, ROUSSO B, RAV-ACHA A, et al. Mosaicing on adaptive manifolds[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(10):1144-1154.

[5]RAV-ACHA A, SHOR Y, PELEG S. Mosaicing with parallax using time warping[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops. New York: IEEE,2004:164-164.

[6]WEXLER Y, SIMAKOV D. Space-time scene manifolds[C]//10th IEEE International Conference on Computer Vision (ICCV 2005). Beijing: IEEE,2005:858-863.

[7]张树江,邢慧,颜景龙，等.一种改进型视频全景图流形绘制方法[J].光子学报,2007,36(s1):299-302.

[8]HU F, LI T, GENG Z. Constraints-based graph embedding optimal surveillance-video mosaicing[C]//Asian Conference on Pattern Recognition. Beijing: IEEE,2011:311-315.

[9]郭李云,欧阳宁,莫建文.长视频序列拼接[J].计算机工程与应用,2011,47(14):183-185+195.

[10]张美玉,简睁峰,侯向辉，等.Dijkstra算法在多约束农产品配送最优路径中的研究应用[J].浙江工业大学学报,2012,40(3):321-325.

[11]彭宏,韩露莎,王辉，等.基于小波变换与多帧平均法融合的背景提取[J].浙江工业大学学报,2013,41(2):228-231.

[12]LIU C. Beyond pixels: exploring new representations and applications for motion analysis[D]. Boston: Massachusetts Institute of Technology,2009.

[13]TANG C K, LI D, CHEN Q. KNN matting[C]//IEEE Conference on Computer Vision and Pattern Recognition. Providence: IEEE,2012:869-876.

[14]WOLF W. Key frame selection by motion analysis[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. Atlanta: IEEE,1996:1228-1231.

[15]MEYER U, SANDERS P. Δ-stepping: a parallelizable shortest path algorithm[J]. Journal of Algorithms,2003,49(1):114-152.

(责任编辑：刘岩)