改进粒子群搜索的二维皮革排样优化算法
2016-01-22陈志杨,刘妍
改进粒子群搜索的二维皮革排样优化算法
陈志杨,刘妍
(浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
摘要:针对传统的排样方法普遍利用率不高且母版多为矩形的问题,提出了一种在不规则皮革母版上提高排样利用率的方法,在排样策略与组合优化上同时进行改进,减少母版的浪费区域.在皮革样片分块排放原则的基础上利用最优匹配原则将不同级别的待排样片排入质量分级区域,然后结合改进粒子群搜索算法来优化预排样中原始样片排布不够紧凑的问题,实现皮革的优化排样.实验结果表明:所提方法在满足工艺要求的基础上可以提高皮革的利用率,得到较好的排样效果.
关键词:分块排样;最优匹配;改进粒子群搜索
收稿日期:2015-03-05
基金项目:国家自然科学基金资助项目(61303138)
作者简介:陈志杨(1971—),男,河北秦皇岛人,教授,研究方向为计算机辅助设计(CAD)、几何造型和图形处理,E-mail:czy@zjut.edu.cn.
中图分类号:TP391
文献标志码:A
文章编号:1006-4303(2015)05-0492-05
Abstract:Focusing on the the problem of low utilization and restricted rectangle shape in the traditional nesting way, a method that can improve the utilization of irregular-shape sheets is proposed in this paper. The method improves nesting strategies and combinatorial optimization so that can reduce the waste region on the master. The best-matching rules are used to pack the different levels samples to quality staging area. Then the modified particle swarm optimization search algorithm is used to deal with the problem that the original sample arrangement is not compact enough. It will optimize the leather nesting algorithm. The result show that this method not only meet the technological requirements, but also improve utilization and get the good nesting result.
Keywords:partition nesting; best-matching; improved PSO search
Optimization algorithm of two-dimensional leather nesting
based on improved PSO search
CHEN Zhiyang, LIU Yan
(College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China)
工业生产中,排样问题有着广泛的应用,如在服装制造业,木材、皮革等领域的下料问题[1].在皮革加过程中,皮革的裁剪工艺直接影响到皮革制品的优劣,因此对皮革加工质量,效率的要求也越来越高[2].因为皮革材料边缘不规则,质量分布不均匀,母版的重复加工率低,所以提高皮革排样的利用率是一个重要问题[3].对于二维排样问题,不少学者进行过研究.矩形件排样按照排入策略可分为BL算法[4-5]、改进BL算法[6-7]、填充算法[8]等,按组合优化算法可分为遗传算法[9]、蚁群算法[10]、粒子群算法[11]等.曹炬[12]提出的背包算法可以快速找到近似最优解,但是计算复杂度较高.黄少丽等[13]提出了组块策略.刘瑞杰等[14]使用蚁群算法来求解矩形件优化排料问题,将排样问题用树来描述,将问题转变成求取面积最大的二叉树.梁利东等[15]提出矩形动态匹配算法,能较好的解决矩形板材的排样问题.目前,针对矩形件的排样问题主要是将定位求解与定序求解相结合来获得最优解.
本算法的研究目标是实现皮革母版上的分块排样,提高利用率.之前的许多排样办法都是在规则的矩形母版上排样,这种方法不适合皮革不规则的轮廓,同时没有考虑到工艺要求.通过在皮革母版上进行质量分块,采用不同的排样规则,满足分割要求,同时各部分分别采用粒子群改进算法,丰富了粒子种群的多样性.在最优匹配原则排样情况下,使用改进的粒子群算法能更好的寻找样片的排样位置,使各个样片更紧凑的排布在一起,提高排样的利用率.
1排样要求与问题描述
1.1排样要求
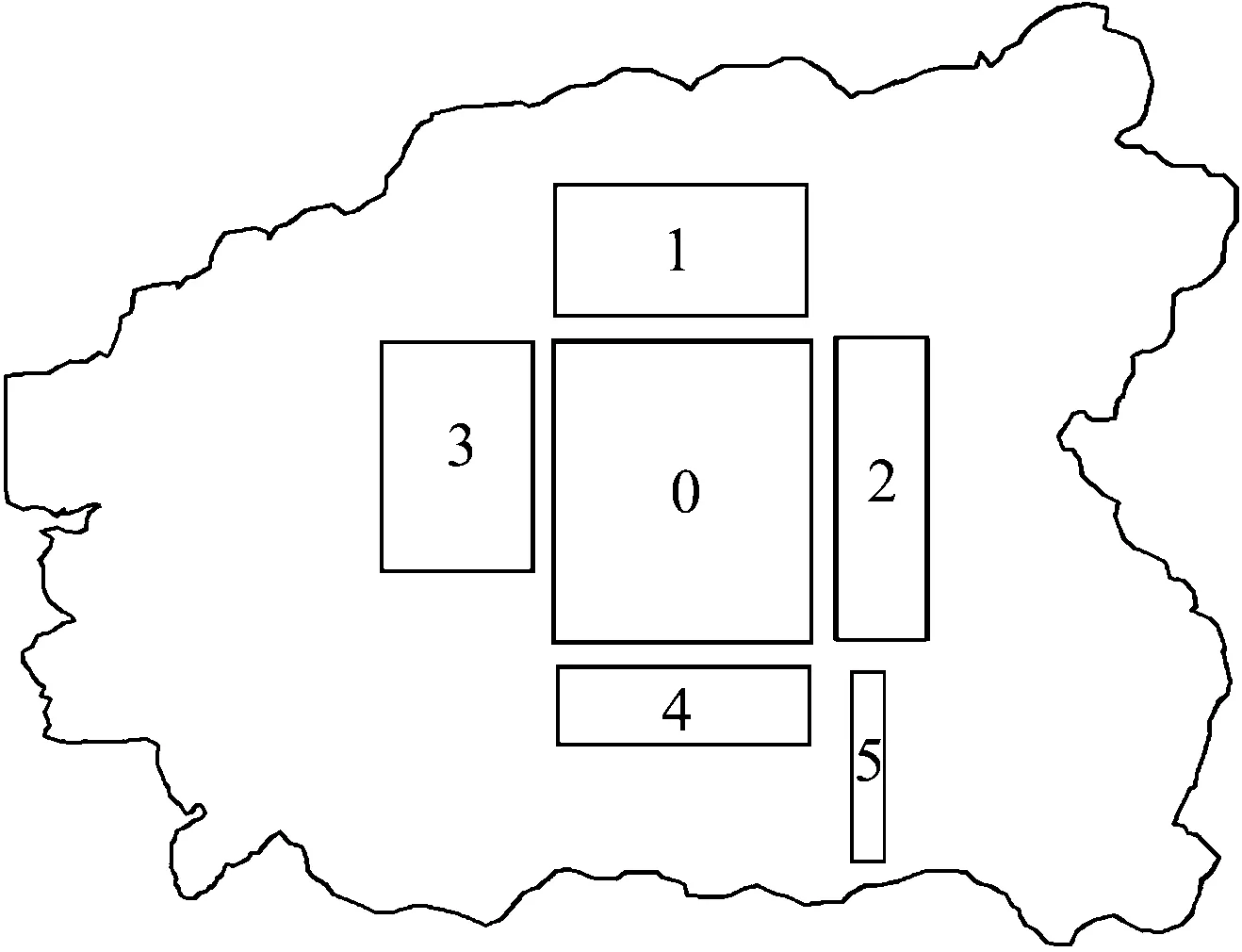
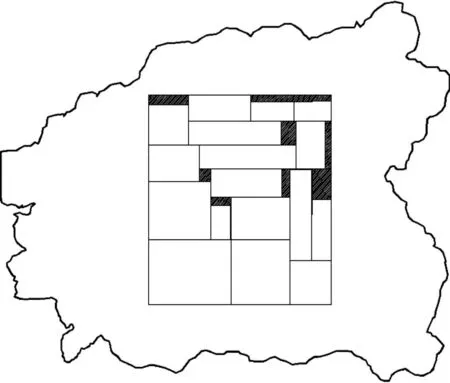
在皮革加工行业,因为皮革材料的特殊性以及生产工艺的要求,常常需要在不规则母版上划分出质量优劣区域,同时将待排样片划定级别.在质量较好,瑕疵较少的区域排放一级样片,瑕疵较多的区域排放二级样片.一级母版划定为一个宽为W,高为L的矩形区域,其中排放N个矩形样片R;每个矩形样片R的高和宽为hi,wi;二级母版是不规则母版除去一级母版之外的区域.皮革排样的约束条件是将一级样片放置在一级母版上,二级样片放置在二级母版上,Ri,Rj(0 1.2排样问题描述 初始排样采用最优匹配算法.最优匹配算法是一种边长匹配算法,利用边长与待排母版的剩余长度相似度进行选择排样,使母版的利用率达到最大.该算法是先将一级样片与二级样片分别按宽度大小进行排序,宽度大的排在存储数组的前面,相同宽度的样片按高度递减的顺序依次存储,然后选择其中面积最大的开始排样,先排放面积大的样片,再排放面积小的样片. 优化排样算法的方法是首先按最优匹配原则将所有的原始样片排入指定区域,求出此时的母版利用率,然后用改进粒子群算法搜索每个样片的最优排放位置,横放或者竖放,更新粒子群的粒子值,按最优匹配将样片排入.如果经过粒子群搜索之后,求得最大的母版利用率,则此时粒子代表的各个样片排放位置认定为最优排样方案.如果搜索算法求得的利用率小于第一次的母版利用率,则认定初始排样位置是最优方案. 2算法描述 为了提高皮革的排样利用率,在满足工艺要求的基础上,采用分块排样与最优匹配相结合的方法对待排样片进行预排样,求得预排样的利用率.在此基础上,用改进的粒子群算法搜索原始样片是否有更合适的位置放置,从而使排样的效果更加紧凑. 2.1一级母版放置 一级母版区域的排放步骤为:1) 将一级母版最下面的边设置为初始最高轮廓线,一级母版的宽设置为初始剩余宽度,记录此时的最大高度为零;2) 当按面积大小依次排入零件Ri时,在最高轮廓线选择最低的一段,如果同时存在几段,选择最左边的一段,测试该段的宽度是否大于或者等于Ri的宽度. 如果Ri宽度小于该线段宽度,将样片排入;如果Ri宽度大于该线段宽度,从剩余样片中选择样片宽度最接近剩余宽度的样片排入.排入后更新剩余宽度,判断此时的高度是否大于原来最高轮廓线的高度.如果超过,则更新此时最大的高度为最高轮廓线,即Ri所处位置的高度.重复步骤2,直到所有样片都排入一级区域. 如图1所示,4个矩形按面积大小排列.当1,2确定位置后,一级母版剩余的宽度不能放置第3块矩形,则从剩余的矩形中选择宽度小于或等于剩余宽度的矩形放置.1,2,4放置好之后,此时最高轮廓线为2的高度,则将第3块矩形放在第2块矩形的上面,同时更新最高轮廓线的高度. 图1 一级边长匹配过程 Fig.1 The matching process of the first-level side length 如果第一块一级母版排完规定的一级样片后还有剩余,即最大高度小于划定的高度L,可将第二块中一级样片放置在第一块一级母版中,提高板材的利用率. 2.2二级母版放置 二级区域是不规则母版除去一级区域外的不规则图形,一级区域一般位于母版中间位置,因此二级样片是向中间一级母版靠拢.二级样片放置采用边长匹配融合原则. 首先将一级母版区域定为原始融合图形,原融合图形的边长分为竖直于水平线与平行于水平线两种,称为竖界边与横界边,分别将原融合图形横界边与待排样片的宽度进行相似性匹配.相似度由两边的长度比例表示,越接近1,表明相似度越好.找到相似度最高的样片之后,同时比较竖界边与待排样片的高度是否相似度更好.如果相似度更好,则将该待排样片定位在原融合样片横界边的位置.选定在各个边长上定位的待排样片后,与母版边界进行检测碰撞.如果没有重叠,则将这些待排样片与原融合图形进行融合,删除重复的点,形成一个新的融合图形进行下一轮的排样筛选. 依次比较原始融合图形与该二级样片的各个边长,设定s为两个宽度之比,t为两个高度之比,v为标记位.s,t,v各位的取值如表1所示.标志位v=0,表示样片进入下一次筛选;v=1时,表示样片可放置在原融合样片的竖界边位置上;v=2时,表示样片可放置在原融合样片的横界边位置上;v=3时,表示样片有两个位置可以选择,在竖界边和横界边上都能进行定位. 表1 母版与样片边长比例情况 原始融合图形中横界边和竖界边的个数分别为n1,n2,每次定位选择n1个标志位为2和n2个标志位为1的二级样片分别放置在原始融合图形的各个边上,将这些二级样片与原始融合图形进行融合,把重合的点去掉,形成一个新的融合图形.融合过程就是将新加入进来的点集重新排序,同时删除多余的点.标志位为3的图形可以替代任一标志位为1和2的样片.这个过程不断重复,直到所有的样片都放置完毕. 图2中矩形0为一级母版,1,2,3,4,5分别为按面积排序的5个矩形样片,依次与一级母版的各个边长比较相似度.按照相似度由低到高将样片定位在图3中的各个位置,图4为融合之后形成的新融合图形. 图2 样片与融合图形 Fig.2 The samples and the fused images 图3 最优匹配定位 Fig.3 The best-matching location 图4 融合成新的融合图形 Fig.4 The new fused images 2.3基于改进离散粒子群算法的优化 单纯使用最优匹配方法排样会导致某些样片宽高比过大,排样结果不紧凑导致利用率降低.利用粒子群算法可全局搜索排样位置的最优解,在最优匹配的基础上对排样的结果进行优化.之前的研究大多使用标准粒子群算法进行优化,但是标准粒子群算法在求解非线性问题上容易陷入局部最优解[16-17],因此采用改进的粒子群算法对排样结果进行优化,更适合求解排样这种离散问题. 2.3.1标准粒子群算法 粒子群优化算法PSO(Particle swarm optimization)是在1995年由Kennedy等[18]提出,特征是简单,易操作,具有全局搜索能力.基本粒子群算法的数学描述是:粒子群优化算法中粒子的位置维度代表了该问题的一组解[19].粒子群算法初始为一群随机粒子,通过不断迭代找到最优解[20].每次迭代中,粒子按照一定的速度与位置的变化公式更新粒子位置以便搜索新解.用N维向量Xi来表示粒子的位置,Vi表示粒子的速度.假设个体极值Pbi代表当前粒子Pi的最优值,全局极值gbi表示整个种群目前找到的最优解. vin(m+1)=wvin(m)+c1r1[Pbin(m)-xin(m)]+ c2r2[gbin(m)-xin(m)] (1) xin(m+1)=xin(m)+vin(m+1) (2) 公式中第i个样片的排样方法为Xi= 2.3.2惯性权重分析与优化 许多研究表明惯性权值w对优化粒子群性能有着重大影响[21-23],w较小时有利于算法的局部搜索,w较大时在全局的搜索能力较强.在之前的研究中,大多数粒子群算法将w定义为一个小于1的常量.这样的结果是粒子的速度会越来越小,容易陷入局部最优解.针对这个问题,笔者所提方法采用改进惯性权重w的算法,使w随着迭代次数不断变化,在速度更新过程中快速找到最优解,从而改进了算法的性能.所提方法中w定义为 (3) 其中:N为总迭代次数;n为当前的迭代次数.采用这种定义的点是最开始的时候保持w为最大,在开始搜索的时候加快收敛速度.随着迭代次数的增加,w逐渐减小,可以防止错过最优解.在速度更新的过程中,自适应地改变惯性权重w,使粒子的收敛速度和收敛精度达到平衡状态. 2.3.3惯性权重分析与优化 矩形样片有横放,竖放两种放置方法,因此X的取值定义为1,0来表示当前样片为横放还是竖放.例如(000110000)表示将第4、第5个样片竖放,交换第4、第5个样片的宽和高进行排样,这样可以解决样片如果高度远大于宽度时,则在排样过程中会提高最高轮廓线的高度,导致利用率下降的问题.在优化算法中,第i个样片的X取值为1还是0采用随机生成的方法,在(0~1)中随机生成数字,同时设定中间值,小于中间值的保存为0,大于等于中间值的保存为1.经过多次测试,笔者认为中间值选择0.4可以得到较好的结果. 2.3.4两种粒子的适应度函数 一级母版区域是已知宽度W的矩形,全部排入一级样片时的最小高度Lm,第i个一级样片的面积为ai,定义适应度函数为 (4) 二级区域采用对最后的融合图形求取凸包面积aG.凸包面积包含了其中的一级母版的面积,假定一级母版的利用率为100%,即剔除一级母版后,求M2个二级样片的面积与凸包面积的比值.所以二级母版上的适应度函数为 (5) 两种适应度函数数值越接近1,解的质量越好.对不同区域采用不同的适应度函数来选择最优解,增加了粒子的位置多样性,更适用于分块排样. 2.3.5粒子群优化算法步骤 Step 1初始化粒子群,在(vmin,vmax)中随机生成每个粒子的速度,设定最大迭代次数N,随机生成粒子的位置,学习因子c1,c2,确定适应度函数F. Step 2计算每个粒子的适应度,将所有粒子中适应度数值最大的赋值给gb,对应将粒子Pi的适应度值赋值给Pbi. Step 3开始迭代计算.按式(1)更新粒子的速度,并限制在(vmin,vmax)中,按式(2)更新粒子当前的位置,更新粒子i的当前最优值Pbi以及全局最优值gb. Step 4若达到最大迭代次数,则结束;否则转Step 3. 3实验结果与分析 笔者在VC++环境下实现了不规则皮革母版的分区排样,表2中是排样的数据结果,母版的整体排样效果图如图5~7所示.图5中间区域为一级母版的初始排样情况,无色方块代表一级样片的排放位置,黑色方块为一级母版上的剩余面积.一级母版在初始排样后经过粒子群搜索优化,得到一级区域的排样优化图,如图6所示.图7为二级区域的优化排样结果,黑色阴影位置是图6中优化排样后的一级区域,虚线代表整体区域的凸包形状. 图5 一级区域初始排样图 Fig.5 The original layout of the first-level area 图6 一级区域优化排样图 Fig.6 The optimized layout of the first-level are a 图7 二级区域优化排样图 Fig.7 The optimized layout of the second-level area 由表2数据结果表明:经过优化算法之后,各级母版的利用率都得到了提高.根据初始排样图与优化图的比较,初始排样时各个样片按照边长匹配原则在各个区域中进行放置,母版的浪费区域较多,原因是有些初始样片的长宽比过大,按原始样片排放会产生最高轮廓线升高或者放置不下的问题,各个样片之间不够紧凑.经过粒子群优化算法得到适应度函数值最大的一组结果,使各个样片找到最优的排放方式,然后再按照边长匹配原则将各个处理后的样片排入,可以得到较优的排样结果. 4结论 通过分块排样,最优匹配原则,结合改进粒子群搜索算法,实现了皮革母版排样问题的优化,改进后的粒子群算法对惯性权重进行自适应设置,扩展了粒子种群的范围,一定程度上避免了算法“早熟”,从而在搜索最优位置上比基本的粒子群算法有更大的优势.此方法在满足工艺要求的同时,相比单纯使用最优匹配原则的排样办法增加了样片在母版上排样的聚合程度,提高了母版的排样利用率. 参考文献: [1]张玉萍,张春丽,蒋寿伟.皮料优化排样的有效算法[J].软件学报,2005,16(2):319-323. [2]易秋菊,曾睿,余洋,等.中国皮革行业面临的严峻形势和机遇[J].西部皮革,2009,31(5):13-17. [3]林智慧,史伟民,杨亮亮.电脑皮革切割机控制系统的研究[J].机电工程,2012,29(8):937-940. [4]BAKER B S, COFFMAN E G, RIVEST R L. Orthogonal packings in two dimensions[J]. SIAM Journal on Computing,1980,9(4):846-855. [5]CHAZELLE B. The bottom-left bin-packing heuristic:an efficient implementation[J]. IEEE Transactions on Computers,1983,32(8):697-707. [6]刘德全,滕弘飞.矩形件排样问题的遗传算法求解[J].小型微型计算机系统,1988,19(12):20-25. [7]董德威,颜云辉,王展.存在表面缺陷原材料的矩形件优化排样问题研究[J].东北大学学报,2012,9(9):661-664. [8]陶献伟,王华昌,李志刚.基于填充算法的矩形件排样优化求解[J].中国机械工程,2003,14(13):1104-1107. [9]张玉萍,宋健,蒋寿伟.基于离散化和遗传算法的皮革制造中的排样问题[J].计算机工程,2004,30(23):143-145. [10]刘瑞杰,王丽娟,史原.多种群蚁群算法在矩形件优化排料中的应用[J].江南大学学报:自然科学版,2013,12(13):287-291. [11]董辉,黄胜.二维排样中小生境粒子群算法的研究与应用[J].浙江工业大学学报,2014,42(3):257-268 [12]曹炬.二维异形切割件优化排样的拟合算法[J].中国机械工程,2000,11(4):438-441. [13]黄少丽,杨剑,侯桂玉,等.解决二维下料问题的顺序启发式算法[J].计算机工程与应用,2011,47(13):234-237. [14]刘瑞杰,须文波.求解矩形件优化排料蚁群算法[J].江南大学学报:自然科学版,2005,4(1):23-26. [15]梁利东,钟相强.基于矩形化动态匹配的船体零件排样算法研究[J].船舶工程,2013,35(1):68-71. [16]温涛,盛国华,郭权,等.基于改进粒子群算法的Web服务组合[J].计算机学报,2013,36(5):1031-1046. [17]盛煜翔,潘海天,夏陆兵,等.混合混沌粒子群算法在苯与甲苯闪蒸过程优化中的应用[J].浙江工业大学学报,2010,38(3):318-321. [18]KENNEDY J. Particle swarm optimization[J]. Proceedings of IEEE the International Conference on Neural Networks,1995(4):1942-1948. [19]黄太安,生佳根,徐红洋.一种改进的简化粒子群算法[J].计算机仿真,2013,30(2):327-330. [20]随聪慧,唐慧佳.改进公式的核心主子群粒子群算法[J].计算机应用,2011,31(5):1324-1327. [21]李欣然.粒子群优化算法研究[J].计算机与现代化,2010(6):6-8. [22]王延梁,王理,夏国平.基于混合粒子群算法的装运机械组合优化问题[J].系统工程理论与实践,2012,32(10):2262-2269. [23]韩冬梅,王丽萍,吴秋花.基于模糊偏好的多目标粒子群算法在库存控制中的应用[J].浙江工业大学学报,2012,40(3):348-351. (责任编辑:刘岩)