客观聚类分析对区域基础教育发展水平评价

客观聚类分析对区域基础教育发展水平评价

皮进修1， 刘晓静2

(1.重庆师范大学 数学学院，重庆 401331；2.重庆师范大学 图书馆，重庆 401331)

摘要：首先，以国内外建立的教育指标体系为指导，结合我国年度统计用指标，选取13个指标并建立综合评价指标体系；其次，借助因子分析法将评价指标综合为具有代表性的影响因子，算得全国区域综合得分；最后，通过客观聚类分析对区域基础教育发展水平进行综合评价.

关键词：基础教育；因子分析；客观聚类分析

doi:10.16055/j.issn.1672-058X.2015.0011.018

收稿日期：2015-03-31；修回日期：2015-05-11.

作者简介：皮进修(1989-)，男，湖南常德人，硕士研究生，从事经济系统分析研究.

中图分类号：O212文献标志码：A

基础教育的发展一直受到社会各界的关注，如何衡量全国各区域基础教育的发展水平就显得尤为重要.对全国各个区域的基础教育发展水平作出评价，是一个系统性的工作，影响因素来自社会各个方面，如果全部考虑进去，显然不符合实际.因此，首要任务就是考虑主要影响因素，确定评价我国基础教育发展水平的指标体系.已发现经济合作与发展组织(简称经合组织)、欧盟以及世界银行建立了系统性的教育评价指标体系[1].国内也有大量学者对教育指标体系进行理论研究，陈学军[2]介绍了经合组织教育指标体系概念框架及其内容的演变与发展；王燕[3]揭示了经合组织教育指标体系的理论框架指标研制的过程与方法.但很少有学者对某一阶段性的教育发展状况构建评价指标体系并且进行实证研究.此处以国内外建立的教育指标体系为指导，并结合我国年度统计用指标体系，确定从区域的人口因素、经济因素、教育经费投入、师资力量、政治因素等中选取13个指标，建立综合评价指标体系.通过因子分析将各个指标综合，得到了影响区域基础教育发展主因子，结合我国统计年鉴数据，算得各省市的综合得分，得到初步评价结果；基于因子得分将全国各区域进行客观聚类分析，对各区域基础教育发展现状行深入的评价和分析.

1区域基础教育发展水平评价模型的构建

1.1评价指标的选取

根据国际教育经济学的研究以及OECD，UNESCO，世界银行和欧盟教育指标体系研究，区域基础教育发展水平受到人口、经济、教育经费投入、师资力量、政治等众多因素的影响.根据影响因素作用的特点，可将其分为内生因素与外生因素[4].在分析参考国内外评价指标体系，结合影响因素的作用机理，外生因素选取了人口因素、宏观经济因素；内生因素选取了总教育经费、生均教育经费、发展规模、师资力量、基础能力设施构建评价指标体系，如表1所示.

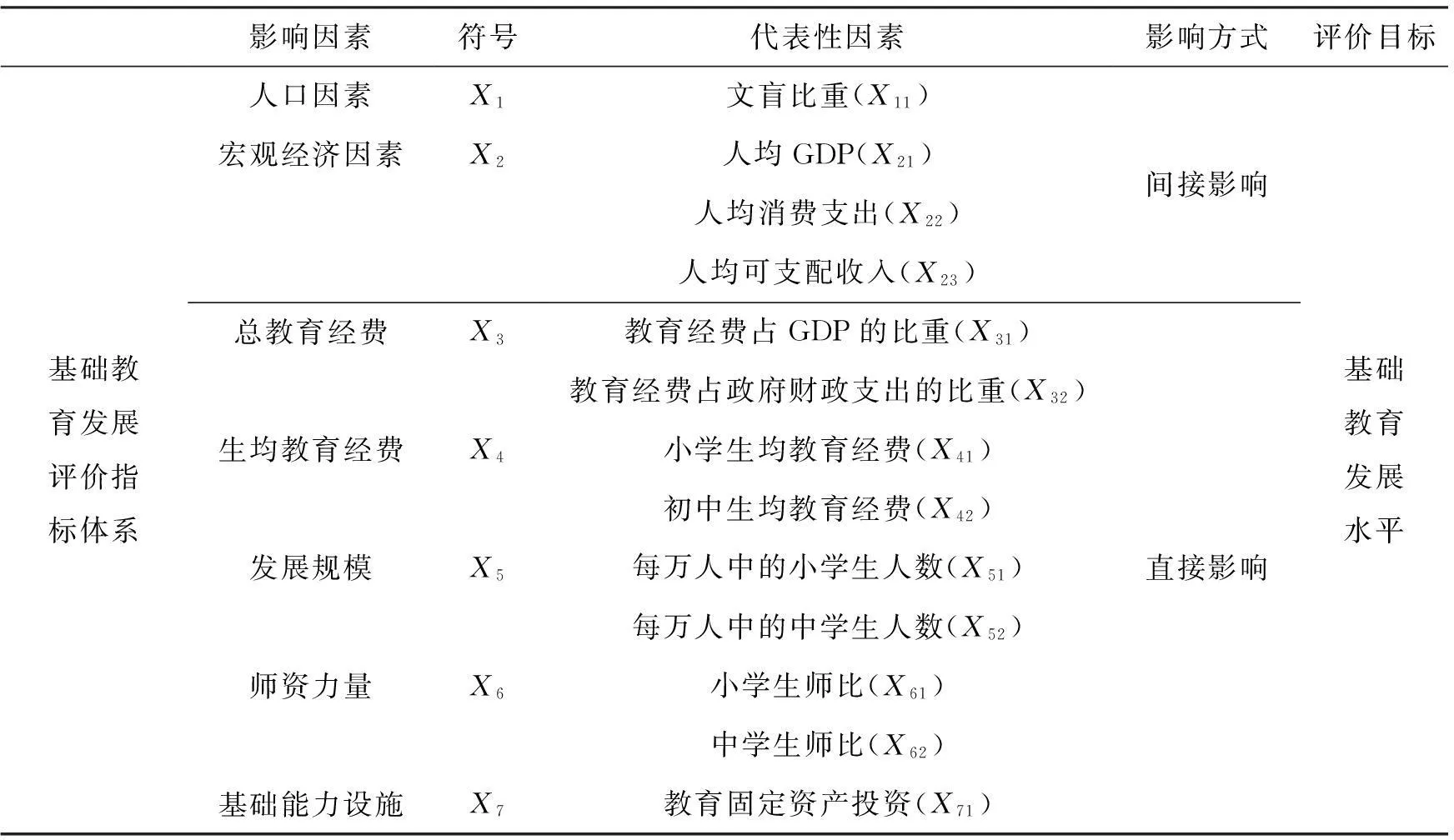
表1　评价指标体系及其作用机理

1.2数据来源

文中所涉及各项指标的具体数据均来源于《中国统计年鉴2013》《中国教育经费统计年鉴2013》中经网数据库以及2013年中国31省市的相关统计数据.

1.3因子分析及主成分选取

1.3.1因子相关性检验

因子分析的前提是变量间有较强的相关性.经计算结果KMO值为0.706>0.5，并且巴特利特球形检验，近似卡方值为552.023，显著水平值为0.000<0.005，达到显著性水平要求，表明相关系数矩阵与单位矩阵有显著差异，即原始变量间可能存在有意义的关系，因此可进一步做因子分析.

1.3.2因子分析过程和结果

运用统计软件SPSS19.0，对标准化的数据进行处理得到指标相关系数矩阵，并且求得相关系数矩阵的特征值、方差贡献率以及累积方差贡献率.利用主成分分析方法[5]，可以发现前3个因子的方差贡献率较大，累积方差贡献率达到85.574%>85%.因此根据主成分分析方法选取主成分的原则，选取前3个因子代表评价区域基础教育发展水平的13个指标的公共因子，是合适的.如表2是用SPSS19.0进行主成分分析,得到的主成分分析方差分解图.

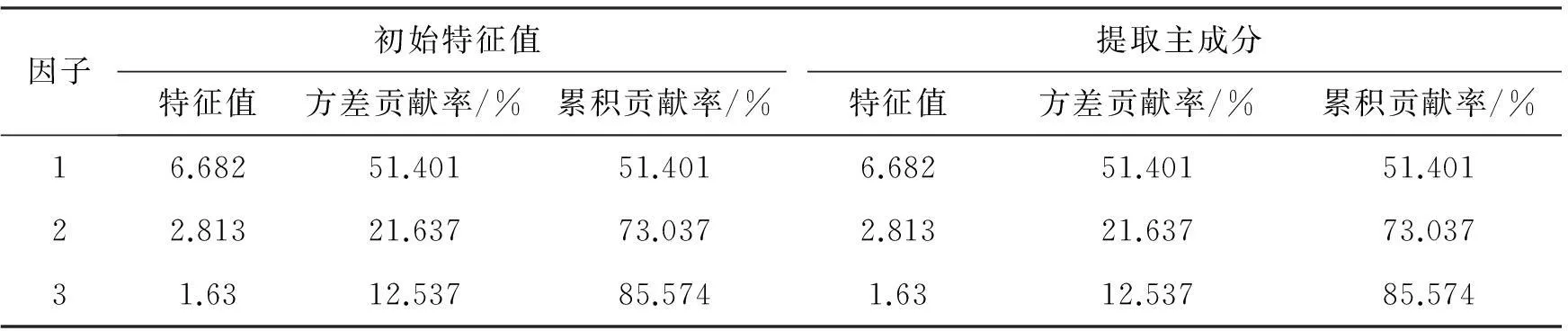
表2　主成分分析方差分解

为确定每个公共因子的意义以便作出科学合理的分析，可以对因子载荷阵实施一次旋转变换[6].旋转前，教育经费占GDP的比重(X31)、小学生师比(X61)同时在两个因子(因子1和因子2 )上的因子负荷超过了0.5，可以考虑进行因子旋转.利用Kaiser标准化正交旋转法，对因子载荷矩阵进行旋转得到旋转后的因子载荷矩阵如表3所示。

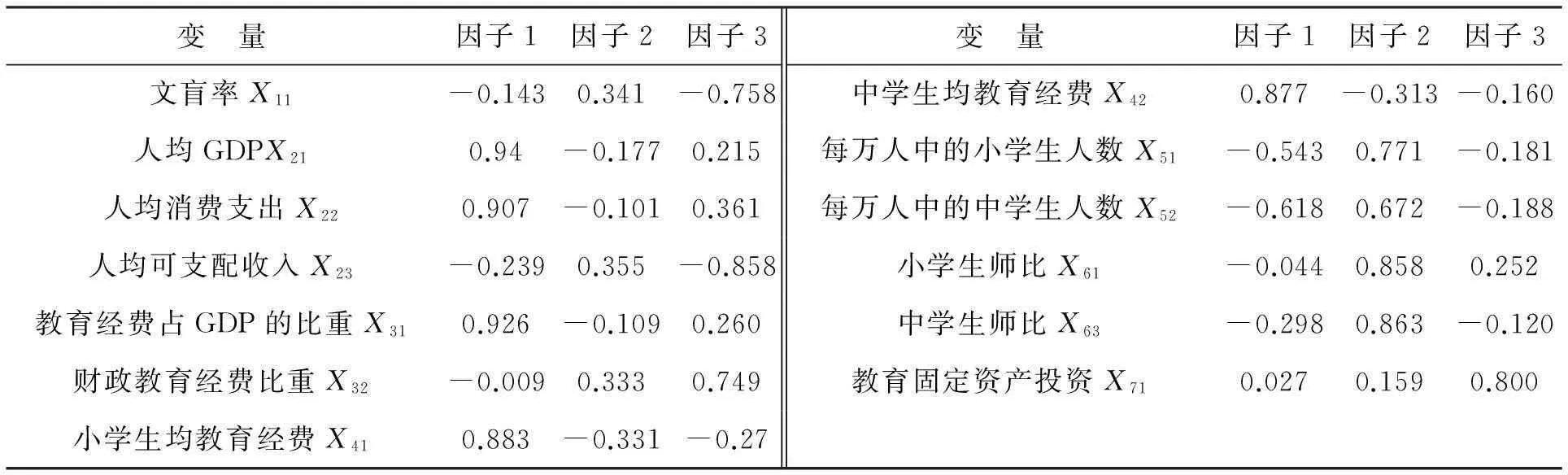
表3　旋转后因子载荷矩阵表

从表2、表3知，第一、二、三主成分对区域基础教育发展状况的解释贡献度分别为为51.401%，21.637%，12.537%，是所有主成分中最为重要的3个成分.第一主成分主要与人均GDP、人均消费支出、教育经费占GDP的比重、小学生均教育经费、中学生均教育经费等指标有较强的关系，不难发现，这些指标能从各个方面反映出区域经济实力状况，可以将它称为经济实力因子；第二主成分主要与每万人中的小学生人数、每万人中的中学生人数、小学生师比、中学生师比等指标有较强的关系，而这些因素能反映出各区域基础教育普及情况以及学校师资力量配备情况，因此可以间接得到基础教育在该地区的相对发展规模状况，称为生师比因子；第三主成分主要与人均可支配收入、财政教育经费比重、教育固定资产投资等指标有较强的关系，从这些指标来看，能够体现出各个区域对基础教育事业的投入状况，因此可称其为社会投入因子.

根据3个主因子的方差贡献度(作为权重)，旋转后因子载荷矩阵表以及各项指标极差标准化后的数据,利用主成分的计算公式可得各个区域基础教育发展状况的综合得分，其计算公式如下：

(1)

为了更加直观地了解各区域基础教育发展状况的综合得分，将式(1)的计算过程通过各区域基础教育主成分得分及综合得分排名表来反映(表4).

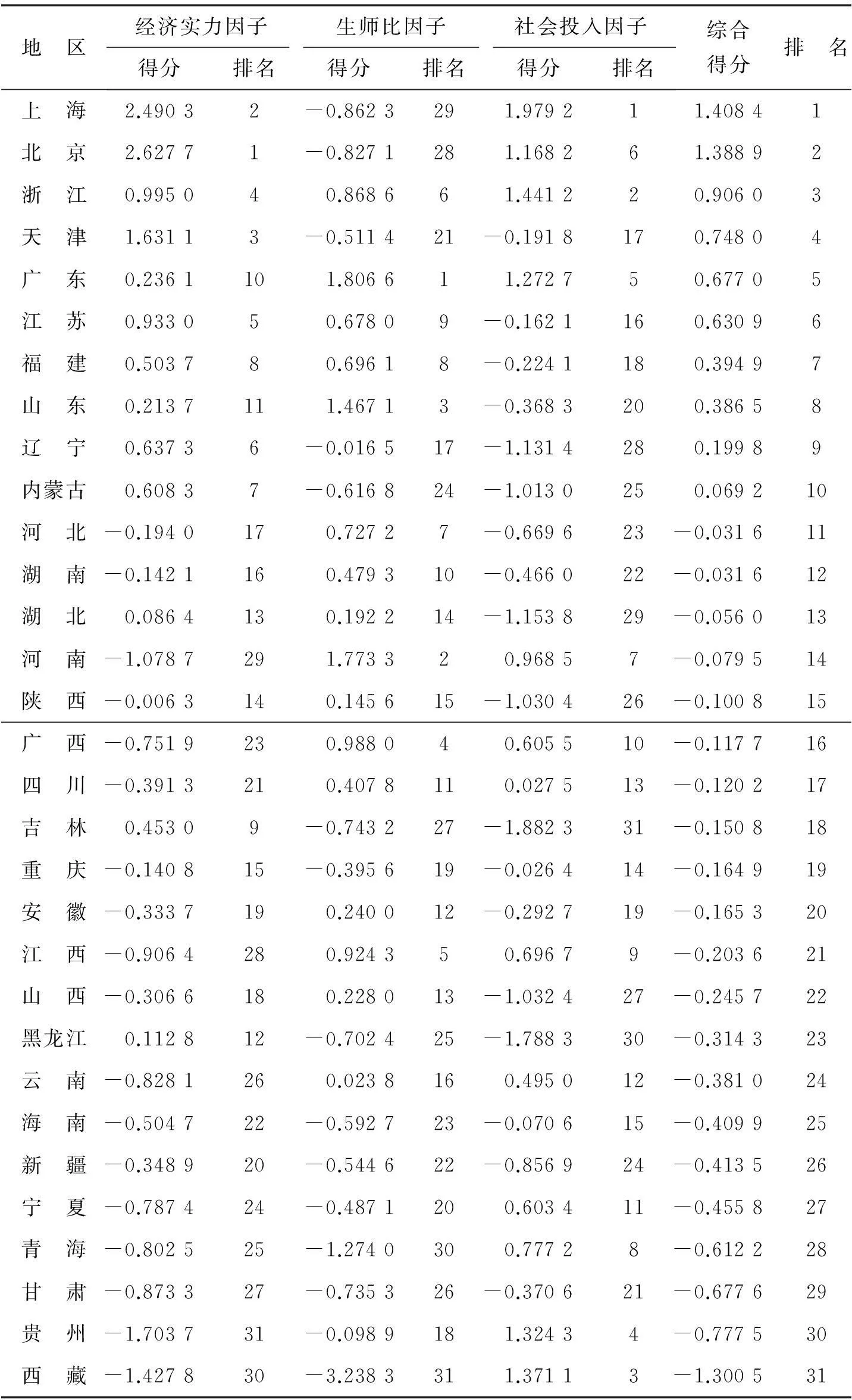
表4　区域基础教育主成分得分及综合得分

2客观聚类分析过程和结果

2.1客观聚类分析概念

Ivakhnenko院士将数据分组处理方法理论的原理与核心概念应用于聚类分析研究，从而得到一种新的聚类分析方法——客观聚类分析方法[7]，贺昌政、张九龙、林嫔[8]改进客观聚类分析法，使得新的客观聚类分析法能通过事先给定的一致性准则自动、客观地确定聚类个数并找到最优的聚类方案.客观聚类分析的基本思路：计算样本之间的距离，构建距离矩阵；利用偶极子将样本分组；在一致性准则下进行聚类分析.

2.2产生偶极子及子集A与B

将各区域的3个主成分得分作为客观聚类分析的3个指标集，并按综合得分排名对全国31个省市进行编号，比如编号1代表上海市，编号21代表江西.因为在计算综合得分时，各个因子得分的比重为其方差贡献度，因此，在计算样本间的距离时要对距离公式进行调整，并且因考虑了权重的影响，还需要对各个因子得分进行标准化再参与计算，于是得到调整后的距离如下:

(2)

其中，i=1,2,…，31；j=i,i+1,…，31；x*,y*表示标准化后的得分数据.

利用调整后的欧式空间距离公式以及表4中的数据计算得到各区域之间的距离并得到496个偶极子，将偶极子按其值从小到大排序，取前15个不重复的偶极子对，于是得到集合A，B如下所示：

偶极子：(29,28)，(22,11)，(23,16)，(24,13)，(10,9)，(25,12)，(18，15)，(2,1)，(19，17),(27,26)，(4,3)，(20，14)，(7,5)，(8，6)，(31,30).

样本子集A={29,22,23,24,10,25,18,2,19,27,4,20,7,8,31}.

样本子集B={28,11,16,13,9,12,15,1,17,26,3,14,5,6,30}.

2.3按子集A,B利用一致性准则αc聚类

通过计算，得到各种聚类方案的一致性准则αc的值，除了k=15,k=1的情况，k=4时，即为如下聚类方案时，αc的值为0,且在检验集C与D上聚类(除去k=15,k=1)，αc的值也为0，因此可以判断聚为4类时为最佳聚类方案，其聚类方案如表5所示.

表5　当 k=4时的聚类结果

3结论及建议

通过客观聚类分析，将全国各区域基础教育发展状况划分为4类，其结果及分析[9]如下：第一类：{上海，北京}；第二类：{福建，山东，天津，广东，辽宁，江苏，浙江，内蒙古}；第三类：{河北，湖南，河南，湖北，广西，陕西，四川，安徽，重庆，吉林，江西，山西，黑龙江，云南，海南}；第四类：{新疆，西藏，宁夏，青海，甘肃，贵州}.利用判别分析的方法，显然可以将江西省判到第三类中.第一类地区，基础教育发展水平在国内最好，但从生师比来看，存在教师资源利用不够合理的现象.第二类地区，主要出于沿海地区，地理优势突出，经济发展水平均衡，对基础教育的发展起到了支撑作用，生均教育经费较高，教育资源利用合理；第三类地区，主要分布在中国的中部以及东北部，因为地理条件的影响，经济发展相对落后于第一、二类地区，从社会投入因子得分来看，这一类地区的排名总体比较靠后，这说明这些区域对基础教育的投入力度还有待提高.第四类地区的经济实力因子得分排在末尾，是导致这6个区域基础教育发展水平排在最后一类的最主要的原因；因子排名基本上是最后几名，这体现出我国中西部省份的教育资源、师资力量是比较欠缺的，有待进一步的改善和提升.综合因子分析及客观聚类分析的结果，可见影响区域基础教育发展水平的重要因子是区域的经济实力、教育资源以及社会投入，尤其是政府主导的社会投入.因此促进区域基础教育发展，可以从3方面着手：

(1) 加大对基础教育资源的投入，尤其是教育经费占政府财政支出低于15%的地区，比如黑龙江、吉林、青海等省市的均未达到要求，鼓励社会捐赠以及适当放宽对教育事业筹措资金的要求.

(2) 优化对基础教育资源的配置效率，建立完善的基础教育绩效评价制度以及各项评价指标，并将绩效目标的各指标具体化，政府要及时收集绩效信息，调整资源导向以及预算安排.

(3) 提高师资力量水平，鼓励优秀教师到基层执教，缩小城乡师资水平的差距，完善教师资格定期审查制度，加大对在职教师定期培训力度.

参考文献：

[1] 张良才,孙继红.国内外教育指标体系分析与比较[J].教育学报,2009,12(6):60-68

[2] 陈学军.经合组织教育指标体系概念框架及其内容的演变与发展[J].比较教育研究，2006(8)：25-29

[3] 王燕.经合组织教育指标研制：理论过程与方法[J].比较教育研究,2012(2):80-84

[4] 杨大楷,王鹏.我国教育环境指标评价体系构建与测评[J].统计与决策,2014(12):27-30

[5] 岳斯玮.基于主成分聚类分析对区域教育综合发展水平评价[J].西南民族大学学报：自然科学版,2012(7):37-43

[6] 于秀林,任雪松.多元统计分析[M].北京:中国统计出版社,2011

[7] IVAKHNENKO A G,MUELLER J A．Parametric and Nonparametric Selection Procedures in Experimental Systems Analysis[J]．Systerns Analysis Modelling Simulation，1992，9(5)：157-175

[8] 贺昌政,张九龙,林嫔.基于数据分组处理方法的聚类分析模型[J].系统工程学报，2008,23(2):222-237

Research on the Development Level Evaluation of Regional Basic EducationBased on Objective Cluster Analysis

PI Jin-xiu1，LIU Xiao-jing2

(1.School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China;

2.Library, Chongqing Normal University,Chongqing 401331,China)

Abstract：The development of basic education has attracted the attention of social circles,and how to measure the development level of the regional basic education is particularly important. Firstly,on the guidance of education index system at home and abroad,this paper selects 13 indexes and establishes the comprehensive evaluation index system combining China's annual statistical index; secondly,the evaluation indexes are synthesized into representative impact factors by factor analysis,and the comprehensive scores of national region are calculated; finally,the development level of the regional basic education is evaluated comprehensively by cluster analysis,Through the objective cluster analysis for the comprehensive evaluation of the level of development of regional basic education.

Key words： basic education; factor analysis; objective cluster analysis