T-S模糊门在因果图中的应用

T-S模糊门在因果图中的应用*

严晓， 王洪春**

(重庆师范大学 数学学院，重庆 401331)

摘要：T-S模糊门在故障树分析中已得到广泛应用，并具有较好的实用性.鉴于因果图和故障树都可以用于故障诊断，用图形表示因果关系，两者具有很多相似性，并且在一定条件下，因果图和故障树可以相互转化，故将T-S模糊门引入到因果图中，考察其实用价值.

关键词：故障树；因果图；因果树；T-S模糊门

doi:10.16055/j.issn.1672-058X.2015.0011.009

收稿日期：2015-05-03；修回日期：2015-06-15.

基金项目：*国家社科基金(13BTJ008).

作者简介：严晓(1988-)，女，山东临沂人，硕士，从事人工智能研究.

通讯作者：**王洪春(1967-)，男，四川大竹人，教授，博士，从事人工智能、因果图、故障诊断研究.E-mail:wanghongchun@swsc.com.cn.

中图分类号：TP18文献标志码：A

故障诊断技术是一个模式识别问题，在传统的故障检测中，想要获得系统准确的概率是非常困难的，因此在故障树中引入了模糊数，模糊数是由美国计算机控制专家查德于1965年提出来的，用来解决不精确的模糊问题.因此将模糊数引入到故障分析[1]中，可以用来弥补故障树的不足.在传统的故障树分析中，故障树是由事件和门构成的，门用来描述事件之间的联系，事件可以用故障概率表示.在分析故障时，不仅要找到事物之间的联系，还要得到事件发生故障的精确概率，有一定的困难.为了解决系统之间的不确定性，文献[2]用模糊子集描述系统的失效可能性，模糊数用来描述故障状态，T-S模糊模型描述事件之间的联系，并验证了此算法的有效性.因果图和故障树都采用图形表示因果关系，并且两者有很多相似性，在一定条件下，因果图和故障树之间可以相互转化[3].此处所研究的因果图均为确定关系，没有耦合的故障树转化得到的因果图为因果树(此处所用的故障树是耦合的)[4]，故在T-S模糊门应用到故障树的基础上，将T-S模糊门引入到因果图中.

1T-S模糊门故障树的有关理论

T-S模糊模型构造逻辑门[5]，用来描述事件之间的联系，用T-S模型门取代原有的故障树逻辑门，形成了模糊门故障树[2]，如图1所示.其中用Y表示T-S顶事件，三角形表示T-S模糊门，xi表示基本事件(i=1，2，3).

1.1事件描述

图1　T-S模糊故障树

图2　隶属函数

1.2T-S模糊门

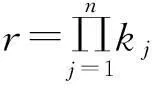
(1)

故上级事件发生的概率模糊性为

(2)

底事件记为X=(x1，x2，…，xn)，它出现故障的状态记为X′=(x1′，x2′，…，xn′).则通过计算，可以估算得到上级事件发生故障的模糊概率：

(3)

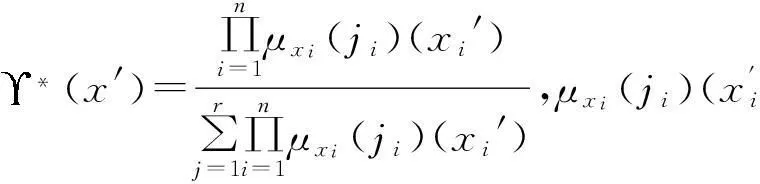
2实例分析

在进行因果图分析时，选取确定的因果关系，类比于故障树，因果图中的中间事件相当于故障树中的顶事件和中间事件，因果图的基本事件相当于故障树的底事件.在因果图中，因果图中的每一个节点事件相应对应一棵微因果树，应此可以将因果图分成若干个小的模块，通过对小模块进行整合得到因果树，在因果树中运用模糊门.图3是某系统故障的因果图.

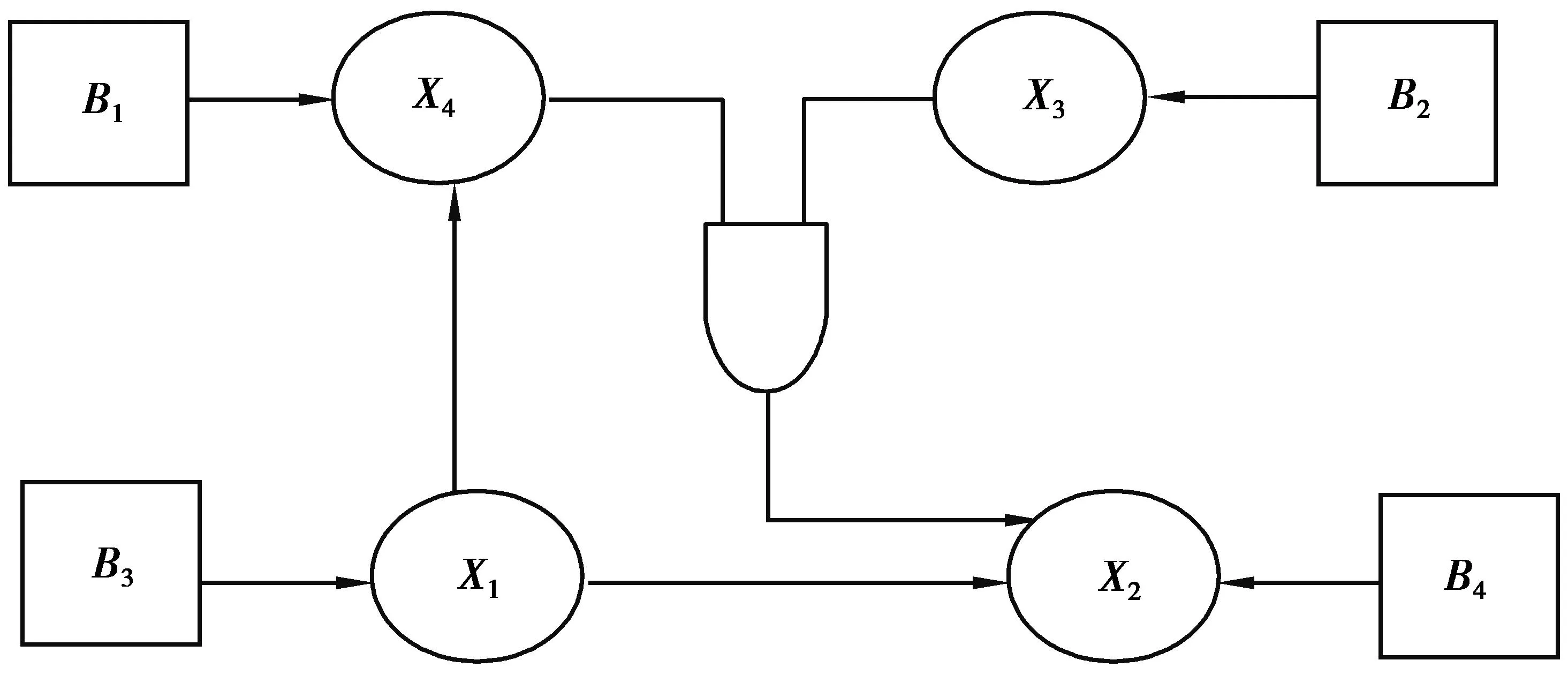
图3　因果图

根据文献[2，4]，可以先将因果图转化得到因果树(图4)，再将T-S模糊门应用到因果树中.在对因果图进行微因果树化时(图5)，微因果树的菱形为与节点相邻的节点事件，圆圈为与节点事件相邻的基本事件.它的实质实际是将节点事件以树根的形式呈现出来的过程.

在转换后的因果树中，用B=(B1，B2，B3，B4)来表示基本事件，T-S门i(1，2，3)用yi(i=1，2，3)表示，X=(X1，X2，X3，X4)表示上级事件，一般情况下，由部件状态计算上级故障的概率，假设X1～X4，B1～B4的故障状态为(0，0.5，1)，隶属函数取三角形模糊数，设Bi(i=1，2，3，4)的模糊子集为Bi=(ni，mi，ri)，用来表示基本事件的故障度.根据经验和专家数据，可得到T-S模糊门，如表1-表3所示.

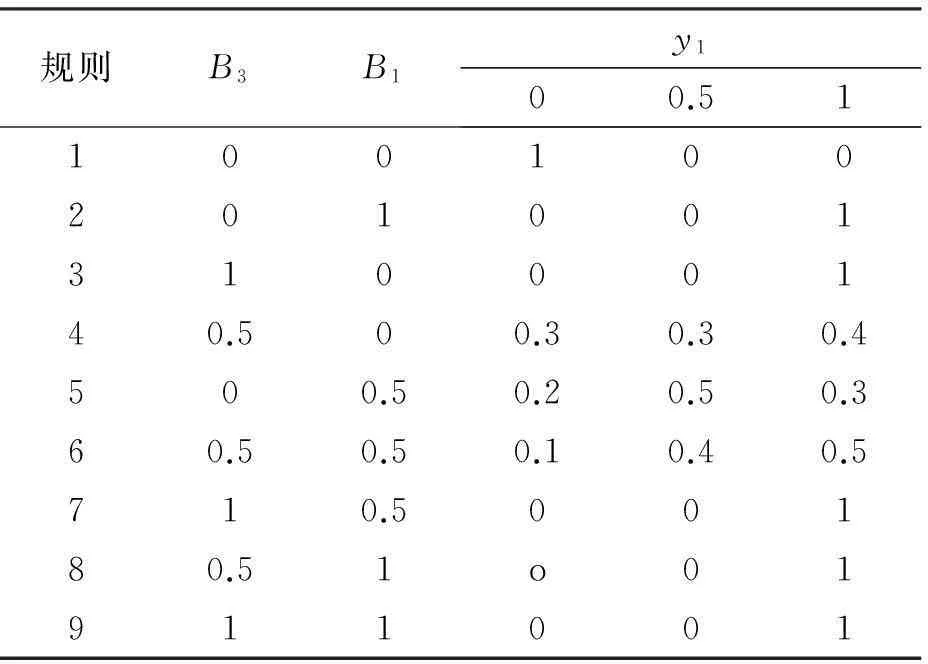
表1　T-S门1

表2　T-S门2

表3　　T-S门3

图4　因果图3对应的因果树

图5　因果图3对应的微因果树

从表1-表3中可以得到，每一行代表一条规则，例如表3中的规则1表示：如果y1为0，y2为0，则y3为0的可能性为1，为0的可能性为0，为1的可能性为0.若在此因果树中，假设知道基本事件的模糊子集为Bi=(ni，mi，ri)，为部件故障状态为1的模糊集，假设故障为0.5时的模糊子集与部件状态为1的模糊子集相同.因此根据式(1)，(2)，可以计算出系统的模糊可能性，即

(4)

若已知基本事件Bi(i=1，2，3，4)的故障状态，通过式(3)(4)，可以计算出各种故障状态的可能性.

3结论

在T-S模糊门运用到故障树的基础上，将T-S模糊门引入到因果图中，由于研究的限制，只能运用于具有确定关系的因果图中，并将因果图转换成因果树进行分析.在分析过程中，将T-S模糊门及运算公式运用到因果树中，通过验证，有一定的适用性.对于不确定因果关系的因果图，T-S模糊门引入还需要进一步的研究.

参考文献：

[1] 宋华，张洪钺，王行仁.T-S模糊故障树分析方法[J].控制与决策，2005，20(8)：854-859

[2] 姚成玉，张荧驿，王旭峰，等.T-S模糊故障树重要度分析方法[J].中国机械工程，2011，47(12)：1261-1268

[3] 梁新元，王洪春，石庆喜，等.因果图向故障树转换的研究[J].计算机仿真，2005，22(12):67-70

[4] 梁新元，张勤.故障树向因果图的转换的研究[J].计算机仿真，2005，22(10):144-146

[5] 姚成玉，张荧驿，王旭峰，等. T-S模糊重要度分析方法研究[J].机械工程学报，2011(11):163-168

[6] 李志勇，吴和斌. 液压系统齿轮浆T-S模糊故障树分析[J].机械工程与自动化，2009(2)：102-104

[7] 裴扬，宋笔锋.故障树分析的等效失效概率计算方法[J].机械工程学报，2007，43(9):207-210

[8] 姚成玉，赵静一.基于T-S模型的液压系统模糊故障树分析研究[J].中国机械工程，2009，20(16)：1913-1917

[9] 王永传，郁文贤，庄钊文.一种故障树模糊重要度分析的新方法[J].国防科技大学技术大学学报，1999，21(3)：63-66

Application of T-S Fuzzy Gate in Causality Diagram

YAN Xiao， WAN Hong-chun1

(School of Mathematical Sciences， Chongqing Normal University， Chongqing 401331， China)

Abstract：The fuzzy logic and T-S fuzzy model are introduced into the fault tree analysis， and T-S fuzzy door is used to describe the relations of events， to solve the uncertainty of events relations. T-S fuzzy door is applied in fault tree， and this method is proved to be practical. Both causality diagram and fault tree can be applied in fault diagnosis， and the causality relation can be expressed by diagram. There is a strong resemblance between fault tree and causality diagram， and under certain conditions， fault tree and causality diagram can be transformed into each other. [1] Due to some limitation of this paper， causality diagram in this paper is all certain relation. From the literature[2]， causality diagram transformed from fault tress with no coupling is causality tree， so on the basis of the application of T-S fuzzy door[3] in fault tree， T-S fuzzy door is introduced into causality diagram.

Key words： fault tree; causality diagram; causality tree; T-S fuzzy door