基于虚拟决策单元的排序模型

基于虚拟决策单元的排序模型

汪云林1,3,韩伟一2,葛虹2

(1.北京大学政府管理学院,北京100871;2.哈尔滨工业大学经济与管理学院,黑龙江哈尔滨150001;3.北京大学科技开发部,北京100871)

摘要：本文给出了一种新的决策单元排序方法。基于经典的C2R模型，通过引入一个虚拟的决策单元，形成了一个新的排序模型，按照相对效率值的大小实现了决策单元的排序。实验表明，新排序方法不仅能较好地反映C2R模型的计算结果，而且可避免超效率方法造成的相对效率值偏大的弊端。新的排序方法依据充分、简单方便，同时体现了整体的决策效率。

关键词：数据包络分析;排序;决策单元;虚拟;有效单元

收稿日期：2014-03-02

基金项目：国家自然科学基金资助项目(71101037);中央高校基本科研业务费专项资金资助(HIT.HSS.201406)

作者简介：韩伟一(1974-),男,副教授,硕士生导师。

中图分类号：O221;N224.0文章标识码：A

Ranking Model Based on the Virtual Decision-making Unit

WANG Yun-lin1,3, HAN Wei-yi2,*, GE Hong2

(1.SchoolofGovernment,PekingUniversity,Beijing100871,China; 2.SchoolofEconomicandManagement,HarbinInstituteofTechnology,Harbin150001,China; 3.OfficeofScience&Technology,PekingUniversity,Beijing100871,China)

Abstract:In the paper, a ranking method is presented for decision-making units. Based on the classical C2R model, a new ranking model is obtained by introducing a virtual decision-making. According to the value of relative efficiency, all decision-making units can be ranked. Experiments show that the ranking method can reflect the computational result of C2R model better. Moreover，it can’t make the value of relative efficiency too large like the super-efficiency method. Not only does the method provide a sufficient basis, but it is very simple. It is deserved to note that it has embodied the systemic efficiency.

Key words:data envelopment analysis; rank, decision-making unit; virtue; efficient unit

0引言

数据包络分析(DEA)作为一种基于线性规划的非参数评价方法，已被广泛地应用到军事、教育、物流、科研、环境保护等众多领域。然而，根据相对效率值，C2R、BC2等经典的DEA模型仅能把决策单元区分为有效单元和非有效单元[5,6]。由于有效单元的相对效率值均为1，因而无法实现对决策单元的完全排序。近年来，对决策单元进行排序一直是DEA领域的研究热点，已经涌现了大量的科研成果。1986年Sexton等人利用交叉系数矩阵尝试对决策单元进行排序[8]。1993年Anderson和Petersen给出了超效率的排序方法[9]。1995年Khouja提出了两阶段法[7]。1996年Torgersen提出了基准点排序方法[10]。2002年Adler等人把所有的排序方法归纳为五种类型[11]，对决策单元排序的相关研究进行了总结。国内在决策单元排序方面也涌现了一些研究成果，参见文献[1～5]。总体来看，这些排序方法都存在明显的不足之处。本文无意克服这些方法的不足，而是将从一个全新的角度提出一种新的排序方法。这种排序方法基于经典的C2R模型，通过引入一个特殊的决策单元，最终实现所有决策单元的排序。这个引入的决策单元反映了总产出与总投入的比值关系，能够体现整体决策效率。

1经典的C2R模型

设DEA系统中有n个决策单元，每个决策单元有m个投入指标、s个产出指标。所有决策单元的投入指标构成投入矩阵X，所有决策单元的产出指标构成产出矩阵Y, 如下

其中xij为第i个决策单元的第j个投入指标，yik为第i个决策单元的第k个产出指标。为了表述方便，特称向量Xi=(xi1,xi2,…,xim)T为决策单元i的投入向量，向量Yi=(yi1,yi2,…,yis)T为决策单元i的产出向量。下面给出经典的C2R模型，如下:

maxZ=ωY0

(1)

其中Y0和X0为所评价决策单元i0(1≤i0≤n)的产出向量和投入向量，向量ω=(ω1,ω2,…,ωs)中的各分量均为变量，为产出向量的权重向量，向量ε=(ε1,ε2,…,εm)中的各分量均为变量，为投入向量的权重向量。

由C2R模型可以得到各个决策单元的相对效率值，当值为1时相应的决策单元为有效单元，否则为非有效单元。对于非有效单元，可以根据相对效率值的大小进行排序。而对于有效单元，由于相对效率值均为1无法实现排序。

2新的排序模型

既然很多排序方法可以按照相对效率值的大小对非有效的决策单元进行排序，那么只需把要评价的n个决策单元全部转换为非有效的决策单元即可。基于这个思路，本文将在原有n个决策单元的基础上，新引入一个决策单元。在新提出的排序模型中，这个新引入的决策单元将是唯一的有效单元，原有的n个决策单元均为非有效单元。问题的关键是，这样的决策单元如何定义才能不影响原有决策单元的效率顺序，或更好地反映原有评价系统的总体关系。

对引入的决策单元作如下定义，设该单元的产出向量为Yt，投入向量为Xt，令

Yt=Y1+Y2+…+Yn,Xt=(X1+X2+…+Xn)/a

(2)

或Yt=(Y1+Y2+…+Yn)*a,Xt=X1+X2+…+Xn

(3)

这里α为足够大的正实数。无疑ωYt/εXt反映了总投入和总产出的决策效率。

新的排序模型如下:

maxZ=ωY0

(4)

对于新模型，只要a足够大，原来所有的决策单元均将成为非有效单元，因为新引入的决策单元将以非常小的投入获得原有的产出，或以原有的收入获得非常多的产出，结论是显然的。

由于新引入的决策单元可采取两种定义，因而有必要证明二者的计算结果是相同的，证明如下

定理1在新排序模型中，新引入的决策单元无论采取式(2)的定义，还是采取式(3)的定义，对于所评价决策单元i0(1≤i0≤n)，经计算得到的相对效率值是相同的。

maxZ=ωY0

(5)

由式(3)得到的模型为

maxZ=ωY0

(6)

模型(5)和模型(6)显然等价。因此，对于决策单元 由两个模型计算所得的相对效率值必然相同。命题得证。

新模型具有如下重要的性质：

定理2对于新排序模型，引入的决策单元为唯一的有效单元，如果当a取值为b时，决策单元i0的相对效率值为ω*Y0，那么当a为hb(h>1)时，决策单元i0的相对效率值为ω*Y0/h。

证明对于新排序模型，设引入的决策单元采取式(3)的定义。它的对偶模型如下

maxZ=θ

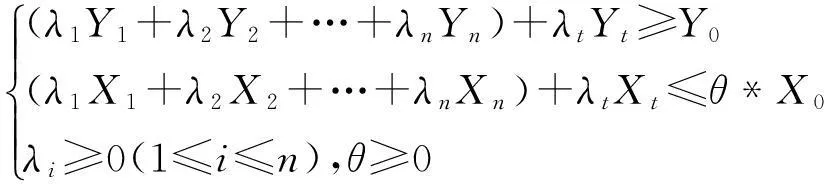
(7)

其中对偶变量λi对应原问题中的约束条件ωYi-εXi≤0，对偶变量λt对应原问题中的约束条件ωYt-εXt≤0，对偶变量θ对应原问题中的约束条件εX0=1。

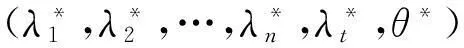
根据定理2，可得如下重要的推论：

推论1在新排序模型中，假定引入的虚拟决策单元为唯一有效单元，对于不同的a，原有的、任意两个不同的决策单元的相对效率值的比值总是恒定的。

证明对于原有的两个决策单元i1和i2，设a取值为b时，相对效率值分别为d1和d2，比值为d1∶d2。当a取值为hb(h>1)时，根据定理2，相对效率值分别为d1/h和d2/h, 比值仍为d1∶d2。命题得证。

定理2和推论1说明, 本文给出的排序方法是稳定的。

诚然，只要新引入决策单元的产出向量足够大，投入向量足够小，均能保证原有的决策单元在新模型中为非有效单元。新引入的决策单元是不是具有任意性呢？答案显然是否定的，因为不同的决策单元将会得到不同顺序的计算结果，这将在下一部分的实验中加以验证说明。

既然新引入决策单元不具有任意性，因此必须要满足一定的原则。C2R模型的本质是尽量实现每一个决策单元的效率最大化，它考虑了个体的局部利益。作为一个决策系统，从整体上也希望实现全局效率最大化。这样一来，在保证整体效率最大化的前提下，再体现个体效率最大化，无疑是一个非常自然的思路。本文对新引入决策单元的定义正是基于上述思路。新引入决策单元不仅将作为唯一的有效单元，而且它的产出向量Yt与投入向量为Xt之比恰是全局效率的体现。

3模型实验

本文将开展3个方面的实验：(1)使用C2R模型计算各决策单元的相对效率，并区分有效单元和非有效单元，为后面的实验提供参考; (2)引入两个不同的决策单元，再使用本文提出的排序模型进行实验，第一个决策单元由本文的定义给出，另外一个决策单元的投入向量和产出向量任意取定，通过比较以说明本文定义的合理性; (3)选用超效率方法和本文的方法进行比较。

3.1采用C2R模型进行实验

由C2R模型计算得到的各决策单元的效率值如下:

表1　采用C 2R模型的计算结果

根据表1，决策单元1和2为有效单元，而决策单元3和4为非有效单元。

3.2采用新排序模型进行实验

在第二个实验中，首先引入新的决策单元5。它的投入向量为(2.2, 1.9)T, 产出向量为(16, 23, 19)T。显然，它的产出向量为四个决策单元的总产出，投入产量经四个决策单元的总投入除以10得到，也就是a取值为10。采用本文的排序模型，计算结果见表2。

表2　采用排序模型和决策单元5的计算结果

根据表2，按照相对效率值大小排序，可得四个决策单元的顺序为：2, 1, 3, 4。这个结果和C2R模型计算结果基本吻合。

再引入新的决策单元6进行实验。它的投入向量为(2.2, 1.9)T, 产出向量为(30, 30, 30)T。显然这样的决策单元是随意定义的。采用本文的排序模型，计算结果见表3。

表3　采用排序模型和决策单元6的计算结果

根据表3，按照相对效率值大小排序，可得四个决策单元的顺序为：2, 3, 1, 4。这个结果与C2R模型计算结果显然是相悖的。决策单元3原为非有效，决策单元1原为有效，当前的计算结果反而颠倒了二者的顺序。

实验2的两个计算结果表明，本文所定义的引入决策单元是合理的。

3.3采用超效率方法进行实验

相对于C2R模型，超效率方法在计算各个决策单元的相对效率时，采用如下的模型

maxZ=ωY0

(8)

其中Y0和x0分别为决策单元i0(1≤i0≤n)的产出向量和投入向量，ω=(ω1,ω2,…,ωs)向量为产出向量的权重向量，向量ε=(ε1,ε2,…,εm)为投入向量的权重向量，ω和ε的各分量均为变量。

采用超效率方法的计算结果，见表4。

表4　采用超效率的计算结果

根据表4，按照相对效率值大小排序，可得四个决策单元的顺序为：1, 2, 3, 4。这个结果和采用新排序模型给出的顺序并不一致。

表5　归一化的计算结果

把表2和表4的计算结果进行归一化处理，分别把四个决策单元的相对效率值除以最大的相对效率值，则得到归一化的计算结果，见表5。

根据表4和表5，有效单元的相对效率值相对偏大，这印证了超效率方法可能高估一些决策单元的相对效率值的说法。理所当然，超效率方法因为高估一些决策单元的相对效率值，将不能正确给出各决策单元的排列顺序。表2和表5的结果说明，本文的方法相对于超效率方法将更合理些。

4结论

本文从强调整体效率最优出发，通过引入一个特殊的虚拟单元，基于经典的C2R模型，提出了一种新的决策单元排序方法。新排序方法具有如下两个特点：(1)新方法依据充分、简单方便，能够正确反映C2R模型的计算结果，相对于超效率方法的计算结果更趋合理；(2)定理2和推论1说明新方法可靠稳定。

参考文献：

[1]刘英平,林志贵,沈祖诒.有效区分决策单元的数据包络分析方法[J].系统工程理论与实践,2006,3:112-116

[2]王军,孙利辉,刘晶.基于虚拟决策单元的DEA全排序方法[J].科研与管理，2009,30(3):198-202

[3]查勇,梁樑等.基于公共权重的集成DEA排序方法[J].中国管理科学,2007,第15卷(专辑):16-20

[4]张天学，张福翔.DEA评价与排序的新方法[J].数学的实践与认识,2002,32(6)：911-919

[5]Chames A, Cooper W, Rhodes E. Measuring the efficiency of decision-making unite[J]. European Journal of Operational Re search, 1978,(2): 429-444

[6]Banker R D, Chames A, Cooper W W. Some models for estimating technical and scale inefficiency in data envelopment analysis[J]. Management Science, 1984,(30): 1078-1092.

[7]Khouja M. The use of data envelopment analysis for technology selection[J]. Computers and Industrial Engineering, 1995, 28(2): 123-132

[8]Sexton T R, Silkman R H, Hogan A G. Data envelopment analysis: critique and extensions[M]. in R H Silkman(Ed.), Measuring Efficiency: An Assessment of Data Envelopment Analysis. Jossey-bass, San Francisco, 1986: 73-104

[9]Anderson P, Petersen N C. A procedure for rank efficient units in data envelopment analysis[M]. Management Science, 1993, 39(10): 1261-1264

[10]Torgerson A M, Forsund F R, Kittelsen S A C. Slack adjusted efficiency measures and ranking of efficient units[J]. The Journal of Productivity Analysis, 1996, 7: 379-398

[11]Adler N, Friedman L, Stern Z S. Review of ranking methods in the data envelopment analysis context[J]. European Journal of Operational Research, 2002, 140: 249-265.