不同流体加速度描述对输液曲管稳定性的影响

2016-01-15胡育佳,李海港

振动与冲击 2015年15期

胡育佳，李海港

(上海理工大学机械工程学院，上海200093)

摘要：在自然坐标系中建立了具有任意初始构型可伸长输液曲管的数学模型并进行了数值模拟。为了便于处理边界条件，引入新的独立变量，采用微分求积法(Differential Quadrature Method,DQM)和分块矩阵的方法求解输液曲管的固有频率。讨论了三种流体加速度表示方法对可伸输液管道稳定性的影响。研究发现，对复杂构型的输液曲管，三者的第一阶固有频率随着流速的增大，差别越来越显著；然而，对于规则构型的输液管道，结果却非常相近。

关键词：输液曲管；微分求积法；固有频率；流体加速度

中图分类号:O327文献标志码：A

基金项目：校企合作项目(20142000237)；国家重点实验室重点项目(ZZ2013-014)

收稿日期：2014-06-18修改稿收到日期：2014-07-30

基金项目：国家自然科学基金(51378442，51278435)

收稿日期：2014-10-22修改稿收到日期：2015-03-11

Effects of different fluid accelerations on stability of curved pipes conveying fluid

HUYu-jia,LIHai-gang(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

Abstract:A dynamic model of an extensible curved pipe with an arbitrary initial configuration was established in an arc coordinate system and its numerical simulation was performed afterwards. A new independent variable was introduced to deal with boundary conditions in order to obtain natural frequencies of curved pipes conveying fluid based on the differential quadrature method (DQM) and the partitioned matrix method. The effects of three fluid accelerations on the stability of the pipes conveying fluid was discussed. It was shown that with increase in fluid velocities, the differences between the first natural frequencies of pipes with complex configuration under three different fluid accelerations become more significant; however, for regular configuration pipes, the effects of different fluid accelerations on pipes’ natural frequencies are small.

Key words:curved pipe conveying fluid; DQM; natural frequency; fluid acceleration

输液管道振动动力学特性的分析，一直是结构动力学问题中一个比较热门的研究课题。这不仅因为输液管道有着广泛的工程应用背景，而且输液管道的振动问题具有重要的理论研究价值。因而，许多学者很早便开始了输液管道相关问题的研究。在工程中，输液管道结构往往是由输液直管和曲管组成，输液直管的研究已经相对成熟，然而输液曲管的研究相对比较少见。

Chen[1-2]较早的提出了半圆形的输液曲管的振动分析模型，该模型假设管道轴向不可伸长，他利用Newtonian[1]和Hamiltonian[2]原理导出了输液曲管的运动微分方程，但是该方程只适用于圆弧形的输液曲管，不能用于变曲率管。倪樵等[3-5]在平面输液曲管的动力学振动方面也作了大量的工作，他们把微分求积法(DQM)成功应用到半圆形输液曲管的振动稳定性分析中。其中，文献[3-4]使用了内部点来处理边界条件，这将对分析复杂问题(特别是具有任意初始构型的管道结构)和计算精度带来一定的影响。在DQM方法的基础上，他们还进一步研究了运动约束下半圆形输液曲管的非线性动力学特性，其中非线性项是由约束运动的条件引入的[5]。Misra等[6-7]使用有限元方法研究了不可伸长和可伸长半圆形输液曲管的振动特性。李宝辉等[8-9]提出了一种求解输液曲管固有频率的计算方法，即波动法，研究了不可伸和可伸输液管道的稳定特性。Jung等[10]基于Hamiltonian原理，由物质导数推导出了一种新的轴向可伸长半圆形输液曲管的流体加速度表示方法。

然而，在可伸输液曲管稳定性的研究中，一方面流体加速度描述方法比较混乱，有的流体加速度表示方法只能用来分析不可伸长输液管道的情况，对于可伸长的情况并不适用，否则将对分析结果带来偏差。比如，文献 [6-9, 11-12]中的流体加速度都是基于Newtonian原理推导的一种表示方法，这种描述方法只适用于不可伸长的情况[6, 8]，不能用来分析可伸长的输液曲管[7, 9, 11-12]。另一方面，由于分析模型和计算方法的限制，以往的研究主要集中在半圆形或圆弧形输液曲管上，对于复杂构型输液曲管的研究很少。

本文将在以弧长为参数的自然坐标系中建立轴向可伸任意初始构型输液曲管平面内振动的运动微分方程，利用微分求积法和分块矩阵方法求解具有任意初始构型的输液曲管的固有频率。讨论了三种输液曲管流体加速度表示方法的不同，分析流体加速度对可伸长规则构型和复杂构型输液管道稳定性的影响。

1流体加速度的描述

在可伸长输液管道的振动稳定性分析中，流体加速度的描述方法有多种，本文总结了三种流体加速度表示方法，分别为

(1a)

(1b)

(1c)

式中：R为曲率半径，∂(□)/∂φ为未知量对圆心角φ的一阶偏导数，ws,wη分别为弧线坐标系下切向和法向的位移，as,aη分别为流体的切向和法向方向上的加速度，∂(□)/∂t为未知量对时间t的一阶偏导数，v为流体流速。式(1a)为Jung等[10]推导出的新流体加速度表示方法，推导方法为Hamiltonian方法，考虑了轴向伸长的影响；式(1b)为流体加速度，推导方法为Newtonian方法，忽略了轴向伸长；式(1c)是由Hamiltonian方法得到的，也忽略了轴向伸长。所以第一种加速度表达比后两种流体加速度更合理。为了方便讨论，把这三种流体加速度表示法依次称为Case Ⅰ、Case Ⅱ、Case Ⅲ。

此外，流体加速度Case Ⅰ的合理性，也可以通过可伸长输液直管的流体加速度[13-15]体现出来，该加速度可以表示为

(2)

式中:s为输液曲管的弧长，∂s可用R∂φ表示。当曲率半径R→+∞时，则圆弧形的输液管道的流体加速度变成了输液直管的情况，将三种情况下的流体加速度退化成输液直管的情况，且R∂φ可用∂s表示。可以发现，只有Case Ⅰ的退化公式与公式(2)输液直管的流体加速度完全一致，Case Ⅱ和Case Ⅲ则不能，这也说明了Case Ⅰ的完备性。本文在讨论可伸长时采用了Case Ⅰ的流体加速度表示方法，分析不可伸长时使用了Case Ⅱ。且在分析求解中需把三种加速度表示方法转化到弧坐标下，其中1/R=∂θ0/∂s。

2数学建模

假设输液曲管为曲梁模型，则输液曲管的几何关系[16]可表示为

(3a)

(3b)

式中:R1(s)-1为轴线的伸长率，θ和θ0分别为曲管变形后和初始构型上任意点处的切向方向与y轴的夹角。在小变形假设的情况下，转角满足以下条件

(4)

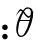
(5a)

(5b)

式中，当R1-1≠0时，表示管道轴向是可伸长的；R1-1=0，则表示忽略管道轴向伸长。

对于输液管道的稳态动力学问题，本文的平衡方程将建立于输液管道变形前。从流体和输液管上截取长度为δs的单元作为研究对象，受力分析如图1所示。

图1　流体管道单元受力分析 Fig.1 The forces diagram of fluid and pipe elements

假设输液管道的材料是线性的，且输液管道轴向可伸长，由式(4)和式(5a)，则由线弹性本构关系推导得到为

(6a)

(6b)

式中，E为管道的杨氏模量，Ap为管道截面面积，EI、EAp分别为抗弯和抗拉刚度。管道的切向、法向和弯矩运动微分方程为

(7a)

(7b)

(7c)

式中:M,Np,Q分别为截面的弯矩、轴力和剪力，mp为单位长输液管的质量，g为重力加速度，fs和fη为管道和流体接触面上的切向和法向作用力。

流体的切向和法向运动微分方程为

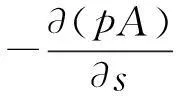
(8a)

(8b)

式中:p为流体的压力，A为流体的截面面积，mf为单位长流体的质量。对于管道可伸长情况，本文采用Case Ⅰ的流体加速度，可表示为

(9a)

(9b)

从公式(8a)中提取fs代入公式(7a)，从公式(8b)中提取fη代入公式(7b)，整理后得

(10a)

(10b)

式中:Fs,Fη分别为管道和流体的重力、压力和流体的惯性力在切向s和法向η方向上投影的合力，可以表示为

Fs=mgcosθ0+mfas+∂(pA)/∂s,

Fη=mgsinθ+mfaη-(pA)∂θ0/∂s

(11)

引入如下的无量纲条件

(12)

把控制方程(5a) 、(10a)和(10b)无量纲化，且整理可得

(13b)

(13c)

两端固定的无量纲边界条件为

Ws(0)=Ws(1)=Wη(0)=Wη(1)=

(14)

3求解

采用微分求积方法和分块矩阵法求解在边界条件为(14)下的输运管道的控制方程(13)。微分求积方法的基本原理是将函数对某方向的自变量的偏导数近似表达为沿自变量方向各离散点上相应函数值的加权和。为了保证计算精度，如果没有特别说明，本文将采用Chebyshev-Lobatto多项式零点的布点方式，取布点数N=21[17]

将控制方程(13) 和边界条件(14)离散得

(15a)

(15b)

(15c)

(15d)

(16)

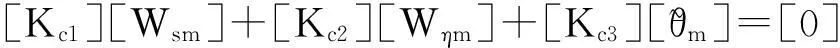
由方程(17c)得

(18)

其中[K1]=[Kc3]-1[Kc1],[K2]=[Kc3]-1[Kc2]，把式(18)分别代入式(17a) 和(17b)得

[ZKa1][Wsm]+[ZKa2][Wηm]=[0]

(19a)

[ZKb1][Wsm]+[ZKb2][Wηm]=[0]

(19b)

其中[ZKa1]=[Ka1]-[Ka3][K1],[ZKa2]=[Ka2]-[Ka3][K2]，[ZKb1]=[Kb1]-[Kb3][K1]，[ZKb2]=[Kb2]-[Kb3][K2]。将(19a)、(19b)合并得

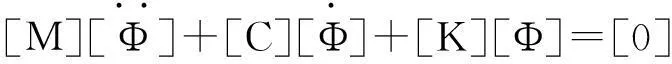
(20)

(21)

(22)

(23)

(1)给定一个初始构型y=f(x) (a≤x≤b)；

(3)采用切比雪夫零点布点方式得到每个点的坐标Si(0≤S≤1)；

(5)由无量纲初始构型Y=f(x)求解布点处的坐标(Xi,Yi)；

(6)由dY/dX=tan(π/2-θ0)计算布点处的转角

(24)

4数值算例

为了进一步比较三种流体加速度，该部分将研究这三种流体加速度对输液管道振动特性的影响。首先验证本文理论和编程的有效性，然后分别采用这三种流体加速度表示方法研究轴向可伸长规则构型输液管道(如输液直管和圆弧形管道)和复杂构型输液管道(如椭圆形和有初始构型缺陷的圆弧形管道)的稳定特性。为了方便讨论，无量纲固有频率ω*可表示为ω*=Ω(R0/l)2=Ω/σ2，无量纲流速V*=V/σ(σ=l/R0，R0=0.5 m)，其中ω为输液曲管的有量纲固有频率。此外，本文的边界条件为两端固定。图2给出了两端固定的圆弧形或椭圆形的输液管道。其中，R为曲率半径，L0为跨距，φ为圆心角，a,b分别为椭圆的长轴和短轴。

图2　输液曲管示意图 Fig.2 The sketch of curved pipe

4.1结果验证

为了说明本方法的有效性，首先研究了输液直管和输液曲管稳定特性，并与已有结果进行比较，如图3所示。图3(a)给出了可伸长输液直管前三阶固有频率随流速的变化，可以发现本文的结果与Lee[13]的研究结果吻合得很好。当无量纲流速V=6.28时，输液管道发生失稳，该临界流速与Lee的相等，这也证明本文输液管道分析模型的有效性。需要说明的是输液管道的物理特性以及尺寸参数见文献[13]，且该模型的流体加速度表示方法为Case Ⅰ。

图3(b)研究了不可伸长半圆形输液管道(φ=π,R=0.5 m,L0=1.0 m)的前四阶固有频率随流速的变化。管道的物理特性以及尺寸参数[8]分别为单位长管道和流体的质量为mp=mf=1.78 kg/m，杨氏模量E=10 GPa，截面惯性矩I=7.491×10-8m4。可以发现，本文结果与Misra[6]的结果非常相近，此分析模型的流体加速度为Case Ⅱ。由图3(b)的分析结果进一步验证了本文的分析模型以及编程的正确性。

图3　输液直管和半圆形曲管结果验证 Fig.3 Verification results of straight pipe and semi-circle pipe conveying fluid

图4　可伸半圆形输液管道无量纲固有频率随无量纲速度的变化 Fig.4 Dimensionless frequencies of an extensible semi-circular pipe as functions of the dimensionless flow velocity

4.2不同流体加速度描述对管道稳定性的影响

图4、图5、图6和表1研究了不同初始构型输液曲管的振动特性。这里需要说明的是，本部分输液管道物理特性和尺寸参数与图3(b)的相同，并取Ap/I=2.5×104m-2。图4给出了三种流体加速度表示方法对可伸长半圆形输液曲管(φ=π,R=0.5 m,L0=1.0 m)稳定性的影响。可以发现，随着流速的增大，三种情况下得到的结果几乎完全一致。图5研究了半椭圆形输液管道(a=0.5 m,b=0.6 m,L0=1.0 m,φ=π)在三种流体加速度下的结果比较。结果发现，三种流体加速度所对应的临界流速V*分别为2.72、2.605和2.604。Case Ⅲ和Case Ⅱ的临界流速几乎相等，且两种情况下的前三阶固有频率随流速变化的趋势几乎完全一致。而Case Ⅱ相比Case Ⅰ的临界流速偏小了-4.23%，二者的第一阶固有频率随着流速的增大，差别越来越显著。三种情况的第二、三阶固有频率差别比较小。

图5　可伸半椭圆形输液管道无量纲固有频率随无量纲速度的变化 Fig.5 Dimensionless frequencies of an extensible semi-elliptical pipe as functions of the dimensionless flow velocity

参考文献图6研究了三种流体加速度对一种有初始结构缺陷的半圆形输液曲管稳定性的影响。[18]，给出输液曲管的初始构型表达式为

A1cos[π(x-0.5L0)/L0],(0≤x≤1.0 m)

(25)

图6　可伸有初始结构缺陷半圆形输液管道无量纲固有频率随无量纲速度的变化 Fig.6 Dimensionless frequencies of an extensible semi-circular pipe with initial structural defect as functions of the dimensionless flow velocity

管道模型CaseⅠCaseⅡCaseⅢCaseⅡ和Ⅰ区别CaseⅢ和Ⅱ区别a=b=0.5m3.0033.0033.00300a=0.5m,b=0.4m3.3173.4023.4052.56%0.09%a=0.5m,b=0.6m2.722.6052.604-4.23%-0.04%A1=-0.1m,R=0.5m3.2613.5543.5588.98%0.11%A1=0.1m,R=0.5m2.7392.5232.515-7.89%-0.32%Straightpipe3.1443.1443.14400

表1列出了不同初始构型输液管道的临界流速。可以发现对于规则构型的输液管道，例如输液直管和半圆形管道，三种流体加速度的临界流速相等。对于半椭圆形输液曲管和有初始结构缺陷的半圆形管道，Case Ⅰ和另外两种Case Ⅱ、Case Ⅲ的临界流速差别比较明显，然而Case Ⅱ和Case Ⅲ的临界流速却非常相近。

5结论

本文在以弧长为参数的坐标中建立了具有任意初始构型输液曲管的运动微分方程。方程中包含三个变量，能够用来精确处理边界条件。采用微分求积法和分块矩阵的方法进行求解。首先讨论了三种加速度推导方法和退化到输液直管时的不同，发现第一种流体加速度描述方法更完备。分析了三种流体加速度表示方法对轴向可伸长规则构型管道和复杂构型输液管道动力学特性的影响。数值结果表明，对于规则构型的输液管道，三种流体加速度的结果非常相近，区别很小。然而，在研究复杂构型的输液曲管时，第一种流体加速度和另外两种加速度的第一阶固有频率随着流速的增大，差别越来越明显。因此，对于轴向可伸长复杂构型的输液曲管稳定性问题，应选取描述比较完备的第一种流体加速度表示方法。

参考文献

[1]Chen S S. Vibration and stability of a uniformly curved tube conveying fluid [J]. Journal of Acoustical Society of America, 1972, 51: 223-232.

[2]Chen S S. Flow induced in plane instabilities of curved tubes [J]. Nuclear Engineering and Design, 1972, 23: 29-38.

[3]倪樵，张惠兰，黄玉盈. DQ法用于具有弹性支承半圆形输液曲管的稳定性分析[J]. 工程力学，2000,17(6): 59-64.

Ni Qiao, ZHANG Hui-lan, HUANG Yu-ying. Differential quadrature for the stability analysis with semi circular pipe conveying fluid with spring support [J]. Engineering Mechanics, 2000, 17(6): 59-64.

[4]Wang Lin, Ni Qiao. In plane vibration analysis of curved pipes conveying fluid using the generalized differential quadrature rule [J]. Computer and Structures, 2008, 86: 133-139.

[5]Wang Lin, Ni Qiao. Nonlinear dynamics of a fluid-conveying curved pipe subjected to motion-limiting constraints and a harmonic excitation [J]. Journal of Fluids and Structures, 2008, 24: 96-110.

[6]Misra A K, Païdoussis M P, Van K S. On the dynamics of curved pipes transporting fluid. Part I: inextensible theory [J]. Journal of Fluids and Structures, 1988, 2: 221-244.

[7]Misra A K, Païdoussis M P, Van K S. On the dynamics of curved pipes transporting fluid. Part II: extensible theory [J]. Journal of Fluids and Structures, 1988, 2: 245-261.

[8]李宝辉，高行山，刘永寿,等. 输液曲管平面内振动的波动方法研究[J]. 固体力学报，2012,33(3): 302-308.

LI Bao-hui, GAO Hang-shan, LIU Yong-shou,et al. Wave propagation method for in plane vibration of curved pipe conveying fluid [J]. Journal of Solid Mechanics, 2012, 33(3): 302-308.

[9]李宝辉，高行山，刘永寿. 轴向可伸输液曲管平面内振动的波动方法研究[J]. 振动与冲击，2013,32(8):128-142.

LI Bao-hui, GAO Hang-shan, LIU Yong-shou. Wave propagation method for in plane vibration of an axially extensible curved pipe conveying fluid [J]. Journal of Vibration and Shock, 2013,32(8): 128-142.

[10]Jung D H, Chung J T, Yoo H H. New fluid velocity expression in an extensible semi-circular pipe conveying fluid [J]. Journal of Sound and Vibration, 2007, 304:382-390.

[11]Dupuis C, Rousselet J. The equations of motion of curved pipes conveying fluid [J]. Journal of Sound and Vibration, 1992, 153: 473-489.

[12]Doll R W, Mote C D. On the dynamic analysis of curved and twisted cylinders transporting fluids [J]. Journal of Pressure Vessel Technology, 1976, 98: 143-150.

[13]Lee S I, Chung J. New nonlinear modeling for vibration analysis of a straight pipe conveying fluid [J]. Journal of Sound and Vibration, 2002, 254(2): 313-325.

[14]Semler C, Li G X, Paidoussis M P. The non-linear equations of motion of pipes conveying fluid [J]. Journal of Sound and Vibration, 1994, 169: 577-599.

[15]Semler C, Paidoussis M P. Non-linear analysis of the parametric resonances of a planar fluid-conveying cantilevered pipe [J]. Journal of Fluids and Structures, 1996, 10: 787-825.

[16]Hu Yu-jia, Yang J, Kitipornchai S. Snap-through and pull-in analysis of an electro-dynamically actuated curved micro-beam using a nonlinear beam model[J]. Journal of Sound and Vibration, 2013, 332: 3821-3832.

[17]Hu Yu-jia, Zhu Yuan-yuan, Cheng Chang-jun. Differential-algebraic approach to large deformation analysis of frame structures subjected to dynamic loads [J]. Applied Mathematics and Mechanics, 2008, 29(4): 441-452.

[18]Kitipornchai S, Yang J, Liew, K M. Semi-analytical solution for nonlinear vibration of laminated FGM plates with geometric imperfections [J]. International Journal of Solids and Structures, 2004, 41: 2235-2257.

附录A