反向旋转双转子系统滞后特性分析
2016-01-15符毅强,陈予恕,侯磊等
反向旋转双转子系统滞后特性分析
符毅强1,陈予恕1,侯磊1,李忠刚1,2
(1.哈尔滨工业大学航天学院,哈尔滨150001; 2.哈尔滨工业大学机电工程学院,哈尔滨150001)
摘要:建立了考虑中介轴承非线性力的简化双转子模型,应用Matlab进行了数值计算,发现系统升、降速幅频曲线存在明显的滞后跳跃现象,并且在相同参数条件下,高、低压转子的滞后特性相似。进一步分别研究了转速比,中介轴承的径向间隙以及阻尼比对系统滞后特性的影响。研究发现转速比绝对值的增大使跳跃幅度逐渐增大但滞后区大小只有微弱的减小,并且使系统的临界转速逐渐减小,滞后区向左移动;径向间隙的增大使系统的滞后区逐渐增大但跳跃幅度几乎不变,而且对系统临界转速的影响较小;阻尼比的增大使系统的滞后区和跳跃幅度逐渐减小,并且使系统的临界转速减小,滞后区向左移动。该研究结果有助于进一步认识中介轴承对双转子系统振动特性的影响。
关键词:反向旋转;双转子;中介轴承;滞后;跳跃现象;临界转速
中图分类号:V23文献标志码:A
基金项目:总装武器装备预研基金(9140A27020214JB14436)资助项目
收稿日期:2014-12-19修改稿收到日期:2015-03-11
基金项目:国家自然科学基金(51275079);中央高校基本业务费专项科研基金(N110403009);新世纪优秀人才支持计划(NCET-10-0301)资助项目
收稿日期:2014-04-24修改稿收到日期:2014-07-06
A counter-rotating dual-rotor system’s hysteretic characteristics
FUYi-qiang1,CHENYu-shu1,HOULei1,LIZhong-gang1,2(1.School of Astronautics, Harbin Institute of Technology, Harbin 150001, China;2.School of Mechatronic Engineering, Harbin Institute of Technology, Harbin 150001, China)
Abstract:A dynamic model of a dual-rotor system with nonlinear force of intermediary bearings was built, and Matlab was used for the numerical calculation. It was shown that there are obvious hysteretic jumping phenomena in the amplitude-frequency curves of the system’s speed-up and speed-down; the hysteretic characteristics of the high pressure rotor are similar to those of the low pressure rotor under the same parameters. Furthermore, the influences of speed ratio of high pressure rotor to low pressure one, intermediary bearing’s radial clearance and damping ratio on the system’s hysteretic characteristics were studied, respectively. The results showed that the increase in speed ratio causes a larger jump but the hysteretic region shrinks slightly and the critical speed decreases, the hysteretic region moves to the left; the larger the intermediary bearing’s radial clearance, the wider the hysteretic region, but the jump amplitude almost unchanges, and its effect on the critical speed is very small; the larger the damping ratio, the smaller the system’s hysteretic region, the jump amplitude and the critical speed, the hysteretic region moves to the left. The study results were helpful to a further understanding the effect of intermediary bearings on the vibration features of dual-rotor systems.
Key words:counter-rotating; dual-rotor; intermediary bearing; hysteresis; jump; critical speed
因为双转子的涡轮和压气机在减轻气流喘振方面相比单转子结构具有很大的优势,故现代航空发动机多采用双转子结构。由于高、低压转子反向旋转有利于减小转子陀螺力矩的影响,还可以降低机匣负荷,提高飞机的机动性,所以高、低压转子反向旋转的双转子结构近年来受到高度重视。英国“鹞”式战机上的“飞马”发动机、美国F22战机上的F119发动机等都是反向旋转双转子发动机。因此,研究反向旋转双转子系统的动力学特性很有现实意义。
目前对双转子系统动力学的研究主要有双转子系统临界转速的计算、双转子系统的动平衡、双转子系统耦合动力学等[1]。Ferraris等[2-3]阐述了有限元法和模态截断法在转子动力学分析上的引用,分析了带有机匣的双转子系统并对部分结果进行了试验验证。Gupta等[4]对反向旋转双转子试验器的动力学特性进行了研究,应用传递矩阵法计算了该反向旋转双转子系统的不平衡响应,并对该系统的临界转速、振型和不平衡响应进行了试验研究。
国内也有很多学者对反向旋转双转子系统进行了研究,罗贵火等[5-7]通过计算分析和试验研究了反向旋转双转子的稳态响应,结果表明航空发动机采用反向旋转双转子系统,有助于减小转子整体陀螺力矩对飞机的影响,降低机匣负荷,提高飞机的机动性能,此外他们还对反向旋转双转子系统进行了非线性响应分析。晏砺堂等[8]结合理论分析、模型试验与某机实测结果的研究,发现双转子发动机因有两个不同频的激振源,发生动静件碰摩时,除出现转子的基频振动外,当发生偏摩时还会出现多种倍频和分频振动以及两转子转速频率的多种复合频率的振动。Hu等[9]建立并研究了一个具有五个自由度的双转子航空发动机模型,并与其他两个模型进行了比较,结论表明转子的旋转自由度和支撑的非线性对系统的动力学仿真具有很大的影响。于海等[10]根据航空发动机低压转子系统建立了具有26个自由度的含有裂纹故障的高维非线性动力学模型,引进改进的POD方法成功将该系统降为具有两个自由度含有特征的低维非线性系统,还利用C-L方法对其进行了分岔分析,讨论了系统参数与系统动态行为之间的关系,得到了裂纹转子各种不同分岔模式,得到了裂纹二分之一亚谐共振条件下的非线性动力学模型,准确反映了裂纹转子的动力学特征。邓四二等[11]建立了含滚动轴承动力学与转子动力学耦合以及高、低压转子间耦合的滚动轴承-双转子系统动力学方程,计算与分析结果表明中介轴承和支承轴承的径向游隙与滚子数量对转子系统运行的平稳性有较大的影响;中介轴承径向游隙较小时转子系统振动量较小且运行较平稳,但中介轴承保持架打滑率会提高;减小中介轴承滚子数量可降低保持架打滑率,但转子系统的振动量会增大;支承轴承滚动体数量增多有利于转子系统运行的平稳性。
然而,在以上研究中,未有对双转子系统滞后特性的报道。本文借用文献[5]的双转子模型,通过数值计算发现系统升降速幅频曲线存在滞后特性,随后分析了转速比,中介轴承的径向间隙以及阻尼比对系统滞后特性的影响。
1转子系统模型
简化的双转子模型[5]如图1所示,内转子代表低压转子,由轴承A,D支撑,外转子代表高压转子,由轴承B,C支撑,内外转子由中介轴承即轴承C联接,中介轴承的存在使双转子系统具有了复杂的非线性动力学特性。其中,内转子轴半径为R1,盘半径为R2,盘厚度为e1。外转子轴内壁半径为R3,外壁半径为R4,盘半径为R5,盘厚度为e2,各轴段长度如图1所示。

图1 简化的双转子模型 Fig.1 Schematic of simplified dual-rotor model
1.1位移表达式
令x1(t),y1(t)分别为内转子盘形心的水平和竖直方向的位移,x2(t),y2(t)分别为外转子盘形心的水平和竖直方向的位移,并将xi(t),yi(t)(i=1,2)简化表示为xi,yi(i=1,2)。设内转子轴上任意一点x和y方向的位移分别为:
u1(z,t)=f1(z)x1(t)
(1)
w1(z,t)=f1(z)y1(t)
(2)
式中:f1(z)为位移函数,定义为内转子轴上任意一点的位移与内转子盘位移的比。假设内转子轴上任意一点x,y方向的弯曲角度分别为θ1,ψ1,在小变形的情况下即θ1,ψ1很小时,其表达式可写为:
(3)
(4)
同样,设外转子轴的x,y方向的位移分别为u2(z,t),w2(z,t),x,y方向的弯曲角度分别为θ2,ψ2,可得:
u2(z,t)=f2(z)x2(t)
(5)
w2(z,t)=f2(z)y2(t)
(6)
(7)
(8)
1.2中介轴承模型

图2 滚动轴承模型 Fig.2 Rolling bearing model
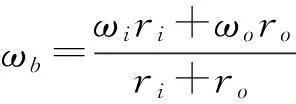
(9)
其中:
δj=[f1(L4)x1(t)-f2(L4)x2(t)]sinθj+
[f1(L4)y1(t)-f2(L4)y2(t)]cosθj-q0
(10)
(11)
(12)
式(9)~式(12)中:Qx,Qy分别为轴承在x,y方向的非线性力,Kb为Hertz接触刚度,δj为第j个滚动体的径向弹性接触变形,θj为第j个滚动体的转动角度,q0为轴承的径向间隙,H(δj)为Heaviside函数,它表达了滚珠与轴承外圈的接触情况。
1.3运动微分方程的建立
由转子动力学理论[13-14]和拉格朗日方程可导出图1所示双转子模型的运动微分方程为:
(13)
(14)
(15)
(16)
以上方程中各参数表达式如下:
(17)
(18)
(19)
(20)
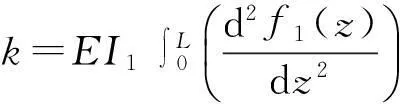
(21)
其中:mu1,mu2分别为内外转子盘的不平衡质量,d1,d2分别为内外转子不平衡量的偏心距,ω1,ω2分别内外转子的转速,W1,W2分别为内外转子的重力,c1,c2分别为内外转子的粘性阻尼系数,MD1,MD2分别为内外转子盘的质量,IDX1,IDX2分别为内外转子相对x轴的转动惯量,ρ为材料密度,S1,S2分别为内外转轴的截面积,I1,I2分别为内外转轴的截面惯性矩,k为内轴的刚度。
1.4无量纲方程
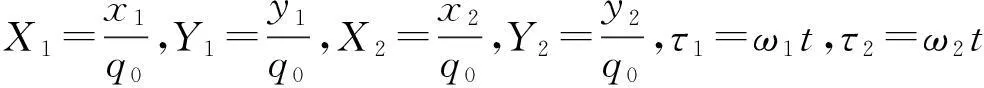
(22)
a4sin(τ1)-a5Qy-a6
(23)
(24)

(25)
其中:
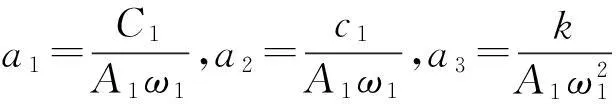

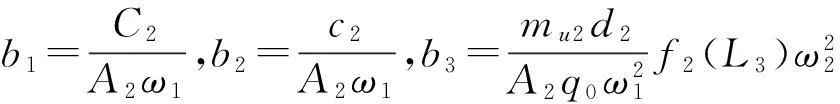
1.5转子系统参数
根据文献[6],转子系统参数如下:
L=1.0 m,L1=0.748 m,L2=0.34 m,
L3=0.50 m,L4=0.68 m,M1=7.2256 kg,
M2=7.306 7 kg,e1=e2=0.02,R1=0.01 m,
R2=0.1 m,R3=0.018 m,R4=0.022 5 m,
R5=0.113 m,ρ=7 754 kg/m3,
E=2.06×1011Pa,ri=0.031 m,
ro=0.046 8 m,Nb=9 ,q0=5×10-6m,
Kb=1.334×1010N·m-1.5
2数值计算结果及分析
2.1转子系统的滞后特性


图3 内、外转子升速、降速的频谱图 Fig.3 Spectrogram of inner rotor for running up and running down
进一步展示系统振动能量的强弱,用振动响应的有效值表示振幅,即:
(26)

图4 内、外转子的升降速幅频曲线 Fig.4 Amplitude-frequency curve of inner and outer rotor for running up and running down
式中:r1,r2分别为内外转子振动响应的有效值(以下称之为振幅)。将内转子转速ω1作为横坐标,得到内外转子的升、降速幅频曲线分别如图4(a),图4(b)所示。图中,虚线代表升速过程,实线代表降速过程,从图中可以看出内外转子振动过程中均存在跳跃现象,而且外转子的跳跃幅度要比内转子的大得多。另外,该系统存在较大的滞后区,而且内外转子的滞后区大小相近。
2.2转速比对滞后特性的影响

图5 转速比对滞后特性的影响 Fig.5 Speed ratio effects on hysteresis
当阻尼比ξ=0.02,径向间隙q0=5×10-6m,高、低压转子的转速比分别为λ=-1.01,λ=-1.1,λ=-1.2时内转子的滞后特性如图5所示(外转子性质相似,不再具体给出,以下均同)。由图可见,当转速比绝对值逐渐增大而其他参量不变时,滞后区逐渐减小但不明显,跳跃幅度逐渐增大,并且升、降速过程中的跳跃点均向左移动,也即跳跃点的频率值均减小了,跳跃点的移动与临界转速的变化有关,从图中可见转速比的增大使系统的临界转速逐渐减小,滞后区减小并有向左移动,跳跃点也向左移动。
2.3中介轴承径向间隙对滞后特性的影响
当转速比λ=-1.2,阻尼比ξ=0.02,而中介轴承的径向间隙分别q0=1×10-6m,q0=5×10-6m,q0=10×10-6m时内转子的滞后特性如图6所示。由图可见,当中介轴承径向间隙增大时,滞后区逐渐增大,但升速跳跃幅度几乎不变,降速跳跃幅度却逐渐减小,而且升速跳跃的频率点几乎不动,降速跳跃的频率点却逐渐向左移动,这也说明了中介轴承径向间隙的变化对系统临界转速的影响比较微弱。
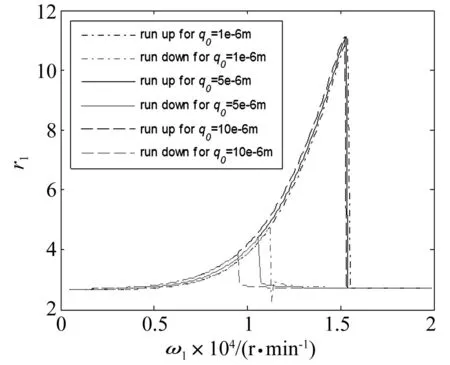
图6 径向间隙对滞后特性的影响 Fig.6 Radial clearance effects on hysteresis
2.4阻尼比对滞后特性的影响
当转速比λ=-1.2,径向间隙q0=5×10-6m,而阻尼比分别为ξ=0.01,ξ=0.02,ξ=0.05时内转子的滞后特性如图7所示。由图可见,阻尼比对滞后区的影响尤为明显,阻尼比的增大使滞后区逐渐减小,而且升速跳跃的幅度也逐渐减小,跳跃的频率点向左移动,也即升速跳跃发生时的频率值减小了。降速的跳跃幅度也有所减小,但减小的幅值不大,且降速跳跃的频率点也逐渐向左移动,这与系统临界转速的变化有关,从图中可见,阻尼比的增大使系统的临界转速减小,滞后区减小并有向左移动,跳跃点也向左移动。

图7 阻尼比对滞后特性的影响 Fig.7 Damping ratio effects on hysteresis
3结论
本文对一个考虑中介轴承非线性力的简化双转子模型的动力学方程进行了数值计算,发现该系统存在明显的滞后特性,而且相同参量条件下高、低压转子的滞后特性类似。进一步分别研究了转速比,中介轴承的径向间隙以及阻尼比对系统滞后特性的影响,得到如下结论:
(1)当转速比的绝对值逐渐增大而其他参量不变时,滞后区虽逐渐减小但变化不明显,而升、降速幅频曲线的跳跃幅度逐渐增大,并且由于转速比的增大使系统的临界转速逐渐减小,系统的滞后区向左移动,升、降速过程中跳跃发生的频率点也均向左移动。
(2)当中介轴承径向间隙增大时,系统的滞后区逐步增大,但升速幅频曲线的跳跃幅度几乎不变而降速的跳跃幅度逐步减小,而且降速跳跃的频率点逐渐向左移动,升速跳跃的频率点却几乎不动,这是由于径向间隙的增大对系统临界转速的影响较小所致。
(3)当阻尼比增大时,系统的滞后区逐渐减小,升速幅频曲线的跳跃幅度逐渐减小,降速的跳跃幅度也有所减小,但减小的幅值不大,并且由于阻尼比的增大使系统的临界转速减小,滞后区向左移动,升、降速过程中跳跃发生的频率点也均向左移动。
参考文献
[1]陈予恕,张华彪.航空发动机整机动力学研究进展与展望[J].航空学报,2011,32(8):1371-1391.
CHEN Yu-shu, ZHANG Hua-biao. Review and prospect on the research of dynamics of complete aero-engine systems[J].Acta Aeronautica et Astronautica Sinica,2011,32(8):1371-1391.
[2]Ferraris G, Lalanne M. Prediction of the dynamic behavior of non-symmetric coaxial co-or counter-rotating rotors [J]. Journal of Sound and Vibration,1996,195(4):649-666.
[3]Lalanne M, Ferraris G. Rotordynamics prediction in engineering [M]. England: Wiley,1989.
[4]Gupta K. Unbalance response of a dual rotor system: theory and experiment [J]. Journal of Vibration and Acoustics,1993,115:427-435.
[5]罗贵火,胡绚,杨喜关.反向旋转双转子系统非线性分析[J].振动工程学报,2009,22(3):268-273.
LUO Gui-huo, HU Xuan, YANG Xi-guan. Nonlinear Analysis of counter-rotating dual-rotor system[J]. Journal of Vibration Engineering,2009,22(3):268-273.
[6]胡绚.反向旋转双转子系统动力学特性研究[D].南京,南京航空航天大学,2007.
[7]罗贵火.反向旋转双转子系统振动特性分析与实验研究[D].南京:南京航空航天大学,1999.
[8]晏砺堂,王德友. 航空双转子发动机动静件碰摩振动特征研究[J]. 航空动力学报,1998,13(2):173-176.
YAN Li-tang, WANG De-you. Vibration features from rubbing between rotor and casing for a dual-shaft aeroengine[J]. Journal of Aerospace Power,1998,13(2):173-176.
[9]Hu Qing-hua, Deng Si-er, Teng Hong-fei. A 5-DOF model for aeroengine spindle dual-rotor system analysis[J]. Chinese Journal of Aeronautics, 2011,24,224-234.
[10]于海,陈予恕,曹庆杰. 多自由度裂纹转子系统非线性动力学特性分析[J]. 振动与冲击,2014,33(7):93-98.
YU Hai, CHEN Yu-shu, CAO Qing-jie. Nonlinear dynamic behavior analysis for a cracked multi-DOF rotor system[J]. Journal of Vibration and Shock, 2014,33(7):93-98.
[11]邓四二,付金辉,王燕霜,等. 航空发动机滚动轴承-双转子系统动态特性分析[J]. 航空动力学报,2013,28(1):195-204.
DENG Si-er, FU Jin-hui, WANG Yan-shuang, et al. Analysis on dynamic characteristics of aero-engine rolling bearing/dual-rotor system[J]. Journal of Aerospace Power, 2013,28(1):195-204.
[12]Liew A, Feng N, Hahn E J. Transient rotordynamic modeling of rolling element bearing systems[J].Journal of Engineering for Gas Turbines and Power,2002,124:984-991.
[13]闻邦椿,顾家柳,夏松波,等. 高等转子动力学[M]. 北京:机械工业出版社,2000.
[14]钟一鄂,何衍宗,王正,等.转子动力学[M].北京:清华大学出版社,1984.

第一作者李文峰男,博士生,1983年生
通信作者许爱强男,教授,博士生导师,1963年生
邮箱:253710081@qq.com

第一作者李小彭男,博士,教授,1976年生
