基于键合图的行星滚柱丝杠副动态特性建模与仿真

第一作者贺继鹏男，硕士生，1989年12月生

通信作者刘更男，博士，教授，博士生导师，1961年生

基于键合图的行星滚柱丝杠副动态特性建模与仿真

贺继鹏，刘更，马尚君，佟瑞庭

(西北工业大学陕西省机电传动与控制工程实验室，西安710072)

摘要：考虑行星滚柱丝杠副传动间隙、啮合面接触变形、丝杠扭转与拉压变形、加工误差、载荷分布、摩擦力及惯量等因素，运用键合图理论建立行星滚柱丝杠副动态特性分析模型，推导其状态方程。引入功率结型结构描述传动间隙引起的螺纹啮合面间接触力、阻尼力非线性分段特性，用LuGre模型反映啮合面摩擦力对行星滚柱丝杠副动态特性影响。以一组行星滚柱丝杠副参数为例，将其阶跃速度响应结果与Adams仿真结果进行对比，验证模型的正确性。分别研究丝杠转速、滑滚比对摩擦力响应特性影响及传动间隙、加工误差对刚度特性影响。分析结果有助于提高行星滚柱丝杠副动态精度及工作稳定性。

关键词：行星滚柱丝杠副；键合图；动态特性；动刚度

基金项目：国家自然科学基金资助项目(51275423)；教育部高等学校博士学科点专项科研基金(20126102110019)；中国博士后科学基金(2014M552483)；高等学校学科创新引智计划(B13044)

收稿日期：2014-07-16修改稿收到日期：2014-09-12

中图分类号:TH132.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.20.012

Abstract:Based on bond graph theory, a dynamic analysis model of planetary roller screw mechanism was presented, in which transmission clearances, contact deformations of threads, torsion and compression deformations of screw, machining errors, load distribution of threads, friction and inertias were taken into consideration. Meanwhile, the state equations of the model were derived. In the model, for describing the nonlinear and stepped properties of contact force and damping force caused by transmission clearances between thread surfaces, the concept of switched power junctions was introduced, and the influence of friction on dynamic characteristics of planetary roller screw mechanism was considered based on the LuGre model. Taking some planetary roller screw mechanism as an example, the calculated step response of velocity was compared with the result from Adams simulation to verify the effectiveness of the model. Then, the influences of rotating speed of screw and slide roll ratio on friction force response characteristics, and the influences of transmission clearances and machining errors on stiffness characteristics were investigated. The results can help to improve the dynamic accuracy and stability of planetary roller screw mechanisms.

Bond graph based dynamic characteristic modeling and simulation of planetary roller screw mechanism

HEJi-peng,LIUGeng,MAShang-jun,TONGRui-ting(Shaanxi Engineering Laboratory for Transmissions and Controls, Northwestern Polytechnical University, Xi’an 710072,China)

Key words:planetary roller screw mechanism; bond graph; dynamic characteristic; dynamic stiffness

行星滚柱丝杠副(Planetary Roller Screw Mechanism，PRSM)为可实现旋转运动与直线运动相互转化的传动机构。随航空、航天、武器装备及石油化工、机床、过程控制等对直线机电作动系统的更高要求，PRSM以其高精度、长寿命、大推力及高平稳性等优点成为直线机电作动系统重要执行机构[1-2]。

对PRSM的研究，Velinsky等[3]建立考虑滚滑运动的PRSM运动学分析模型，给出滚柱相对丝杠的滑动角、滑动速度计算方法。Hojjat等[4]对滚柱与丝杠接触侧进行受力分析，探究螺纹旋向对滚柱滚动、滑动趋势影响。Jones等[5]考虑滚柱节圆偏移建立PRSM运动学分析模型，研究各零件轴向偏移位移及滑动速度。Rys等[6]将滚柱等效为承受剪应力的立方体，借助有限元方法建立PRSM载荷分布计算模型。靳谦忠等[7]基于Hertz接触理论，推导材料弹性滞后及滚柱自旋滑动产生的摩擦力矩计算式；但文献大多致力于PRSM运动学、静力学及摩擦等研究，对动态特性研究较少。马尚君等[8]建立PRSM有限元模型，基于显示动力学有限算法对PRSM动态特性进行仿真分析，计算量较大，当模型参数改变或进行多能域联合仿真时通用性较差。而键合图理论则可进行系统动态特性分析，用其建立PRSM动态特性模型分析效率高，通用性强[9]。Karam等[10]在AMESim环境下建立反向式PRSM键合图模型，因主要分析机电作动系统性能，模型较简化，不能完全反映真实工作状态。因此，建立完整的PRSM键合图模型，进行动态特性分析及直线机电作动系统动态性能研究具有重要意义。

本文基于键合图理论，在LuGre摩擦力模型基础上综合考虑传动间隙、啮合面弹性变形、丝杠扭转及拉压变形、加工误差、载荷分布、滚滑摩擦及惯量，建立PRSM动态特性分析模型，通过与Adams仿真结果对比，验证本文模型的正确性；并对PRSM摩擦力响应、刚度特性进行仿真分析。

1PRSM基本运动关系

PRSM结构见图1，主要通过丝杠、滚柱与螺母螺纹啮合传递运动及动力，丝杠、滚柱及螺母牙型均为三角形，牙型角均90°。其中螺母仅沿轴向移动，不作周向转动，丝杠仅沿周向转动，不作轴向移动，滚柱除随螺母一起轴向移动外，亦绕丝杠轴线公转及绕自身轴线自转。

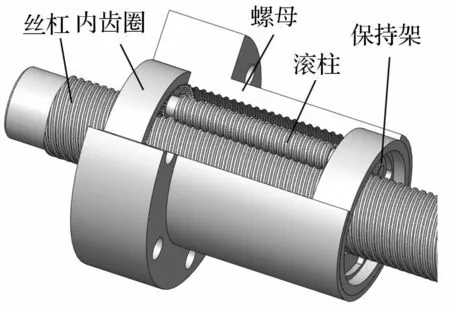
图1　PRSM结构图 Fig.1 The structure of PRSM

为保证PRSM螺母及滚柱侧不发生滑动，结构参数应满足以下条件[11]

(1)螺母、滚柱及丝杠直径满足

dN=dS+2dR

(1)

式中：dN，dR，dS分别为螺母、滚柱、丝杠在接触点处直径。

(2)设系数t=dS/dR，滚柱为单头螺纹时丝杠、螺母头数为

nS=nN=t+2

(2)

式中：nS为丝杠头数；nN为螺母头数。

(3)丝杠、滚柱及螺母旋向相同，均为右旋。

满足条件(1)、(2)、(3)时，各部件运动关系为

(3)

(4)

式中：ωR，ωe分别为滚柱自转、公转角速度；ωS为丝杠角速度。

螺母、滚柱轴向速度为

v=nspωS/(2π)

(5)

式中：p为滚柱螺距。

2啮合面间摩擦力键合图建模

2.1摩擦力模型

LuGre模型[12]不仅可描述两相互运动表面间静摩擦力、动摩擦力、粘性摩擦力，亦可描述Stribeck现象及stick-slip运动，为目前精密系统分析中应用较广的摩擦力分析模型[13]。用LuGre模型可更准确反映PRSM啮合面间摩擦特性。

LuGre模型中，摩擦力模型[14]可表示为

(6)

(7)

(8)

PRSM中除由滚柱自旋滑动产生的摩擦外，亦存在由材料弹性滞后产生的摩擦力，即

Frr=μrFn

(9)

式中：μr为滚动摩擦系数。

由于LuGre模型对不同摩擦力状态是连续的，且摩擦力为耗能元件，故用调质阻性元件(Modulated Resistive, MR)模拟PRSM中丝杠与滚柱、滚柱与螺母螺纹啮合面间摩擦力，调质信号为螺纹啮合面正压力。

2.2啮合面间相对滑动速度

PRSM工作过程中滚柱螺纹牙受力方向与丝杠轴线成一定夹角，导致滚柱自转、公转同时存在滑动。丝杠与滚柱啮合面间相对滑动速度为

vSR=-(rSωS+2rRωR)sin(θi)+

(rSωS+2rRωR)cos(θi)+rSωStan(λk)

(10)

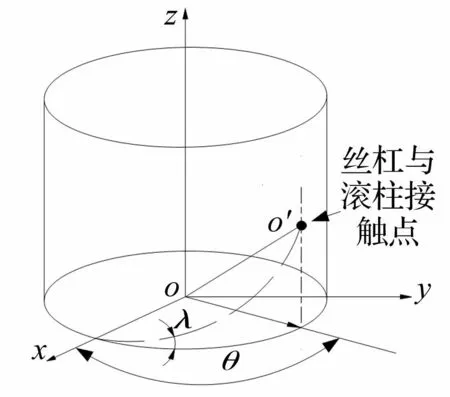
图2　PRSM固定坐标系 Fig.2 Ground coordinate of PRSM

式中：i，j，k分别为固定坐标系o-xyz三个单位向量，见图2；θ为丝杠与滚柱啮合点相对固定坐标系转角；rS，rR分别为丝杠、滚柱接触点半径；λ为丝杠螺旋升角；ωR为滚柱自转角速度；ωS为丝杠角速度。

设丝杠与滚柱接触状态在整个工作过程中不发生变化，由PRSM运动关系得

rSωS=-2rRωR

(11)

则丝杠与滚柱啮合面间相对滑动速度为

vSR=rSωStan(λk)

(12)

据丝杠与滚柱相对运动状态，将丝杠角速度分为滚柱滑动与滚动对应角速度两种形式，则滚柱滚动对应丝杠角速度为

(13)

将式(5)代入式(13)得滚柱滚动对应丝杠角速度与螺母直线运动速度关系为

(14)

此处用滑滚比定义滚柱滑动、滚动对应的丝杠角速度之比。

滚柱与螺母啮合时，为保证二者啮合良好，在二者两端分别装有外、内齿轮。滚柱在行星运动中其螺纹中径与齿节圆直径大小相等，且螺旋升角与螺母升角相等，故滚柱与螺母啮合时不会产生相对轴向位移及滑动。滚柱与螺母啮合面间相对滑动速度为

vRN=0

(15)

可见丝杠与滚柱啮合面间始终存在相对滑动，且仅存在轴向相对滑动速度，且与丝杠半径、转速及螺旋升角密切相关。滚柱与螺母在接触点处为纯滚动，啮合面间相对滑动速度为零。

建模时可用键合图中转换器(Transformer,TF)实现丝杠角速度与螺旋轨道啮合面间滑动速度转换。

2.3啮合面摩擦力键合图模型

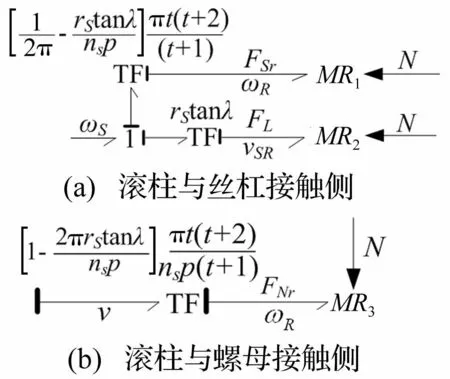
图3　PRSM啮合面摩擦力键合图模型 Fig.3 Bond graph model of PRSM friction

综合以上分析

可得滚柱与丝杠、螺母啮合面摩擦力键合图模型，见图3。其中FSr为丝杠侧滚动摩擦力，用MR1表示；FL为丝杠侧滑动摩擦力，用MR2表示；FNr为螺母侧滚动摩擦力，用MR3表示；N为啮合面作用力。

3考虑间隙及载荷分布的力特征键合图建模

据有限元分析知[15]，Hertz接触变形约占螺母相对丝杠轴向变形的98%，螺纹牙弯曲变形及滚柱轴向拉压变形占比较小。因此建模分析时忽略螺纹牙弯曲变形及滚柱拉压变形。

滚柱与丝杠或螺母啮合面间轴向接触力、接触变形关系为

(16)

式中：kj为滚柱与丝杠或螺母接触刚度；α为滚柱与丝杠或螺母接触角；λ为丝杠螺旋升角；K为轴向接触刚度；δj为啮合面轴向接触变形；下标j=s或n，s为滚柱与丝杠啮合面，n为滚柱与螺母啮合面。

单边传动间隙为b时，滚柱与丝杠或螺母轴向接触力为

(17)

式中：z为滚柱与丝杠或螺母啮合面相对轴向位移。

相对运动啮合面粘滞阻尼力可表示为

(18)

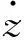
PRSM中螺纹加工误差σ可等效为间隙量，则单边传动间隙为b+σ。

由式(17)、(18)可见，考虑传动间隙及加工误差时，滚柱与丝杠或螺母啮合面间弹性力、阻尼力具有非线性分段特性。为表示该特性，引入功率结型结构[16]构建考虑传动间隙及加工误差时丝杠与滚柱单对螺纹牙啮合面间力特征键合图模型，见图4。

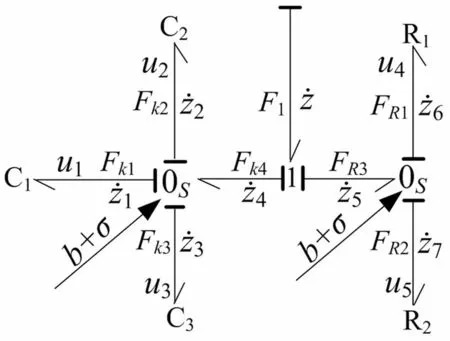
图4　考虑间隙、误差的啮 合面间力特征键合图模型 Fig.4 Bond graph model of force between threads considering clearances and errors

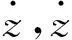
结合功率结型结构工作原理，得图4模型状态方程为

(19)

考虑PRSM载荷分布时，可据参与啮合螺纹牙数对键合图模型进行扩展，见图5。其中各参数上标1、i、n分别为参与啮合的第一对、第i对、第n对螺纹牙，n为螺纹牙数；F为螺纹牙间总作用力；其余符号同前。

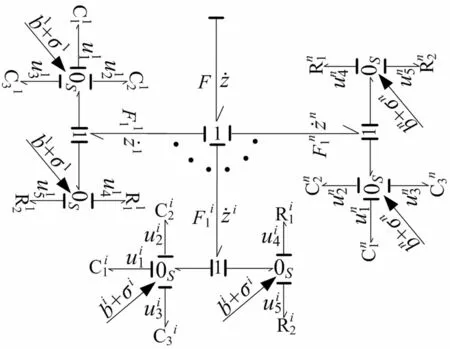
图5　考虑载荷分布的啮合面力特征键合图模型 Fig.5 Bond graphmodel of force between threads considering load distribution

图5模型状态方程为

(20)

滚柱与螺母啮合面的力特征键合图模型及状态方程分别与丝杠及滚柱相同。

4丝杠扭转及拉压特性

4.1丝杠扭转刚度

丝杠扭转变形与扭矩关系为

(21)

式中：TS为丝杠所受扭矩；G为材料剪切模量；φ为丝杠扭转角度；l为丝杠受扭转初始轴段长；dS为丝杠直径。

丝杠扭转刚度为

(22)

4.2丝杠拉压刚度

丝杠轴向拉压变形与载荷关系为

(23)

式中：FS为丝杠受轴向载荷；E为材料弹性模量；ε为丝杠拉压变形；l为丝杠受轴向载荷初始轴段长；dS为丝杠直径。

丝杠拉压刚度为

(24)

据丝杠扭转、拉压特性对PRSM工作影响，获得键合图模型，见图6。

图6　丝杠扭转与拉压特性键合图模型 Fig.6 Bond graphmodel of torsion and compression of screw

5PRSM键合图建模

5.1PRSM键合图模型

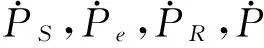
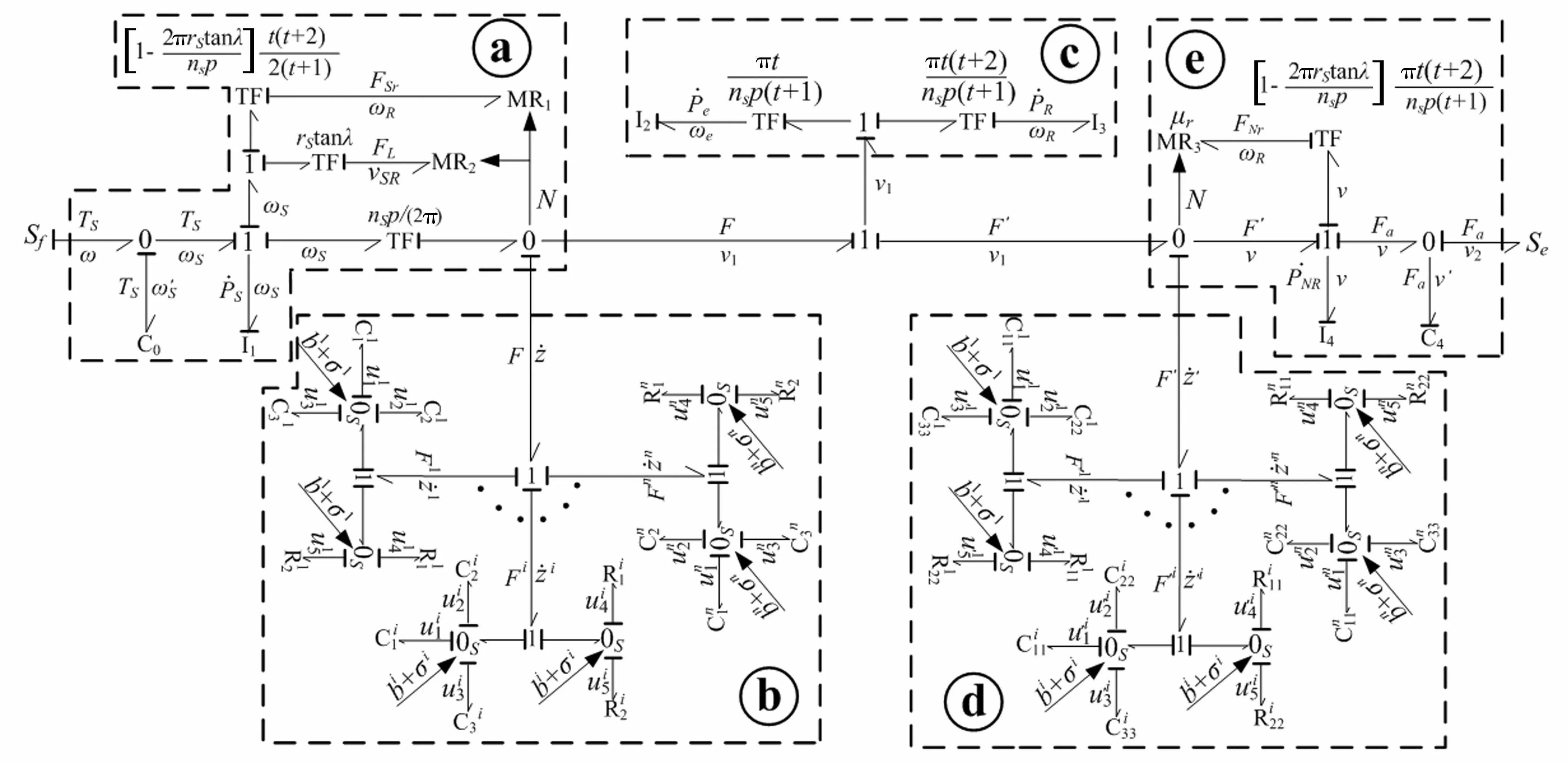
图7　PRSM键合图模型 Fig.7 Bond graph model of PRSM

据图7获得PRSM动态特性迭代计算方程为

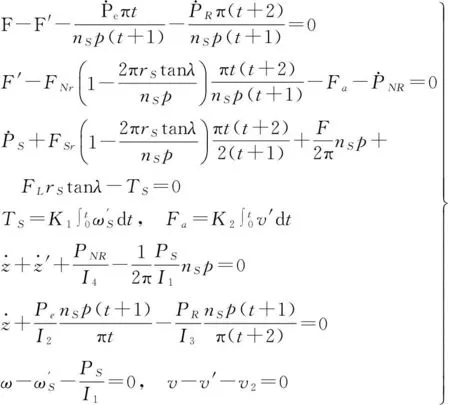
式中：F,F′分别为丝杠、螺母侧接触力，二者可由式(19)、(20)联立求解；PS=ωSI1；Pe=ωeI2；PR=ωRI3；PNR=vI4。

5.2模型验证

为验证模型的正确性，取PRSM结构参数见表1。在相同阶跃角速度输入下用20-sim软件对PRSM键合图模型(图7)输出速度进行仿真，并与Adams仿真结果对比，见图8。其中，Adams仿真为纯刚体模型，为与Adams仿真条件相同，分析PRSM键合图时忽略丝杠扭转及拉压刚度、PRSM传动间隙及加工误差影响。设丝杠输入角速度ω=62.8 rad/s，轴向负载Fa=16 000N。

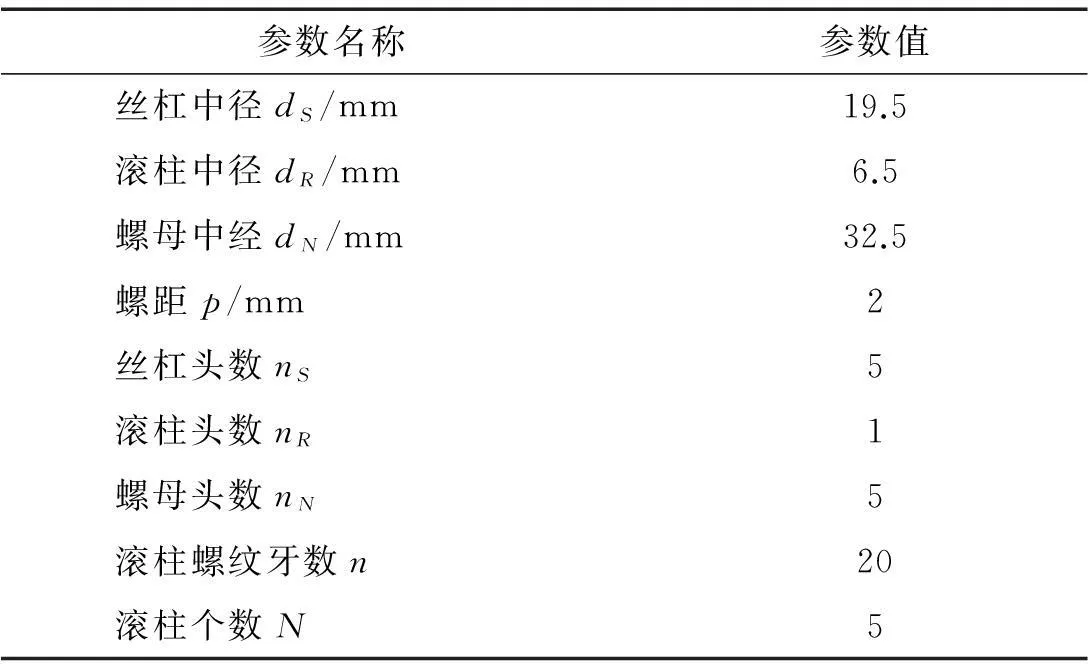
表1　PRSM结构参数

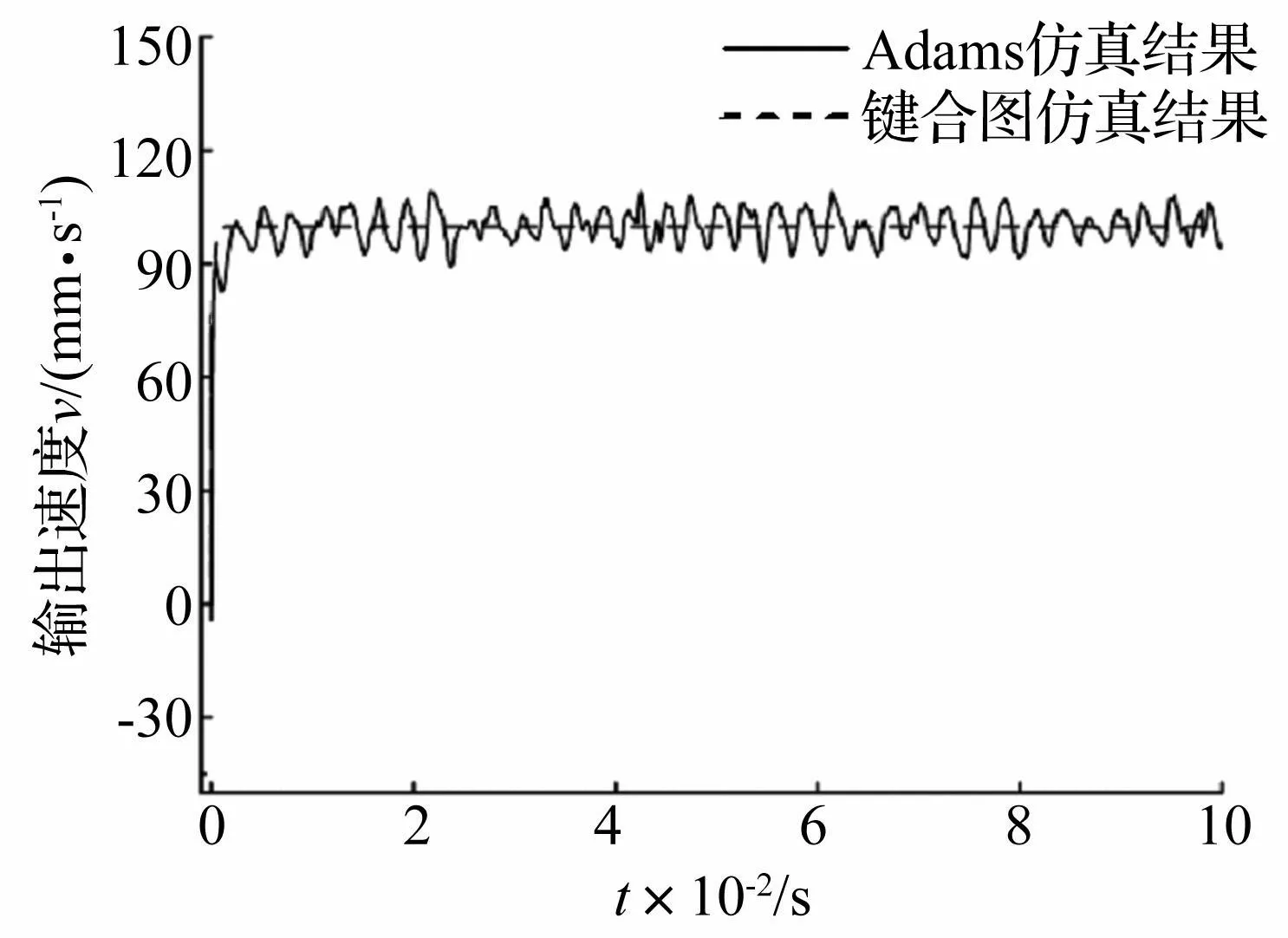
图8　螺母输出速度对比曲线 Fig.8 Comparison of nut speed response between Adams and bond graph

由图8看出，PRSM键合图模型与Adams模型速度响应曲线在上升阶段基本重合，达到稳定状态后键合图速度响应与Adams速度响应均值相对误差为0.5%，从而验证键合图模型的正确性。由于键合图模型考虑螺纹啮合面间接触变形，接触碰撞时阻尼作用较明显，而Adams模型为纯刚体模型，故键合图模型速度响应更平稳。

6基于键合图的动态特性仿真分析

6.1摩擦特性仿真及分析

主要研究丝杠输入角速度与滑滚比对摩擦力从0到最大值响应过程影响规律。由于加工误差对分析不同丝杠输入角速度或滑滚比下摩擦力响应变化规律影响较小，而加工误差会影响模型的收敛速度及精度，故分析中不考虑PRSM加工误差。用Runge-Kutta-Fehlberg求解器对图7模型进行求解。

6.1.1丝杠输入角速度对摩擦力响应影响

取PRSM单边传动间隙b=0.02 mm，轴向载荷Fa=1 600 N，计算获得不同丝杠阶跃角速度输入下摩擦力响应曲线见图9。由图9看出，在仿真起始短时间内摩擦力存在较大振荡，随丝杠输入角速度增加，摩擦力振荡程度增加，振幅明显增大，摩擦力响应速度显著提高，丝杠转速对摩擦力响应影响减小。丝杠输入角速度由12.5 rad/s增至37.68 rad/s时响应时间缩短约64%；继续增至62.8 rad/s时响应时间缩短约40%；达到稳定后摩擦力曲线重合。因在LuGre摩擦模型中摩擦系数是与相对运动速度相关的函数，速度越大摩擦系数趋于稳定值越快；丝杠输入角速度越大螺纹啮合面碰撞所需时间越短，接触力响应越快，从而提高摩擦力响应速度。

图9 不同丝杠输入角速度下摩擦力响应Fig.9Frictionresponseunderdifferentrotationspeedsofscrew图10 不同滑滚比下摩擦力响应Fig.10Frictionresponseunderdifferentslid-rollratios图11 不同传动间隙下动刚度特性Fig.11Dynamicstiffnessunderdifferentclearances

6.1.2滑滚比对摩擦力响应影响

保持传动间隙及轴向载荷不变，取丝杠输入角速度ω=62.8 rad/s，计算获得不同滑滚比下摩擦力响应曲线见图10。由图10看出，仿真起始短时间内摩擦力存在较大振荡，随滑滚比增加摩擦力振荡程度增加，振幅增大，但摩擦力响应速度增快，滑滚比对摩擦力响应影响减小。滑滚比由0.1增至0.3时响应时间缩短约60%，滑滚比由0.3增至0.5时响应时间缩短约25%。达稳定后摩擦力曲线重合。因滑滚比增大提高了整个运动过程中啮合面平均滑动速度，使LuGre摩擦模型中摩擦系数上升速度加快。

6.2刚度特性仿真与分析

6.2.1传动间隙对动刚度影响

为研究PRSM动刚度特性将丝杠输入端固定，即输入角速度ω=0 rad/s，在螺母上施加轴向谐波载荷Fa=16 000sin(2πft)N，f为载荷频率。设PRSM精度等级为IT5，螺纹公差带对称，加工误差服从正态分布，获得加工误差均值为0，标准方差Sd=0.44 μm。对不同单边传动间隙b，求得动刚度随载荷频率变化规律见图11。由图11看出，随传动间隙增大动刚度显著减小。因间隙会增大PRSM动态变形量，且载荷频率越高传动间隙对动刚度影响越大。对某固定传动间隙，动刚度曲线存在一个转折点，当载荷频率小于转折点对应频率时，随载荷频率增大动刚度逐渐增大；载荷频率大于转折点对应频率时动刚度略有下降。因当载荷频率增大到一定程度时传动间隙在总动态变形中占据主导地位，因此实际应用中应尽量避免PRSM工作在该频率区域。而传动间隙越小动刚度曲线转折点对应的频率越大。单边传动间隙由0.03减至0.02时动刚度曲线转折点对应频率增加16.7%，单边传动间隙由0.02减至0.01时动刚度曲线转折点对应频率增加35.7%。

6.2.2加工误差对动刚度影响

由于PRSM变形主要为螺纹牙Hertz接触变形，因此当载荷频率一定时，滚柱最大轴向接触变形反映PRSM动刚度。为研究加工误差对动刚度影响，分别计算考虑、不考虑加工误差两种情况下滚柱最大接触变形，分析两者比值与加工误差关系。

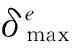
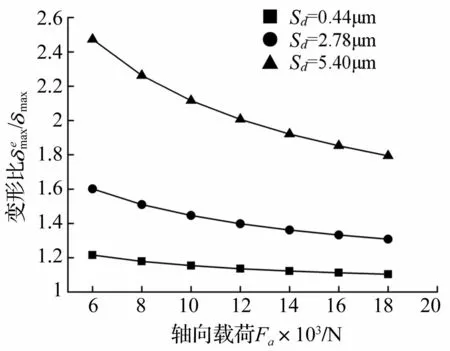
图12　滚柱最大接触变形与轴向载荷关系图 Fig.12 Relationship between contact deformations of roller and axial loads

7结论

据PRSM运动原理及受力特性，基于键合图理论，建立考虑传动间隙、加工误差、弹性变形及载荷分布等多因素的PRSM键合图模型，并将其速度响应结果与Adams模型仿真结果对比，验证本文模型的正确性。在此基础上对其摩擦特性、刚度特性进行仿真分析，结论如下：

(1)与现有PRSM动态特性分析方法相比，本文所建PRSM动态特性分析模型考虑因素较全面，建模方便，通用性强，可据系统具体要求对模型进行必要扩展与简化，且满足PRSM在多能域的联合仿真需求。

(2)随丝杠输入角速度增大摩擦力响应速度逐渐增大，丝杠输入角速度对摩擦力响应影响程度逐渐减小，达到稳定状态后摩擦力曲线重合。滑滚比对摩擦力响应影响趋势与丝杠输入角速度相同。

(3)载荷频率一定时动刚度随传动间隙增大而减小，载荷频率越高间隙对动刚度影响越大。对某一固定间隙动刚度曲线先增大后略有减小，即存在一个转折点，且间隙越小曲线转折点对应频率越大。

(4)考虑加工误差的动刚度较不考虑时小，且加工误差越大动刚度越小。轴向载荷越小加工误差对动刚度影响越显著。

参考文献

[1]Schinstock D E, Haskew T A. Dynamic load testing of roller screw EMA’S[J]. IEEE, 1996, 28(11):221-226.

[2]Tselishchev A S, Zharov I S. Elastic elements in roller-screw mechanisms[J]. Russian Engineering Research, 2008, 28(11): 1040-1043.

[3]Velinsky S A, Chu B, Lasky T A. Kinematics and efficiency analysis of the planetary roller screw mechanism[J]. Journal of Mechanical Design, 2009, 131(1):1-8.

[4]Hojjat Y, Agheli M M. A comprehensive study on capabilitiesand limitations of roller-screw with emphasis on slip tendency [J]. Mechanism and Machine Theory, 2009, 40(10):1887-1899.

[5]Jones M H, Velinsky S A. Kinematics of roller migration in the planetary roller screw mechanism[J]. 2012, 134: 1-6.

[6]Ryš J, Lisowski F. The computational model of the load distribution between elements in planetary roller screw[C]. 9th International Conference on Fracture & Strength of Solids, 2013:1-6.

[7]靳谦忠, 杨家军, 孙健利. 行星滚柱丝杠副的摩擦机理研究[J]. 华中科技大学学报, 1998, 20(6):82-84.

JIN Qian-zhong, YANG jia-jun, SUN Jian-li. The research on friction mechanism of the planetary roller screw[J]. Journal of Huazhong University of Science and Technology, 1998, 20(6): 82-84.

[8]马尚君,刘更,周建星,等. 行星滚柱丝杠副运转过程动态特性分析[J]. 振动与冲击, 2013, 32(3):167-171.

MA Shang-jun, LIU Geng, ZHOU Jian-xing, et al. Dynamic characteristic analysis of a planetary roller screw in operating process[J]. Journal of Vibration and Shock, 2013, 32(3): 167-171.

[9]唐进元,陈海峰,王祁波.考虑间隙和摩擦时的齿轮传动动力学键合图建模研究[J]. 机械工程学报, 2011, 47(9):53-59.

TANG Jin-yuan, CHEN Hai-feng, WANG Qi-bo. Dynamics model of gear transmission with combined friction and clearance by using bond graph method[J]. Journal of Mechanical Engineering, 2011, 47(9):53-59.

[10]Karam W, Mare J C. Modeling and simulation of mechanical transmission in roller-screw electro-mechanical actuators[J]. Aircraft Engineering and Aerospace Technology, 2009,81(4): 288-298.

[11]Ma Shang-jun, Liu Geng, Tong Rui-ting, et al. A new study on the parameter relationships of planetary roller screws[EB/OL]. Mathematical Problems in Engineering. http://dx.doi. 10.1155/2012/340437.

[12]Olsson H, Åström K J, deWit C C, et al. Friction models and friction compensation[J]. European Journal of Control, 1998, 4(3):176-195.

[13]Wang Xing-jian, Wang Shao-ping. High performance adaptive control of mechanical servo system with LuGre friction model: identification and compensation[J]. Journal of Dynamics Systems, Measurement and Control-Transactions of the ASME, 2012, 134(1):1-8.

[14]Åström K J, deWit C C. Revisiting the LuGre friction model [J]. IEEE Control Systems Magazine, 2008, 81(4):101-114.

[15]马尚君,刘更,佟瑞庭,等. 行星滚柱丝杠副轴向弹性变形的有限元分析[J]. 机械传动, 2012, 36(7):78-82.

MA Shang-jun, LIU Geng, TONG Rui-ting,et al. Finite element analysis of axial elastic deformation for planetary roller screw[J]. Journal of Mechanical Transmission, 2012, 36(7):78-82.

[16]Amod C U, Umanand L. Modeling of switching systems in bond graphs using the concept of switched power junctions[J]. Journal of the Franklin Institute, 2005, 342(2):131-147.

[17]刘占升,张敏,张光辉,等. 基于LuGre摩擦模型的叶片碰撞摩擦特性研究[J]. 振动与冲击, 2012, 31(12):172-178.

LIU Zhan-sheng, ZHANG Min, ZHANG Guang-hui, et al. Characteristics of impact-contact and friction between tips of blades based on LuGre model[J]. Journal of Virbration and Shock, 2012, 31(12):172-178.