一种适用于泄流结构振动分析的信号降噪方法

第一作者张建伟男，博士，副教授，1979年生

一种适用于泄流结构振动分析的信号降噪方法

张建伟，江琦，赵瑜，朱良欢，郭佳

(华北水利水电大学水利学院，郑州450011)

摘要：针对低信噪比泄流结构振动信号有效信息难以提取问题，提出将小波阈值与经验模态分解(EMD)联合的信号降噪方法。利用小波阈值滤除大部分高频白噪声，降低EMD端点效应；进行EMD分解获得具有相对真实物理意义的固态模量(IMF)；通过频谱分析重构特征信息IMF获得降噪信号。构造仿真信号，将该方法与数字滤波、小波分析及EMD降噪效果进行对比。结果表明，该方法能精确滤除泄流结构的振动噪声保留信号特征信息，滤波降噪较优越。将其用于拉西瓦拱坝水弹性模型，精确分析坝体结构振动优势频率，为坝体结构的安全运行与在线监测提供基础，亦为大型泄流结构在强背景噪声下的结构有效信息提取提供捷径。

关键词：泄流结构；振动信号；低信噪比；小波与EMD联合降噪；优势频率

基金项目：国家自然科学基金(51009066)；河南省高等学校青年骨干教师资助计划(2012GGJS-101)；河南省科技攻关(142102310122，142300410177，132102310320)资助

收稿日期：2014-10-28修改稿收到日期：2015-04-27

中图分类号:TV31; TB53

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.20.030

Abstract:In view of the difficulty in extracting useful characteristics from the vibration signal of flood discharge structure with low signal to noise ratio, a novel de-noising method, combining wavelet threshold and empirical mode decomposition (EMD), was proposed. First of all, a part of white noises were filtered out with the wavelet threshold method, which can reduce the endpoint effect of EMD; then the signal was decomposed with EMD, to obtain a series of intrinsic mode functions (IMFs) which contains real physical meanings; finally the IMFs including characteristic information were reconstructed to achieve the de-noised signal through spectrum analysis. Constructing a simulation signal, and comparing the filtering effect of this method with the conventional method of digital filter, wavelet threshold and EMD on the signal, it is shown that, the method presented is a superior de-noising method, which can filter the vibration noise of flood discharge structure accurately and retain the characteristic information. It has been used in the Laxiwa arch dam hydro-elastic model test, analyzing the dominate frequency of dam structure precisely, and providing the basis for safe operation and on-line monitoring of the dam structure.

De-noising method for vibration signal of flood discharge structure

ZHANGJian-wei,JIANGQi,ZHAOYu,ZHULiang-huan,GUOJia(College of Water Conservancy, North China University of Water Conservancy and Electric Power, Zhengzhou 450011, China)

Key words:flood discharge structure; vibration signal; low signal to noise ratio; combination of wavelet threshold and EMD; dominant frequency

流体诱发的结构振动极其复杂，为二者相互作用现象。泄流结构的动力特性[1-2]为判断其运行状态、健康程度及振动危害的重要指标。泄流结构振动信号在获取、输送过程中会受环境激励的高频白噪声及低频水流脉冲噪声等不同程度干扰，从而影响结构健康状况及振动危害评价精度。为获取结构振动信号的优势特征信息，须采取有效的信号处理方法。因此，振动信号降噪精确度成为关键。

振动信号降噪分析时，傅里叶变换[3-4]作为最基本方法通过频域分析刻画信号的频率特性，但不提供任何时域信息，只能单纯解决周期性信号或平稳信号降噪问题。数字滤波[5]的时域方法通过对信号离散数据进行差分方程数学运算达到滤波目的。该方法需确定一些技术指标(如通带截止频率、阻带截止频率、通带波动系数等)，利用数学、数字信号处理原理由滤波器模型逼近给定指标。该方法的不足在于信号滤波效果与指标的确定关系密切，且有固定数量延时。小波阈值降噪[6]利用变换阈值对含噪信号进行处理，除去或减少噪声影响；并对处理后系数进行小波重构获得较好的真实信号估计。该方法最大缺点是小波基、阈值计算及阈值函数的选择准则问题[7-8]，不同选择准则可能造成不同滤波效果。EMD分解[9]突破信号处理“先验”缺陷，非常适合非线性、非平稳信号。该方法据信号自身尺度特性自适应分解成含不同瞬时频率的IMF，每个IMF具有一定物理意义，且能简化信号处理过程。对泄流振动信号，由于强背景噪声干扰，构造IMF各极值点在整个采样空间分布不均匀，且局部噪声干扰信号频率与结构特征信号频率相近，会出现不同程度的端点效应及混频问题[10-11]，导致EMD分解出现偏离。

基于以上研究，本文提出基于小波阈值与EMD分解联合的滤波方法。其中小波阈值分离信号中的高频白噪声为EMD做铺垫，而EMD可进一步分离白噪声及低频水流噪声，从而能提高滤波精度。将其用于泄流结构，可为分析结构振动优势频率及坝体结构安全运行与在线监测奠定基础。

1信号降噪基本原理

1.1小波阈值消噪

小波阈值降噪的基本原理即小波分解后白噪声仍为白噪声，分布广，幅值小；而有用信号则被压缩到少量小波系数中，幅值较大。据该性质设计门限值，视小于此门限值的小波系数为噪声小波系数，全部置零；大于此门限值的小波系数为有用信号，且保留，从而除去或减少噪声影响。处理后系数通过小波重构获得较好的真实信号估计。两种阈值处理方法[12]为

硬阈值函数

(1)

软阈值函数

(2)

Donoho给出的阈值求解公式为

(3)

式中：σ为噪声方差；N为信号数据长度。

1.2经验模态分解(EMD )

EMD分解实现过程：对任意原始信号x(t)找到信号所有极大、极小值点；分别用三次样条函数对所有极值点插值，拟合成原始信号的上、下包络线xmax(t)及xmin(t)；上下包络线所围区域含所有信号数据，获得均值m1(t)；用原始信号减去均值m1(t)，得到新的信号h1(t)，即

h1(t)=x(t)-m1(t)

(4)

若h1(t)满足IMF分量的两个条件，则称h1(t)为第一个固态模量；若h1(t)不满足IMF分量的特点，则将h1(t)作为原始信号。重复以上步骤直至获得满足IMF分量特征的第k次数据h1k(t)，即

h1k(t)=h1(k-1)(t)-m1(k-1)(t)

(5)

为避免出现循环次数过多的分解，h1k(t)不仅满足IMF分量的两个特点，亦应满足筛分终止准则，方能获得满足要求的IMF分量。引入终止准则

(6)

通常，Sd值越小固有模态分量的线性及稳定性越好。研究表明，Sd取0.2～0.3时既可保证固态模量的稳定性，也能使IMF具有相应的物理意义。h1k(t)满足要求时则称其为第一阶IMF分量，记为c1(t)，原始信号x(t)减去c1(t)为剩余信号，即残差r1(t)为

r1(t)=x(t)-c1(t)

(7)

将r1(t)作为新信号重复以上分解过程，获得满足要求的c2(t)，从而获得残差r2(t)，按以上分解方法循环计算每个IMF，直至残差为单调函数时分解终止。信号x(t)可表示为

(8)

2小波阈值与EMD联合降噪的提出

2.1小波阈值与EMD联合滤波思想

泄流结构振动信号为含高频白噪声及低频水流的非平稳非线性信号。小波阈值降噪对白噪声抑制能力较强，通过阈值处理能滤除高频白噪声；但由于泄流振动信号大部分属于低信噪比信号，真实信号常淹没于噪声中。为保证滤波精度，需对小波阈值处理后信号进一步处理。EMD实质即将信号依自身时间尺度特征自适应分解成从高频到低频的IMF，突破传统信号处理方法瓶颈，无需先验知识选择相应技术指标或函数，极大降低人为误差。基于EMD分解特点，对小波阈值处理后信号进行EMD分解。因实际信号处理中的强噪声，EMD分解信号两端点不能确定极值，使样条插值时产生数据拟合误差，上下包络线在端点附近发生扭曲。

因此，利用本文所提小波阈值与EMD联合降噪方法，据有效信息及噪声在小波分解尺度、EMD分解空间的不同规律，进行有效信噪分离。该方法本质在于对有效信息表现出传递特性，对噪声表现出抑制特性。

2.2小波阈值与EMD联合滤波流程图

为直观表述信号处理过程，建立小波阈值与EMD联合降噪流程，见图1。处理过程中6个核心问题为：

(1)确定小波分解层数。白噪声作为随机过程由一系列离散数据组成。据离散数据自相关特性，利用白化检验[13]通过判断各层小波系数是否具有白噪声特性可自适应确定分解层数。设离散数据dk(k=1,2,…,N)自相关序列为ρ(i)(i=1,2,…,M)，若ρ(i)满足式(9)则认为dk为白噪声序列，M通常取5～10。

(9)

实际振动测试信号中，由于白噪声中含弱相关信号，无法确定有用信号的弱相关信号或噪声产生的随机信号，因此先对小波系数经去相关处理再进行白化检验。将信号进行小波分解，对高频系数去相关分析后进行阈值处理，将高频系数中相关信号分离，对重构的高频信号进行白化检验。若非白噪声分解结束，若为白噪声进行下一步分解，直至获得非白噪声序列。

图1　小波阈值与EMD联合滤波降噪方法流程 Fig.1 The flow chart ofcombined wavelet threshold and EMD de-noising method

(2)计算各层小波系数阈值。Donoho提出的阈值计算公式适用于高信噪比信号，对被噪声淹没的低信噪比泄流结构振动信号，因保留太多较大噪声小波系数而影响降噪效果；且噪声小波系数随分解层数增加不断降低，但该阈值公式计算全局阈值，显然不合理，因此对阈值公式进行改进，即

(10)

式中：σ为噪声方差；N为信号数据长度；j为分解层数；e≈2.718 28为底数。

(3)选合适的阈值函数。通常用软、硬阈值函数，但硬阈值函数不连续，出现伪吉布斯现象；软阈值函数虽连续，但处理后小波系数存在偏差。因此需改进阈值函数。

(4)对重构信号进行EMD分解。EMD分解提取非平稳信号的瞬时频率及幅值，自适应分解获得从高频到低频的IMF。由于小波阈值先滤掉大部分高频奇异点，减少EMD分解层数，降低端点极值拟合误差及混频效应，使各IMF分量能正确反映信号真实物理意义。

(5)对各IMF进行频谱分析。提取反映真实信号物理特征的有用IMF，利用时空滤波器重构信号，得到精确降噪后信号。

(6)对降噪效果进行评定。引入信噪比 (SNR)及根均方误差(RMSE)作为降噪效果评定标准[14]。

信噪比为

(11)

根均方误差为

(12)

3仿真分析

3.1构造模拟信号

为检验本文方法降噪性能，构造泄流结构振动模拟信号x(t)，函数表达式为

x(t)=10e-tπ/2sin(15t)+5e-t/3sin(20t)

叠加低频噪声、高频白噪声后信号函数为

x1(t)=8e-t/3sin(3t)+x(t)+3randn(m)

式中：t为时间；采样频率100 Hz，采样时间10 s；randn(m)为均值为零、标准差为1的标准正态分布白噪声，m为样本个数。

设振动幅值单位为微米(μm)，x(t)、x1(t)时程曲线及功率谱密度见图2、图3。

图2　信号x(t)时程曲线与功率谱密度 Fig.2 Time history curve and power spectral density curve of signal x(t)

图3　信号x 1(t)时程曲线与功率谱密度 Fig.3 Time history curve and power spectral density curve of signal x 1(t)

3.2仿真对比

由图3可知，信号所含强噪声淹没了真实信号部分优势频率。分别用数字滤波、小波分析、EMD、小波阈值与EMD联合降噪方法进行降噪分析，计算4种方法处理后SNR及RMSE指标，见表1，降噪前后信号时程线对比见图4，用小波阈值与EMD联合方法降噪，信号前后功率谱密度对比见图5。

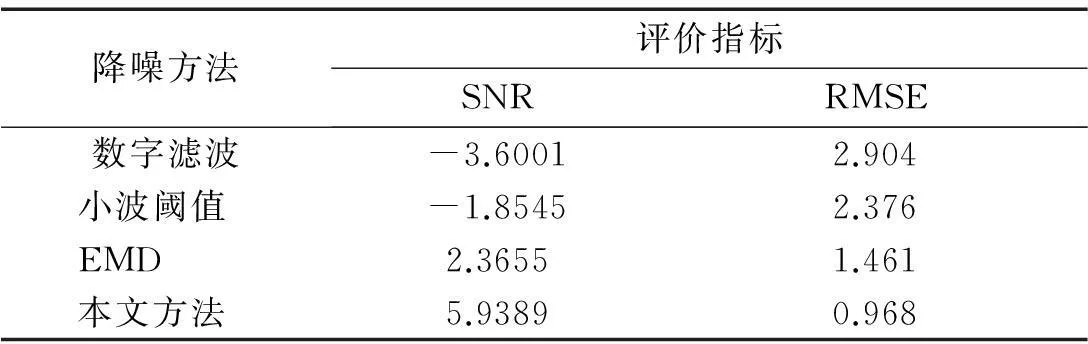
表1　四种方法降噪效果评定指标对比

图4　x 1(t)四种方法滤波降噪效果对比 Fig.4 Comparison of four filter methods for signal x 1(t)

图5　x 1(t)小波阈值与EMD联合降噪功率谱密度曲线 Fig.5 Power spectral density curve after combined wavelet threshold and EMD of signal x 1(t)

3.3结果分析

由表1、图4可知，本文方法降噪后信噪比最大，根均方误差较小，降噪前后时程线拟合最佳，说明噪声已基本消除。由图5功率谱密度曲线对比再次证实本方法能有效滤除噪声，保留振动信号特征优势频率。由此表明小波阈值与EMD联合降噪能有效滤除低信噪比信号噪声，适合泄流结构振动信号降噪。

4工程实例

以拉西瓦拱坝为工程背景，建立比尺1∶100的水弹性模型，材料为加重橡胶，模型坝高2.5 m，水弹性模型见图6。为反映拱坝振动情况，在坝顶布置11个动位移响应测点，考虑拱坝振动以径向为主，切向、垂直振动相对较小，本文仅研究径向振动(R方向)，测点布置见图7。在测点布置DP型地震式低频振动传感器(DSP-0.35-20-V)，该传感器具有抗震、耐冲击、高稳定度及良好的低频输出特点，且可测量μm级振动位移，适合高拱坝位移测量。测试工况为表深孔联合泄洪，此时上游水位高程2 457.0 m，采样频率100 Hz，采样时间40 s。

图6 拉西瓦水弹性模型Fig.6Hydro-elasticmodelofLaxiwa图7 测点布置示意图Fig.7Arrangementofdobservepoints

对坝顶振动响应最大测点0#采集的数据进行分析。原始信号时程及功率谱密度曲线见图8。由图看出，原始信号振动能量主要集中在10 Hz以下的低频部分，属于典型的受迫振动响应。响应中背景分量占绝对比重，结构振动信息被低频水流噪声及高频环境噪声淹没。

图8 0测点时程与功率谱密度曲线图Fig.8Timehistorycurveandpowerspectraldensitycurveofmeasuredpoint0# 图9 z(t)特征图与0测点信号特征图比较Fig.9Comparisonbetweenz(t)andoriginalsignalatpoint0# 图10 滤波后时程及功率谱密度曲线 Fig.10Timehistorycurveandpowerspectraldensitycurveafterdenoise

据图1算法流程，用本文方法对测点信息滤波分析。利用小波阈值滤除部分高频白噪声，据仿真信号特性选db5小波，分解层数为4层，分解重构后获得滤除白噪声信号；进行EMD分解，自适应分解获得从高频到低频的9个IMF分量，记为c1～c9，分析每个IMF频谱可知c2～c9主频主要集中在10 Hz以下。叠加c1～c9信息后获得信号z(t)，与原始信号0#测点时程及功率谱密度曲线对比见图9。由图9看出，z(t)信息主要集中在低频，为由水流脉冲荷载引起的干扰信息，应滤除；由时空滤波器重构含特征信息的IMF，获得滤除高频白噪声、低频水流噪声信号y(t)。

滤除全部噪声后信号y(t)时程及功率谱密度曲线见图10。由图10看出，滤波后信号在9.9 Hz、18.6 Hz、20.4 Hz、29.6 Hz、31.4 Hz处存在明显峰值，特征峰值与文献[5]模态参数辨识结果一致。

5结论

(1)本文所提小波阈值与EMD联合滤波降噪方法方法适用于泄流结构振动响应分析。不仅能克服小波阈值处理中盲目选择参数、对低信噪比信号降噪能力不足等缺点，亦能有效抑制EMD分解端点效应及混频问题，提高滤波降噪精度。

(2)本文方法对低信噪比的振动信号降噪具有优越性。通过对拉西瓦拱坝泄流振动分析，能精确提取坝体结构振动信息，分析结构振动优势频率，为坝体结构安全运行及在线监测奠定基础，同时亦为解决大型泄流结构在强背景噪声下有效信息提取提供捷径。

参考文献

[1]张建伟,康迎宾,张翌娜,等. 基于泄流响应的高拱坝模态参数辨识与动态监测[J]. 振动与冲击, 2010, 29(9):146-150.

ZHANG Jian-wei, KANG Ying-bin, ZHANG Yi-na, et al. Modal parameter identification and dynamic monitoring of high arch dam under vibration response induced by flow discharge[J]. Journal ofVibration and Shock, 2010, 29(9): 146-150.

[2]练继建,张建伟,李火坤,等. 泄洪激励下高拱坝模态参数识别研究[J]. 振动与冲击, 2007, 26(12):101-105.

LIAN Ji-jian, ZHANG Jian-wei, LI Huo-kun, et al. Study on modal parameter identification of high arch dam under flood discharge excitation[J]. Journal ofVibration and Shock, 2007, 26(12):101-105.

[3]Igor D, Jubisa S L, Marko S. Robust time-frequency representation based on the signal normalization and concentration measures[J].Signal Processing, 2014(104): 423-431.

[4]胡晓依,何庆复,王华胜,等. 基于STFT的振动信号解调方法及其在轴承故障检测中的应用[J].振动与冲击,2008, 27(2): 82-86.

HU Xiao-yi, HE Qing-fu, WANG Hua-sheng, et al. Vibration signal demodulation method based on STFT and its application in rolling bearing fault detections[J]. Journal of Vibration and Shock, 2008,27(2):82-86.

[5]张建伟.基于泄流激励的水工结构动力学反问题研究[D].天津:天津大学,2008.

[6]Dohono D L, Johnstone I M. Ideal spatial adaptation by wavelet shrinkage[J]. Biometrika, 1994, 81(3):425-455.

[7]唐进元,陈维涛,陈思雨,等.一种新的小波阈值函数及其在振动信号去噪分析中的应用[J].振动与冲击, 2009, 28(7): 118-121.

TANG Jin-yuan, CHEN Wei-tao,CHEN Si-yu, et al. Wavelet-based vibration signal denoising with a new adaptive thresholding function [J]. Journal of Vibration and Shock, 2009, 28(7):118-121.

[8]Mallat S. A theory formultire solution signal decomposition: the wavelet representation[J]. IEEE Trans on PAMI, 1989, 11(7):674-693.

[9]Huang N E, Shen Z，Long S R,et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London, Series A:Mathematical, Physical and Engineering Sciences,1998,454(3):903-995.

[10]白春华,周宣赤,林大超,等.消除EMD端点效应的PSO-SVM方法研究[J].系统工程理论与实践,2013,33(5): 1298-1306.

BAI Chun-hua, ZHOU Xuan-chi, LIN Da-chao, et al. PSO-SVM method based on elimination of end effects in EMD[J].Systems Engineering-theory andPractice, 2013, 33(5):1298-1306.

[11]薛年喜. Matlab在数字信号处理中的应用(2版)[M].北京:清华大学出版社,2008.

[12]Donoho D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory,1995,41(3):613-627.

[13]张吉先, 钟秋海, 戴亚平.小波门限消噪法应用中分解层数及阈值的确定[J]. 中国电机工程学报, 2004, 24(2): 118-122.

ZHANG Ji-xian, ZHONG Qiu-hai, DAI Ya-ping. The determination of the threshold and the decomposition order in threshold de-noising method based on wavelet thrasform [J]. Proceedings of the CSEE, 2004, 24(2): 118-122.

[14]钟建军,宋健,由长喜,等.基于信噪比评价的阈值优选小波去噪法[J]. 清华大学学报:自然科学版,2014,54(2): 259-263.

ZHONG Jian-jun, SONG Jian, YOU Chang-xi, et al. Wavelet de-noising method with threshold selection rules based on SNR evaluations[J]. Journal of Tsinghua University: Science and Technology,2014,54(2):259-263.