C2⊗C4中无偏的最大纠缠基的构造

*通信作者： 南华(1972—)，女，博士，副教授，研究方向为应用泛函分析.

C2⊗C4中无偏的最大纠缠基的构造

王天娇,南华*

( 延边大学理学院 数学系， 吉林 延吉 133002 )

摘要：在两体空间C2⊗C4上利用Pauli矩阵研究了最大纠缠基的具体形式，并给出了在C2⊗C4系统中构造无偏基的方法以及充要条件.另外,利用一个特殊的过渡矩阵A，构造出了5组彼此无偏的最大纠缠基.

关键词：最大纠缠基； 无偏基； Pauli矩阵； 过渡矩阵

收稿日期：2015-03-24

文章编号：1004-4353(2015)02-0132-04

中图分类号：O177.3

Construction of mutually unbiased maximally entangled bases in quantum system C2⊗C4

WANG Tianjiao，NAN Hua*

(DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China)

Abstract：Using the Pauli matrices, the explicit construction of maximally entangled bases in the bipartite quantum system C2⊗C4 is studied in this paper. A method of constructing mutually unbiased maximally entangled bases in C2⊗C4 is provided, and the necessary and sufficient conditions are given. Moreover, utilizing a special unitary matrix A， we construct five maximally entangled bases which are mutually unbiased each other.

Key words： maximally entangled bases; mutually unbiased bases; Pauli matrices; transition matrix

已知空间Cd中MUB的最大数目N(d)不超过d+1，且当空间维数d是素数幂时,N(d)=d+1[2].文献[3-4]研究了单体2到6维空间上的无偏基个数，对于空间维数d是非素数幂的合数时,N(d)还不确定，即使是对最小的素数6.近来，人们发现只有在具有最大数目的无偏测量基的系统中Mean King问题才能得到解决，而且最大数目的无偏测量基在量子纠错过程中也具有重要作用[5]，基于量子无偏基的重要应用，人们对其纠缠性质进行了研究[6-7].量子纠缠作为一种重要的物理资源，在量子力学基础和量子信息中起着重要的作用，并在量子传输、量子纠错、超密编码等方面都有重要应用，其中最大纠缠态在量子信息处理中尤为重要[8].

在多体量子系统中MUB问题变得更加复杂,MUB既可以是直积基、最大纠缠基，也可以是不可扩展的直积基和不可扩展的最大纠缠基等[9-10].文献[9]给出了在三体量子系统C2⊗C2⊗C2中无偏基的构造方法；文献[10-11]在C2⊗C3空间中研究了由不可扩展的最大纠缠基构造两组无偏基的一般方法;文献[12]在C3⊗C4空间中给出了由不可扩展的最大纠缠基构成的两组无偏基.基于以上研究，本文研究两体空间C2⊗C4中最大纠缠基的具体形式，以及在C2⊗C4系统中构造无偏基需要满足的充要条件.

1C2⊗C4中的最大纠缠态

(1)

其中σi(i=1,2,3)是Pauli矩阵,σ0=I2是2×2的单位矩阵.可以验证式(1)中的8个态矢都是最大纠缠的,同时两两正交.事实上，8个态矢:

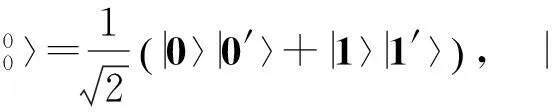
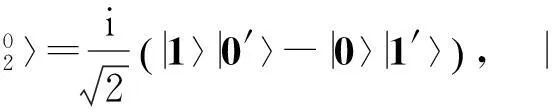
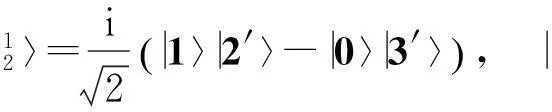
构成C2⊗C4中的一组最大纠缠基.

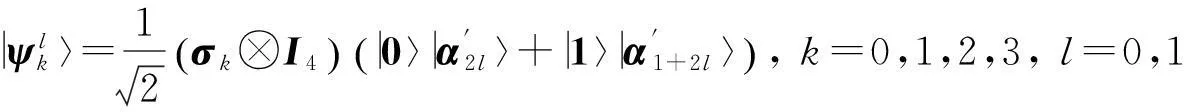
(2)

2C2⊗C4中无偏的最大纠缠基的构造

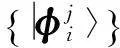
(3)

命题1最大纠缠基(1)和(2)彼此无偏的充要条件是

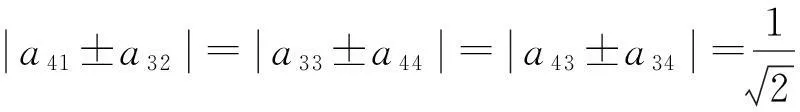
(4)

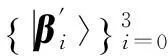
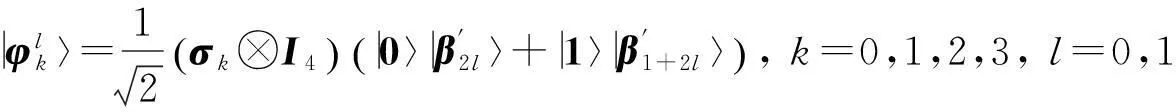
(5)

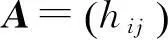
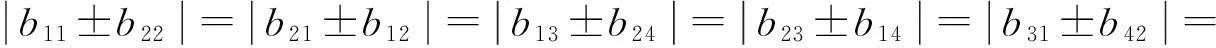
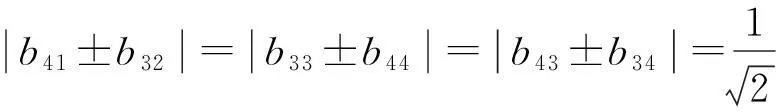
(6)

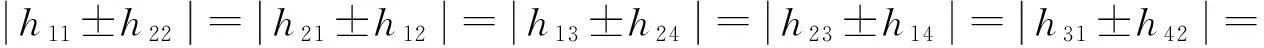
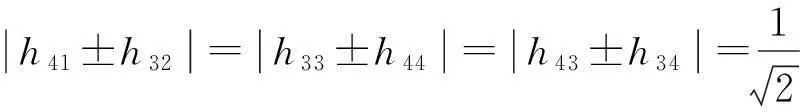
(7)

由以上得到如下的结论：

命题2在空间C2⊗C4中3组最大纠缠基(1)、(2)和(5)两两无偏的充分必要条件是过渡矩阵A和B满足式(4)、(6)和式(7).

构造尽可能多的无偏基在量子信息中具有重要意义.在C2⊗C4空间中构造无偏基的关键就是找到能够满足条件(4)、(6)和条件(7)的过渡矩阵.尽管在理论上给出了构造无偏基的方法和需要满足的条件，但实际构造无偏基却非易事.本文找到了一个特殊的过渡矩阵：

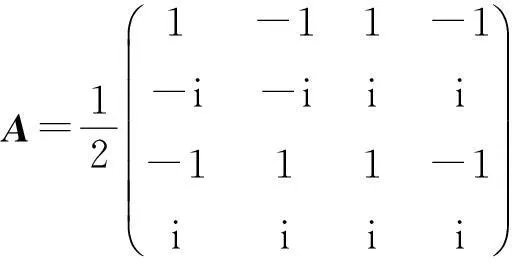
(8)

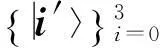
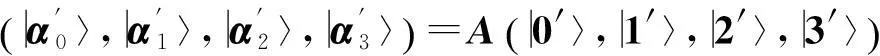
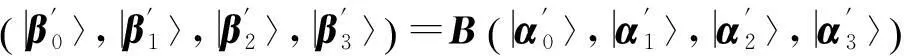
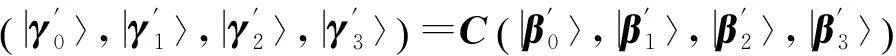
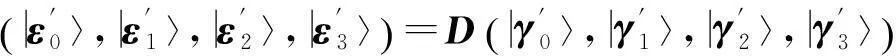
(9)

其中B=A， C=A2， D=A4.由以上5组标准正交基可以构造出C2⊗C4中5组最大纠缠基：

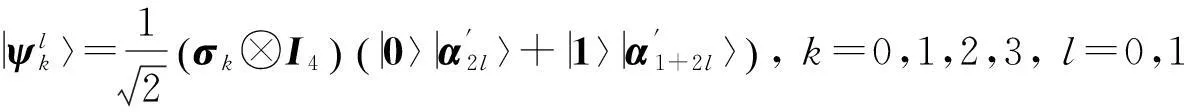
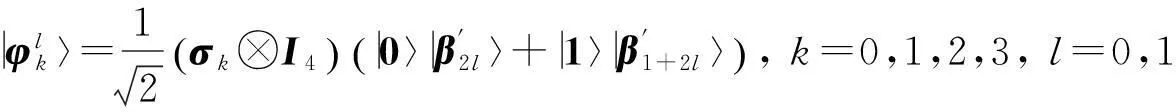
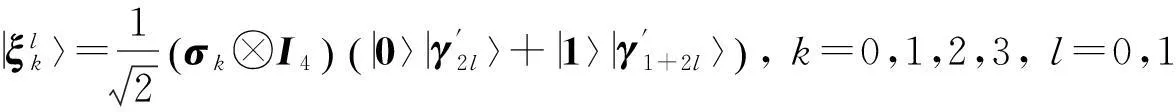
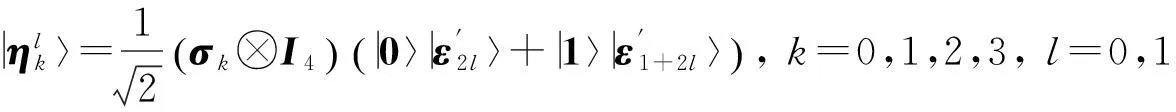
通过计算验证表明这5组基底是两两无偏的.

注1对于任意两体空间这样的酉矩阵A未必一定存在，但对某个过渡矩阵A进行适当的行或列变换，也应该可以类似地得到其他的过渡矩阵B，C等.

参考文献：

[1]WoottersWK,FieldsBD.Optimalstate-determinationbymutuallyunbiasedmeasurements[J].AnnPhys(NY), 1989,191(2):363-381.

[2]AdamsonDBA,SteinbergAM.Improvingquantumstateestimationwithmutuallyunbiasedbases[J].PhysRevLett, 2010,105:030406.

[3]BrierleyS,WeigertS,BengtssonI.Allmutuallyunbiasedbasesindimensiontwotofive[J].QuantumInformComput, 2010,10:803-820.

[4]McnultyD,WeigertS.Thelimitedroleofmutuallyunbiasedproductbasesindimension6[J].JPhysA:MathTheor, 2012,45(10):102001.

[5]BennettCH,WiesnerSJ.Communicationviaone-andtwo-particleoperatorsonEinstein-Podolsky-Posenstates[J].PhysRevLett, 1992,69:2881-2884.

[6]KlimovAB，SychD，Sanchez-SotoLL，etal.MutuallyunbiasedbasesandgeneralizedBellstates[J].PhysRevA, 2009,79：052101.

[7]雷丽霞，王天娇，南华.C2⊗C6中的最大纠缠基与无偏基[J].延边大学学报:自然科学版,2014，40(4)：311-313.

[8]Caruso F, Bechmann-Pasquinucci H, Macchiavello C. Robustness of a quantum key distribution with two and three mutually unbiased bases[J]. Phys Rev A, 2005,72：032340.

[9]Ghiu Iulia. Generation of all sets of mutually unbiased bases for three-qubit systems[J]. Phys Scr, 2013,T153：014027.

[10]杨强,陶元红,张军,等.C2⊗C3中无偏的不可扩展的最大纠缠基[J].哈尔滨理工大学学报，2014,19(4)：84-87.

[11]Nizamidin H, Ma T, Fei S M. A note on mutually unbiased unextendible maximally entangled bases in C2⊗C3[J]. Int J Theor Phys, 2015,54：326-333.

[12]Nan H, Tao Y H, Li L S, et al. Unextendible maximally entangled bases and mutually unbiased bases in Cd⊗Cd′[J]. Int J Theor Phys, 2015,54：927-932.

[13]Li Z G, Zhao M J, Fei S M, et al. Mixed maximally entangled states[J]. Quant Inf Comput, 2012,12(1/2):63-73.