一个最佳值为对数的Hilbert型积分不等式
2016-01-12巫伟亮
一个最佳值为对数的Hilbert型积分不等式
巫伟亮
( 嘉应学院 数学学院, 广东 梅州 514015 )
摘要:运用参量化思想、估算权函数方法及实分析技巧,建立了一个新的核为(λ>0,δ∈{1,-1})的Hilbert型积分不等式及其等价形式,并证明了它们的常数因子为最佳值,同时得到了该不等式的一些应用.
关键词:Hilbert型积分不等式; 权函数; 等价式; 最佳值
收稿日期:2015-02-26
基金项目:广东省自然科学基金博士启动项目(S2013040015141);嘉应学院科研重点项目(2012KJZ02)
文章编号:1004-4353(2015)02-0129-03
中图分类号:O178
A Hilbert-type integral inequality with the best value as logarithm
WU Weiliang
(SchoolofMathematics,JiayingUniversity,Meizhou514015,China)

Key words: Hilbert-type integral inequality; weight coefficient; equivalent form; the best value
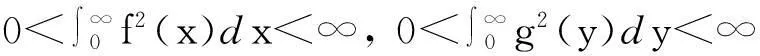
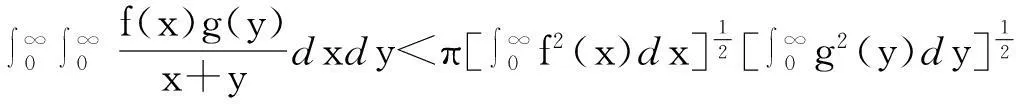
(1)
其中常数因子π都是最佳值.近年来,杨必成等对含齐次及非齐次核进行了研究,并对不等式(1)进行了推广和改进[3-6].2012年,巫伟亮[7]得到了一个含多参数的Hilbet型积分不等式:

(2)
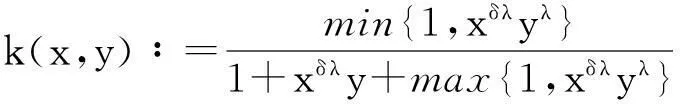
的Hilbert积分不等式及其等价形式,并证明了它们的常数因子是最佳值.
1引理及其证明
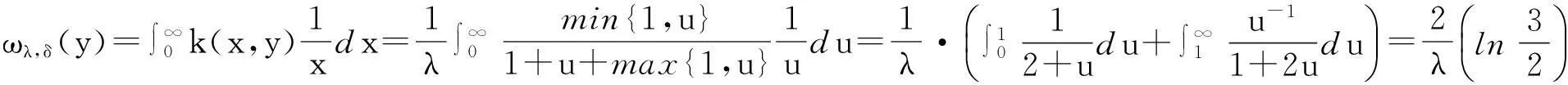

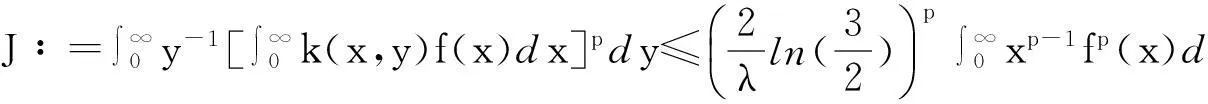
(4)
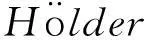
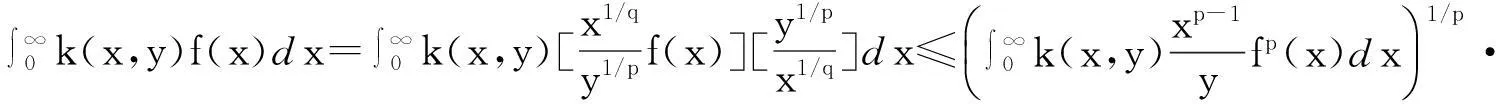

(5)
根据引理1的计算结果,应用交换积分变换的Fubini定理[9],有
故式(4)成立.证毕.
2主要结果及其证明
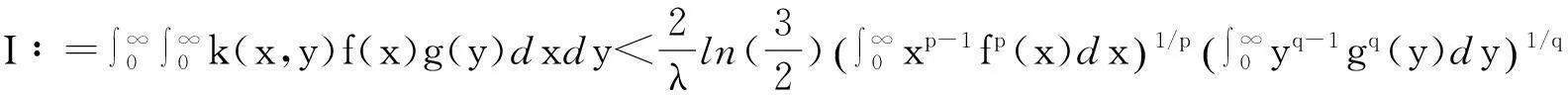
(6)

(7)
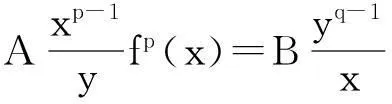
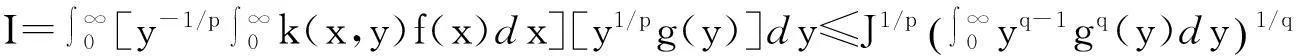
(8)
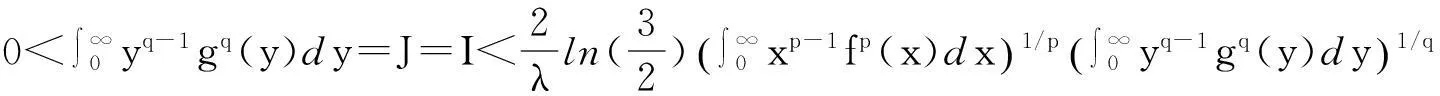
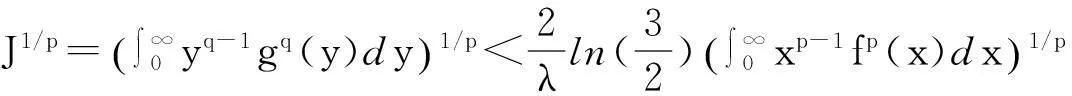
(9)
将式(9)两边p次方,可得式(7),且它与式(6)等价,证毕.
证明任意给定ε>0, Eδ∶={x>0;xδ≤1},设
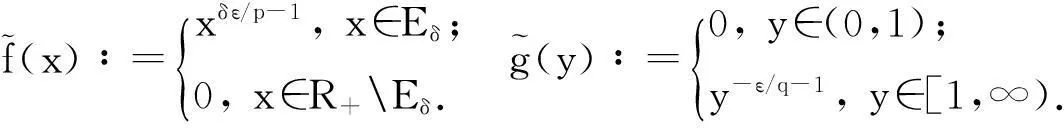
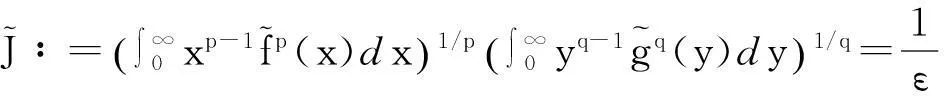
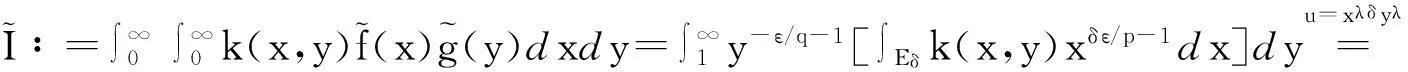


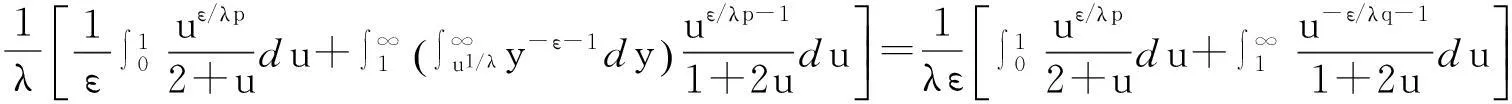
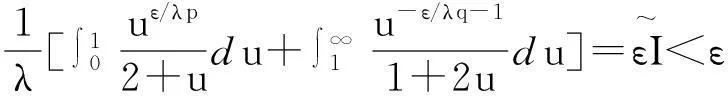
(10)
由Fatou引理[9]、式(10)及极限的保号性,得
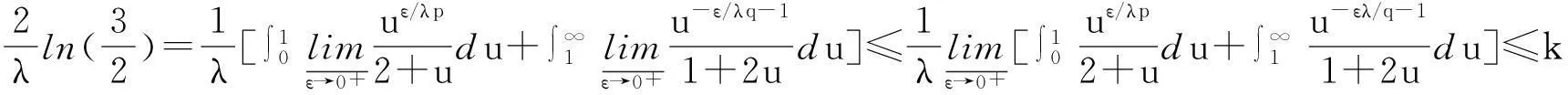

注1在式(6)中,取δ=-1, p=q=2, λ=1,得式(2),可见式(6)是式(2)的最佳推广.
注2在式(6)、(7)中,取δ=1, p=q=2, λ=1,可得到一个新的具有最佳常数因子的非齐次核Hilbert型积分不等式及其等价形式:
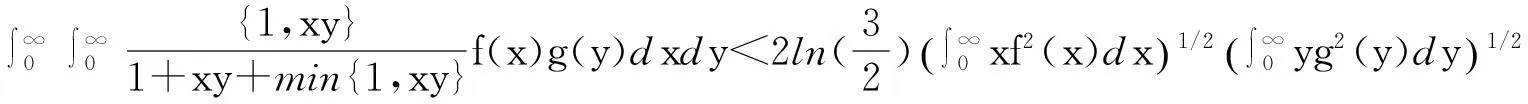
(11)
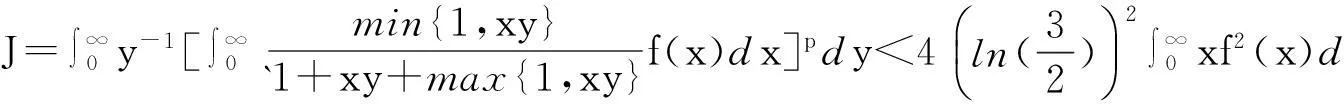
(12)
参考文献:
[1]Hardy G H, Littlewood J E, Polya G. Inequalities[M]. Cambridge: Cambridge University Press, 1952:255-292.
[2]Mintrinovice D S, Pecaric J E, Fink A M. Inequalities Involving Functions and Their Integrals and Derivatives[M]. Boston: Kluwer Academic Publishers, 1991:187-215.
[3]杨必成.参量化的Hilbet型不等式研究综述[J].数学进展,2009,38(3):257-268.
[4]杨必成.一个零齐次核的Hilbert型积分不等式[J].山东大学学报:理学版,2010,45(2):103-106.
[5]刘琼.一个多参数的Hilbert型积分不等式[J].吉林大学学报:理学版,2009,47(5):903-908.
[6]巫伟亮.一个最佳常数为Beta函数的Hilbert型积分不等式[J].延边大学学报:自然科学版,2014,40(2):100-103.
[7]巫伟亮.一个含多参数的Hilbert型积分不等式[J].广西师范学院学报:自然科学版,2012,29(2):34-36.
[8]匡继昌.常用不等式[M].济南:山东科技出版社,2004:3-29.
[9]匡继昌.实分析引论[M].长沙:湖南教育出版社,1996:118-122.
