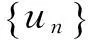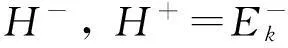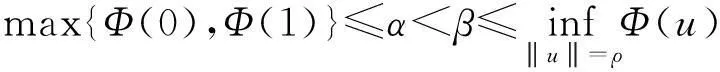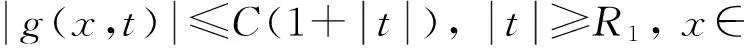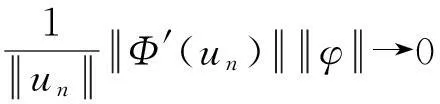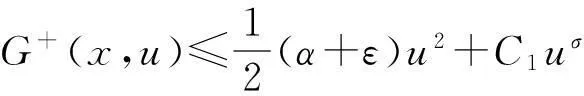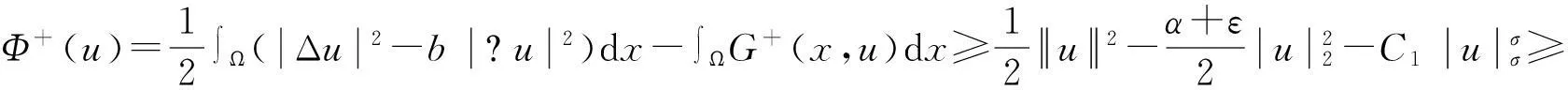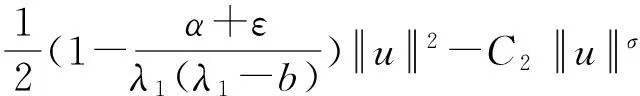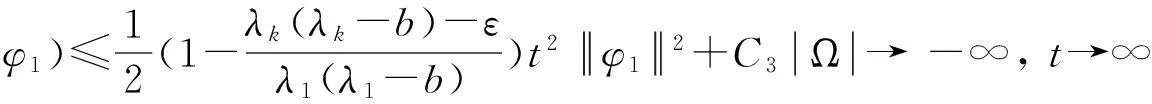四阶椭圆方程非平凡解的多重性
2016-01-12刘春晗,王建国
四阶椭圆方程非平凡解的多重性
刘春晗,王建国
( 齐鲁师范学院 数学学院, 山东 济南 250013 )
摘要:在非共振的情况下讨论了一类不满足Ambrosetti-Rabinowitz型增长条件的四阶椭圆方程.首先,证明泛函Φ满足(PS)条件.其次,证明泛函Φ满足山路引理的其他条件.最后,利用Morse理论和山路引理获得了方程的3个非平凡解.
关键词:山路引理; 临界群; 非平凡解
收稿日期:2014-05-12
基金项目:国家自然科学基金资助项目(10971179);山东省高等学校科技计划项目(J12L153);齐鲁师范学院青年教师科研基金资助项目(2014L1001)
文章编号:1004-4353(2015)02-0111-05
中图分类号:O175.25
Multiplicity of nontrivial solutions for fourth-order elliptic equations
LIU Chunhan,WANG Jianguo
(SchoolofMathematics,QiluNormalUniversity,Jinan250013,China)
Abstract:The fourth-order elliptic equations at no resonance are discussed without assuming Ambrosetti-Rabinowitz type growth conditions. Firstly, we prove that the functional Φ satisfies (PS) condition. Secondly, we prove that the functional Φ satisfies the other conditions of Mountain Pass Lemma. Finally, three nontrivial solutions are obtained by using Morse Theory and Mountain Pass Lemma.
Key words: Mountain Pass Lemma; critical group; nontrivial solution
0引言
本文考虑方程
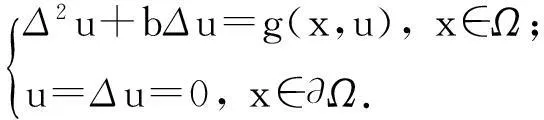
(1)

为后续讨论需要,首先给出如下假设条件:
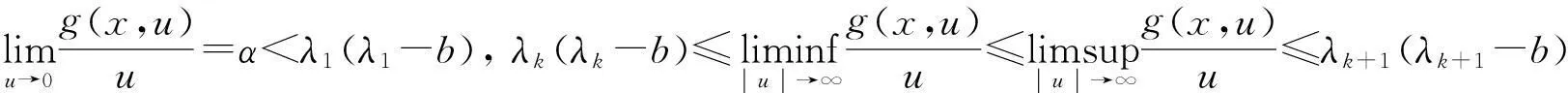
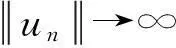
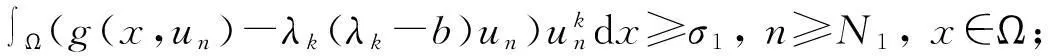
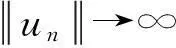
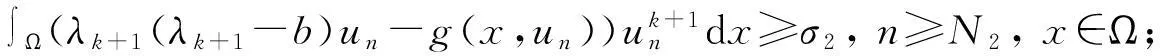
(H4)g(x,0)=0,∀x∈Ω.
注1容易看出条件(H1)要弱于文献[2]中的条件(H2).
首先考虑特征值问题

(2)
记λk(k∈N)与φk(k∈N)分别是特征值问题(2)的特征值及相应的特征函数,且满足0<λ1≤λ2≤λ3≤…≤λk→ +∞,第一特征向量φ1>0,对x∈Ω.下面考虑特征值问题
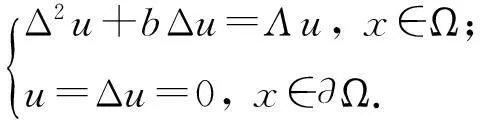
(3)
易得出λk(λk-b)(k∈N)以及特征向量φk(k∈N)满足特征值问题(3),即λk(λk-b)是问题(3)的特征值.
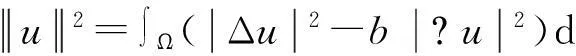
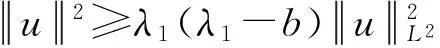
(4)
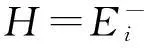
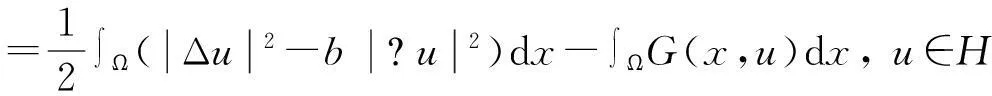
引入下面的截断问题:
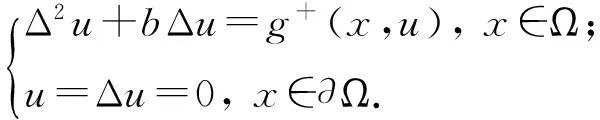
(5)
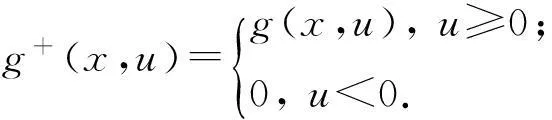
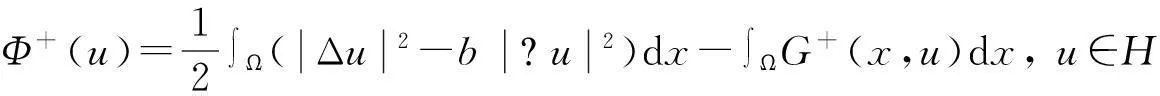
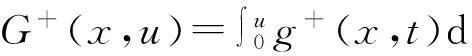
类似地,可以定义
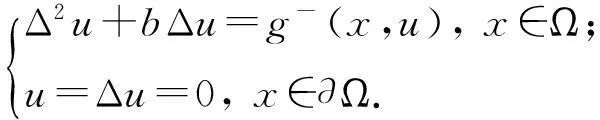
(6)

以下给出临界群和Morse理论的相关知识[3-4].
设H是Hilbert空间,泛函Φ(u)∈C2(H,R)满足(PS)条件或(C)条件,用Hq(H,Y)表示具有整系数的q阶奇异相对同调群.设ν0是Φ的孤立临界点,且Φ(ν0)=c∈R.记Φc={ν∈H|Φ(ν)≤c},K={ν∈H|Φ′(ν)=θ}.称群Cq(Φ,ν)=Hq(Φc,Φc{ν0}),q∈Z为Φ在ν0处的q阶临界群.若设K是有限集,称Cq(Φ,∞)=Hq(H,Φc),q∈Z为Φ在无穷远点处的临界群,其中c 引理1的证明过程类似于文献[5]中Lemma3.2的证明,故略.同理可得: 引理3的证明过程类似于文献[6]中Lemma2.5的证明,故略. 注2在定理1中,若把条件换成Φ满足(C)条件,结论依然成立. 1主要结果及其证明 定理3如果g(x,u)满足假设条件(H1)—(H4),且b<λ1,则方程(1)至少存在3个非平凡解. (7) wn⇀w于H,wn→w于L2(Ω),wn→wa.e.x∈Ω. (8) 由(H1)可知,存在常数C及R1使得 (9) 由式(7)可得,对任意的φ∈H,有 (10) ∫Ω(ΔwΔφ-bwφ)dx=∫Ωr(x)wφdx, (11) 因此w∈H是方程Δ2w+bΔw=rw的弱解. cμ(Φ,∞)0,μ=dimH+. (12) 另外,由于α<λ1(λ1-b),θ是Φ的局部最小值点,所以 cq(Φ,0)=δq0Z. (13) 由式(12)和(13)可知,Φ有非平凡临界点u1满足 cμ(Φ,u1)0. (14) Cq(Φ,u2)≅δq1Z. (15) 类似地,可以证明Φ-(u)满足定理1的所有条件,从而获得Φ的另一个负的临界点u3,且满足 Cq(Φ,u3)=δq1Z. (16) 最后,由式(14)—(16)和μ≥k>2,知u1,u2,u3是方程(1)的3个不同的非平凡解. 参考文献: [1]PeiRC.Nontrivialsolutionsforafourth-ordersemilinearellipticproblem[J].MathematicaApplicata, 2013,26(1):190-197. [2]WeiYH.Multiplicityresultsforfourth-orderellipticequations[J].JMathAnalAppl, 2012,385:797-807. [4]LiangZP,SuJB.Multiplesolutionsforsemilinearellipticboundaryvalueproblemswithdoubleresonance[J].JMathAnalAppl, 2009,354:147-158. [5]SuJB.Semilinearellipticboundaryvalueproblemswithdoubleresonancebetweentwoconsecutiveeigenvalues[J].NonlinearAnal, 2002,48:881-895. [6]MarinoB,EnricoS.SemilinearEllipticEquationsforBeginners[M].London:Springer-Verlag, 2011. [7]BartschT,LiSJ.Criticalpointtheoremforasymptoticallyquadraticfunctionalsandapplicationstoproblemswithresonance[J].NonlinearAnalTMA, 1997,28:419-441. [8]RobinsonS,SteveB.Multiplesolutionsforsemilinearellipticboundaryvalueproblemsatresonance[J].ElecJDiffEqu, 1995,1995:1-14.