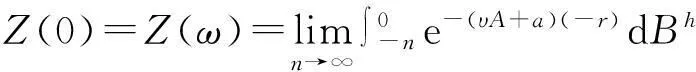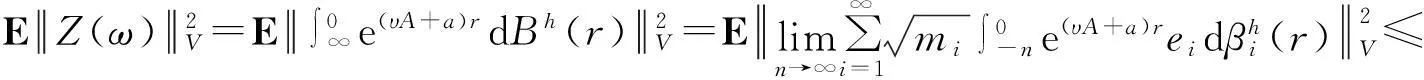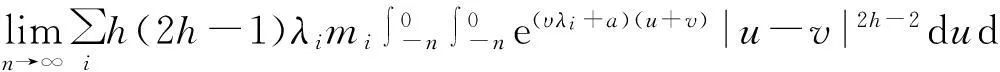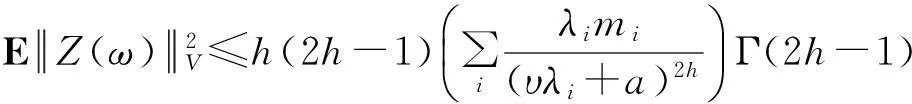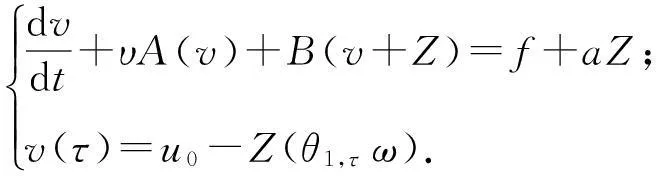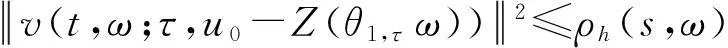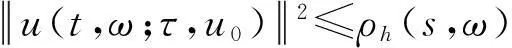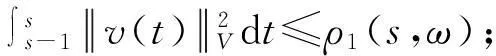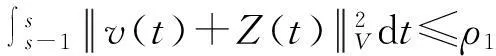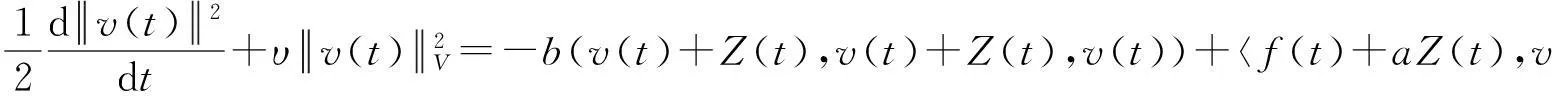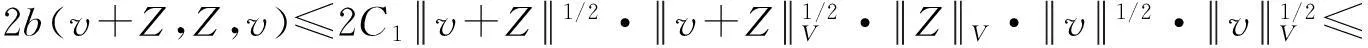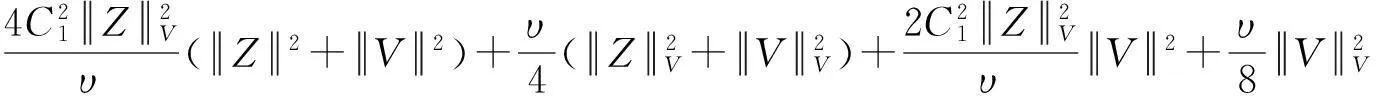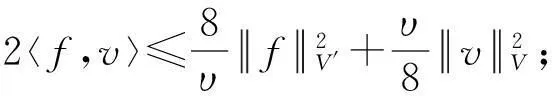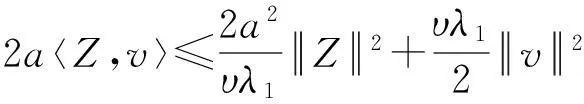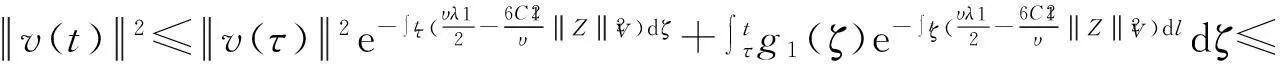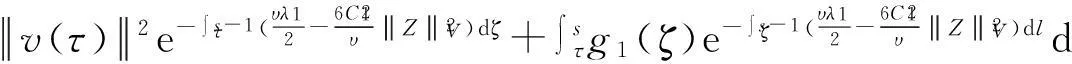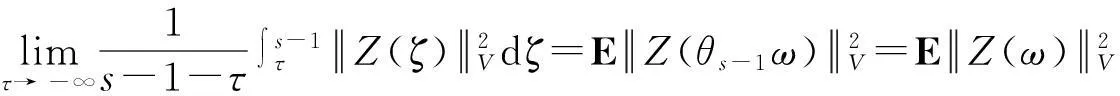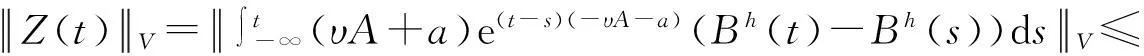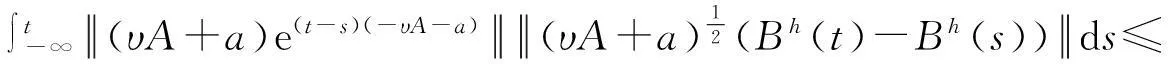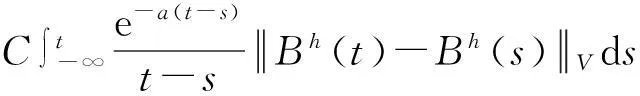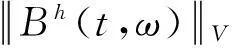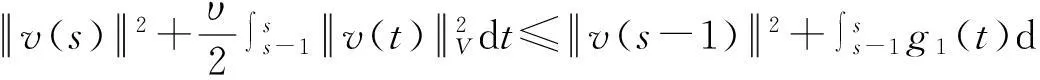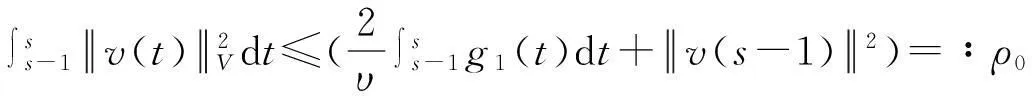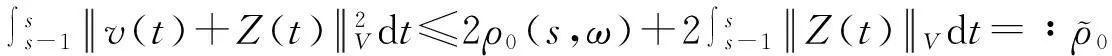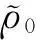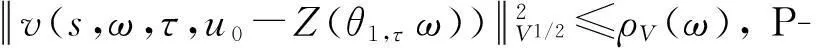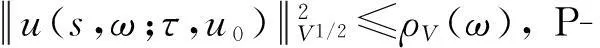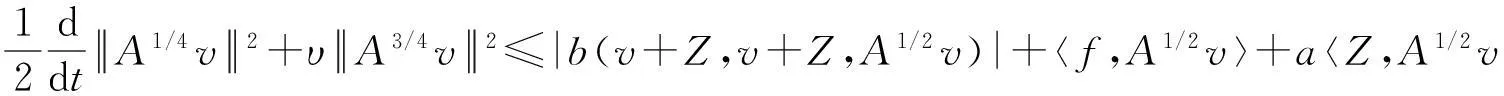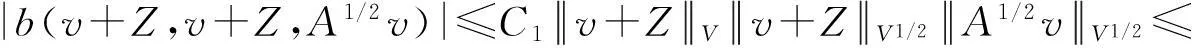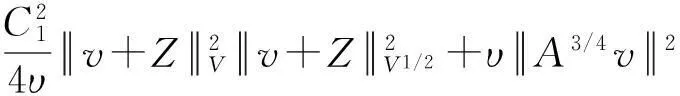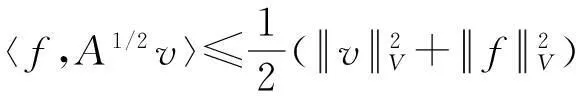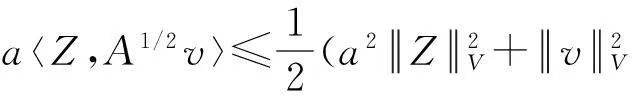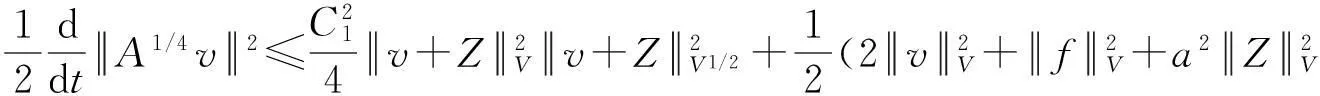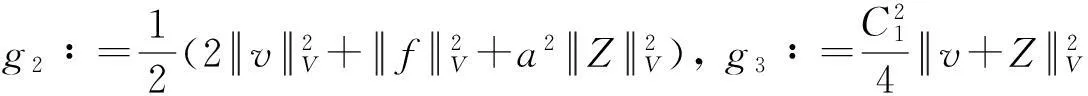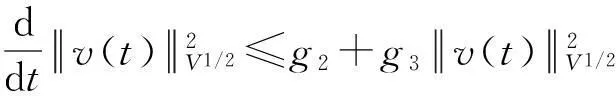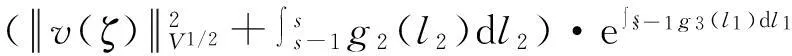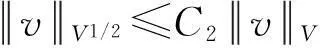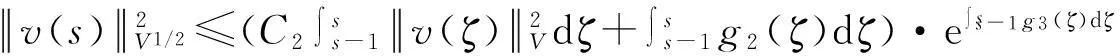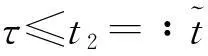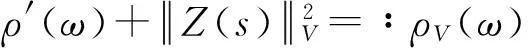分形布朗运动驱动的Navier-Stokes方程的渐近行为

通信作者： 韩英豪(1963—)，男,理学博士，副教授,研究方向为无穷维动力系统.

分形布朗运动驱动的Navier-Stokes方程的渐近行为

韩英豪，张磊,杨永芳,胡晓雪

( 辽宁师范大学 数学学院, 辽宁 大连 116029 )

摘要：在具有光滑边界∂O的有界区域O∈R2上考虑了如下由Hurst参数为,1)的分形布朗运动驱动的非自治Navier-Stokes方程的长时间动力行为

在适当的条件下,应用先验估计方法证明了由上述方程生成的随机动力系统的随机吸引子的存在性.

关键词：分形布朗运动; 随机拉回吸引子; Navier-Stokes方程

收稿日期：2015-05-28

文章编号：1004-4353(2015)02-0095-08

中图分类号：O211.63; O175.29

The asymptotic behavior of the Navier-Stokes equation driven by fractional Brownian motion

HAN Yinghao,ZHANG Lei,YANG Yongfang,HU Xiaoxue

(SchoolofMathematics,LiaoningNormalUniversity,Dalian116029,China)

Key words： fractional Brownian motion; random pullback attraction; Navier-Stokes equation

0引言

设O为在R2上具有光滑边界∂O的有界区域,本文在O上研究如下不可压缩流体的由分形布朗运动驱动的非自治Navier-Stokes方程

(1)

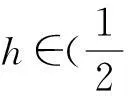
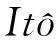
1预备知识

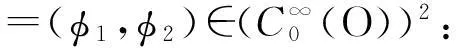
则V构成一个Hilbert空间.用V′来记V的对偶空间,用L(Χ,Y)来记从线性空间Χ到线性空间Y的所有有界线性变换构成的空间,用P来记从(L2(O))2到H的正交投影.

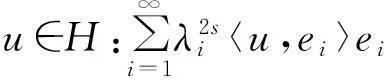
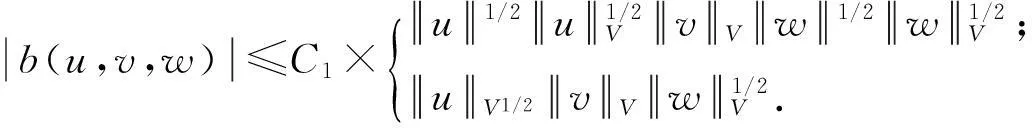
(2)

定义双线性映射B∶H×V→V′为〈B(u,v),ω〉=b(u,v,ω),∀ω∈V(把B(u,u)∈V′简记为B(u))，则方程(1)转化为抽象的随机泛函方程

(3)

对迫力项f施加如下假设条件:

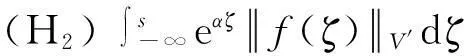
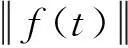
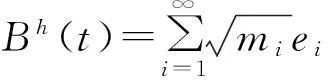
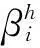
显然,该随机过程是H值Gaussian过程,起点值为0,有0期望,协方差算子为

E(Bh(s)Bh(t))=Rh(t,s)Q.

记(Φs)0≤s≤t是取值于L(H)的确定性算子族,则Φ关于Bh的随机积分为

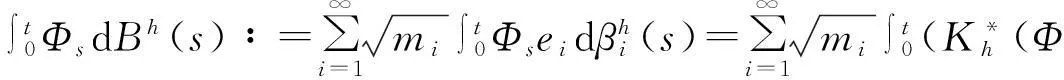
(4)

其中{βi}是相互独立的一维实值标准布朗运动序列.

如果一个函数u∈C([τ,T];H)∩L2(τ,T;V),对∀ω∈Ω,满足积分方程

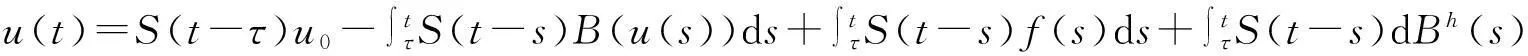
(5)

则称u为方程(3)的一个温和解.这里S(t)∶=e-At=∫e-λtdEλ,是由A生成的H的半群.在式(5)中等式右端的前两个积分是Bochner积分,第3个积分是式(4)定义的Wiener型积分,记为z(t).如果等式(5)右端的积分是良定的,那么它是线性随机方程dz(t)+Az(t)dt=dBh(t),z(0)=0∈H的唯一温和解.下面给出方程(3)的温和解的存在性.

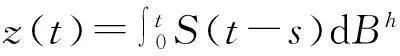
证明对z(t)在V上进行均方估计.

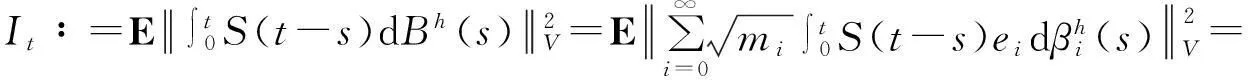
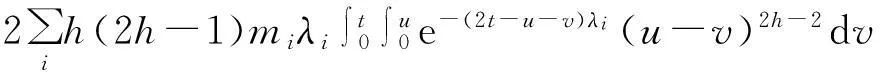
通过变量代换y=λi(u-v),得到

(6)

其中Γ(·)是Gamma函数.由假设条件(H4)可知,z在V中是良定的.

另外,对任意0≤s≤t,有

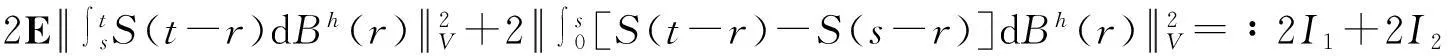
经过类似于式(6)的计算,得到：

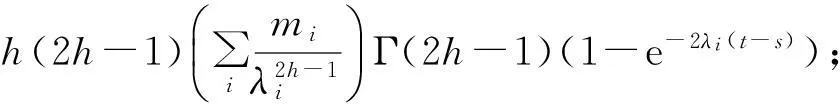
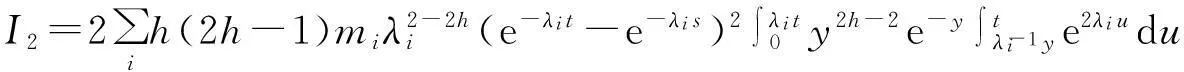
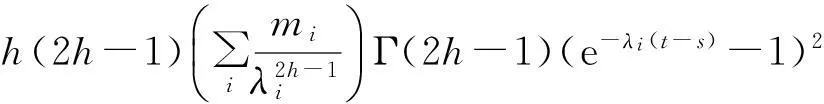
以上证明了均方意义下在V中的连续性.另外,z(t)是Gaussian过程,又因为S(t)是确定性算子,且对于∀u,v∈H, 〈S(t)u,v〉是关于t连续的,因此z(t)是可料的.证毕.

注2类似于文献[1-2],利用上面的结果可以证明,当假设条件(H3)和(H4)成立时,对∀u0∈H,ω∈Ω,τ∈R,积分方程(5)存在唯一解,使得u∈C(τ,∞;H)∩L2(τ,∞;V)，这就是方程(3)的温和解.

下面给出随机动力系统(RDS)及吸引子的有关概念,详细内容参见文献[3,7].

定义1设(Ω,F,P)是一个概率空间.称θ1是Ω上的一个保测流,如果一个映射θ1∶R×Ω→Ω为(B(R)×F;F)可测,并满足:(i)θ1(t)∘θ1(τ)=θ1(t+τ),∀t,τ∈R; (ii)θ1(0)=idΩ; (iii)θ1(t)P=P,∀t∈R.

以下把θ1(t)简记为θ1,t.关于保测流的存在性及其更多性质参看文献[8].本文把fBm看成是Ω={ω∈C(R,H):ω(0)=0},并把F看成是在Ω中关于紧开拓扑的Borelσ-代数,由于fBm是平稳增量过程,因此可以把θ1,t定义为

θ1,tω(·)=ω(·+t)-ω(t),t∈R.

定义2设{θ2,t}t∈R为一个非空集合X上的一族变换.如果θ2,0在X上是恒等映射,对∀t,s∈R,满足θ2,s+t=θ2,t∘θ2,s,则称θ2∶={θ2,t}t∈R为X上的一个参数流.

本文中根据需要,把上述定义中的集合X取为R,并把参数流θ2定义为θ2,t(s)=t+s.

定义3设E是一个完备度量空间.如果一个映射φ∶R+×Ω×R×E→E,满足：

(i)φ关于(B(R+)×F×B(R)×B(E);B(E))-可测;

(ii)φ(0,ω,τ,·)=idE,∀τ∈R;

(iii)φ(t+s,ω,τ,x)=φ(t,θ1,sω,θ2,s(τ),φ(s,ω,τ,x)),∀t,s∈R+,τ∈R,ω∈Ω,x∈E;

(iv) 对∀t∈R+,ω∈Ω,τ∈R,映射φ(t,ω,τ,·)∶E→E为连续.

则称φ为在E上的关于Ω的保测流θ1和参数流θ2的一个随机动力系统(RDS).

由注2定义由方程(3)诱导出的随机动力系统：

φ(t,ω,τ,u0)=u(t-τ,ω,u0)，

其中u(t-τ,ω,u0)是在τ时刻,以u0为初始条件的方程(3)的温和解.本文将讨论该动力系统吸引子的存在性，首先给出吸引子的相关概念.

定义4设E是一个完备度量的空间.一个映射K∶R×Ω→2E,如果对∀t∈R,x∈E,映射ω|d(x,K(t,ω))是关于σ-代数(F,B(R))可测的,则称K为可测的.其中d为Hausdorff半度量,(x,y).一个可测的映射K∶R×Ω→2E叫做在E上的依赖于时间的随机集合.如果对于∀t∈R,ω∈Ω,K(t,ω)是E的有界集合,则称K为有界的随机集合.如果对∀t∈R,K是P-几乎确定是紧的,则称K为随机紧集合.

假设φ为E上的一个RDS,K为一个随机有界集合.如果对任意有界集合B⊂E,存在依赖于集合B的随机时间tB(ω),当t

一个随机集合A,如果对任意t∈R+,有φ(t,ω,τ,A(τ,ω))=A(t+τ,ω), P.S.,则称随机集合A是关于φ不变的.如果一个关于φ不变的紧的随机集合A,对任意有界集合B,当τ→ -∞时,有d(φ(t,ω,τ,B),A(t,ω))→ 0, P-a.s.，则称A为φ的吸引子.

本文将利用下面的命题去证明方程(1)所诱导出的随机动力系统的随机吸引子的存在性.

命题2[9]如果一个随机动力系统φ拥有一个渐进紧的随机吸收集K,那么φ存在唯一的随机吸引子A,且A是K关于φ的Ω-极限集A(K,t,ω).

2随机吸引子存在性的证明

为证明随机动力系统φ的吸收集存在性与渐进紧性，首先引进改进的分形Ornstein-Uhlenbeck过程：

类似于命题1的证明,经过计算得

(7)

由此知Z(t)在V中是良定的，并且Z(t)是线性随机方程dZ(t)+(υA+a)Z(t)=dBh的唯一不变解.再由Birkhoff-Chintehin遍历理论,得

(8)

经过变量替换u(t,ω;τ)=v(t,ω;τ)+Z(θ1,tω),v(t)满足如下具有随机系数的确定性方程:

(9)

从u与v的关系式出发,对∀(t,ω,τ,u0)∈R+×Ω×R×H,得到如下关系式：

φ(t,ω,τ,u0)=u(t+τ,ω,τ,u0)=v(t+τ,ω,τ,u0-Z(θ1,τω))+Z(t).

下面分别在空间H和V中对v进行先验估计.

(10)

(11)

(12)

(13)

证明对方程(9)的第一式两端在H上与v(t)作内积,得

(14)

利用方程(2)的第一式,把三线性型b作如下估计:

(15)

利用Young不等式,得

(16)

(17)

(18)

利用Gronwall不等式,当t∈[s-1,s],τ

根据分形O-U过程的遍历性(8)可知

另一方面,由于

下面证明不等式(12)和(13).在区间[s-1,s]上对(18)式两端关于t作积分,得

因此,当τ

(19)

由此可得

(20)

证明在H上对方程(9)的第一式两端用A1/2v作内积,得

(21)

利用方程(2)的第二式,对b作如下估计:

(22)

利用Young不等式,得：

(23)

由式(22)和(23),不等式(21)变为

(24)

利用Gronwall不等式,对于s-1≤ζ≤s,有

(25)

(26)

由此证明了引理结论.证毕.

由引理1得出随机动力系统φ在H上存在随机吸引子.由于嵌入V1/2⊂H是紧的,因此,从引理2得出随机动力系统φ的渐进紧性.从而,得到如下结论：

定理1如果随机Navier-Stokes方程(1)满足假设条件(H1)—(H4),则随机动力系统φ拥有唯一随机吸引子A.

参考文献：

[1]FlandoliF.DissipativityandinvariantmeasuresforstochasticNavier-Stokesequations[J].NonlinDiffEqAppl, 1994,1(4):403-423.

[2]CaraballoT,LukaszewiczG,RealJ.Pullbackattractorsfornon-autonomous2D-Navier-Stokesequationsinsomeunboundeddomains[J].ComptesRendusMathématique, 2006,342(4):263-268.

[3]LiJ,HuangJ.Dynamicsofstochasticnon-NewtonianfluidsdrivenbyfractionalBrownianmotionwithHurstparameter[J].ApplMathMecha, 2013,34(2):189-208.

[4]SamkoSG,KilbasAA,MarichevOI.FractionalIntegralsandDerivatives[M].Switzerland:GordonandBreachSciencePublishers, 1993.

[5]BiaginiF,HuY, ØksendalB,etal.StochasticCalculusforFractionalBrownianMotionandApplications[M].London:Springer-Verlag, 2008.

[6]AlosE,MazetO,NualartD.StochasticcalculuswithrespecttoGaussiansprocesses[J].AnnProbab, 1999,29(2):766-801.

[7]韩英豪,王志鹏,于吉霞.随机Ginzburg-Landau方程的拉回吸引子[J].辽宁师范大学学报:自然科学版,2013,36(4):449-456.

[8]韩英豪,苏红,于吉霞.随机2-维纳维-斯托克斯-伯格斯方程的不变测度的存在性[J].延边大学学报：自然科学版,2013,39(3):161-166.

[9]CrauelH,FlandoliF.Attractorsforrandomdynamicalsystems[J].ProbabTheoryRelatedFields, 1994,100(3):365-393.

[10]MaslowskiB,SchmalfußB.RandomdynamicssystemsandstationarysolutionsofdifferentialequationsdrivenbythefractionalBrownianmotion[J].StoahsticAnalAppl, 2004,22(6):1557-1607.