基于虚拟阵列变换的共形阵列信号DOA估计
2016-01-10
(中国人民解放军92785部队,河北秦皇岛066200)
0 引言
共形阵列是一种与载体表面共形的天线阵列,由于其具有安装简化、波束扫描范围广、RCS小等优点[1-3],在现代飞机、导弹、卫星等设备均有重要的应用。共形阵列信号的二维角度估计问题是共形阵列信号处理中的重要内容,其在民用和军事上都有重要意义,已受到广泛关注。目前,国内外学者在共形阵列信号波达方向估计(Direction of Arrival,DOA)方面已经做了大量研究工作[3-10]。比如文献[3]以圆柱共形阵列为例,采用多维MUSIC谱估计方法实现了DOA估计,但其需要二维谱峰搜索,运算量大,不适用于工程实际;文献[4-7]通过合理划分阵列使其满足旋转不变结构,从而实现柱面阵列和锥面共形阵列的DOA估计。但其方法对阵列形状要求高,并不能适用于其他共形阵列。可以说,关于共形阵列信号DOA估计问题还有许多值得进一步研究的工作。本文给出了一种利用虚拟阵列变换的思想,采用ESPRIT算法和MUSIC算法相结合的方法实现了共形阵列信号二维角度估计。算法对阵列形状限制小,估计性能良好。以圆柱共形阵列为例,对算法性能作了仿真验证。
1 虚拟阵列变换方法
虚拟阵列变换方法[8]是将空间区域进行划分,针对某个感兴趣区域,在保证尽量小的变换误差下,将原始阵列接收数据变换为虚拟阵列接收数据。其主要是利用两个阵列导向矢量的变换关系获得阵列数据变换关系。由于经虚拟变换得到虚拟阵列是预先期望的,因此,可以使用一些经典的参数估计方法。从虚拟变阵列变换的原理上看,虚拟阵列变换方法适用于任意阵列。下面介绍一下虚拟阵列变换的实现过程。
对布置于三维空间中几何结构任意的阵列,如图1所示,假设感兴趣的区域为Θ=[θ1,θr],且信号位于此区域。

图1 布置于三维空间的任意阵列
将区域以间隔Δθ作均匀分割,即Θ=[θ1θ1+Δθθ1+2Δθ…θr-Δθθr],那么原始阵列的阵列流型矢量矩阵为
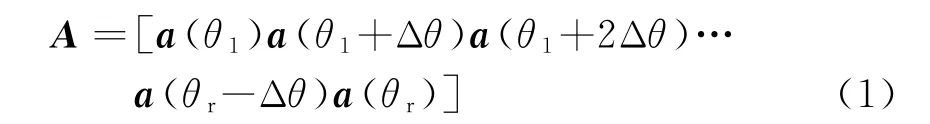
假设希望经过虚拟变换得到虚拟阵列的流型矢量矩阵为ˉA,则在同样的空间区间内,有

那么,原始阵列和虚拟阵列之间可以通过虚拟变换关系实现近似变换,即满足

同理,原始阵列和虚拟阵列的导向矢量之间存在如下关系:

显然,由原始阵列到虚拟阵列的变换过程中,会存在变换误差。因此,求取变换矩阵B,可以看作如下计算:
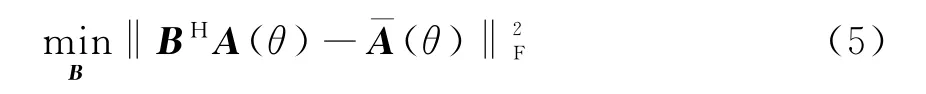
式中,‖·‖F为Frobenius模。
由式(3)~(5)可以求得虚拟阵列变换矩阵:

那么,变换误差可以定义为

显然,理想情况下,变换误差为零,此时虚拟变换过程是一个完全等价过程。但实际中,限于区域划分、区域划分间隔和虚拟变换阵列结构等限制,不可避免地存在误差。因此,在实际计算中,一般会设置一个误差允许范围。
下面看一下,通过虚拟阵列变换,数据协方差矩阵是否有变化。假设原始阵列的接收数据协方差矩阵为背景噪声为高斯白噪声,其功率为σ2I,则有

虚拟阵列的协方差矩阵可表示为
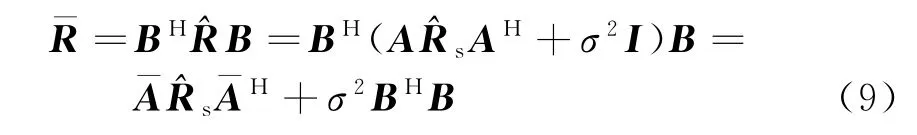
显然,从式(8)可以看出BHB≠I,即原始阵列白噪声被污染为色噪声。因此,要想利用虚拟阵列的协方差矩阵ˉR,必须预白化色噪声。那么可以将变换矩阵B修改为

那么,有THT=I成立。此时,式(3)和式(4)所表示的原始阵列和虚拟阵列的变换关系变为
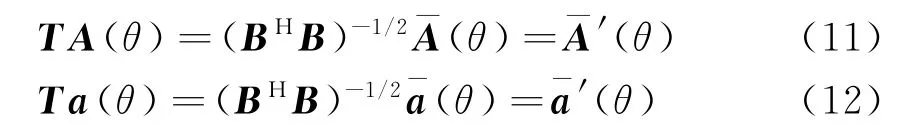
此时,虚拟阵列的数据协方差矩阵可写为

那么,利用式(13)得到的虚拟阵列协方差数据即可采用参数估计方法。需要注意的是,此时所对应的流性矢量矩阵ˉA′是经虚拟变换后的虚拟阵列的流行矢量矩阵。至此,对虚拟阵列变换方法作了简单的介绍。下面将介绍具体的参数估计方法。
2 基于虚拟阵列变换的角度估计方法
针对共形阵列,利用虚拟阵列变换思想,采用ESPRIT算法和MUSIC算法相结合的方法实现二维角度估计。
空间任意M元阵列如图2所示,第m个阵元的位置为p m=(x m,y m,z m)。假设有K个已知频率为f0的空间窄带信号源s1(t),s2(t),…,s K(t)入射到阵列,其入射角分别为{(θ1,ϕ1),(θ2,ϕ2),…,(θk,ϕk),…,(θK,ϕK)}。假设各阵元辐射方向图均为g(θ,ϕ)。当阵列存在较大曲率时,各阵元会受曲率影响,造成各阵元接收的信号强度不同。因此,这里将第m个阵元的真实接收方向图记为g′m(θ,ϕ)。
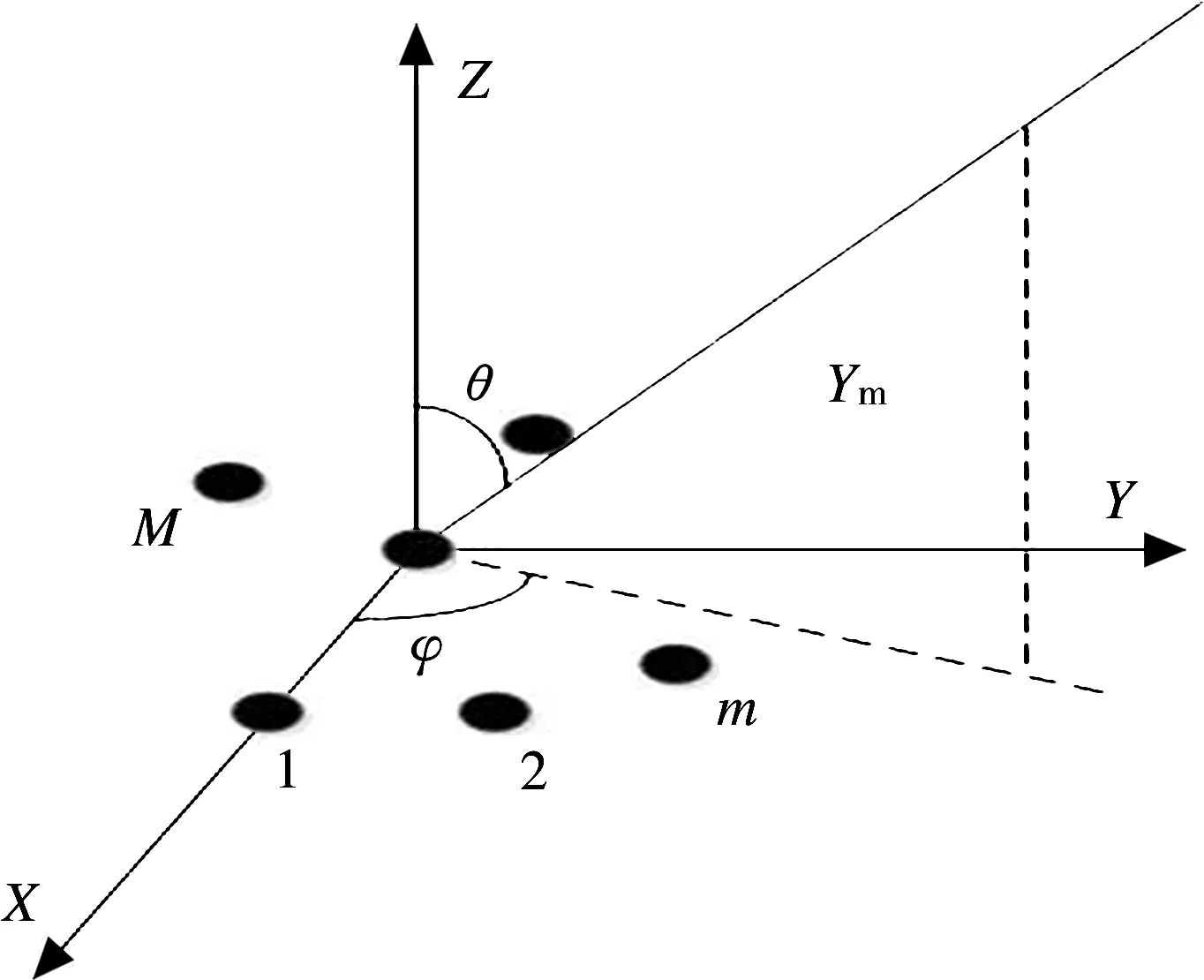
图2 空间任意M元阵列
首先确定希望虚拟变换后的虚拟阵列结构。考虑到实际共形阵列的几何结构可能多样,因此采用一种普适的方法。假设虚拟阵列的几何结构与原始阵列相同,只是沿着Z轴方向作了平移d z,令d z=λ/4。设虚拟变换的观察区域俯仰向为Θ=[θ1,θr],方位向为Φ=[φ1,φr],其中{θk∈Θ,ϕk∈Φ}。那么,原始阵列流型矢量矩阵A(θ,φ)和虚拟阵列流型矢量矩阵ˉA(θ,φ)有如下关系:
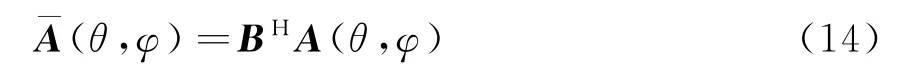
则虚拟阵列变换矩阵为

在获得虚拟变换阵列后,可以近似获得虚拟阵列接收数据。这样,相当于拥有了原始阵列和虚拟阵列两组接收数据。由于虚拟阵列与原始阵列存在固定的位置关系,可以采用ESPRIT算法[7]进行参数估计。这里仅是以沿Z轴方向作了平移,实际上只要保证虚拟阵列与原始阵列几何结构相同,同样可以将原始阵列沿着X轴或者Y轴方向作平移。
由于阵元方向图对算法无影响,这里将阵元辐射方向图认为是全向,则原始阵列和虚拟阵列的接收数据可以写成:
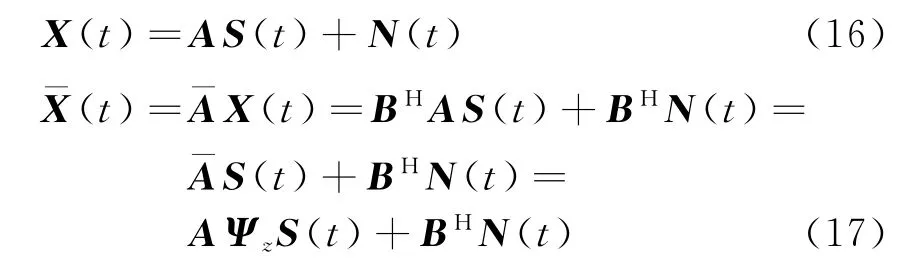
式中:S(t)=[s1(t),s2(t),…,s K(t)]T;N(t)为阵列接收噪声矩阵;

如果将两个阵列的数据模型合并,可得
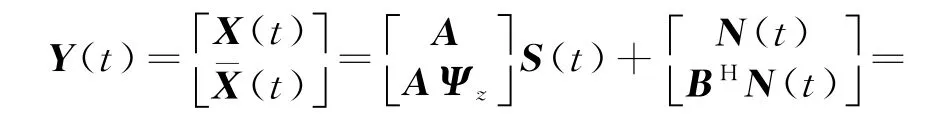
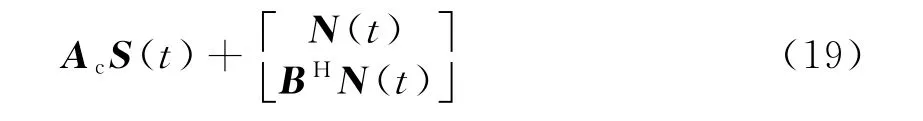
由旋转不变子空间原理,可知



由于原始阵列和虚拟阵列几何结构完全相同,由其旋转不变性,可以利用最小二乘的方法求出旋转不变矩阵Ψ:

对Ψ进行特征值分解,得到的K个特征值即对应着Ψz中对角元素,这样就可以求出K个入射信号的俯仰角。如果将原始阵列分别沿着X轴或者Y轴平移,作类似处理,就可以求出空间入射角的俯仰角和方位角。这里只利用沿着Z轴平移,求出空间入射信号的俯仰角度。设为对Ψ特征分解得到的第k个特征值,则信号的俯仰角可以通过下式求得:
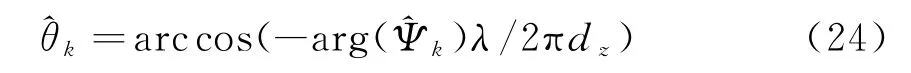
为了提高参数估计精度,这里采用文献[8]的方法,在获得信号俯仰角估计后,利用MUSIC算法作方位向的估计。由于采用虚拟阵列变换的方法,因此方位角搜索范围为Φ=[φ1,φr]。这是在小区间内的一维谱峰搜索,相比于全空间二维谱峰搜索,其运算量较小。
M USIC算法的谱估计公式为

至此,可以通过式(24)和式(25)对空间二维入射角进行估计。
下面给出算法主要步骤:
5)计算旋转不变矩阵Ψ,对Ψ进行特征分解;
6)由式(24)估计信号源俯仰角度;
7)根据估计出的俯仰角度和虚拟变换观察区域Φ=[φ1,φr]确定参数范围,对式(25)进行谱峰搜索,找到极大值即对应信号源入射方向。
3 仿真实验
圆柱共形阵列其几何结构是中心对称旋转体,根据文献[1]提出的子阵分割思想,将圆柱共形阵列进行分割,这样只需研究子阵性能即可。仿真采用如图3所示的3×3圆柱阵共形阵列,圆柱半径R=λ,信号波长λ=c/f0。共分3层,两层阵元间距d z=λ/4。每层阵元等角度分布,其相邻阵元夹角α=15°。阵元采用非极化全向阵元,即g(θ,ϕ)=|J2(πεsinθ)-J0(πεsinθ)|。根据阵列结构将观察区域作如下划分,俯仰向为80°~100°,间隔0.1°;方位向为5°~25°,间隔0.1°。虚拟阵列设置为原阵列沿Z轴正向平移λ/4。
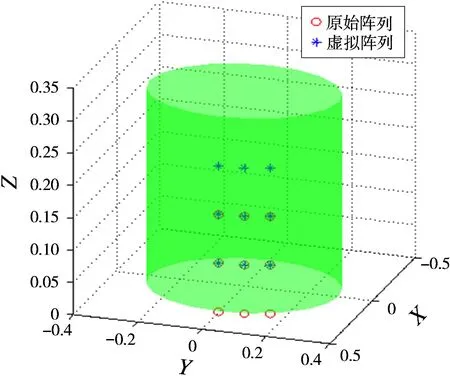
图3 圆柱共形阵列
设有2个频率为f0的空间窄带信号源入射到阵列,信噪比(SNR)均为20 dB,其二维角度参数(θ,φ)(其中,θ代表俯仰角,φ代表方位角)为(85°,15°)和(95°,20°),采样快拍数为500,伪快拍数为50,做50次蒙特卡罗仿真实验。图4是角度估计结果。
从图中可以看出,算法可以估计出信源的二维入射角度。同时看到估计存有偏差。定义信源k的角度估计均方根误差(RMSE)为
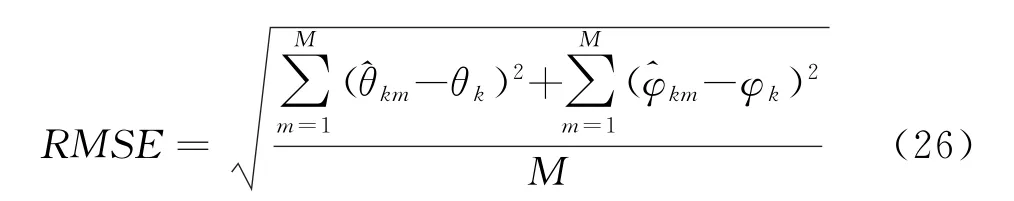
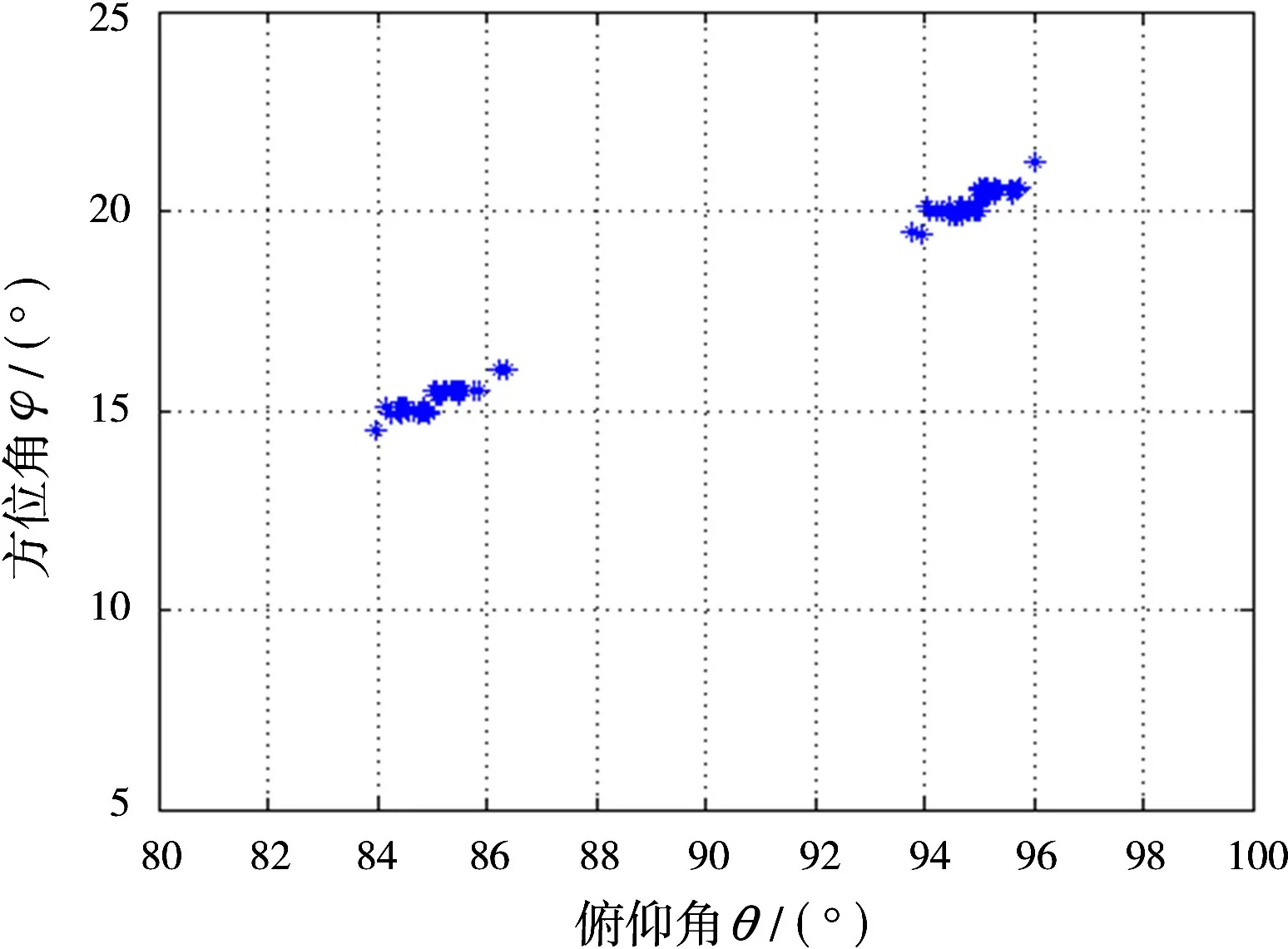
图4 角度估计结果
图5是角度估计误差随信噪比的变化曲线,可以看出,随着信噪比的增加,估计性能逐渐提高。在信噪比为25 dB开始趋于稳定。在仿真时发现,算法在低信噪比时性能较差,所以信噪比选择从10 dB开始。其误差主要受到虚拟变换误差和算法误差两个方面的影响。因此,两种算法均对信噪比存在约束。
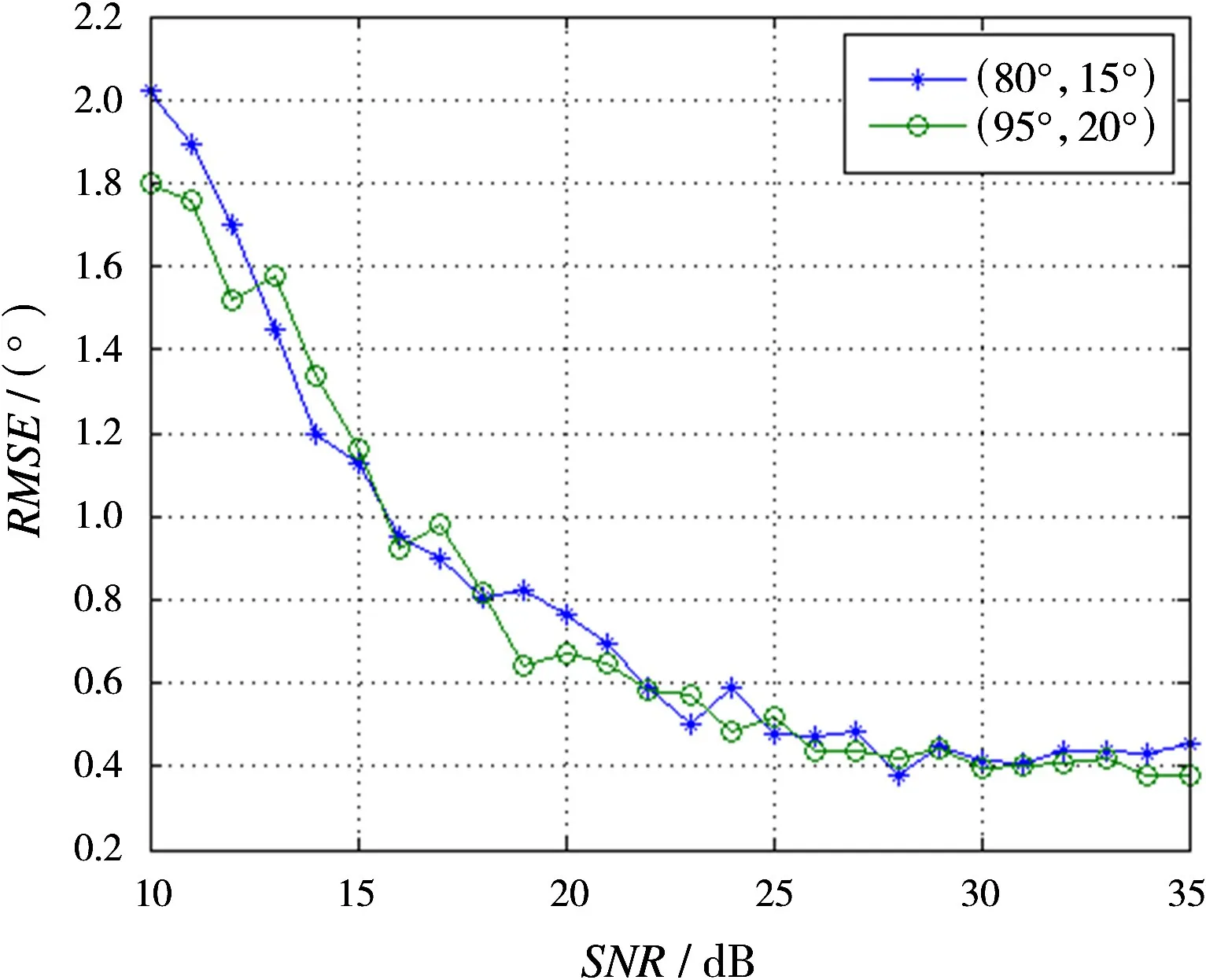
图5 角度估计结果的RMSE随信噪比变化曲线
图6是角度估计误差随采样快拍数的变化曲线。可以看出,当快拍数增加到900时,算法估计性能逐渐趋于稳定。

图6 角度估计结果的RMSE随采样快拍数变化曲线
4 结束语
本文利用虚拟阵列变换思想,采用ESPRIT算法和MUSIC算法相结合的方法实现了共形阵列信号二维角度估计。以圆柱共形阵列,通过仿真实验对算法有效性进行了验证。算法对阵列形状限制小,性能良好。关于共形阵列信号参数估计还有许多值得继续深入研究的工作,比如共形阵列信号极化、频率参数估计问题等。
[1]ZOU L,LASENBY J,HE Z.Direction and Polarisation Estimation Using Polarised Cylindrical Conformal Arrays[J].IET Signal Processing,2012,6(5):395-403.
[2]ZOU Lin,LASENBY J,HE Zishu.Pattern Analysis of Conformal Array Based on Geometric Algebra[J].IET Microwave,Antennas&Propagation,2011,5(10):1210-1218.
[3]齐子森,郭英,王布宏,等.共形阵列天线MUSIC算法性能分析[J].电子与信息学报,2008,30(11):2674-2677.
[4]郭英,高梅,张树银,等.基于旋转不变子空间原理的共形阵列DOA与极化状态联合估计[J].上海交通大学学报,2013,47(7):1137-1142.
[5]YANG P,YANG F,NIE Z P.DOA Estimation with Sub-Array Divided Technique and Interpolated Esprit Algorithm on a Cylindrical Conformal Array Antenna[J].Progress In Electromagnetics Research,2010,103(1):201-216.
[6]张树银,郭英,齐子森.锥面共形阵列信源方位和极化参数的联合估计算法[J].电子与信息学报,2011,33(10):2407-2412.
[7]SI W,WAN L,LIU L,et al.Fast Estimation of Frequency and 2-D DOAs for Cylindrical Conformal Array Antenna Using State-Space and Propagator Method[J].Progress In Electromagnetics Research,2013,137(1):51-71.
[8]王永良,陈辉,彭应宁,等.空间谱估计理论与算法[M].北京:清华大学出版社,2004.
[9]李杰然,许稼.共形阵列信号DOA和极化状态联合估计研究[J].雷达科学与技术,2015,13(2):159-163.LI Jieran,XU Jia.Joint Estimation of 2D-DOA and Polarization Based on Conformal Array[J].Radar Science and Technology,2015,13(2):159-163.(in Chinese)
[10]孙学军,张高毅,唐斌,等.基于二次虚拟内插的圆阵接收2D-DOA分离估计[J].电子与信息学报,2008,30(8):1890-1892.
