基于信号幅度的复杂目标新数据互联方法

(中航工业雷华电子技术研究所预研总体部,江苏无锡214063)

0 引言

现今海面作战环境日益复杂,特别是在目标密集且目标距离较近、目标RCS差异明显的环境下,对目标稳定跟踪提出了更严峻的挑战,特别是造成密集回波数据关联更加困难[1]。

目前数据关联方法主要分为两类:极大似然类数据关联和贝叶斯类数据关联。极大似然类数据关联主要包括航迹分叉法、联合似然法、广义相关法等;贝叶斯类数据关联算法主要包括NN,PDA,JPDA和MHT等[2-4]。其中JPDA算法被认为是一种比较完善的算法,但是随着虚警率、检测概率和目标密集程度的恶化,其误关联概率迅速增加。为此,Musicki等将航迹质量代入关联概率计算,提出了IPDA,JIPDA,LJIPDA和LMIPDA等一系列改进方法,以有效降低虚假航迹对关联结果的影响[5-6]。但是上述方法均未考虑利用目标回波的非运动学信息进行数据关联,这就造成了对目标回波信息利用不充分的弊端,难以进一步提高航迹跟踪精度。

本文提出一种基于目标信号幅度的数据关联方法,充分利用目标回波携带的非运动学信息——信号幅度[7-8],有效解决了虚警多、目标密集且间距较近、目标RCS差异明显等的数据关联问题。该方法首先建立信号幅度的数学模型,然后将其代入数据关联运算,最后通过仿真试验验证了算法的有效性。

1 幅度信息AI简介

由雷达测得并通过信号处理器输出端输出的信号强度叫做幅值信息(Amplitude Information,AI)。可以根据量测的幅度信息确认量测是否有效,即将幅度信息与设置的门限参数进行比较来判断量测的有效性。因而在目标密集且间距较近、目标RCS差异较大的复杂环境下,信号幅度能够有效区别有效量测和杂波,进而提高量测与目标准确关联的概率。

假设a为量测的幅度信息,d为信噪比,τ为幅度的检测门限为由目标产生的有效量测的幅度概率密度函数为仅有噪声(或杂波)的有效量测的幅度概率密度函数。定义幅度似然比λ(a)为

式中:

从式(4)可以得到,量测的幅度值越大,其量测的幅度似然比呈指数增大,因此,利用幅度似然比来改进数据关联算法和跟踪算法,可以提高目标的跟踪性能。

2 JIPDA-AI算法原理

JIPDA算法能够处理多航迹之间的互相干涉,这就表示至少两条航迹之间在一次特定的扫描中拥有一个共同的量测。在每步中,航迹被按组划分成群聚,每个群聚都是由量测唯一对应航迹组成的集合。测试群聚是所有航迹的集合,由于随着给定群聚内航迹数量的增加操作数也成指数增加,因而每个群聚应该控制航迹的数目。JIPDA算法原理如图1所示。

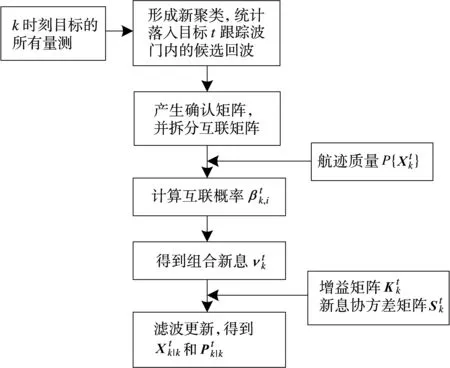
图1 JIPDA算法原理图

在JIPDA算法的基础上,加入幅度信息后可得到新算法JIPDA-AI,具体推导过程如下。

假设在Markov链下进行航迹质量变换,且不考虑航迹存在但不可见的情况,转移概率为π:

式中,p11+p12=p21+p22=1。

用T表示群聚中航迹的数目,m表示群聚中量测的总数,m t表示航迹t波门内的量测数目,V t表示航迹t的波门体积。群聚区域是个体波门的集合体,用V表示,即

式中,Vmax=max(V t)表示所有个体波门中最大的波门域。

群聚量测数目的先验估计为

根据量测与航迹波门之间的关系,可以拆分出很多互不相同的可行事件。可行事件的拆分有两个原则:

(1)每个航迹最多只能分配一个测量值;

(2)每个量测最多分配给一个航迹。

用χi表示互联事件i,X表示群聚中的互联事件的个数,T0表示在互联事件中航迹集合未分配任何量测,T1表示在互联事件中航迹被分配一个量测,则χi的后验概率为

若得到量测的特征信息中包含幅度信息,则可表示为

虚警在跟踪门体积V内服从均匀分布,而来自目标的量测服从高斯分布,包含幅度信息的量测j来自目标t的关联似然概率为

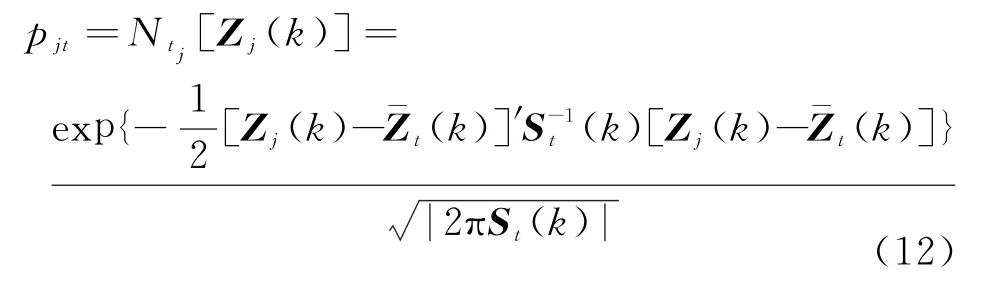
包含幅度信息的量测来自虚警的关联似然概率为

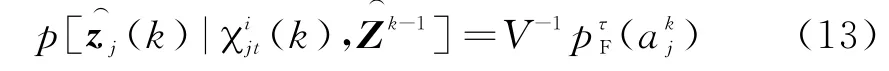
式中,V为跟踪门体积为只有杂波的有效量测的幅度概率密度函数。

那么,包含幅度信息的量测j源于目标t的关联似然概率为

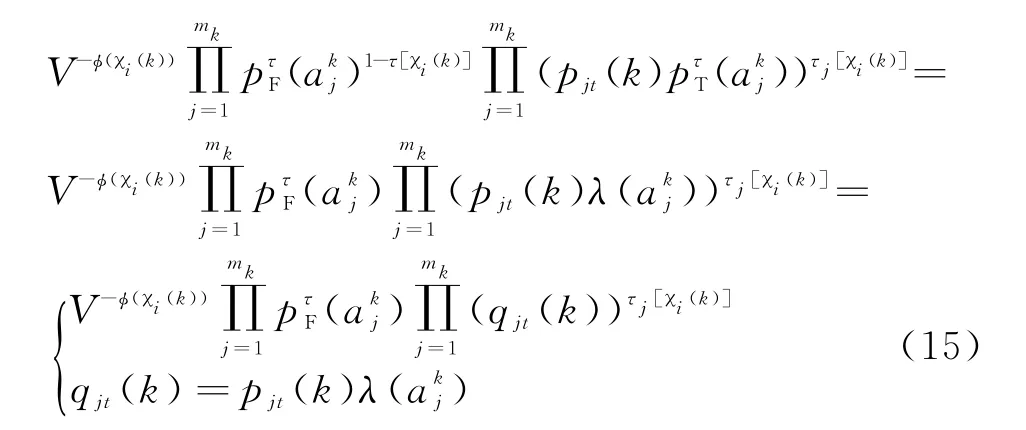
式中,m k为k时刻的有效量测个数,ϕ[χi(k)]为联合事件θi(k)中虚警的个数,τj[χi(k)]为量测互联指示变量(取0或1),δt[χi(k)]为目标检测指示变量(取0或1)。

引入特征信息幅度信息后的联合事件条件概率为

式中,c′为新的归一化常数。式(15)中由于在所有的可行联合事件中的值是相等的,因而可对其进行归一化处理。

个体航迹事件的后验概率密度可以通过求和包含该航迹事件的所有互联事件的后验概率得到表示航迹t互联量测i的所有互联事件集合,i=0表示无量测,因而集合可能为空。

无量测源于航迹t的后验概率为

航迹t存在且有量测源于航迹t的后验概率为

航迹t存在,但是无量测源于航迹t的后验概率为

估计航迹t的质量(存在的概率):

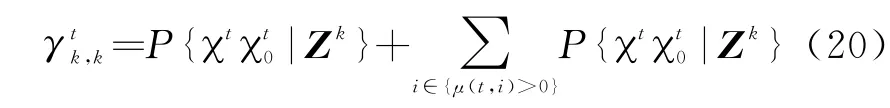
式中,{μ(t,i)＞0}表示落在航迹t的波门内所有的量测集合。则航迹t的β参数为

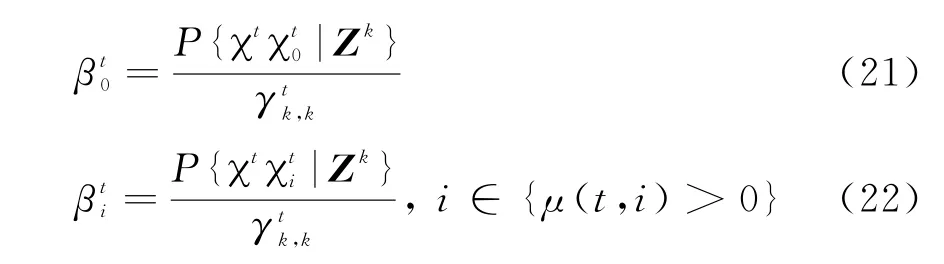
式中,参数β用于航迹估计。

目标状态更新方程为

估计状态预测协方差为

3 仿真环境及结果分析

为了详细讨论新算法JIPDA-AI的跟踪性能,设置3个目标的交叉运动仿真场景,如图2所示。3个目标具体运动轨迹如下:

目标1的初始状态为X(1)=(-29 500 m,400 m/s,34 500 m,-350 m/s),目标在1～40 s内作ω=0.02 rad/s的匀转弯运动,41～70 s内作ω=0.03 rad/s的匀转弯运动,71～100 s内作匀速运动。

目标2的初始状态为X(1)=(-29 500 m,296 m/s,34 500 m,-400 m/s),目标在1～40 s内作ω=-0.02 rad/s的匀转弯运动,41～70 s内作ω=0.03 rad/s的匀转弯运动,71～100 s内作匀速运动。

目标3的初始状态为X(1)=(-29 500 m,-400 m/s,34 500 m,-350 m/s),目标在1～40 s内作ω=0.02 rad/s的匀转弯运动,41～70 s内作ω=-0.03 rad/s的匀转弯运动,71～100 s内作匀速运动。

同时假定过程噪声分量q1=q2=0.01,雷达测距误差σr=100 m,测角误差σθ=0.02 rad;探测概率PD=0.98,门概率PG=0.9997,γ=16。试验观测间隔T=1 s,观测总帧数为100帧。

目标的运动方程为X(k+1)=F·X(k)+V(k),式中X(k)为目标的状态向量,F为状态转移矩阵,T为采样间隔,V(k)为零均值的高斯白噪声且协方差已知并满足E[V(k)V(j)]=Qδ(k,j),δ(k,j)为Kronecker△函数,Q为过程噪声协方差矩阵;航迹质量转移概率p=

经过50次Monte-Carlo仿真,图3、图4和图5分别给出了一次典型试验中JPDA,JIPDA和JIPDA-AI三种算法对目标1、目标2和目标3的X-Y方向跟踪均方误差曲线对比。

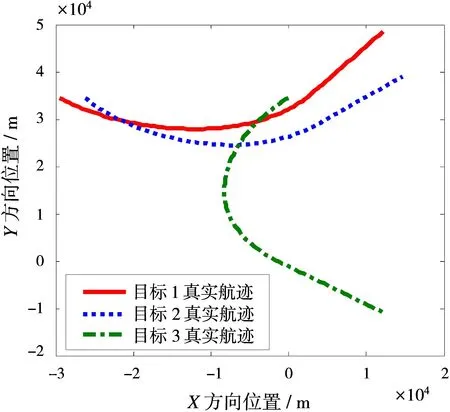
图2 目标运动真实航迹

图3 目标1的X-Y方向位置RMSE曲线对比

图4 目标2的X-Y方向位置RMSE曲线对比

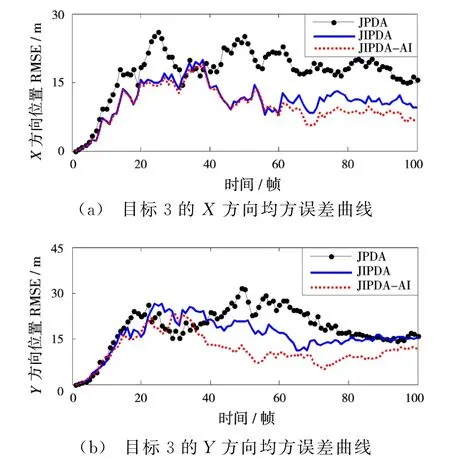
图5 目标3的X-Y方向位置RMSE曲线对比

从图3、图4和图5可以看出,JIPDA-AI算法相对于JIPDA算法和JPDA算法使得目标1、目标2和目标3的X-Y的均方误差RMSE明显降低,说明新算法能够有效降低跟踪误差。

从表1可以看出,JIPDA-AI算法对航迹1、航迹2和航迹3中的X方向位置RMSE误差比JIPDA算法分别降低13.8%,16.3%和17.0%,Y方向位置RMSE误差比JIPDA算法分别降低23.3%,20.5%和21.0%,由此可见新算法的跟踪误差较传统JIPDA和JPDA算法明显降低,从而提高了跟踪精度。图6为在某海港进行对海试验时,对采集的试验数据用新算法跟踪目标。

表1 JPDA,JIPDA和JIPDA-AI算法X-Y位置方向RMSE比较

图6(a)为采用传统的JIPDA算法处理的航迹跟踪图,图中119号目标为加了角反射器的快船目标的航迹,126号目标为未加角反射器的快艇目标的航迹,可以看到两目标在航迹交叉处均发生失跟现象。如图7所示,装有角反射器的119目标信号幅度明显高于未装角反射器的126号目标,易采用置信度区间的方法区分两目标尤其是在航迹交叉处的量测归属(将门限内的量测用于关联计算,门限外的则直接丢弃)。如图6(b)所示,新算法利用信号幅度信息辅助目标跟踪,两个目标的航迹分开。结果表明新算法比传统的JIPDA算法有更好的稳定跟踪能力。

图6 海面态势图

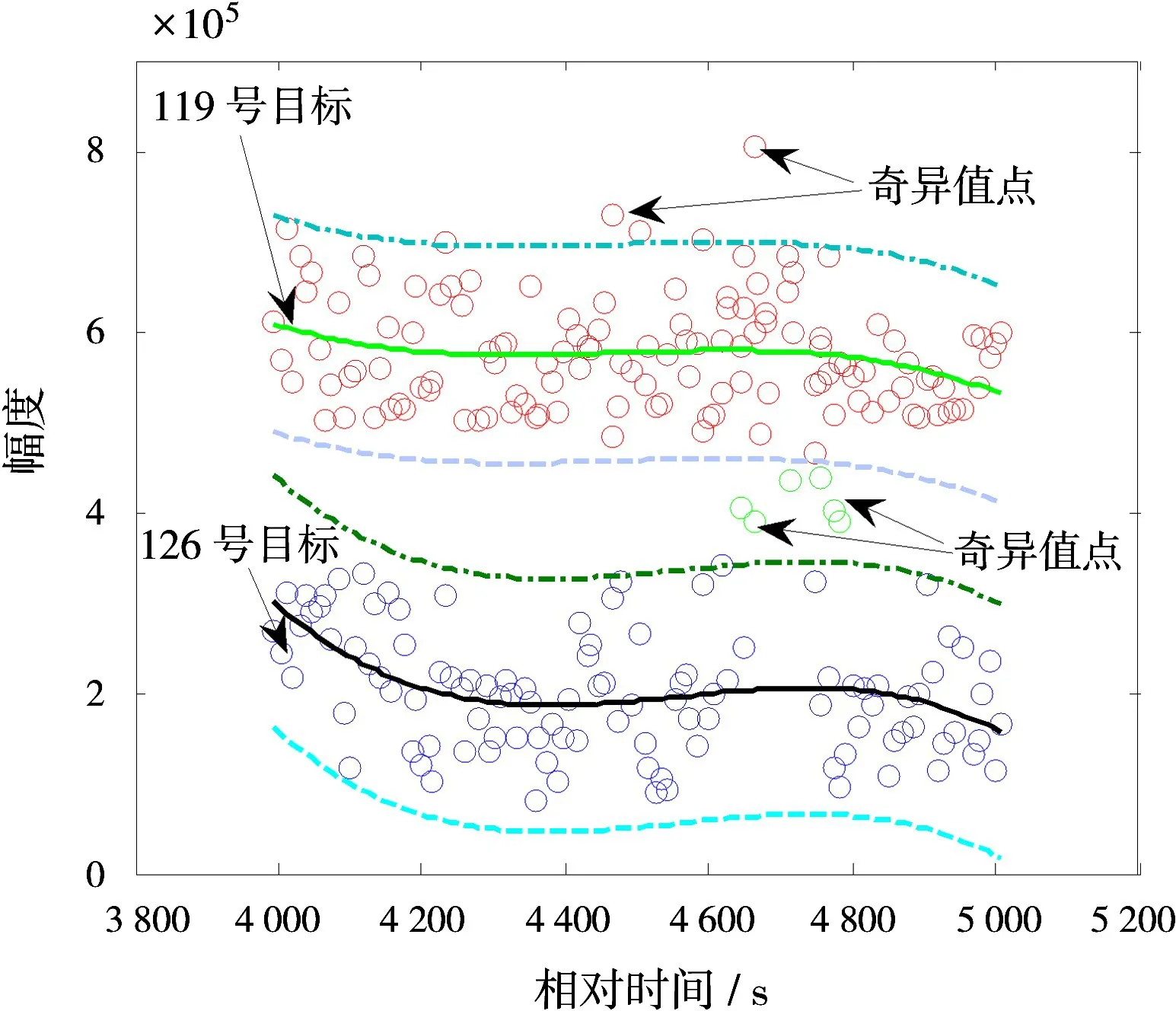
图7 信号特征参数幅度信息对比图

4 结束语

本文针对虚警多、目标密集且目标间距较近、目标RCS差异较大等应用环境下的数据关联问题展开研究,提出一种基于目标信号幅度的数据关联方法,该方法充分利用目标回波中的非运动学信息——信号幅度,建立起与互联概率的映射关系,给出了新的雷达量测与目标航迹的关联概率计算方法,最后仿真试验表明新算法能有效提高密集航迹的稳定跟踪能力。

[1]王云奇,孔令讲,易伟,等.一种耦合检测和JPDA滤波的多目标跟踪算法[J].雷达科学与技术,2014,12(2):143-148.WANG Yunqi,KONG Lingjiang,YI Wei,et al.Integration of Detection with JPDAF for Multi-Target Tracking[J].Radar Science and Technology,2014,12(2):143-148.(in Chinese)

[2]CHEN X,THARMARASA R,PELLETIER M,et al.Integrated Bayesian Clutter Estimation with JIPDA/MHT Trackers[J].IEEE Trans on Aerospace and Electronic Systems,2013,49(1):395-414.

[3]WILLIAMS J L.Marginal Multi-Bernoulli Filters:RFS Derivation of MHT,JIPDA,and Association-Based Member[J].IEEE Trans on Aerospace and Electronic Systems,2015,51(3):1664-1687.

[4]LIANG H.A Possibilistic Data Association Based Algorithm for Multi-Target Tracking[C]∥Third International Conference on Intelligent System Design and Engineering Applications,Hong Kong:IEEE,2013:158-162.

[5]MUSICKI D,EVANS R.Joint Integrated Probabilistic Data Association:JIPDA[J].IEEE Trans on Aerospace and Electronic Systems,2004,40(3):1093-1099.

[6]LIU Yao,ZHANG Wei,CHEN Mingyan.Near Neighbor Cheap JPDA IMM Based on Amplitude Information[C]∥International Workshop on Microwave and Millimeter Wave Circuits and System Technology,Chengdu:IEEE,2012:245-251.

[7]BREKKE E,HALLINGSTAD O,GLATTETRE J.The Modified Riccati Equation for Amplitude-Aided Target Tracking in Heavy-Tailed Clutter[J].IEEE Trans on Aerospace and Electronic Systems,2011,47(4):2874-2886.

[8]KOHLLEPPEL R.Ground Moving Target Tracking with Amplitude Derived Direction of Arrival Estimation Accuracy Information[C]∥9th European Conference on Synthetic Aperture Radar,Nuremburg,Germany:VDE,2012:267-270.

[9]谢金华,郑世友.复杂环境下相控阵雷达新数据关联方法[J].信息融合学报,2015,2(4):331-337.

[10]何友,修建娟,关欣.雷达数据处理及应用[M].3版.北京:电子工业出版社,2013:120-147.