考虑表面效应的纳米矩形薄板挠度解析解

考虑表面效应的纳米矩形薄板挠度解析解*

姜礼鑫，曹高峰，林浩

(中国石油大学(华东)储运与建筑工程学院，山东 青岛 266580)

摘要：将表面弹性理论引入到纳米薄板承受外载荷的变形分析之中，根据薄板的小变形理论建立考虑表面效应的纳米薄板弹性微分方程.采用级数展开法，求出承受均布载荷的四边简支板、两对边承受正对称分布弯矩的四边简支板和两对边承受反对称分布弯矩的四边简支板的挠度解析解.

关键词：表面效应；Young-Laplace方程；表面残余应力；表面弹性；挠度

文章编号：1007-2985(2015)06-0040-04

中图分类号：O48文献标志码：A

DOI:10.3969/j.cnki.jdxb.2015.06.010

收稿日期：*2015-08-26

基金项目：国家自然科学基金资助项目(11272357)

作者简介：姜礼鑫(1981—)，男，山东黄岛人，中国石油大学(华东)储运与建筑工程学院硕士生，主要从事微纳米力学研究.

为了成功地设计和开发出满足需要的纳米器件，需要更深入地了解材料和结构在纳米级尺寸下的力学行为.研究纳米结构的本质特征最直观、最有效的方法是纳米尺度下的力学实验.相关研究结果表明，纳米结构的力学行为与一般结构的力学行为有明显的不同.宏观尺度下，材料和结构的表面积与体积比较小，表面积效应对材料和结构变形的影响远远小于体积效应的影响.因此，大尺寸的材料和结构只考虑体积效应就能满足精度要求，但对尺寸达到纳米级的材料和结构，其表面效应的影响不可忽略[3-4].

只考虑体积效应建立起来的经典弹性力学理论必须加以修正后才能应用到纳米结构中.基于连续介质力学，Gurtin等提出了考虑表面积效应的弹性理论，与实验结果非常吻合，该理论目前已得到广泛采用.HE Jin等基于梁的表面层模型对纳米线发生静态弯曲时的变形进行了深入研究.JIANG L Y等将此理论推广到了Timoshenko梁，并综合讨论了表面弹性和残余表面应力对于梁的影响.ZHAO D M等基于经典的Euler-Bernoulli梁理论，考虑表面效应之后对梁的本构关系进行修正，画出了新的弯矩图和剪力图.LIU J L等提到了纳米尺度下表面弹性理论应用的新进展.LIU J L等[9-10]在考虑了表面效应之后，讨论了不同边界条件下纳米线的大变形行为，并对梁的粘附问题也作了深入研究.

笔者以Gurtin等提出的表面弹性理论为基础，建立考虑表面效应的弹性微分方程，在此基础上分析纳米级薄板在各种边界条件下的弯曲变形.

1纳米级矩形薄板挠度理论解析解

1.1 两对边简支纳米矩形厚板

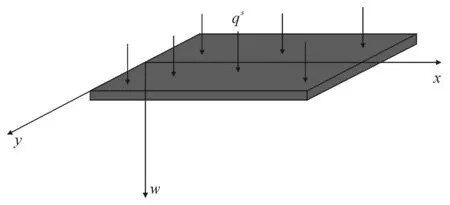
图1　考虑表面效应的纳米矩形薄板

承受均布载荷q的纳米矩形板(图1)，长边为a，短边为b，qs为考虑表面效应引起的压力.基于Gurtin的表面弹性理论，可以得到纳米矩形薄板的控制方程为

(1)

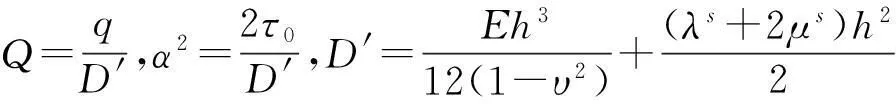
1.2 四边简支纳米矩形薄板

对于两边受正对称分布弯矩的纳米矩形薄板，当α2≠0，即τ0≠0时，(1)式的解为

对于两边受反对称分布弯矩的纳米矩形薄板，其求解方法与对称情况完全相同，当α2≠0，即τ0≠0时，(1)式的解为

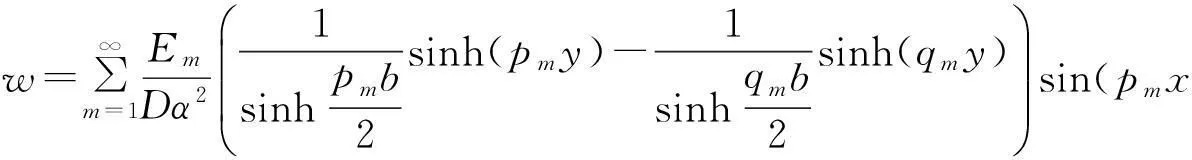
2仿真结果

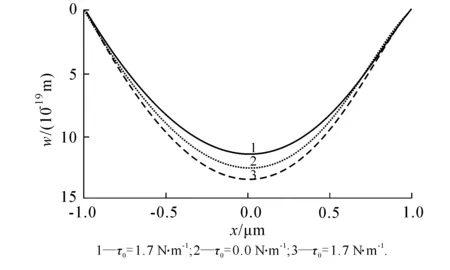
设参数E=177.3 GPa，υ=0.27，a=6 μm，b=2 μm，h=100 nm，λs=-8 N/m，μs=2.5 N/m，τ0=1.7，0，-1.7 N/m，q=100 μPa，y=±b/2，边界上对称均匀的弯矩M0=1×10-15N·m.画出以上各种情况下的挠曲面，用y=0和x=a/2这2个特殊平面去截挠曲面，得到四边简支板、四边简支板两对边受正对称弯矩和四边简支板两对边受反对称弯矩对应的挠度曲线(图2—4).

由图2—4可知，残余表面应力为负值时，矩形薄板的变形大于残余表面应力为0时矩形薄板的变形，并且随着残余表面应力的增加，板的变形逐渐减小；当残余表面应力增加到正值时，板的变形小于残余表面应力为0时板的变形.这说明正的残余表面应力增强了薄板的抗弯刚度，抑制了薄板的变形；负的残余表面应力减小了薄板的抗弯刚度，促进了薄板的变形.

a w(x,0)

b w(a/2,y)

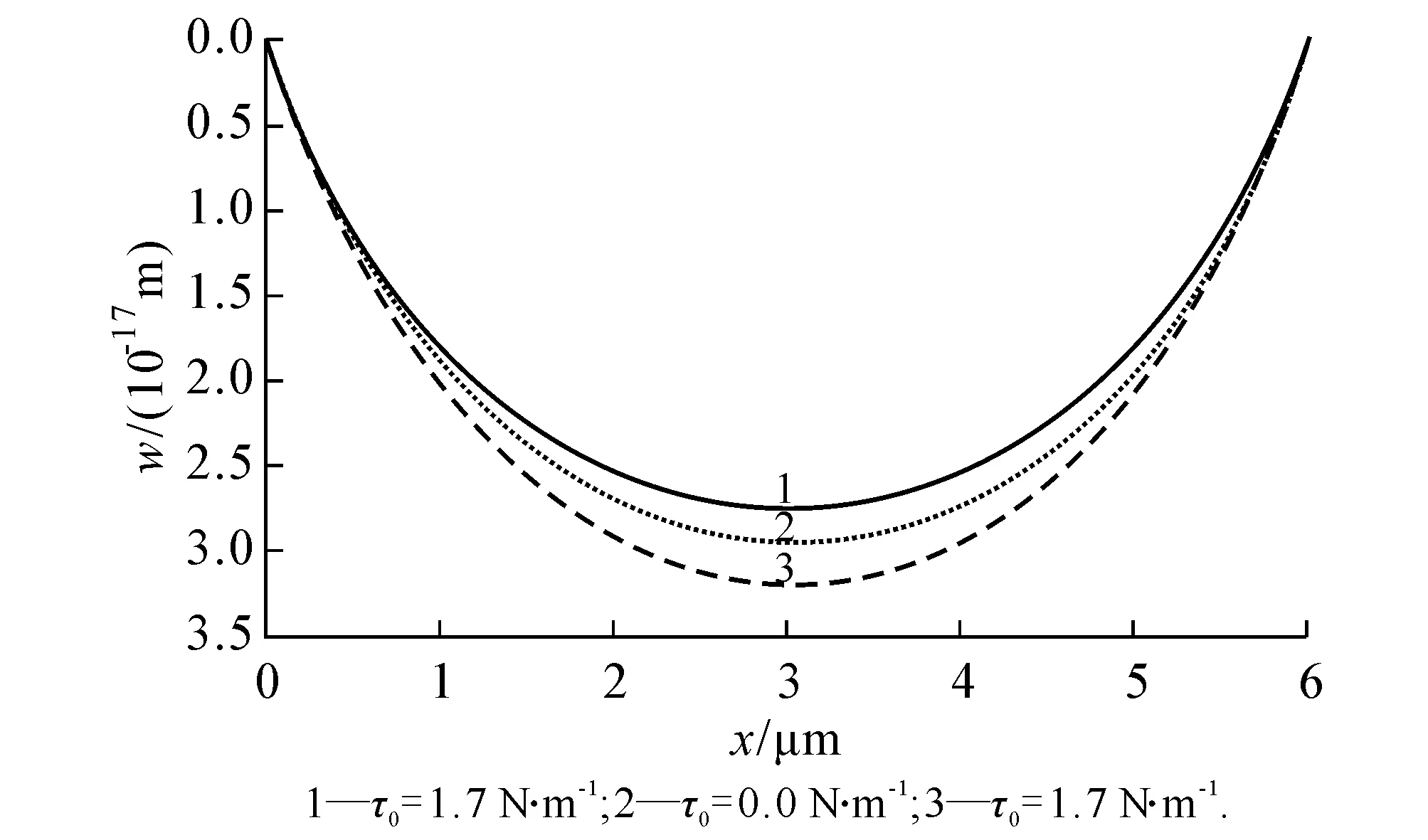
a w(x,0)

b w(a/2,y)

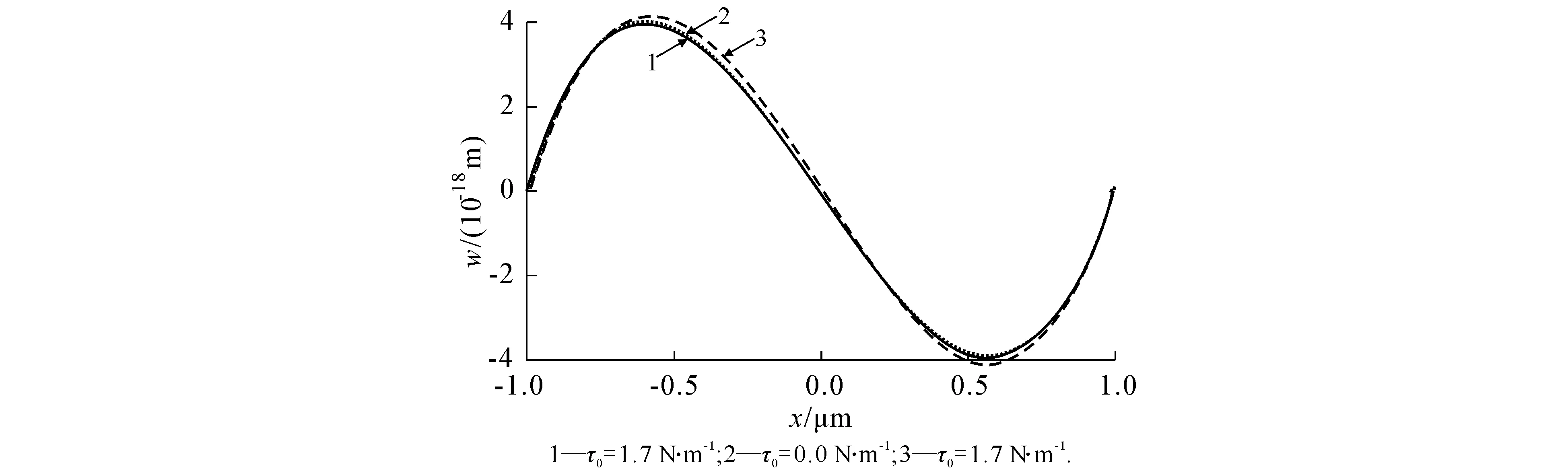
图4　两对边受反对称分布弯矩四边简支板的挠度曲线w(a/2,y)

3结语

基于Gurtin的表面弹性理论，考虑固体表面自由能对矩形薄板弯曲变形的影响，得到考虑表面效应的薄板小挠度弯曲弹性微分方程.笔者对承受均布载荷四边简支、两对边承受分布弯矩四边简支板进行了详细讨论，分别求得其挠度表达式，并将计算结果与经典弹性理论所得结果进行对比.仿真结果表明：残余表面应力为正值时，对薄板的抗弯刚度有增强作用，可以帮助薄板抵御变形；残余表面应力为负值时，对薄板的抗弯刚度有抵消作用，从而增加了薄板的变形.

参考文献：

[1]SUNCT，ZHANGH.Size-DependentElasticModuliofPlatelikeNanomaterials.JournalofAppliedPhysics，2003，93(2):1 212-1 218.

[2]DINGREVILLER，QUJianmin，CHERKAOUIM.SurfaceFreeEnergyandItsEffectontheElasticBehaviorofNano-SizedParticles，WiresandFilms.JournalofMechanicsPhysicsofSolids，2005，53(8):1 827-1 854.

[3]WANGGangfeng，FENGXiqiao.EffectsofSurfaceStressesonContactProblemsatNanoscale.JournalofAppliedPhysics，2007，101(1):013510.

[4]WANGGangfeng，FENGXiqiao.EffectsofSurfaceElasticityandResidualSurfaceTensionontheNaturalFrequencyofMicrobeams.AppliedPhysicsLetters，2007，90(23):231904.

[5]HEJin，LILLEYC.SurfaceEffectontheElasticBehaviorofStaticBendingNanowires.NanoLetters，2008，8(7):1 798-1 802.

[6]JIANGLY，YANZ.TimoshenkoBeamModelforStaticBendingofNanowireswithSurfaceEffects.PhysicaELow-DimensionalSystemsandNanostructures，2010，42(9):2 274-2 279.

[7]ZHAODM，LIUJL，SUNJ，etal.ARevisitofInternalForceDiagramsonNanobeamswithSurfaceEffects.CurrentNanoscience，2015,11(6):388-393.

[8]LIUJL，WURN，XIAR.SurfaceEffectsattheNanoscaleBasedonGurtin’sTheory：AReview.JournalofMechanicalBehaviorsofMaterials，2014，23(5/6)：141-151.

[9]LIUJL，MEIY，XIAR，etal.LargeDisplacementofaStaticBendingNanowirewithSurfaceEffects.PhysicaELow-dimensionalSystemsandNanostructures，2012，44(10):2 050-2 055.

[10]LIUJL，XIAR，ZHOUYT.StictionofaNano-BeamwithSurfaceEffect.ChinesePhysicsLetters，2011，28(11)：116201.

AnalyticalSolutionofRectangularPlateDeflectionwith

SurfaceEffectsatNanoscale

JIANGLixin,CAOGaofeng,LINHao

(CollegeofPipeline&CivilEngineering，ChinaUniversityofPetroleum，Qingdao266580,ShandongChina)

Abstract：Gurtin’s theory on surface elasticity was introduced into the deformation analysis of a thin plate at nanoscale under external loads.With small deformation theory，the differential equation of the nanometer-sized thin plate with surface effects was established.Analytical solutions of the deflection of a plate were obtained through series expansions，including the quadrilateral simply supported plate under uniformly distributed load，the quadrilateral simply supported plate with symmetrically distributed bending moment on the two opposite sides,and the quadrilateral simply supported plate with dissymmetrically distributed bending moment on the two opposite sides. The influence of the surface effects on the deformation of the plate was demonstrated.

Keywords:surfaceeffect;young-laplaceequation;surfaceresidualstress;surfaceelasticity;deflection

(责任编辑陈炳权)