夫妻围梯形桌入座问题

夫妻围梯形桌入座问题*

赵红涛，姜书丽

(华北电力大学数理系，北京 102206)

摘要：将Lucas夫妻圆桌问题推广为夫妻梯形桌问题(对夫妻围两边分别有1个和2n-1个座位的梯形桌入座)，得出该坐法的计数公式.

关键词：圆桌问题；直线桌问题；梯形桌问题

文章编号：1007-2985(2015)06-0001-04

中图分类号：O157.2文献标志码：A

DOI:10.3969/j.cnki.jdxb.2015.06.001

收稿日期：*2015-06-04

基金项目：国家自然科学基金资助项目(10901051,11201143)；中央高校基本科研业务费专项资金资助(13MS38)；华北电力大学教改项目资助(《高等代数》在数学建模中的应用)

作者简介：赵红涛(1978—)，男，河北沧县人，华北电力大学数理系副教授，博士，主要从事组合数学研究.

n对夫妻围圆桌入座问题是组合数学中一个非常著名的问题，学者们[1-5]用不同的方法给出了答案.赵立宽运用文献中创建的“积和式”方法解决了n对夫妻沿直线桌入座问题的坐法计数，但文中并没有给出坐法计数的具体计算过程.笔者给出了n对夫妻沿直线桌入座坐法计数的具体计算过程，并将n对夫妻围圆桌入座问题推广到n对夫妻围梯形桌入座问题，即n对夫妻围两边分别有1个和2n-1个座位的梯形桌入座 (n≥1).

1Pn的计算

文中所有入座问题的座位都已按顺序编号，不再一一赘述. 为了书写方便，定义如下符号：Mn为n对夫妻围圆桌入座问题的坐法计数；Pn为n对夫妻沿直线桌入座问题的坐法计数；Q1,n为n对夫妻围两边分别有1个和2n-1个座位的梯形桌入座问题的坐法计数.

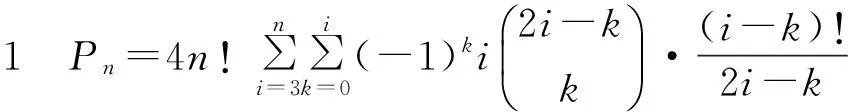
证明从文献已知

(1)

下面利用积和式给出Mn的另外一种表达方式.分3个步骤：

(ⅰ)确定座位编号为1的位置入座人的性别，有2种可能；

(ⅱ)不妨设男士坐在奇数编号的座位上，让n个男士入座有n!种坐法；

(ⅲ)对于男士入座的n!种坐法的每一种情况，给已经入座的n位男士按座位号的顺序分别标号1,2,…,n，他们的妻子对应编号1′,2′,…,n′.标号为i′的女士若可以坐在标号为j的男士的右边则记为aij=1，否则,记为aij=0.那么，n位女士的坐法对应如下矩阵：

根据乘法原则围圆桌入座问题方法计数

Mn=2·n!xn.

(2)

由(1)，(2)式可得

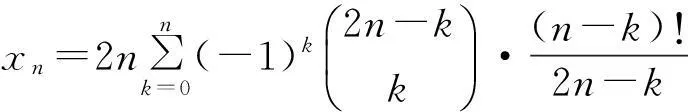
下面研究n对夫妻沿直线桌入座问题的坐法计数.同上，分3个步骤.不过对于此种情况，女士的坐法对应如下矩阵：

根据乘法原则，n对夫妻沿直线桌入座的坐法计数Pn=2·n!yn.下面根据yn与xn的关系计算yn.

yn按照第1行展开得

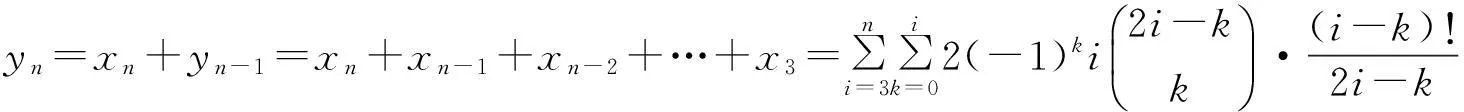
于是，n对夫妻沿直线桌入座问题坐法计数

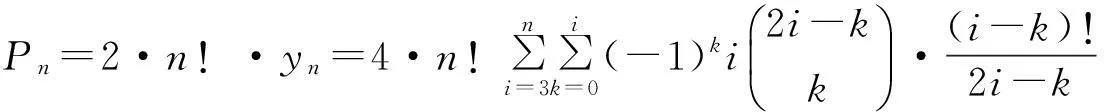
证毕.

2Q1,n的计算

证明首先给梯形桌短边的座位用1编号，然后给梯形桌长边上的座位用2,3,…,2n按从小到大的顺序继续编号.同定理1，分3个步骤，女士的坐法对应如下矩阵：

zn按第1行展开如下：

yn+yn-1=2yn-xn.

所以，

根据乘法原则，得到n对夫妻围两边分别有1个和2n-1个座位的梯形桌入座问题的坐法计数

证毕.

3结语

研究了Lucas夫妻圆桌问题的推广问题——围梯形桌入座问题(n对夫妻围两边分别有1个和2n-1个座位的梯形桌入座)，得到其坐法计数公式.而对于更为一般的围梯形桌入座问题，即n对夫妻围两边分别有l个和2n-l个座位的梯形桌入座(l≤n)，则是下一步的工作.

参考文献：

[1]谢孔彬.关于夫妻围坐问题.山东工程学院学报,1995(3):21-22.

[2]耿济.数学娱乐(一)——夫妻问题的新解与应用.海南大学学报自然科学版,2008(4):321-324.

[3]邵品琮.关于夫妻围桌入座公式的讨论.数学通报,1956(9):10-11.

[4]曹汝成.组合数学.第2版.广州:华南理工大学出版社，2012:58-60.

[5]郭茂祖，洪家荣.夫妻围坐问题的另一种解法.哈尔滨科学技术大学学报,1996(6):85-87.

[6]赵立宽.对夫妻直线入座问题的一个结果.曲阜师范大学学报:自然科学版,1992(1):65；87；90.

[7]于忠文.排列组合难题的正行列式解法.济南大学学报,1993(3):48-52.

Married Couples’ Trapezoidal Table Problem

ZHAO Hongtao,JIANG Shuli

(School of Mathematics and Physics,North China Electric Power University,Beijing 102206,China)

Abstract:In 1891,French mathematician Edouard Lucas gave his famous Married Couples Circular Table Problem:in how many ways can n married couples be seated around a circular table in such a manner that there is always one man between two women and none of the men is next to his own wife.In this article,we generalize this problem to Married Couples’ Trapezoidal Table Problem:in how many ways can n married couples be seated around a trapezoidal table with two sides having 1 and 2n-1 seats,respectively,in such a manner that there is always one man between two women and none of the men is next to his own wife.In this paper,the enumeration formula of this problem is obtained.

Key words:circular table problem;linear table problem;trapezoidal table problem

(责任编辑向阳洁)