一道自编题的进一步挖掘
2016-01-07黄良文
一道自编题的进一步挖掘
黄良文
(浙江省永嘉中学浙江 温州325100)
摘 要:对以往的一道以“带电粒子在电磁场中运动”为考点的自编题的进一步挖掘.
关键词:带电粒子电磁场挖掘
收稿日期:(2015-03-19)
笔者之前在本刊2014年第6期发表过一篇名为“一道‘带电粒子在电磁场中运动’命题的思路及体会”的文章[1],文章围绕“带电粒子在电磁场中的运动”的考点,以“心形”为设计轨迹,自编了一系列的计算题,供正在一轮复习的学生练习,学生做完后意犹未尽,甚至有学生尝试着自己出题.
都说兴趣是最好的老师,既然学生对这类题目有如此的热情,笔者决定对该题进一步挖掘,等过段时间学生对此类题型“淡忘”时再给他们来一次意犹未尽.
笔者依然用原来的题目框架将数据适当改变并将练习的标题命名为“我依旧”.实际给学生练习时,学生都会心地笑了,因为他们对这个“”特别有感觉.虽然学生记得轨迹为“心形”,但再次下手却没有想象的顺利,毕竟理科题目不是靠死记硬背,依然要仔细审题,结合知识点寻找解题思路.为了避免让学生形成“轨迹全都为对称结构”的思维定势,笔者最后一问专门设计了非对称的轨迹,也让学生体会到题目只需做小小的变动就有可能变得面目全非,但是解题的思路依然是如出一辙.
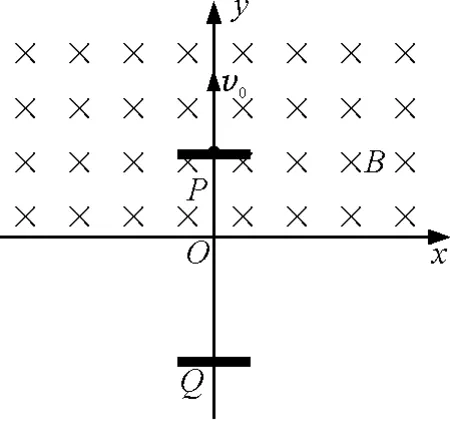
图1 题目插图

(1)在图中画出粒子的运动轨迹(作图中涉及到角度需写出必要的求解过程).
参考答案:设粒子从x轴上的S点离开磁场,由对称性可知
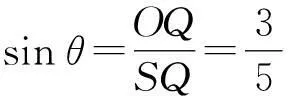
轨迹如图2所示.
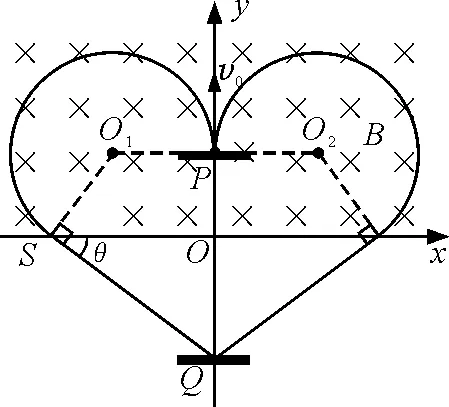
图2 第(1)问轨迹
参考答案:设粒子在磁场中运动的轨迹半径为r,周期为T,则
设粒子离开上挡板从P沿圆弧运动到S所用时间为t1,从S匀速运动到Q所用时间为t2,则
得
(3)若不借助下挡板,而采用磁感应强度也为B的半圆形匀强磁场,让粒子在离开半圆形磁场后依然沿原先的路线运动.则半圆形磁场的最小面积S为多大.
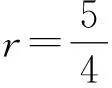
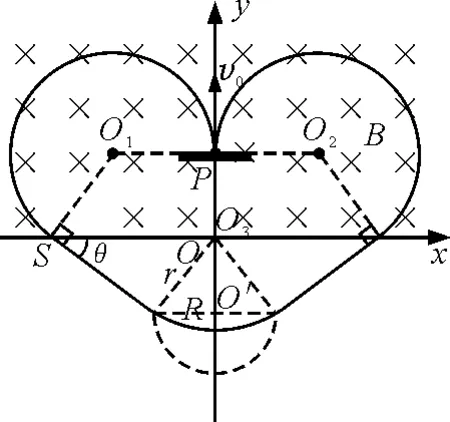
图3 第(3)问轨迹
当进入和离开半圆形磁场的位置的连线为半圆形磁场的直径时,磁场面积最小,设此时其半径为R,由几何关系可知
得
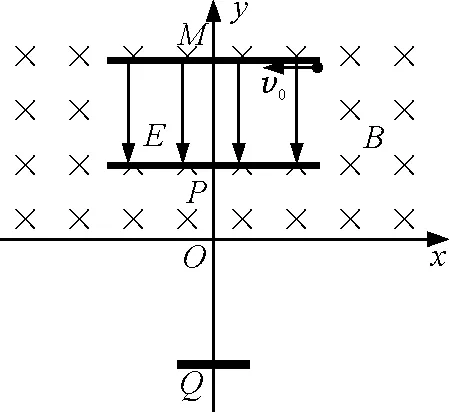
图4 第(4)问插图

参考答案:如图5所示,由对称性可知粒子在电场中的轨迹关于y轴对称.
设粒子进入电场到与下挡板碰撞经历时间为t,沿x轴方向
(1)
沿y轴方向
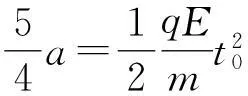
(2)
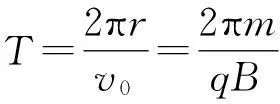
(3)
联立式(1)~(3),得
E=2Bv0
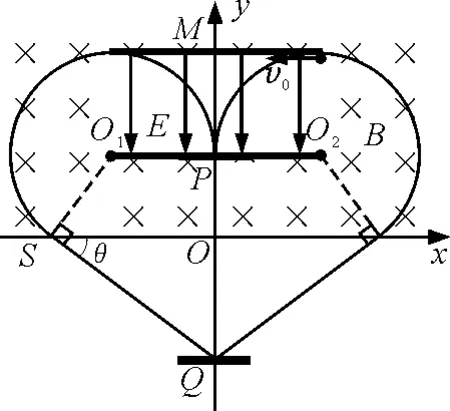
图5 第(4)问轨迹
(5)如图6所示,若在第三象限(不含y轴)加一沿x轴负方向的匀强电场,在第四象限(含y轴)加一等大沿x轴正方向的匀强电场,为使粒子能垂直撞向下挡板且离开电场后依然沿原先的路线运动,应将下挡板沿y轴向上或向下平移多大距离.
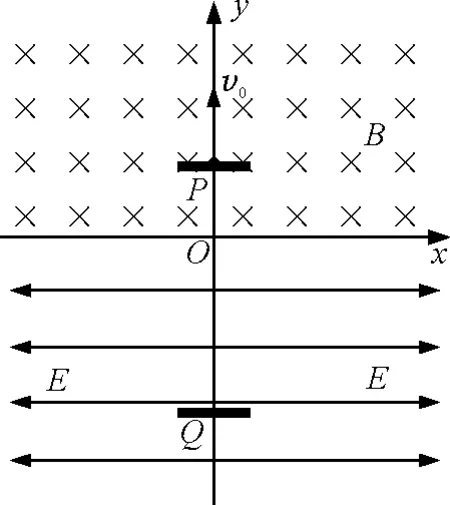
图6 第(5)问插图

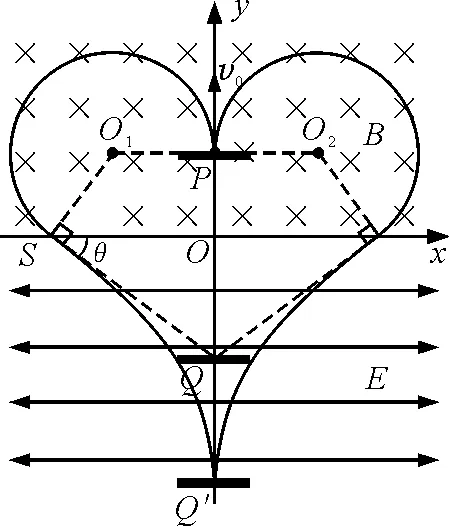
图7 第(5)问轨迹
(6)若在第三象限(不含y轴)加一沿x轴负方向的匀强电场,在第四象限(含y轴)加一等大沿x轴正方向的匀强电场,为使粒子撞向下挡板反弹离开电场后依然沿原先的路线运动,试求下挡板沿y轴向下平移的距离L的范围及场强E的大小范围.
参考答案:要使粒子返回磁场后仍沿原先路线运动,必须使粒子撞在下挡板的中点.
当E=0时,无需移动下挡板,即L=0.
本文根据RBC的特点,提出了ANP和证据理论的风险评估模型。将风险因素分为3个大类、11个小类,通过ANP分析风险因素的权重,充分考虑了风险因素之间的相互影响。通过计算折扣证据理论,在降低专家意见主观性的同时,实现对专家不同意见的有效融合。通过实例分析,验证了模型良好的适应性,该评估模型亦可用于其他信号系统。
当E取最大时,粒子刚好垂直撞向下挡板的中点Q′.
沿y轴方向
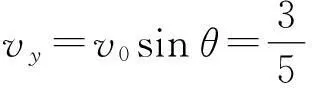
由类平抛规律可知Q为OQ′的中点
OQ′=2OQ=3a
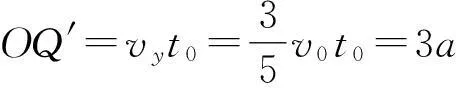
(4)
沿x轴方向
(5)
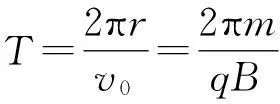
(6)
联立式(4)~(6),得

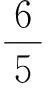
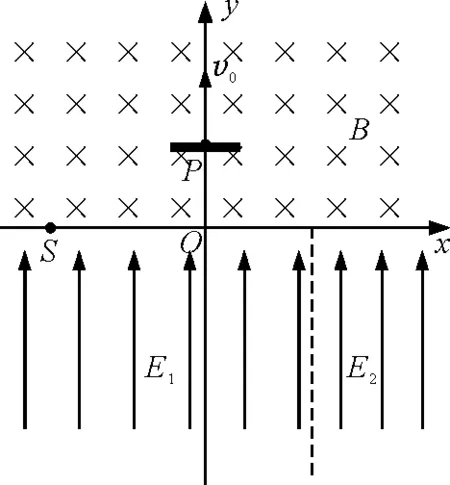
图8 第(7)问插图
参考答案:如图9所示,设粒子经N点返回磁场.
在第二象限磁场中,粒子轨迹半径为r1,有

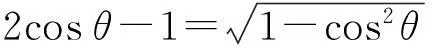

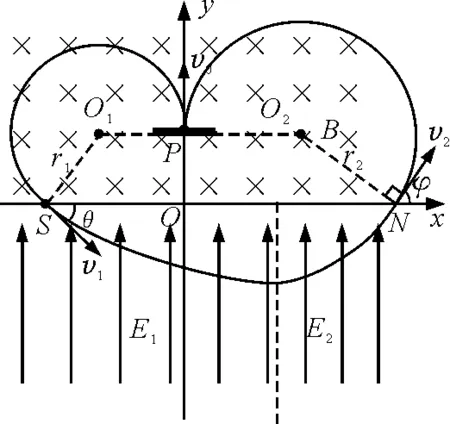
图9 第(7)问轨迹
在x轴下方,虚线左侧为逆向类平抛,右侧为类平抛.
虚线左侧电场中
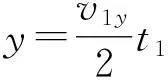
(7)

(8)
虚线右侧电场
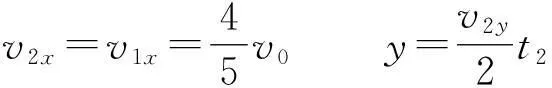
(9)
由式(7)、(9)得
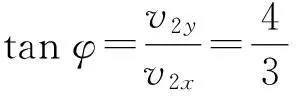
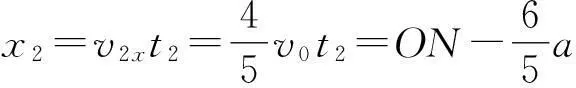
(10)
由式(8)、(10)得
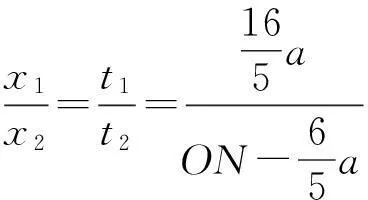
即粒子再次经过x轴的坐标为(3a,0).
第一象限磁场中
可得
粒子轨迹圆心O2离x轴的高度为
即与P点有相同纵坐标.
粒子最终回到与P点等高处时与N点的水平距离为

即与P点有相同横坐标.
所以最终粒子能回到P点.
参 考 文 献
1黄良文.一道“带电粒子在电磁场中运动”命题的思路及体会.物理通报,2014(6):45~48,51

