“电场高斯定理”的教学设计

“电场高斯定理”的教学设计

卫丽娜

(宁夏理工学院文理学院宁夏 石嘴山753000)

摘 要：高斯定理是大学物理中电磁学部分非常重要的一个定理.本文以非物理类理工科专业为背景，对大学物理课程中的高斯定理进行教学设计.

关键词：高斯定理教学设计

近几年，国内各大高校理工科专业大学物理理论教学课程面临教学学时压缩[1]，一些重要定理的推导和重要概念的理解也面临着教学学时“风暴”的侵蚀.大学物理课程中每节课的教学设计[2]尤为重要.本文以大学物理课程中“电场高斯定理”一节为例，依据教学大纲要求，精心设计了整个教学过程.

1教材分析

我校大学物理课程的教材是科学出版社出版的《简明大学物理》[3]，本书将“高斯定理”编排在第6章“静电场”的第2节，是整个电学部分两个基本定理之一.

在本节之前，教材已经介绍了库仑定律求解真空中静止点电荷周围激发的静电场问题，学生感觉利用该定律求解静电场在有些情况下比较复杂.本节内容安排了从特殊到一般的高斯定理的归纳过程，由特殊的以点电荷为球心的球面积分模型出发，进行不断变化，最终得出一般表达式，让学生亲身经历高斯定理的推导过程.根据电荷的分布特点，选择适当的高斯面，使用此定理能够更为方便地求出具有对称性分布的电场强度，将高斯定理与库仑定律联系对比，使学生认识到用高斯定理求解具有某种对称性的带电体周围分布的电场时较一般方法更加简单方便.同时，也说明了静电场是有源(发散)场.

电场中高斯定理的学习为之后稳恒磁场高斯定理的学习和理工科专业后续专业课程(比如电子信息工程专业课《电磁场与波》的学习)中计算电场强度奠定了基础，学生通过学习该定理能掌握科学的思维方法和研究方法，体验物理学中的对称和谐之美.

2学情分析

学生在学习本节之前，已掌握了利用库仑定律求解真空中静止点电荷周围的电场强度E，体会到利用该定律求解对数学尤其是积分运算要求较高且计算过程比较复杂.那么，求解带电体周围激发的静电场E是否还有其他相对简便的方法？静电场是否是有源场？这些都是要和学生共同解决的问题.更重要的是静电场和稳恒磁场的物理规律具有一定的对称性，静电场的学习将为后续稳恒磁场的学习做铺垫.

3教学目标设计

根据《大学物理》课程教学大纲的要求，结合我校理工科学生的特点，特制定如下教学目标.

知识与技能：

(1)深刻理解电场强度E的闭合曲面积分(或E的通量)与该闭合面所包围电荷之间的关系.

(2)电通量概念的理解和正负的判断.

(3)对于多个点电荷或连续分布带电体周围激发的电场，理解闭合曲面上E的本质内涵及表达式中正负电荷表示.

(4)掌握选取适当高斯面的方法及积分技巧.

(5)了解定理求场强的适用条件，熟练应用定理解决轴对称、球对称、面对称性分布带电体周围的电场问题.

过程与方法：

(1)师生互动共同推导高斯定理的数学表达式，掌握从特殊到一般的科学研究方法.

(2)经历利用高斯定理解决实际物理问题的过程，强调该定理的适用范围和注意事项.

情感态度与价值观：

(1)通过本节学习，特别是定理的得出过程，培养学生认真学习的态度、科学严谨推导的学习习惯，让班级形成善于思考、不断发现问题和积极解决问题的学习氛围.

(2)学生可以运用定理中学到的科学方法和研究能力，分析和解决以后学习、工作和生活中遇到的问题.

4教学重点及难点

教学重点：让学生经历高斯定理的推导过程，掌握利用定理计算电场强度的条件和方法.

教学难点：分析电场的分布特点，应用该定理优选适当的高斯面,积分求解电场强度.

5教学流程

5.1导入新课

师：通过电通量概念的学习，同学们已经知道电通量Φe的正负取决于电场强度和曲面法线方向夹角的余弦值，如果是闭合曲面(我们一般规定闭合曲面的外法线方向为正)呢？电场线从面元外穿进曲面里，此面元处电通量为负,否则为正.之前我们用库仑定律计算了在距离点电荷q为r处的电场强度为多少？

师：那么，我们现在计算一下整个闭合曲面的电通量到底等于什么？这也将是本节课的学习内容.

目的：从回顾学过的知识出发，让学生带着问题去学习思考.温故知新，并且让学生明确本节课的主要学习内容，即闭合曲面上E的通量等于什么？

5.2讲授新课

5.2.1推导高斯定理的数学表达式

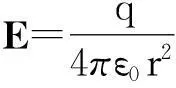
师生(以教师为主导，学生为主体)：

(1)

目的：利用双主互动教学模式[4]，定性复习了学生之前学习的孤立点电荷周围的电场分布并巩固了其数值表示.使学生更加了解知识的衔接，从而调动学生的求知欲.孤立点电荷的正负代换直接与结果正负息息相关，讲解过程形象、直观，更容易被学生接受.

师：孤立正点电荷在前面的球面外面，此时式(1)还成立吗？(注意观察球心对称位置处的E·dS)

目的：让学生对前面的推导结果进行延伸(拓展)，了解该结果在另外情况下是否适用，从而更加深学生对新内容的印象，即闭合球面以外的孤立点电荷对E的通量没有贡献.

师：在孤立点电荷周围电场中，∮SE·dS等于孤立点电荷除以真空介电常数ε0.如果是多个点电荷同时存在，那么周围的电场如何分布？此时E的通量又是多少？

目的：多个点电荷同时存在时，引导学生基于电场强度的矢量性和叠加性，正确推导出闭合曲面积分的结果.不仅得到了较复杂情况下高斯定理的表达形式，同时进一步加深了前面讨论的电场强度通量积分值的两个关键因素——“闭合面包围的点电荷”和“电荷的正负”.这种由简单到复杂的讲解方法，让学生更容易掌握新知识.

师：大家会有疑问，如果闭合面是任意形状呢，闭合面的积分数值是否符合上述数学形式呢？

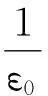
目的：在给出高斯定理数学表达式的同时，充分体现了教学的科学性和严密性，将课堂自然延伸到课外.

生：那么如果是连续分布的带电体呢？

师：问得好，这时候就要知道连续分布带电体电荷密度函数，然后对带电体积分得到带电体的电荷.具体问题我们将在课后习题作业中给大家解答.

目的：这更加体现了学生积极主动跟着教师思考问题，使我们的课堂知识不再仅仅是教师的教学为主，而是教师和学生相互“激发”，使教学相长，这也是课堂教学目的所在.

5.2.2定理的应用

关键词师：准确应用高斯定理解决电场分布问题时，要充分理解定理表述中的几个.一是“真空中电场”，指该定理数学表达式ε0；二是“闭合曲面”，简称“高斯面”；三是“电通量Φe”，只与包围在闭合曲面内的带电体有关；四是“闭合面上的电场强度E”，是指空间内存在的所有带电体共同激发的；五是“代数和”，指正负电荷代数和.

收稿日期：(2015-03-10)

师：对照这些强调点，请同学们利用高斯定理求解无限长均匀带电直线的电场分布,电荷线密度为λ(λ为常量).首先，在这一实际问题中定理是否适用？

生：对称性电场，定理适用.

师：选择怎样的闭合曲面？

生：以无限长均匀带电直线为轴，作半径为r，高为L的圆柱形闭合面.

师：那么此圆柱闭合面内包围的电荷如何计算？

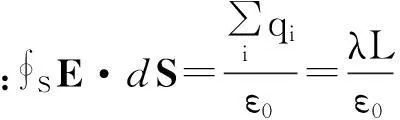
师：所求场点电场强度的大小等于多少？

目的：让学生与教师同步，主动参与例题的求解，理论联系实际，能使学生更好地理解和掌握定理，从而达到最终的教学目标.同时，有意识地培养学生的归纳演绎能力，以及严谨的学习态度.

6设计的创新点

本节内容教学设计在教师的引导下发现问题、分析问题和解决问题，避免了传统单一式即教师讲学生听的教学方法的弊端，能较好地活跃课堂气氛，达到学生积极主动地接受并运用知识的目的，这也是教师教育的目的所在.此外，通过本节课的学习，学生可以掌握物理中归纳、总结、演绎和类比的科学方法，对后续学习专业课有积极辐射和铺垫作用.

参 考 文 献

1刘熹微，罗贤清. 少学时大学物理教学改革的探索.科技资讯，2011(26):191～192

2张峰.“圆周运动”探究式教学设计.物理通报，2009(10):29～32

3张丹海. 简明大学物理(第2版).北京：科学出版社，2008.151

4李兴平.“双主互动”合作教学模式在物理教学中的探究.中国科教创新导刊，2010(16):76