用玻尔兹曼因子方程对“临界点 沸点 熔点”特性进行数值计算

用玻尔兹曼因子方程对“临界点沸点 熔点”特性进行数值计算

吴义彬

(南昌市老科学技术工作者协会江西 南昌330003)

摘 要：应用气体、液体与冰的玻尔兹曼因子方程, 对自然界物质在“临界点、沸点、熔点”时的物理特性进行数值计算,结果与观测值高度吻合.事实证明,简明的数学语言可以在很宽的温度范围内准确描述自然界物质物态变化的客观规律;玻尔兹曼因子方程是更具普适性的物态方程.

关键词：玻尔兹曼因子方程临界点沸点熔点物理特性

收稿日期：(2014-08-31)

1引言

“热力学的统计理论基础的发展是19世纪物理学的卓绝成就之一.虽然，这个发展的许多观念都源出于麦克斯韦和玻尔兹曼，但正是吉布斯的工作更直接地影响着我们现代对平衡态统计力学的表述”[1]; “在统计物理学中，物态方程可以根据系统内微观粒子的属性采用吉布斯的系综方法获得.然而，从单个粒子属性到理论上计算出系统的宏观量并不是一个很简单的问题，需要根据粒子的特性建立统计模型，求出系统平衡时处在各微观态的概率分布函数，然后由分布函数计算出各微观量的统计平均，即宏观量.在利用分布函数求统计平均时往往还需要利用各种近似算法.”[2]要在定量上得到精确的计算结果,更加“不是一个很简单的问题”！

与“系综方法”不同，直接从玻尔兹曼分布出发，在平衡体系边界区域的表面保守力场中应用玻尔兹曼分布，导出分别描述气体与液体的玻尔兹曼因子方程，不仅可以对液体的相变潜热[3]、表面张力系数及其温度变化率[4]等在定量上进行准确的数值计算，而且也可以对自然界物质在“临界点、沸点、熔点”时的物理特性进行准确的数值计算.

2临界点特性——气体临界系数存在趋同的特性

在临界点上，由于液体的摩尔体积Vim与饱和蒸汽的摩尔体积Vqm相同,等于气体的临界摩尔体积Vgmc,故描述摩尔气体的玻尔兹曼因子方程[5]变为

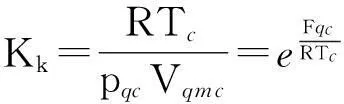
(1)

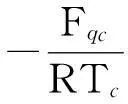
3临界点特性——液体表面张力系数都等于零

从饱和蒸汽压下单元液体玻尔兹曼因子方程出发,推导出了描述液体表面张力系数的数学公式[4]

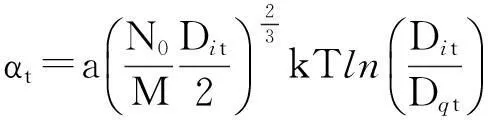
(2)

式(2)表明, 液体表面张力系数αt是温度T,液体密度Dit与饱和蒸汽的密度Dqt的函数.由于临界点上“液体及其饱和蒸汽间的一切差别都消失了”[7], 液体的密度与饱和蒸汽的密度相等, 即

由式(2)得液体表面张力系数αtc=0.

式(2)用精确的数学语言表明: 在临界点上,液体的表面张力系数都等于零.与临界点上“表面张力系数等于零[7]”的实验观测结果完全吻合．

4临界点接近于0K物质的特性——液氦的表面张力极小

“氦原子间的相互作用(范氏力)和原子质量都很小，很难液化，更难凝固.富同位素4He的气液相变曲线的临界温度和临界压强分别为5.20K和2.26大气压，1个大气压下的温度为4.215K;温度从临界温度下降至绝对零度时,液氦始终保持为液态，不会凝固.”

由于液氦仅仅在接近于零的0～5.20K温度区间内存在, 液气共存时的饱和蒸气压 ≤2.26大气压, 与液氦的临界温度、压强相差无几,“普通液氦的折射率和气体差不多，因而不易看到它”; 所以液氦的密度Dit与其饱和蒸汽密度Dqt相差极小, 所以:

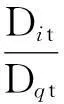
简明的数学语言式(2),对定量计算液氦的表面张力系数也是正确有效的.

5沸点特性——沸点摩尔气化熵大同小异 通常约为10R

5.1沸点摩尔气化熵的数值计算

由饱和蒸汽压下单元液体玻尔兹曼因子方程,可以导出沸点摩尔气化熵的数学公式[3]

(3)

先应用式(3)定量计算液体沸点摩尔气化熵(ΔS理沸),再与用沸点时气化热的实验观测值λ沸直接计算出来的沸点摩尔气化熵(ΔS实沸)相对照，列于表1[3].

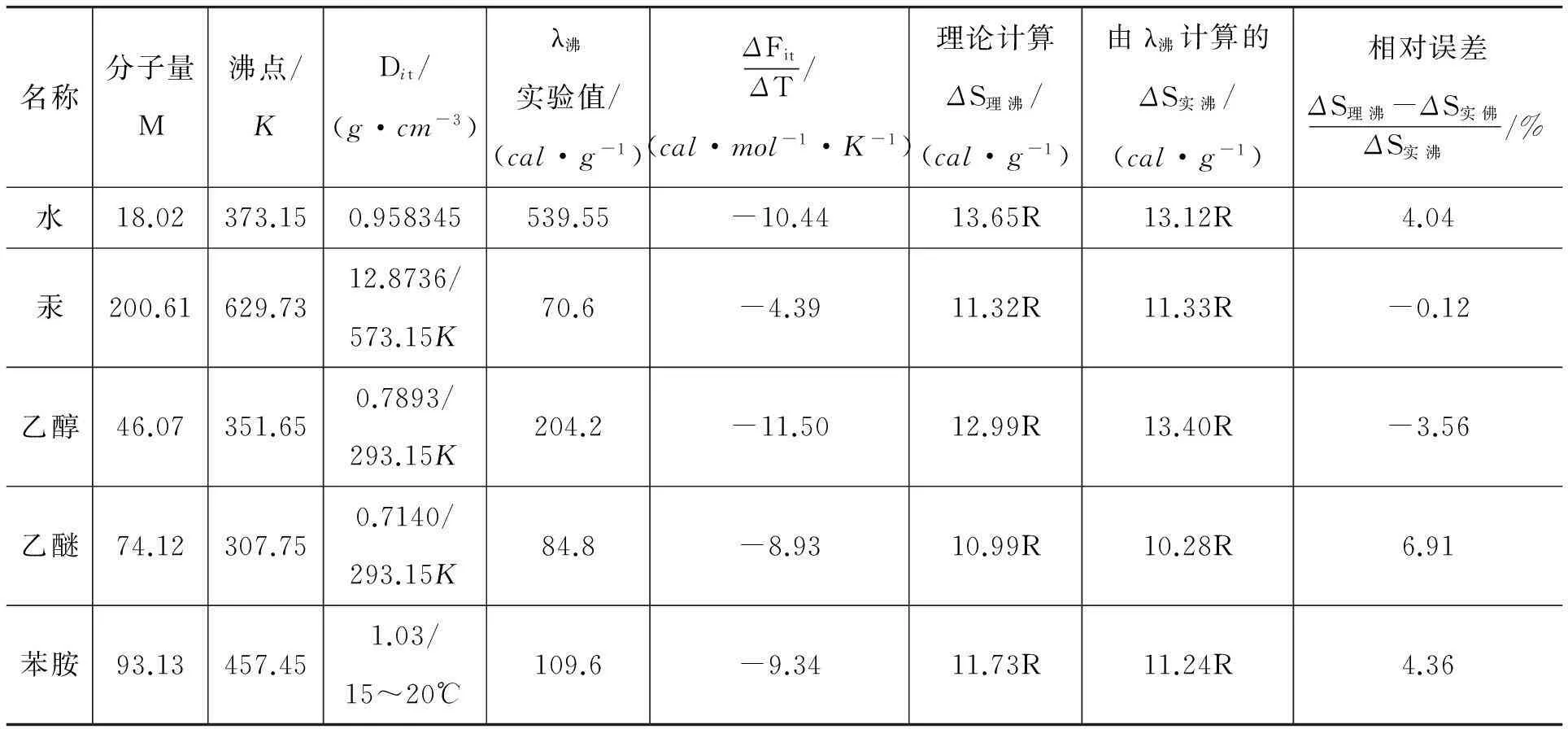
表1　纯物质沸点摩尔气化熵的理论计算

表注：ΔS理沸,ΔS实沸,可由表中数据直接代入下列两式求出

表列数据表明：尽管水、汞、乙醇、乙醚、苯胺5种液体的物理性质迥异，沸点时的T,Dit,M等宏观参量的数值相差很大，式(3)定量计算的结果ΔS理沸与实验观测值计算的结果ΔS实沸, 却吻合得很好, 均近似为常量.

5.2验证褚鲁统规则

“褚鲁统规则是一个有关液体的典型规则.它指出，在沸点下，一般液体的克分子蒸发熵大同小异，通常约为10R.”[8]

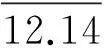
褚鲁统规则不仅仅只是描述沸点物理特性的经验规则，同时也可以是由式(3),在理论上准确计算论证的物理定律.

6熔点——冰升华热与熔解热的数值计算

6.1冰升华热的数学公式

将饱和蒸汽压下单元液体的玻尔兹曼因子方程[4]直接改写为描述冰与饱和蒸汽平衡体系的玻尔兹曼因子方程

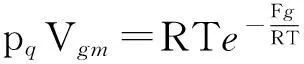
(4)

其中pq为冰的饱和蒸汽压; Vgm为冰的摩尔体积;Fg为冰的摩尔表面自由能，数值上等于摩尔分子穿越冰与饱和蒸汽界面升华为蒸汽分子过程中,克服冰表面的保守力作用所做的功.

由式(4)可直接导出冰与饱和蒸汽界面的表面特性函数：

(1)摩尔表面自由能方程

Fg=RT(lnR+lnT-lnpq-lnVgm)

(5)

(2)摩尔表面熵方程

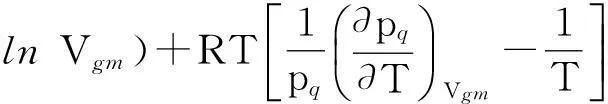
(6)

(3)摩尔表面能方程

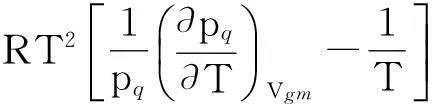
(7)

(4)摩尔升华焓方程

Hg=ug+pq(Vqm-Vgm)=

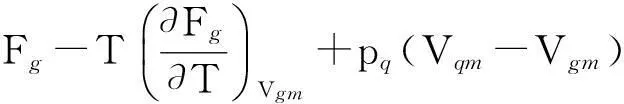
(8)

式(5)～(8)在可实验实测的宏观特性参量pq,Vqm,Vgm,T与不可实验实测的液体表面特性函数Fg,Sg,ug,Hg之间架起了衔接的桥梁；为定量计算表面热力学函数及其相关的物理量打开了方便之门.例如,从摩尔升华焓方程式(8)出发即可得到升华热的数学表达式

(9)

6.2冰升华热的数值计算

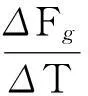
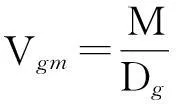
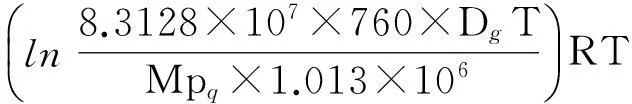
(10)

由物理手册查得温度为-2℃与0℃冰的实验观测数据[9]为

pq-2=3.879mmHg

pq0= 4.579mmHg

Dg-2≈ Dg0= 0.9g/cm3

将上列观测数据代入式(10) 计算,即可得到

Fg-2=

1.985 9×271.15 =6 618.44cal/mol

1.9859×273.15 =6581.25cal/mol

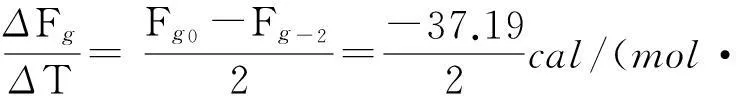
-18.595cal/(mol·℃)

(2) 理论计算升华热λg0

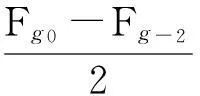
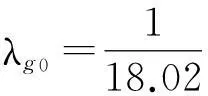
273.15×1.9859)cal/g=677.19cal/g

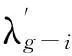
79.72cal/g+597.40cal/g=677.12cal/g

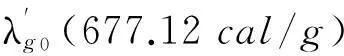
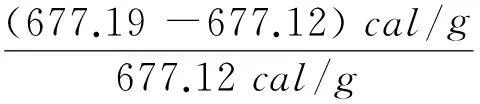
6.3冰熔解热的数值计算

参考文献由[3]表1查得:0 ℃时水气化热的纯理论计算值为λi-q(599.96 cal/g)[3]. 可以用0 ℃时冰升华热的纯理论计算值λg0与0 ℃时水气化热的纯理论计算值λi-q的差来计算0 ℃时冰熔解热的纯理论计算值λg-i,即

λg-i=λg0-λi-q=

677.19cal/g-599.96cal/g=77.23cal/g

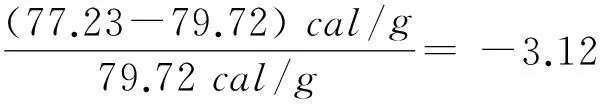
应用冰与饱和蒸汽平衡体系的玻尔兹曼因子方程式(4), 不仅可以对冰的升华热与熔解热进行纯理论的数值计算, 而且计算结果与实验观测值都吻合得很好.

7结论

应用气体、液体与冰的玻尔兹曼因子方程, 对自然界物质在“临界点、沸点、熔点”时的物理特性进行数值计算,理论计算结果与实验观测值高度吻合.事实表明:

(1)简明的数学语言可以在很宽的温度范围内准确描述自然界物质物态变化的客观规律;

(2)玻尔兹曼因子方程是更具普适性的物态方程.

参 考 文 献

1杨振宁.相变与临界现象的引论性评注.戴定国译.低温与超导,1985(1):76

2汤文辉,张若棋.物态方程理论及计算概论(第2版).北京:高等教育出版社,2008. 13

3吴义彬.汽化热与沸点汽化熵的理论计算.物理通报,2013(7):90

4吴义彬．饱和蒸汽压下单元液体的物态方程及其应用.江西科学,2010,28(5):593

5吴义彬．实际气体的玻尔兹曼因子方程.江西科学,2011,29(1):11

6(美)卡尔L·约斯.MATHESON气体数据手册(第1版).陶鹏万，黄建彬，朱大方译.北京：化学工业出版社，2003

7钱尚武，章立源，李椿. 热学(第2版).北京：高等教育出版社，2008.272

8唐有祺. 统计力学及其在物理化学中的应用.北京：科学出版社，1979. 474

9(前苏) К·П·雅阔夫列夫主编.简明物理技术手册第一卷.黄镜权,尤烈之译 .北京：中国工业出版社,1966.446,389

10王竹溪.热力学(第2版).北京: 北京大学出版社,2005. 161

TheNumericalCalculationofCharacteristicsof

CriticalPoint,BoilingPointandMeltingPoint

ApplyingBoltzmannFactorEquation

WuYibin

(NanchangSeniorScientistsandTechnologistsAssociation,Nanchang,Jiangxi330003)

Abstract:By applying Boltzmann factor equation of gas, liquid, and ice, the physical characteristics of “critical point, boiling point, and melting point” of nature matter were numerically calculated and the results were highly consistent with the observed values. It is proved that the concise mathematical language is capable of describing the objective rules of change of nature matters or state within a wide temperature range. The Boltzmann factor equation is the state equation that has more universality.

Keywords:Boltzmannfactorequation;criticalpoint;boilingpoint;meltingpoint;physicalcharacteristics