突破带电粒子问题的两种思路与两种方法

突破带电粒子问题的两种思路与两种方法

辉志文

(凤庆一中云南 临沧675900)

收稿日期：(2015-02-25)

带电粒子在磁场中运动的问题，是高中物理学习的重点，对学生的空间想象能力、物理过程的分析能力以及物理规律的综合应用能力都有很高的要求.尤其是临界问题，粒子的运动轨迹往往是一个残缺圆，因此会出现一系列最值.由于此类问题综合性强，思维能力要求较高，具有很强的选拔功能，因此成为历年高考的热点.笔者在实际教学中做了两种方法和两种思路突破尝试，仅供各位同仁参考.

1确定半径的两种方法

方法1:已知磁感应强度和入射速度，直接用洛伦兹力提供向心力计算.

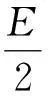
(1)粒子在Ⅱ区域匀强磁场中运动的轨迹半径；

(2)O，M间的距离；

(3)粒子从M点出发到第二次通过CD边界所经历的时间．

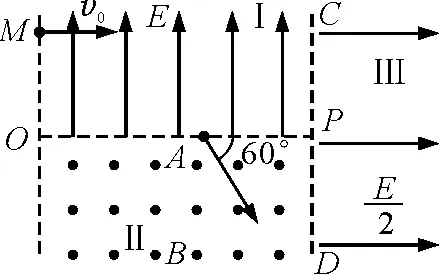
图1

解析：(1)如图2所示，从M到A的过程中，粒子做类平抛运动，则

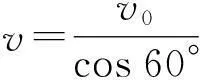
由洛伦兹力提供向心力

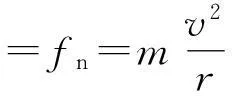
可得

(2)、(3)略.

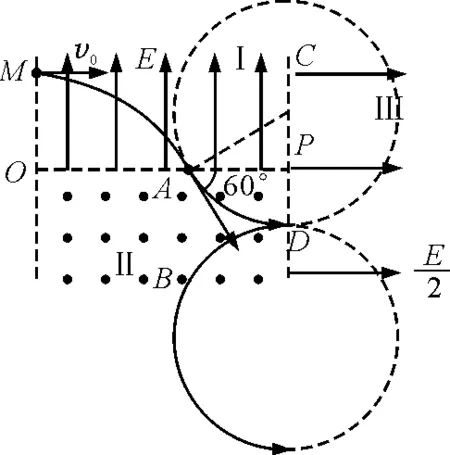
图2

方法2:已知某段距离，磁感应强度或者入射速度未知，构建直角三角形，用几何关系求解.

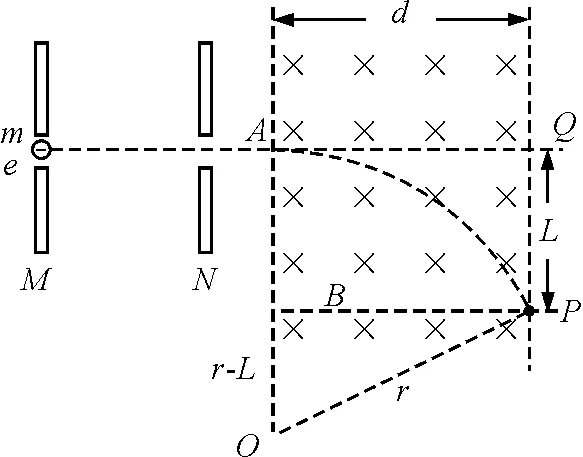
图3

【例2】如图3所示，电子自静止开始经M，N板间(两板间的电压为U)的电场加速后,从A点垂直于磁场边界射入宽度为d的匀强磁场中，电子离开磁场时的位置P偏离入射方向的距离为L，如图所示．求:匀强磁场的磁感应强度．(已知电子的质量为m，电荷量为e)

解析：设电子经加速电场加速后速度为v0，则

可得

由几何关系得

d2+(r-L)2=r2

可得

洛伦兹力提供向心力

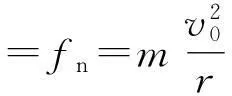
则

2动态问题两种思路

思路1:已知磁感应强度B和速度的方向，不知道速度的大小，或者已知速度，磁感应强度B大小未知，运动轨迹是一簇圆心共线、大小不等的内切圆，即通过改变圆的大小找临界条件.

【例3】如图4所示，一带电微粒质量m=2.0×10-11kg,电荷量q=+1.0×10-5C，从静止开始经电压U1=100 V的电场加速后，水平进入两平行金属板间的偏转电场中，微粒射出电场时的偏转角θ=30°，并接着进入一个方向垂直纸面向里、宽度D=34.6 cm的匀强磁场区域.已知偏转电场中金属板长L=20 cm，两板间距d=17.3 cm，重力忽略不计.求：

(1)带电微粒进入偏转电场时的速率v1；

(2)偏转电场中两金属板间的电压U2；

(3)为使带电微粒不会由磁场右边射出，该匀强磁场的磁感应强度B至少多大.

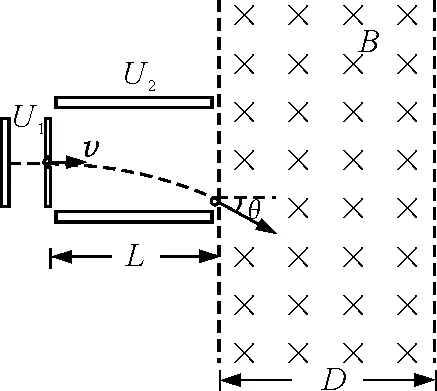
图4

分析：如图5所示，通过作图可以看到,随着v0的增大，圆半径增大，临界状态就是圆与右边界相切.

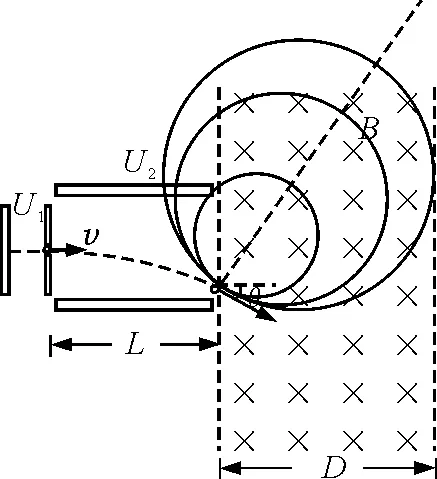
图5

类似还有图6几种情况.

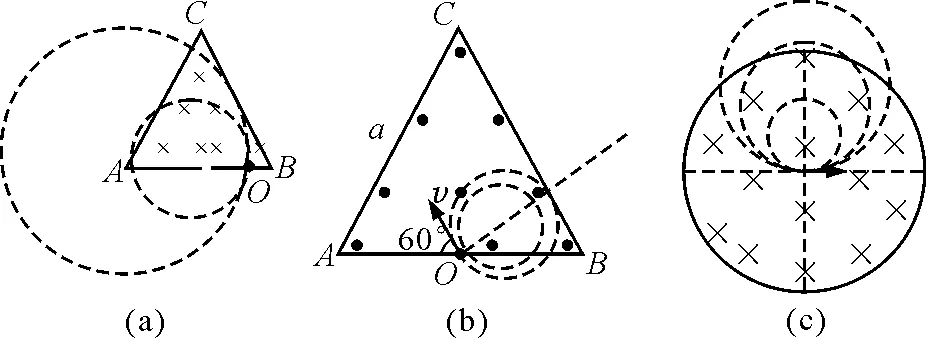
图6

思路2:磁感应强度和速度大小已知，速度方向具有任意性，以入射点为固定点，将运动轨迹圆旋转一周找临界条件.

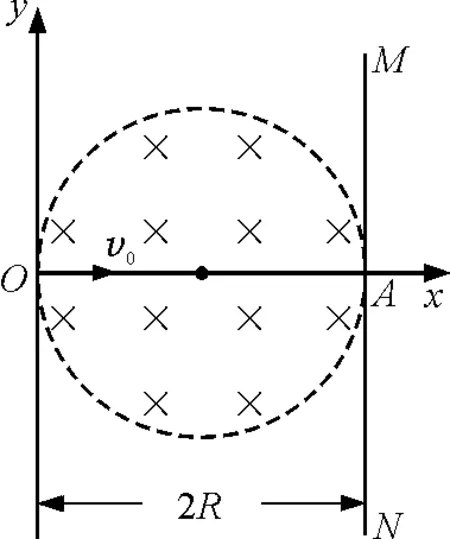
图7

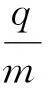
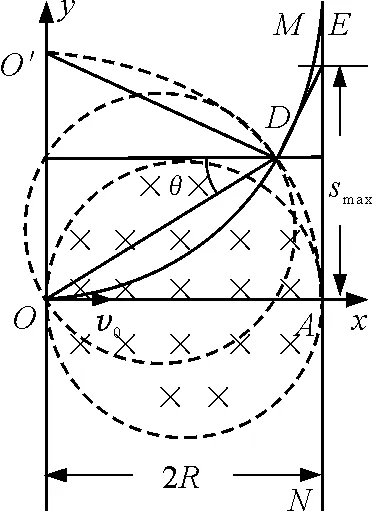
图8

【例5】电子质量为m，电荷量为e，从坐标原点O处沿xOy平面射入第一象限，射入时速度方向不同，速度大小均为v0，如图9所示.现在某一区域加一方向向外且垂直于xOy平面的匀强磁场，磁感应强度为B，若这些电子穿过磁场后都能垂直射到荧光屏MN上，荧光屏与y轴平行，求：

(1)荧光屏上光斑的长度；

(2)所加磁场范围的最小面积.

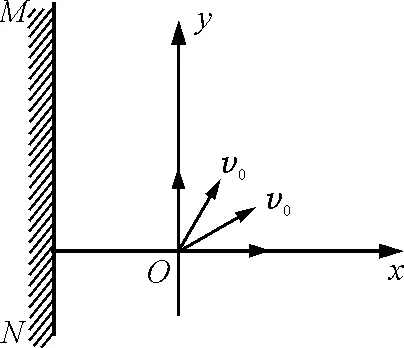
图9

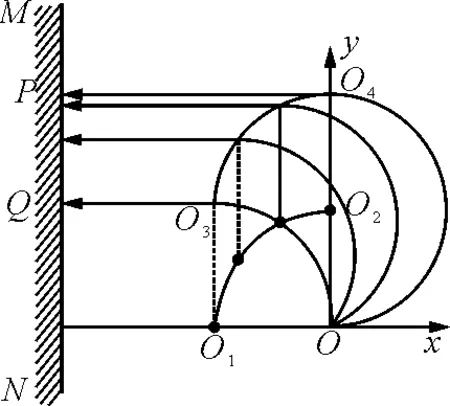
图10

若改为“磁场方向垂直于xOy平面向里，荧光屏MN移至y轴右侧”，其他条件不变，情况又怎样呢？(所加磁场的最小范围为一“树叶”形状,如图11所示)

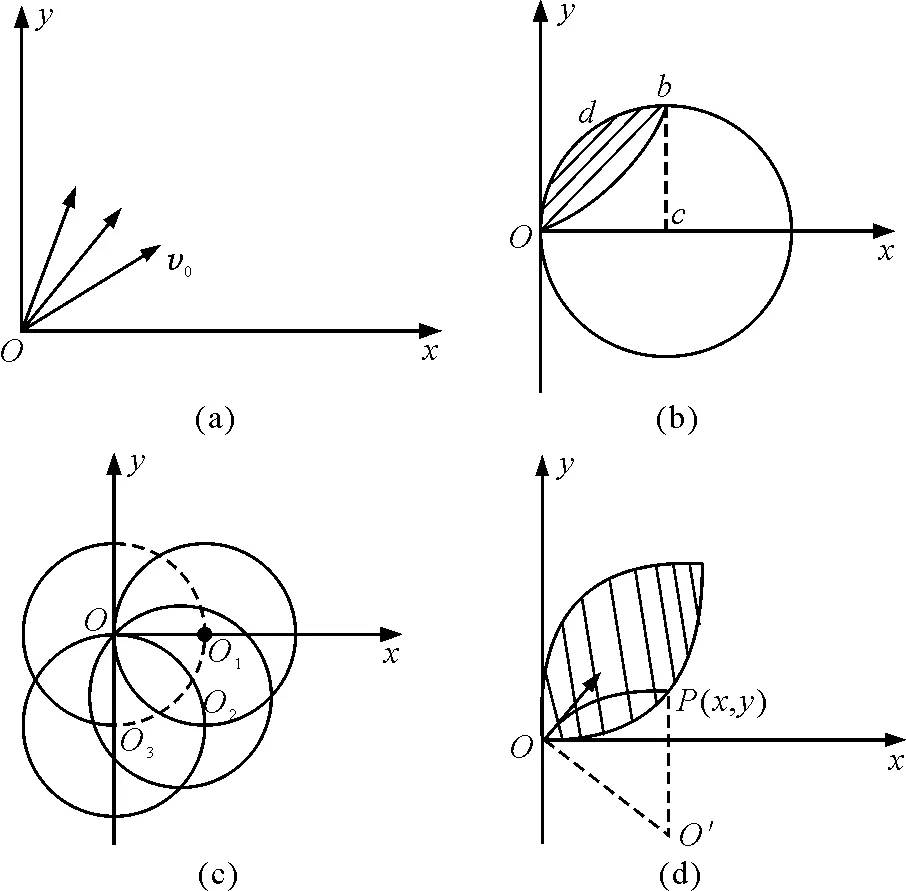
图11

综合以上题型，我们可以看到，这些问题的解答要求学生有较高分析思维能力以及想象能力，这需要在平时的复习中让学生涉猎一些有代表性的习题，这样才能使学生在高考应试中得心就手，应对自如.

参 考 文 献

1王良调.联想解题 高中物理.吉林：吉林人民出版社，2000.750～752

2胡开文.北大考典(物理).北京：北京大学出版社， 2005.76～77

3陈宜生.大学物理(上册) .天津：天津大学出版社，1999.61～63