模拟训练(八)
2016-01-06
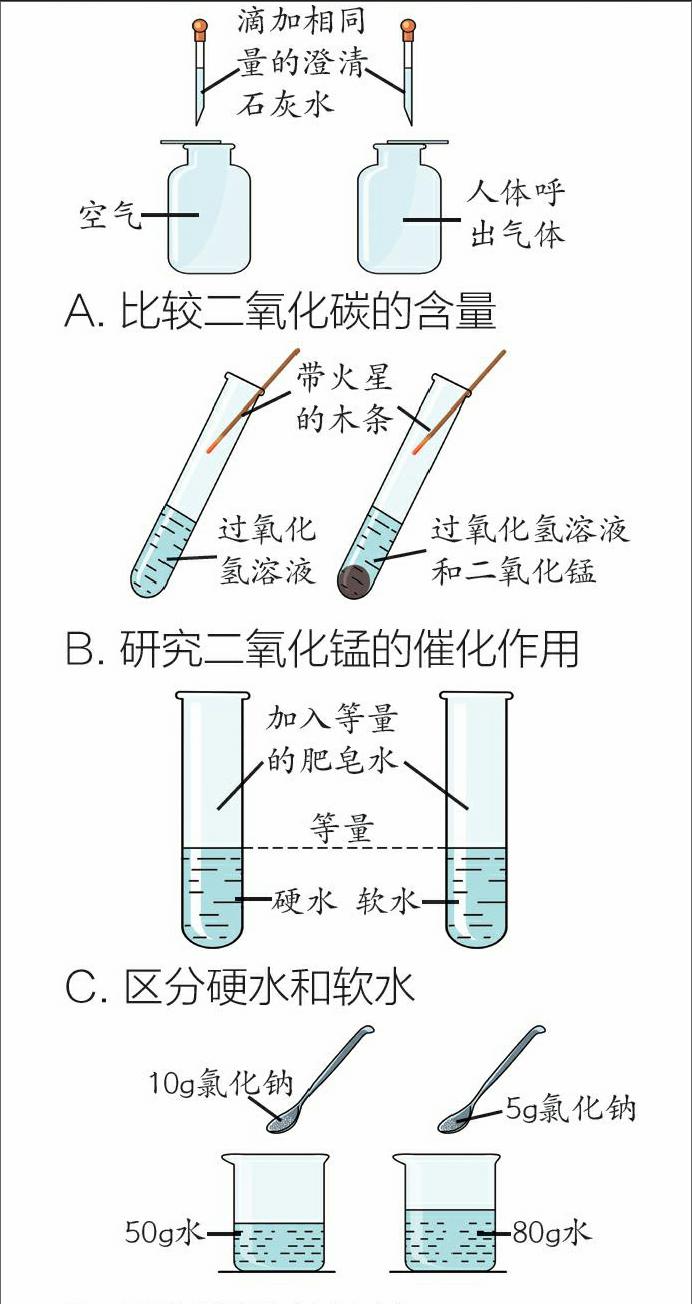
1. 下列实验方案的设计中,没有正确体现“对比”这一科学思想的是( )。
A. 比较二氧化碳的含量
B. 研究二氧化锰的催化作用
C. 区分硬水和软水
D. 配制氯化钠溶液
2. 碳酸氢钠又称小苏打,它是生活中常见的一种盐。下列有关小苏打的说法中错误的是( )。
A. 发酵粉中含有碳酸氢钠,能使焙制出的糕点疏松多孔
B. 干粉灭火器中含有碳酸氢钠,可用来扑灭油、气燃烧引起的火灾
C. 碳酸氢钠和柠檬酸、水等混合可制成汽水
D. 碳酸氢钠不能用作治疗胃酸过多的药剂
3. 有关下列实验现象的叙述中错误的是( )。
A. 硫在氧气中燃烧产生蓝紫色的火焰
B. 铁在氧气中燃烧时,火星四射,放出大量的热,生成黑色固体
C. 镁在空气中燃烧时发出耀眼的白光,生成的氧化镁为白色固体
D. 氢氧化钠固体溶于水时有明显的吸热现象
4. SO2和Cl2均有毒有害,在实验室里做实验时,可将两者同时通入水中,会生成两种酸,发生的反应为:SO2 + Cl2 + 2H2O → 2HCl +(另一种酸),其中另一种酸的化学式是______;向该酸液中投入锌粉会见到大量气泡,此时发生的反应属于________(填写基本反应类型)反应。为了检验上述吸收液中的两种酸,可以先加足量______(填写化学式)试液,然后过滤,在滤液中再加 ______(填写化学式)试液。
5. 燃油、燃气助动车(俗称两用车)使用时会产生较多尾气,严重污染城市生态环境。据有关专家介绍,每辆两用车产生的有害尾气已经超过小汽车的排放量。某同学通过查阅资料,发现两用车尾气中含有CO2、CO、SO2、氮氧化物、挥发性有机物、固体颗粒等物质。由此,该同学推测:燃气中含有碳以及少量的氮、硫等物质,燃气在燃烧过程中发生了如下化学反应:
2C + O2=2CO(不完全燃烧)
C + O2=CO2(完全燃烧)
S + O2=SO2
N2 + O2=2NO
(1)该同学的推测____(填“正确”或“不正确”)。理由是:__________。
(2)请提出一条用化学手段治理汽车尾气的合理化建议:_______________。
(适合初中学生)
6. 在注射器中放入适量的NO2,推、拉注射器活塞会发生反应:2NO2 N2O4 + Q。当达到平衡时,若分别单独改变下列一个条件,重新达到平衡后,能使混合气体平均分子量增大的是( )。
A. 通入N2(总体积不变)
B. 推压注射器活塞
C. 升高温度
D. 降低温度
7. 宜兴的紫砂制品很珍贵,以下有关说法中错误的是( )。
A. 紫砂的材料是一种特殊矿产(宜兴紫泥),它含有较多铁质,呈紫色,紫泥矿层很薄,非常宝贵
B. 紫泥做成茶壶坯后还需要在其内侧施釉,以防渗水
C. 紫砂茶壶使用之前,不要用化学洗涤剂清洗,因为紫砂茶壶有透气性和吸收性,会吸收洗涤剂的怪味,致使以后泡的茶味不纯
D. 普通的砂锅属陶器,而紫砂茶壶属瓷器
8. 磷化氢(PH3)又称为膦,常温下,膦是无色的有毒有味气体。膦分子的空间构型和氨分子相似,为三角锥形。以下关于PH3的叙述中正确的是( )。
A. PH3是极性分子
B. PH3在水中的溶解度(水溶性)与NH3相似
C. PH3分子中有未成键的电子对
D. PH3分子中的P-H键是非极性键
9. 氯化亚砜(SOCl2)在常温下是一种无色液体,沸点79℃,是一种重要的有机试剂,用于将ROH转化为RCl。氯化亚砜遇水分解,故常需在无水条件下使用。
(1)试写出它与水完全反应的化学方程式(提示:产物只生成两种化合物,其摩尔比为1∶2):________;
(2)设计一些简单的实验来验证上述化学方程式是正确的(只需给出实验方法和原理,无需描述实验仪器和操作):________________。
(适合高中学生)
2015年第 8 期答案
1. C 2. D 3. B
4. (1)原因一是水放得太少了,二氧化碳不能完全溶解,改进方法是:改用碱性水如洗衣粉水溶液、肥皂水等;原因二是蜡烛在氧气没耗尽时就熄掉了,即蜡烛除氧气效果不好,改进方法是:改用红磷或白磷等(答案合理即可)
(2)原因一是烧杯杯口朝下垂直倒扣的速度太慢,使烧杯内充入过多灼热的气体,改进方法是: 烧杯倒扣的速度要快;原因二是烧杯杯口没有垂直倒扣,而斜扣时会流入不少水,改进方法是:烧杯杯口必须是垂直倒扣(答案合理即可)
5. B 6. B
7. (1)84消毒液呈碱性,使茶水的pH值上升,茶水遇碱性颜色变深;84消毒液有漂白作用
(2)84消毒液凭其强氧化性杀菌褪色,鞣酸铁中铁为+3价,无法再氧化,故不能褪色
(3)草酸和三价铁发生配位反应,生成三草酸合铁(Ⅲ)离子[Fe(C2O4)3]3-
8.(1)估计这些黑色物质是超细的铝末
(2)取黑色颗粒和黑色泡沫用水洗净,过滤,置于试管中,加过量1∶1盐酸,如能产生可燃性气体(氢气)并黑色颗粒全部消失,即可证明假设正确
