众里寻他千百度——对内含两圆切接三角形存在性的探索

众里寻他千百度——对内含两圆切接三角形存在性的探索

●金竹明(洛舍镇中心学校浙江德清313218)

我们知道，等边三角形每个角的内角平分线、对边上的中线、对边上的高线都互相重合，即每条边上都三线合一．因为三角形的内心是3个内角平分线的交点，外心是3条边中垂线的交点，所以等边三角形的内心与外心重合，即等边三角形的内切圆与外接圆是同心圆．笔者在教授了三角形的内切圆的新课后，在课后练习中碰到了一个习题：

若△ABC的内切圆和外接圆是2个同心圆，则△ABC一定是

()

A．等边三角形B．等腰三角形

C．直角三角形D．钝角三角形

因为等边三角形内切圆与外接圆是同心圆，所以根据直觉答案应选A．由于三角形的内心在三角形的内部，而直角三角形的外心在其斜边的中点，不可能与三角形内部的内心重合；钝角三角形的外心在三角形的外部，也不可能与三角形的内心重合；等腰三角形包括等腰直角三角形，其内心与外心不能重合.因此可依次排除选项C，D，B，正确答案只能选A．这个选择题是用排除法解决了，但除等边三角形外的其他三角形的内心与外心是否都不能重合？由此，笔者展开了以下的探究之旅．

显然，任意一个确定的三角形必有唯一的内切圆和唯一的外接圆.任何一个三角形的内切圆与其外接圆的位置关系只能是内含，因此内含两圆中可能存在一个三角形，这个三角形既是小圆的外切三角形，又是大圆的内接三角形.以下为了说明的方便，我们不妨定义：如果内含两圆中小圆的外切三角形又是大圆的内接三角形，那么称这个三角形为内含两圆的切接三角形，简称切接三角形．不妨规定三角形的外接圆、内切圆半径分别为R，r，△ABC的边BC，AC，AB所对边长分别为a，b，c．

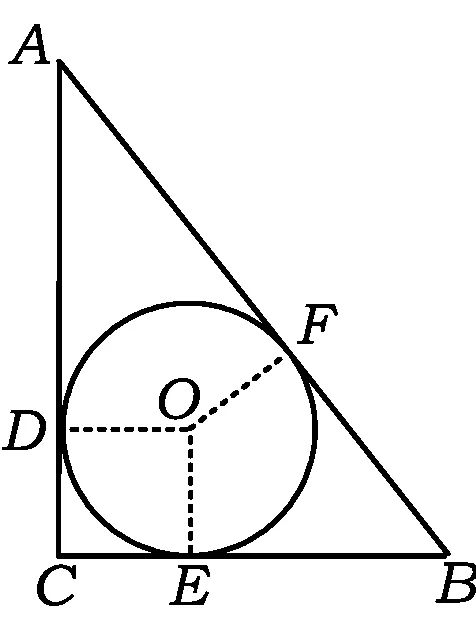
图1

1直角三角形

1．1内切圆半径

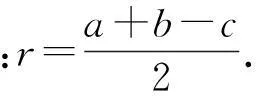
证明联结OD，OE，OF，则

OD⊥AC，OE⊥BC，OF⊥AB．

因为∠C=90°，所以四边形ODCE为矩形.又因为OD=OE=r，所以矩形ODCE为正方形，从而

CD=CE=r，

因此AD=AC-CD=b-r，BE=BC-CE=a-r.

由切线长定理可得

AF=AD=b-r，BF=BE=a-r，

从而AB=AF+BF=b-r+a-r=a+b-2r.

又因为AB=c，所以

c=a+b-2r，

故

1.2外接圆半径

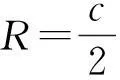
2等腰三角形

2.1等边三角形

2.1.1内切圆半径

如图2，边长为a的等边△ABC的3条边BC，AB，AC分别切⊙O于点D，E，F，联结OB，OC，OD，则OB，OC分别平分∠ABC，∠ACB，从而

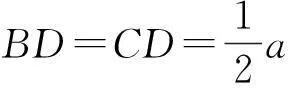
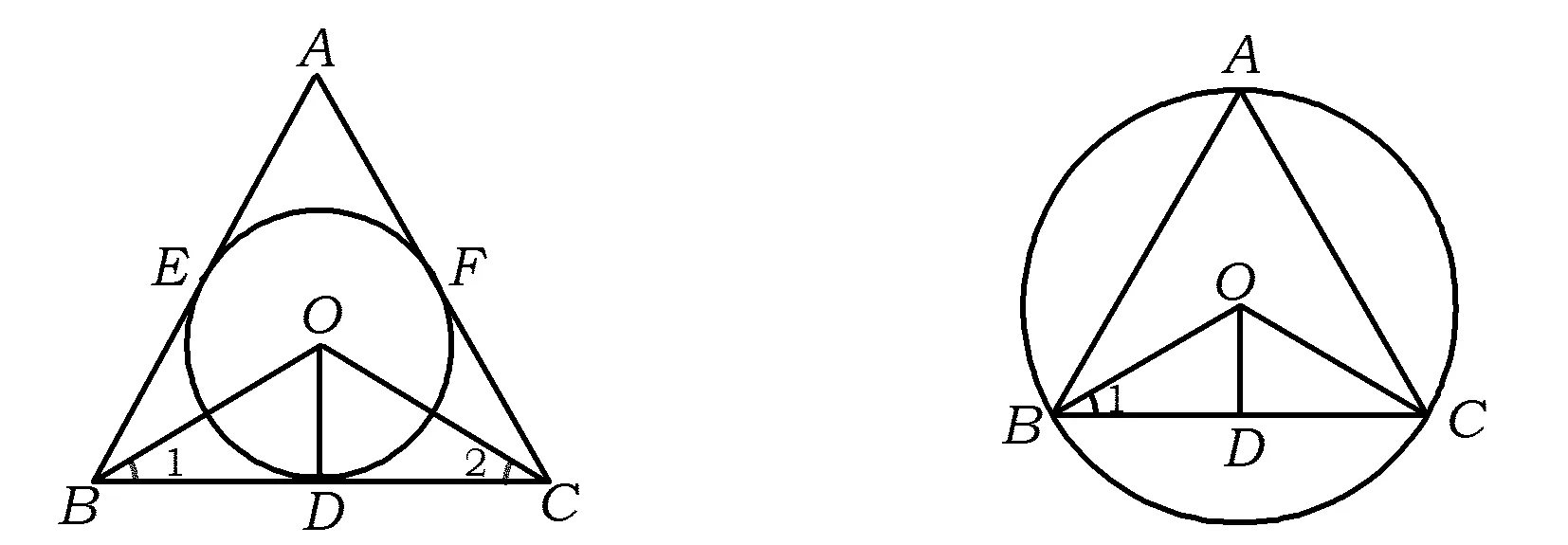
图2 图3

2.1.2外接圆半径

如图3，边长为a的等边△ABC内接于⊙O，联结OB，OC，则OB=OC=R．作OD⊥BC于点D，则

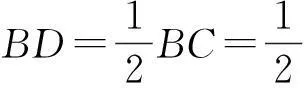
因为∠A=60°，所以∠BOC=120°，从而

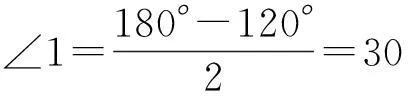
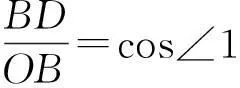
至此可知，等边三角形的内切圆与外接圆是同心圆，且R=2r．

2．2一般等腰三角形

2.2.1内切圆半径

例2如图4，在等腰△ABC中，AB，AC，BC分别切⊙O于点D，E，F．记AB=AC=a，BC=c，求等腰△ABC的内切圆半径r．

解联结OB，OD，OF，OA,则OD⊥AB，OF⊥BC.由圆和等腰三角形的轴对称性知点A，O，F共线，从而AF⊥BC，于是

BF2+AF2=AB2，

即

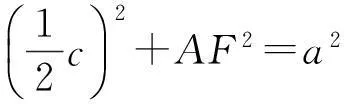
从而

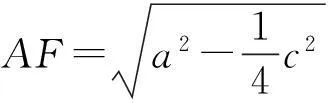
故

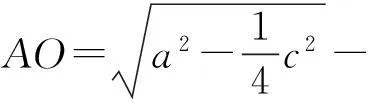
因为

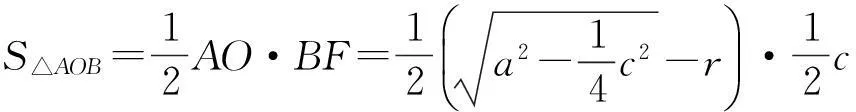
所以

故

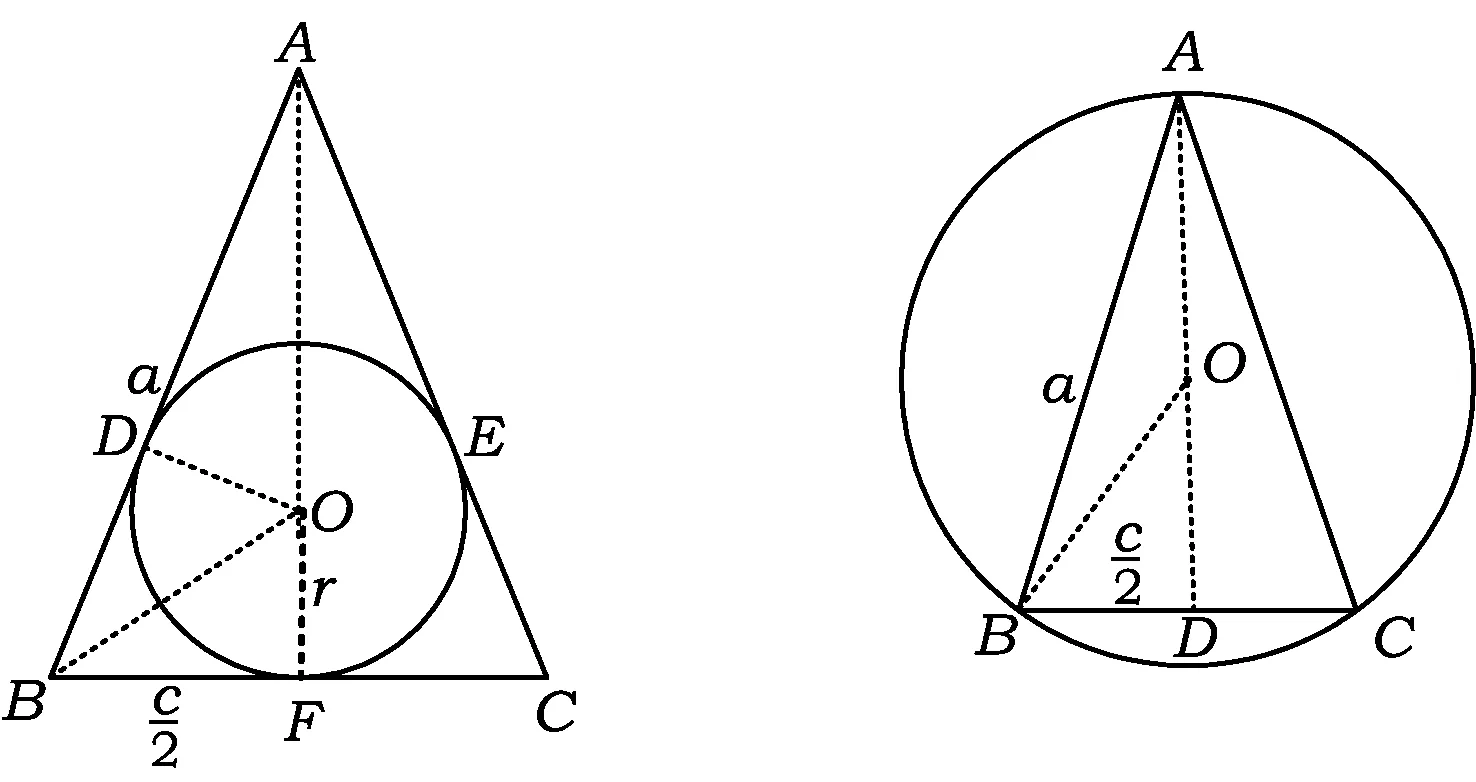
图4 图5

2.2.2外接圆半径

例3如图5，等腰△ABC内接于⊙O．记AB=AC=a，BC=c,求△ABC的外接圆半径R．

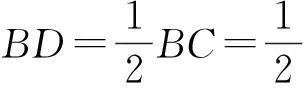
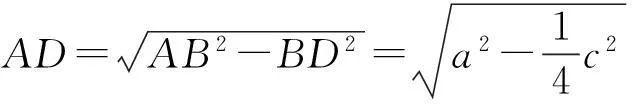
从而

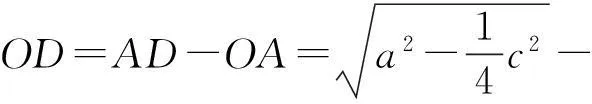
在Rt△BOD中,

BD2+OD2=OB2，

即

从而

3一般三角形

3.1内切圆半径

例4如图6，△ABC的3条边切其内切圆⊙O于点D，E，F，求△ABC的内切圆半径r．

解联结OD，OE，OF，OA，OB，OC.因为点D，E，F是切点，所以OD⊥AB，OE⊥AC，OF⊥BC，且OD=OE=OF=r，从而

S△ABC=S△BOC+S△AOC+S△AOB=

于是

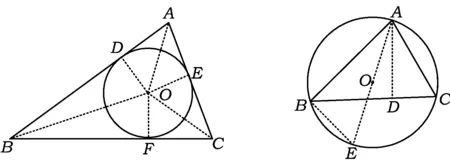
图6 图7

3.2外接圆半径

例5如图7，已知⊙O是△ABC的外接圆，求△ABC的外接圆半径．

解作AD⊥BC于点D，联结AO并延长交⊙O于点E，联结BE．因为AE是直径，所以

∠ABE=90°=∠ADC.

又因为∠E=∠C，所以

Rt△ABE∽Rt△ADC，

从而

即

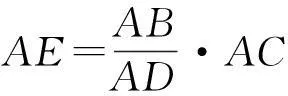
从而

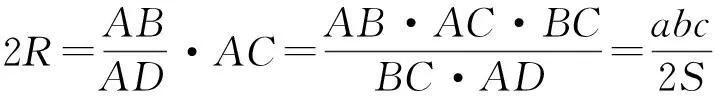
故

类似地，借助海伦公式，我们也能用只含a，b，c的式子表示R，但形式较复杂，不如此式简洁．

3．3任意三角形内外心之间的距离

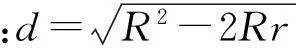
(第4届IMO试题)

证明如图8，联结IO，延长IO，OI分别交⊙O于点E，F．联结CI，并延长CI交⊙O于点G．联结GB，IB，GO，并延长GO交⊙O于点H，联结BH．显然

R2-d2=(R+d)(R-d)=IE·IF,

由相交弦定理可得

IE·IF=IG·IC，

即

R2-d2=IG·IC.

因为I是内心，所以

∠ABI=∠CBI，∠ACI=∠BCI，

从而∠GIB= ∠CBI+∠BCI=∠ABI+∠ACI=

∠ABI+∠GBA=∠GBI，

即

BG=IG.

因为GH是⊙O的直径，所以

∠GBH=∠IDC=90°.

又∠DCI=∠H，从而

Rt△IDC∽Rt△GBH，

于是

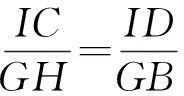
即

IC·GB=ID·GH，

亦即

IC·IG=ID·GH=r·2R=2Rr，

从而

R2-d2=2Rr，

故

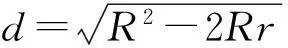
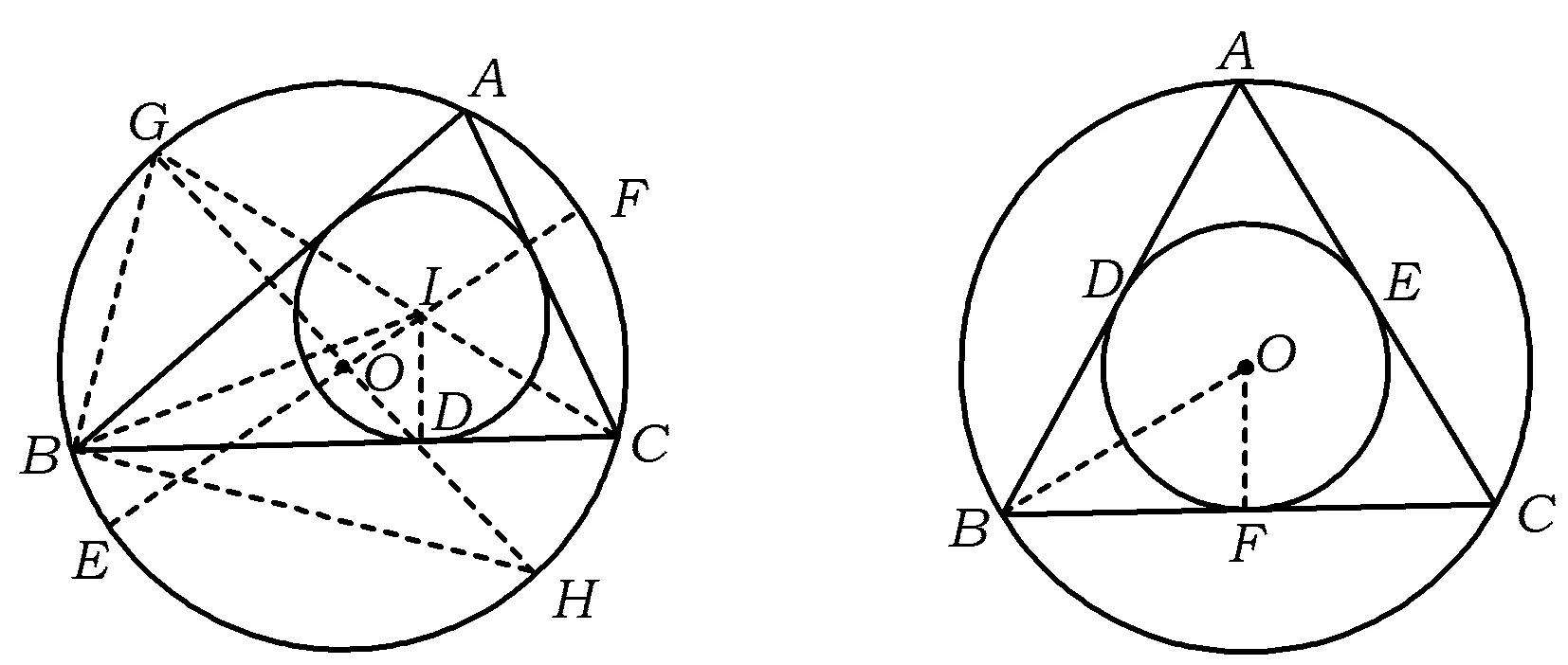
图8 图9

例7如图9,已知△ABC的内切圆与外接圆为同心圆，△ABC的3条边分别切⊙O于点D，E，F,求证：△ABC为等边三角形．

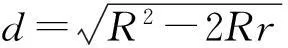
R=2r(R=0舍去),

进而

OB=2OF.

因为OF⊥BC，所以

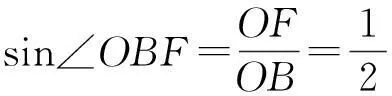
从而

∠OBF=30°.

因为小⊙O内切于△ABC，所以

∠ABC=2∠OBF=2×30°=60°，

同理可得

∠A=∠C=60°，

故△ABC为等边三角形．

证法2联结OD，OE，OF．因为△ABC的3条边与小⊙O相切，所以

OD⊥AB，OE⊥AC，OF⊥BC.

又因为OD=OE=OF，所以AB=BC=AC(同圆中相等的弦心距所对应的弦相等)，因此△ABC为等边三角形．

至此，我们“令人信服”地解决了这个问题，即若一个三角形的内切圆与外接圆是同心圆，则此三角形必为等边三角形，且R=2r．

如果再进一步思考，我们不难联想到以下2个问题：

1)是否任意半径的2个同心圆都存在切接三角形？如果必定存在，其切接三角形是否唯一？如果有条件存在，那么存在的条件是什么？其切接三角形是否唯一？

2)更一般地，内含两圆是否存在切接三角形？如果必定存在，其切接三角形是否唯一？如果有条件存在，那么存在的条件是什么？其切接三角形是否唯一？

似乎第1)个问题简单些，但笔者找不到好的解决办法，于是将视线转到第2)个问题．如果第2)个问题能解决，那么第1)个问题自然容易解决．因为任何一个三角形都有唯一的内切圆和唯一的外接圆，所以内含两圆是可能存在切接三角形的，即内含两圆存在切接三角形是有条件的．估计这个条件与大圆的半径R、小圆的半径r及两圆的圆心距d有关．如何得到这个存在的条件呢？笔者思索良久，没有头绪．后来豁然开朗，考虑到会不会{“d2=}R2-2Rr”就是这个条件呢？即“切接三角形存在”是否成立．笔者进行了多次正面尝试，无功而返，于是尝试用反证法来证明．

图10

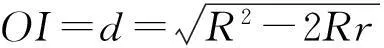
证明假设切接三角形不存在．过点I，O作⊙O的直径MN．过⊙O与MN的交点D作⊙O的切线交⊙I于点A，B，过点A，B分别作⊙O的2条切线AC，BE，交于点P，由圆及过圆外一点的圆的2条切线的轴对称性知，点P必定在MN上．

因为切接三角形不存在，所以点P必不在⊙I与MN的交点处．设PI=t，则PO=t+d，PD=t+{d+}r，ID=d+r，联结AI，则AI=R，联结CO，则{OC⊥}AP，OC=r，从而

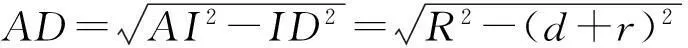
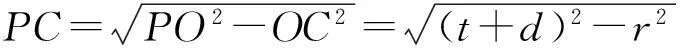
由切线长定理可得

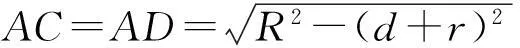
从而AP=AC+PC=

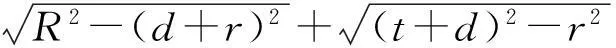
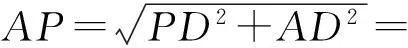
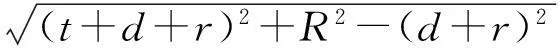
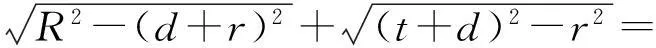
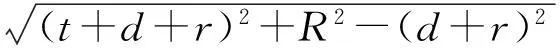
2边平方，并化简整理得

2边再平方，得

[(t+d)2-r2][R2-(d+r)2]=r2(t+d+r)2，

即(t+d-r)[R2-(d+r)2]=r2(t+d+r)，

亦即[R2- (d+r)2-r2]t=

(d+r)r2-(d-r)[R2-(d+r)2]，

从而(R2-d2-2dr-2r2)t=-dR2+d3+d2r+R2r.

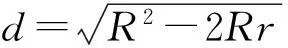
d2=R2-2Rr，

于是(R2-R2+2Rr-2dr-2r2)t=

-dR2+(R2-2Rr)d+(R2-2Rr)r+R2r，

因此

(2Rr-2dr-2r2)t=2R2r-2Rrd-2Rr2.

因为d+r≠R，所以

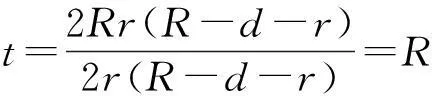
从而点P在⊙I上，即点P就在⊙I与MN的交点处，这与前文所述的“点P必定不在⊙I与MN的交点处”矛盾，因此假设不成立，切接三角形存在，即当内含两圆的圆心距d与两圆半径R，r满足{d2=}R2-2Rr时，必存在切接三角形．这样，我们就证明了当d2=R2-2Rr时，切接三角形的存在性．

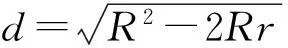
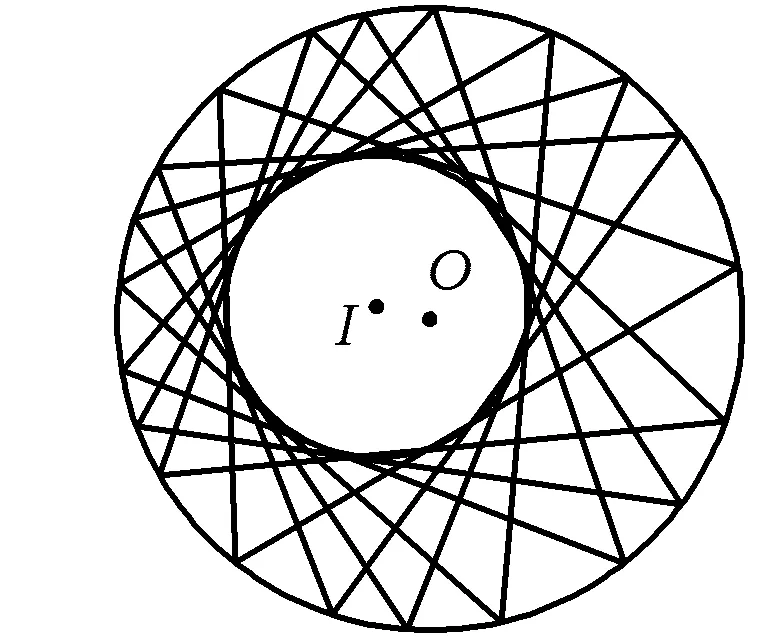
图11

这真是“众里寻他千百度，蓦然回首，那人却在灯火阑珊处”！

事实上，当内含两圆的圆心距d与两圆的半径R，r之间满足d2=R2-2Rr的关系时，其切接三角形必定存在，且有无数个．我们只要过大圆上任意一点作小圆的2条切线，则这2条切线与大圆的2个交点的连线必为小圆的切线(如图11).

虽然笔者暂时还不能证明“无限性”这个美妙的结论，但笔者确信她美丽地存在着．这让笔者真正领略到了数学美的“震撼”性！

数学之美，精妙绝伦，如闻韶乐，如饮甘露，妙趣横生！