一道数学中考题的变式与探究

一道数学中考题的变式与探究

●黄新民(温州市教育教学研究院浙江温州325000)

●刘臻(瓯北街道第一中学浙江永嘉325100)

作为数学教师，每天都要与数学题接触，一些精彩的好题，往往蕴含着丰富的数学思想.在欣赏的同时，有必要对其进行深入地探究.

1原题再现与解析

()

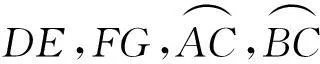
(2015年浙江省温州市数学中考试题)

分析该题以勾股图为背景，引进3个新元素：半圆、MP及NQ，并利用它们之间的内在联系，设置问题.整个设计构思巧妙、新颖，图形美观，题设简洁对称，结构严密，求解过程所用知识均为初中数学核心知识，所用方法也是初中数学重要方法之一——整体思想.这是一个不可多得的好题！

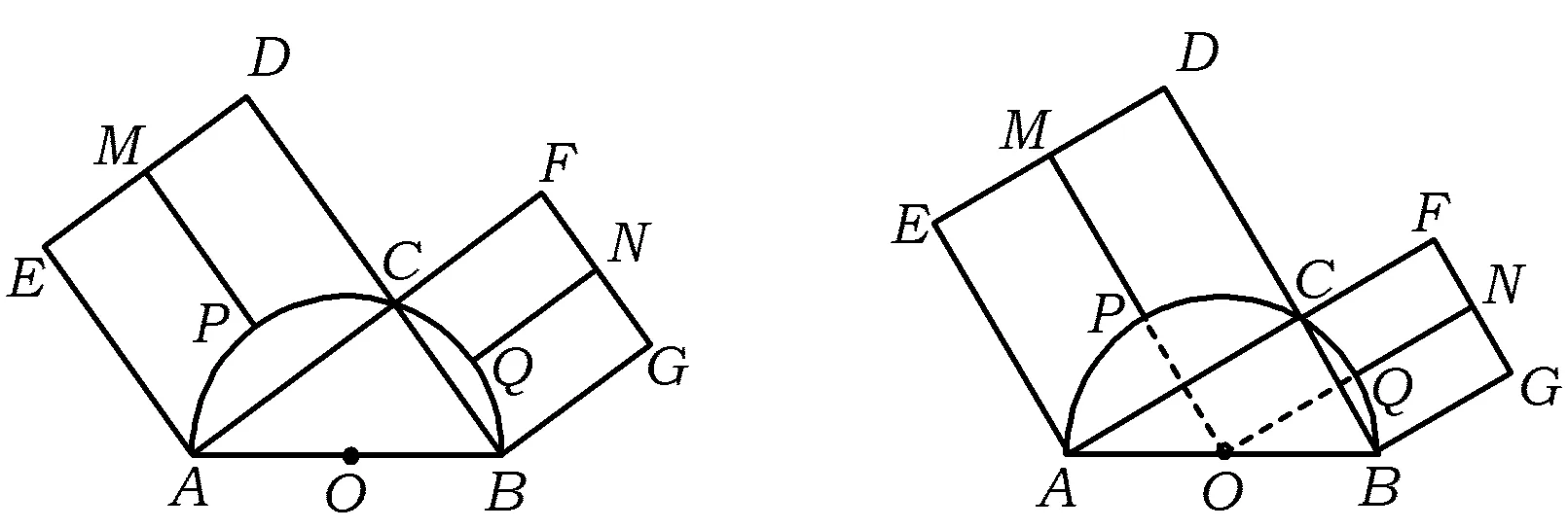
图1 图2

2试题变式与探究

若将原题中“MP+NQ=14，AC+BC=18”这2个条件去掉,则MP-NQ，AC-BC存在以下关系：

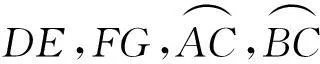
证明如图2，设AC=b，BC=a,圆的半径记为r,则

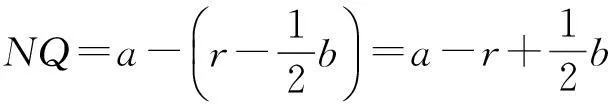
从而

故

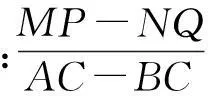
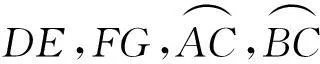
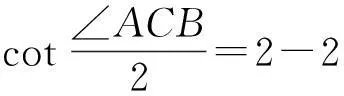
分析数学试题的探究过程遵循从简单到复杂、从特殊到一般的规律.变式分别从具体的数量关系，过渡到了一般的数量关系，并揭示了2种几何对象：数量关系(线段)与位置关系(角度)之间的内在依存和转化关系.这就要求教师平时在教学过程中，要有意识地引导学生去探究几何图形在一般位置关系下的特殊数量关系，也就是几何不变量.

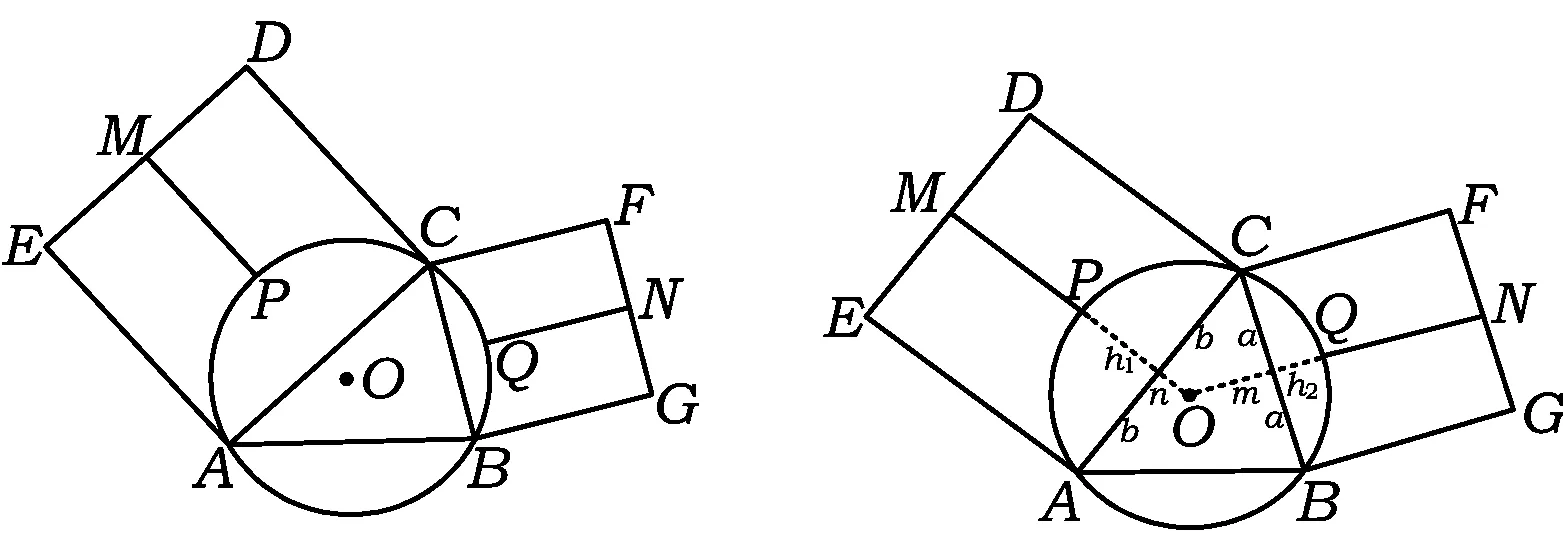
图3 图4

引入一些记号，如图4，设AC=2b,BC=2a，设AC,BC的弦心距分别为n，m，设弓形APC，BQC的高分别是h1，h2，并设圆的半径为r.

引理1结论中的k<1.

证明如图4，不妨设AC>BC，即b>a，于是h1>h2.又h1=2b-MP,h2=2a-NQ，得

2b-MP>2a-NQ，

从而

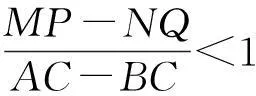
即

k<1.

引理2结论中的k满足关系：

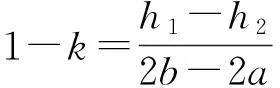
引理3结论中的∠ACB满足关系：

图5

因为OM⊥AB，MH⊥AC,∠ALH=∠BLM,所以

∠BAC=∠M,

从而

BC=EF,

故

OG=OK,KQ=PG.

因为MF为直径，所以∠FEM=90°.又{∠MHC=}∠OTH=90°,从而四边形EHTG为矩形，因此EH=GT=OG-OT=OK-OT=m-n,即

AH=AT-HT=AT-EG=AT-BK=b-a,

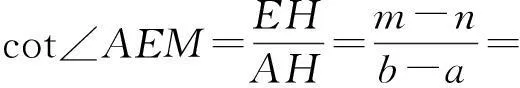
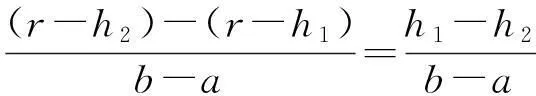
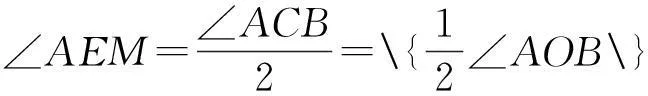
因此

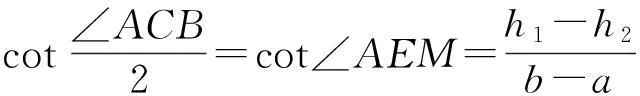
结论的证明由引理2和引理3可得

即结论成立.

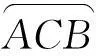
3结论应用与创新

应用该结论，还可以编出许多新题：

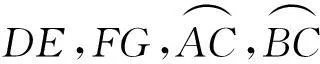
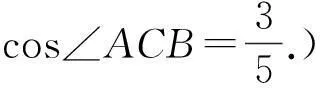
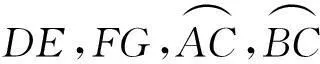
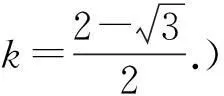
分析新题1与新题2分别从正反2个互逆的角度运用了结论.一方面体现了该结论的实用价值，另一方面也揭示了命题的一个常用方法——赋值法.

一个好的数学试题，可以在检测学生的数学思维过程中起到事半功倍的效果.而对试题进行变式和探究，更是教师在课堂之外应该潜心专研的内容，这将有助于我们更加深刻地理解问题，发现问题本质，从而为促进更高效的数学课堂打下坚实的基础.