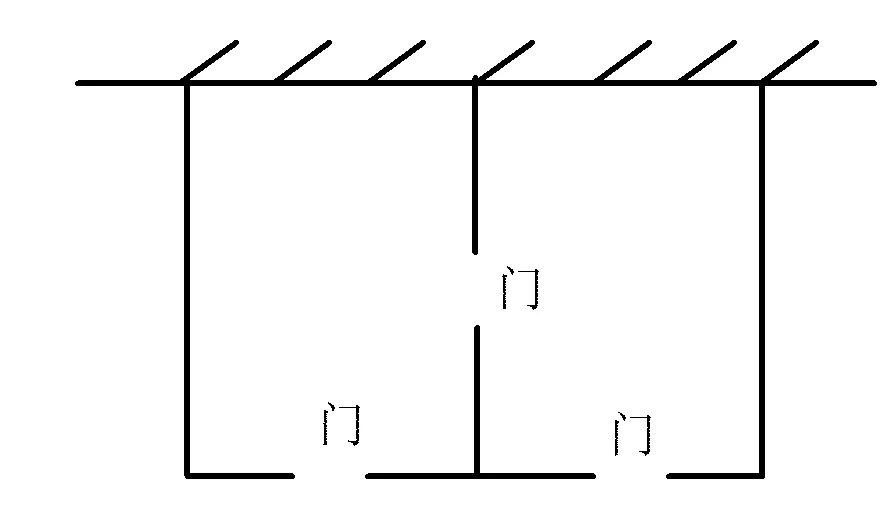
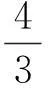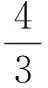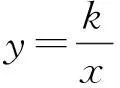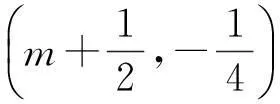注重试题改编 提升思维品质

注重试题改编提升思维品质

●沈国(三合中心学校浙江德清313200)

试题改编是对原有试题进行改造，使之从形式上、考查功能上发生改变而成为新题.常用的方法有：题型的转换、条件与结论的转换、试题背景的转换、静态与动态的转换等.数学思维在思维科学中具有极其特殊的重要地位.数学的教学几乎无时无刻不在引导学生进行思维活动，而试题改编教学对思维品质的培养尤为重要.因此，“研究试题改编，从而提升数学思维的品质”对于形成完善的数学思维结构和发展数学思维能力具有重要的意义.

1试题改编与数学思维广阔性的培养

例1关于x的方程mx2+x-m+1=0，有以下3个结论：①当m=0时，方程只有1个实数解；②当m≠0时，方程有2个不等的实数解；③无论m取何值，方程都有1个负数解.其中正确的是______(填序号)(答案：①③)．

(2015年浙江省台州市数学中考试题)

改编2关于x的函数y=mx2+x-m+1(其中x取任意实数)，有以下3个结论：①无论m取何值，函数图像与x轴至少有1个交点；②无论m取何值，函数图像都经过1个固定点；③无论m取何值，当x>0时，函数y随x的增大而增大.其中正确的是______(填序号)(答案：①②)．

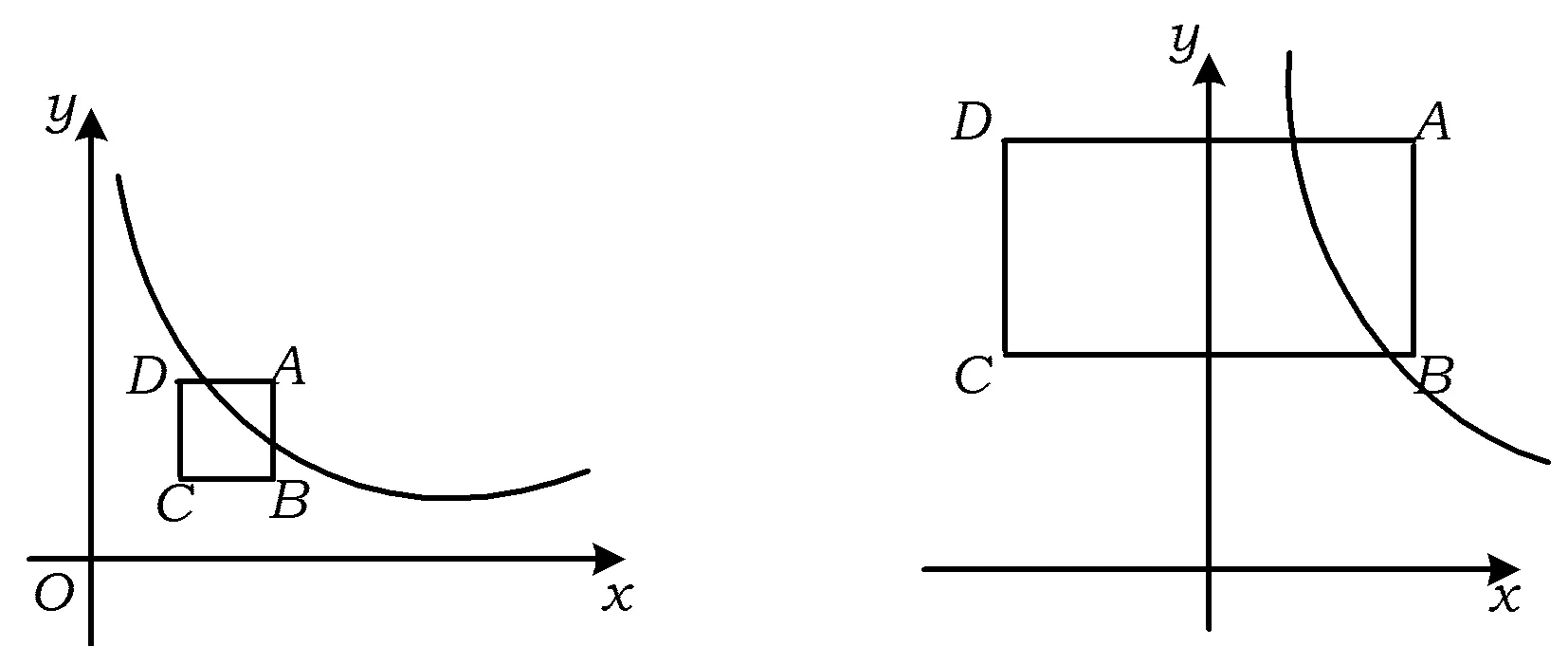
改编意图分式方程与整式方程紧密联系在一起，且分式方程中增根的问题能培养学生的思维能力.抛物线与x轴交点的问题实际上就是解一元二次方程.因此，为了能让学生对前后所学的知识产生联系，完善庞大的数学知识结构，同时培养学生数形结合的思想，一元二次方程的问题都可以进行类似改编，以此来拓宽学生的思维，培养数学思维的广阔性.

()

(2015年浙江省金华市数学中考试题)

(答案：C)

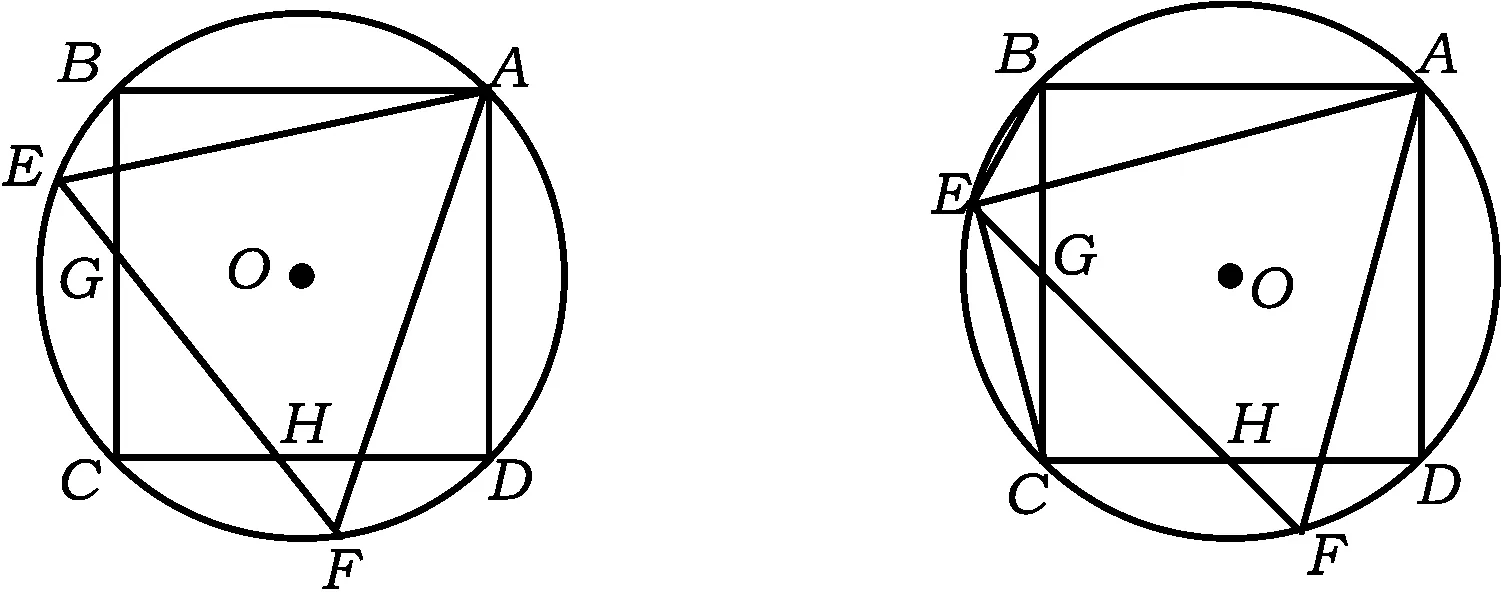
图1 图2

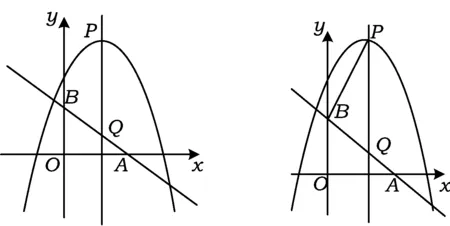
改编如图2，正方形ABCD和正△AEF都内接于⊙O，EF与BC,CD分别相交于点G,H，联结BE,CE，则下列结论错误的是

()

A．CG=BGB．∠ECB=15°

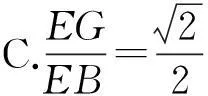
(答案：D)

改编意图原题只解决了一个问题，为了尽可能地发挥试题的功效，全面而深入地考查学生，该题目还可以进一步挖掘.这样不仅用到等边三角形、正方形以及圆的一些特殊性质，还可以用相似、三角函数等知识去解决，全面考查学生的数学知识，以及各种不同思路的掌握程度，培养学生思维的广阔性.

2试题改编与数学思维深刻性的培养

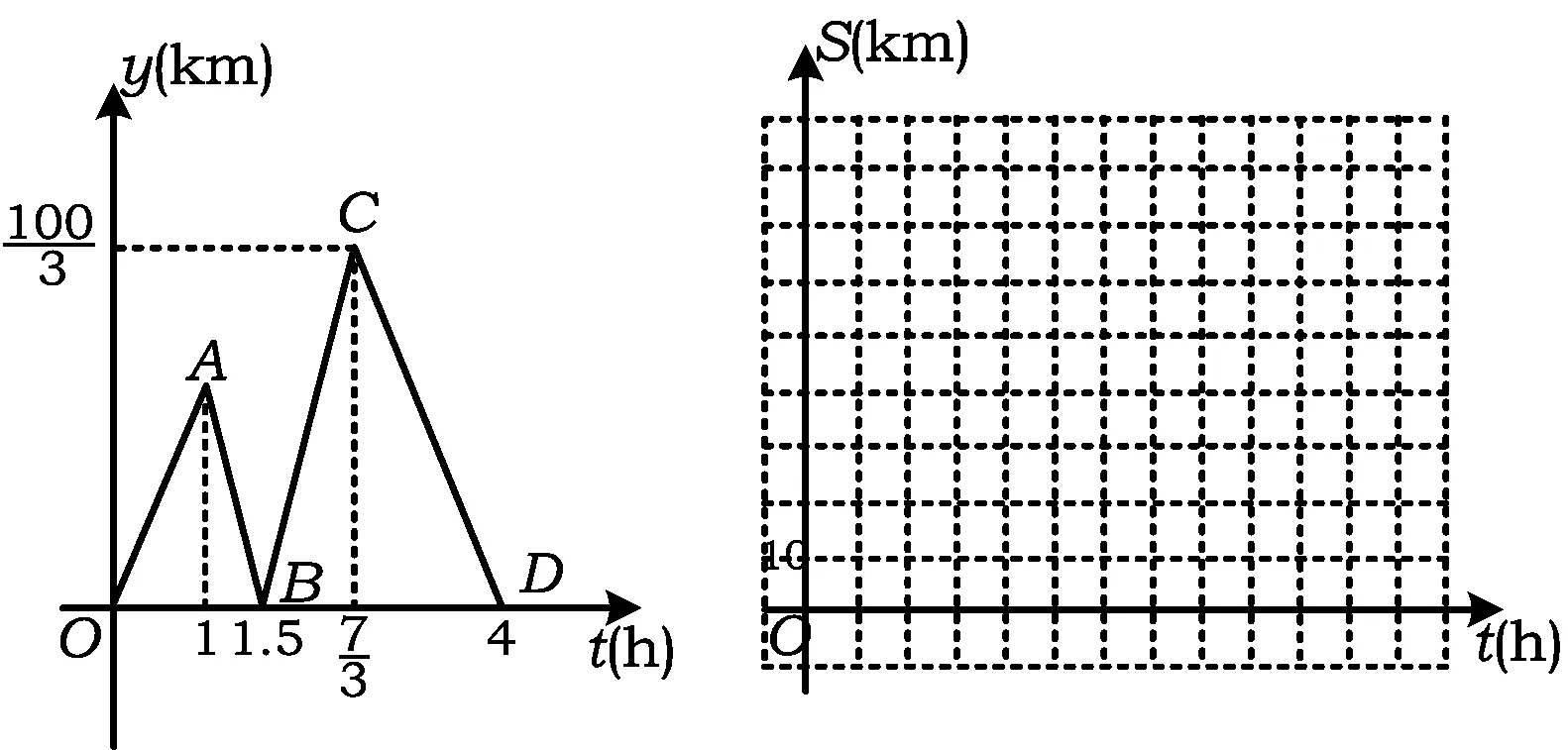
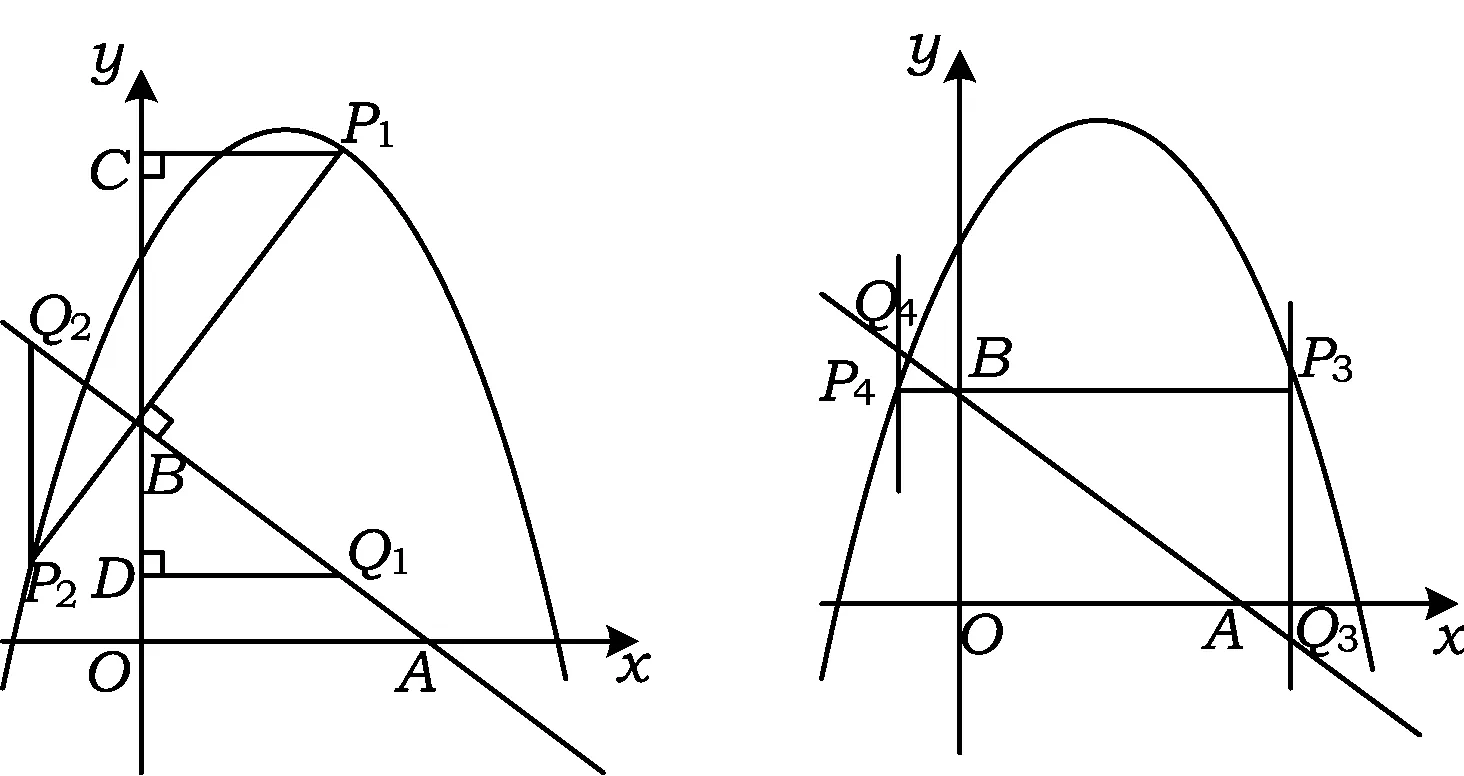
例3方成同学看到一则材料：甲开汽车、乙骑自行车从M地出发沿一条公路匀速前往N地．设乙行驶的时间为t(h)，甲、乙2人之间的距离为{y(km)}，y与t的函数关系如图3所示．

方成思考后发现了如图3的部分正确信息：乙先出发1 h；甲出发0.5 h与乙相遇；……

请你帮助方成同学解决以下问题：

1)分别求出线段BC，CD所在直线的函数表达式；

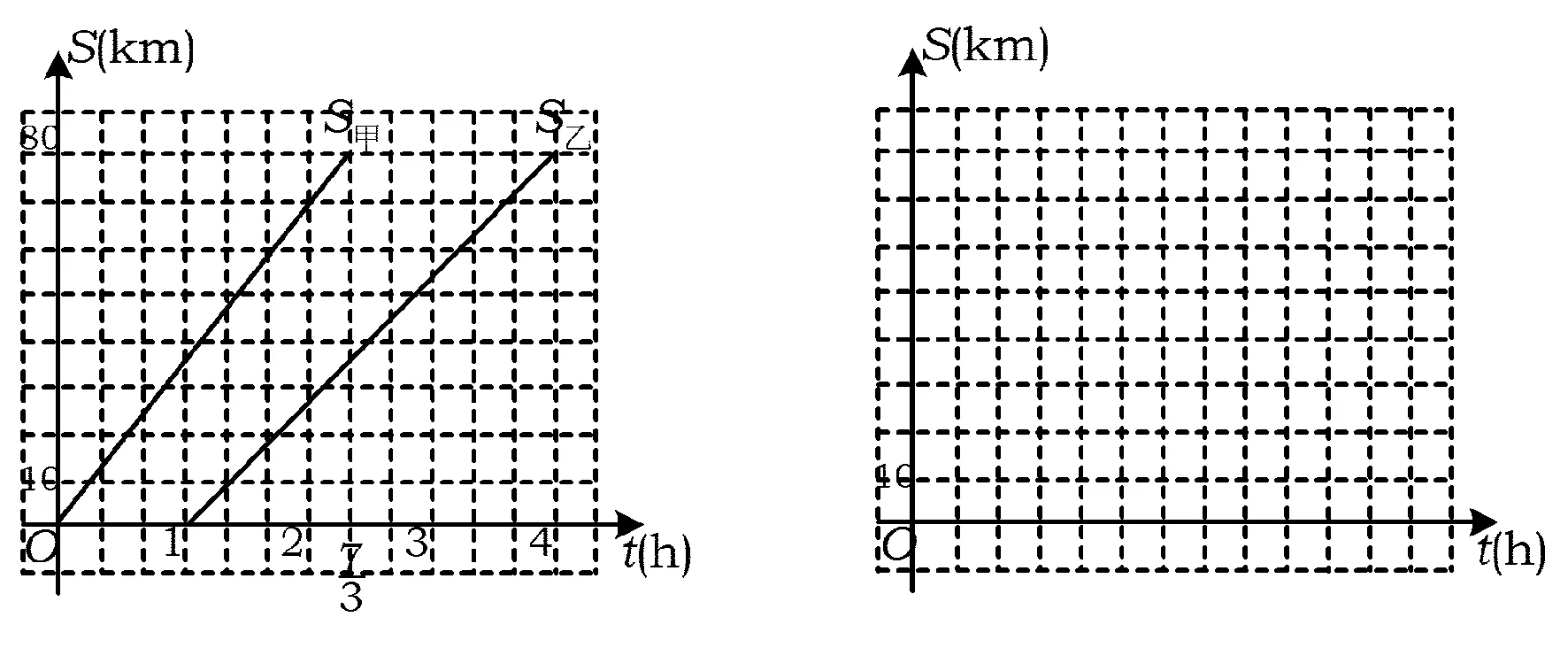
2)当20

3)分别求出甲、乙行驶的路程S甲，S乙与时间t的函数表达式，并在图4所给的直角坐标系中分别画出它们的图像；

图3 图4

(2015年浙江省杭州市数学中考试题)

改编方成同学看到一则材料：甲开汽车、乙骑自行车从M地出发沿一条公路匀速前往N地．设乙行驶的时间为t(h)，甲、乙2人离M地的距离分别为S甲，S乙(km)，且S甲，S乙关于t的函数图像如图5所示．

图5 图6

请你帮助方成同学解决以下问题：

1)分别求出S甲，S乙关于t的函数表达式；

2)设甲、乙2人之间的距离为y,当20

3)在图6所给的直角坐标系中画出y关于t的图像；

(2015年浙江省宁波市数学中考试题)

图7 图8

上述这2类试题的改编方法很常见:一个是将条件与结论互换，另一个是对条件进行类似的改变，目的就是培养学生善于总结出相同类型问题的能力.通过形异质同、多题归一试题改编的教学，挖掘习题深层次的知识点，让学生不仅会解一道题而且会解一类题,从而帮助学生迅速找到解题的策略和方法，培养学生数学思维的深刻性.

3试题改编与数学思维批判性的培养

(2015年浙江省义乌市数学中考试题)

图9 图10

图11

例6如图11，某农场拟建2间矩形饲养室，一面靠现有墙(墙足够长)，中间用一道墙隔开，并在如图11所示的3处地方各留1 m宽的门．已知计划中的材料可建墙体(不包括门)总长为27 m，则能建成的饲养室面积最大为______m2(答案：75)．

(2015年浙江省温州市数学中考试题)

改编某农场拟建2间矩形饲养室，一面靠现有墙，墙长为12 m，中间用一道墙隔开，并在如图11所示的3处地方各留1 m宽的门．已知计划中的材料可建墙体(不包括门)总长为27 m，则能建成的饲养室面积最大为______m2(答案：72)．

改编意图原题改编之后唯一的区别就在于“墙的长度”这一条件，很多学生在做改编题时得到的答案会跟原题一样，而且不知道自己错在哪里.在二次函数求最值问题中，学生比较容易忽视最值能否取到，也就是说学生容易忽视自变量的取值范围.原题设饲养室的宽为x，面积为y,则y={-3(x-5)2}+75(其中1

对于上述2个改编题，目的就是让学生出错，然后让学生自己来纠错，渐渐地弄明白为什么会错，原来是受思维定势的影响.“错在哪里，仔细对比，2道题一样吗？”只有让学生自己去发现，以后犯错的可能性才会降低.让学生明白要正确的看待2道看上去类似的题目，要善于发现问题，提出疑问，辨别是非，提高数学思维的批判性.

4试题改编与数学思维灵活性的培养

(2015年浙江省衢州市数学中考试题)

图12 图13

图14 图15

改编意图抛物线与等腰三角形或直角三角形相结合的问题很常见，这2类问题经常用到分类讨论和一题多解的数学思想.尤其是一题多解的思想，在同一问题不同的情况下，为了更方便地解决问题，用到的方法可以不一样，需要学生灵活地处理.例如改编题中的直角三角形问题，首先根据直角三角形的特征和条件，分为2种情况：①如图14，当∠PBQ=90°时，表示出点P，Q的坐标后可以根据勾股定理求出a的值.也可以构造“直M”型相似，即△PCB∽△BDQ，再根据“相似三角形的对应边成比例”求出a的值；还可以根据“直角三角形斜边上的中线等于斜边的一半”去求(当然笔者最喜欢的还是利用直线PB⊥AB，依据2条直线垂直，2条直线的斜率值乘积等于-1，求出直线PB的解析式，再将直线PB的解析式和抛物线的解析式联立方程组，解方程组即可求出P1和P2这2种情况).②如图15，当∠BPQ=90°时，前面的方法都可以求，但是此时点P的纵坐标与点B的纵坐标相等，直接将y=3代入二次函数解析式即可求出P3,P4这2种情况.因此本题改编的目的就是培养学生选择方法的灵活性和思维的灵活性.

例8已知抛物线y=(x-m)2-(x-m)，其中m是常数．

1)求证：不论m为何值，该抛物线与x轴一定有2个公共点.

①求该抛物线的函数解析式；

②把该抛物线沿y轴向上平移多少个单位长度后，得到的抛物线与x轴只有1个公共点？

(2015年浙江省宁波市数学中考试题)

改编已知抛物线y=(x-m)2-(x-m)，其中m是常数．

1)求证：不论m为何值，该抛物线与x轴一定有2个公共点；

2)当m≠0且m≠-1时，把该抛物线进行左右或上下的平移，使得平移之后的抛物线与坐标轴有2个交点，试讨论m的取值，并求出最短的平移距离．

教师要引导学生在解题遇到困难时及时调整思维的方向，修定原订方案，不受思维定势和固定模式的束缚，能冷静地面对问题，同时又能灵活地处理.或者在已有的思想方法上再另辟蹊径，善于发现新的条件和新的因素，找到众多解法，再从这些解法中提炼出最优方法.这样学生才会越学越轻松，思维也会越来越灵活.

总之，灵活、合理地改编原有的数学试题能提高学生的解题能力，提升数学思维的品质，在解题教学过程中，起着不可估量的作用.数学思维的广阔性、深刻性、批判性和灵活性并不是孤立的，它们相辅相成，相互促进.它们常能使问题由大化小、由小化了，巧妙而简捷地得到解决，让人顿觉思路自然，条理清晰，显示出数学特有的不容辩驳的逻辑力量和数学美感.