改革中凸显平稳 过渡中张扬新意——对2015年广东理科压轴题的评析

改革中凸显平稳过渡中张扬新意——对2015年广东理科压轴题的评析

●蓝云波(兴宁市第一中学广东兴宁514500)●吕孙忠(北京师范大学研究生院北京100875)

备受瞩目的2015年高考终于落下了帷幕，迷雾已拨开.由于2015年是广东省高考自主命题的最后一年，试题的质量与难度受到各界的广泛关注.笔者试做全卷试题，欣喜地发现命题者在平稳过渡的基础上还实现了创新.特别是作为重头戏的压轴题，打破了近几年以函数与导数为主的单一局面，体现出命题者锐意创新的魄力与勇气，给僵化的命题风格带来了一缕清风.本文针对2015年广东省数学高考理科卷的压轴题，谈谈该题的评价、解法、题源与背景揭示以及由此引发的教学反思与建议.

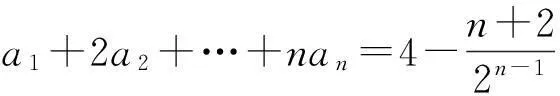
1)求a3的值；

2)求数列{an}的前n项和Tn；

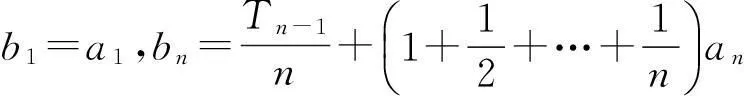
1试题评价

本题具有3个特点：

1)这是一道涉及数列、函数与导数、不等式的综合解答题，这些都是高中数学课程中的主干与核心知识，很好地体现了“高考重点知识重点考查”的原则，及“在知识交汇处命题”的思路.同时考查了数学的重要思想方法，如等价与转化思想、函数思想、分类讨论思想.该题是一道融知识与思想方法于一体的好题.

2)本题面目温和、表述简洁、设问层层递进，易于入手而深入较难，是一道能较好甄别出各个思维层次学生的知识与能力水平的试题，体现出高考试题应具有的选拔功能.

3)本题较好地与教材接了地气，证明过程中要构造的函数正是源于教材的一道练习，体现出“高考源于课本而高于课本”的原则.另外，本题具有深刻的高等数学背景，如阿贝尔变换、积分不等式等，体现出命题者高屋建瓴的高超命题技艺，使试题具有一定的深度与新意.

2解法探究

2.1第1)小题的解答

分析第1)小题的起步比较低，因此解题者起步的心情也是比较愉悦的.最简单的方法就是通过构造2个式子相减得a3.

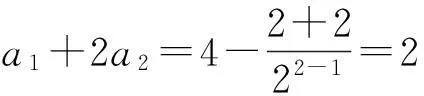
2.2第2)小题的解答

分析第1)小题为第2)小题的解答作了一个从特殊到一般的铺垫，如果解题者通过构造2个式子相减得到a3，那么过渡会相当自然.另外,这一小题看似是用数学归纳法可以解决，实际却不然.

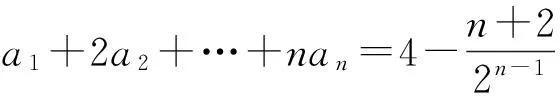
(1)

所以当n≥2时，

式(1)-式(2)，得

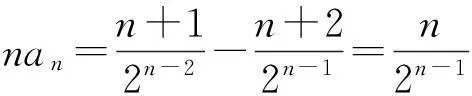
从而

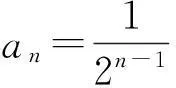
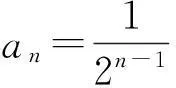
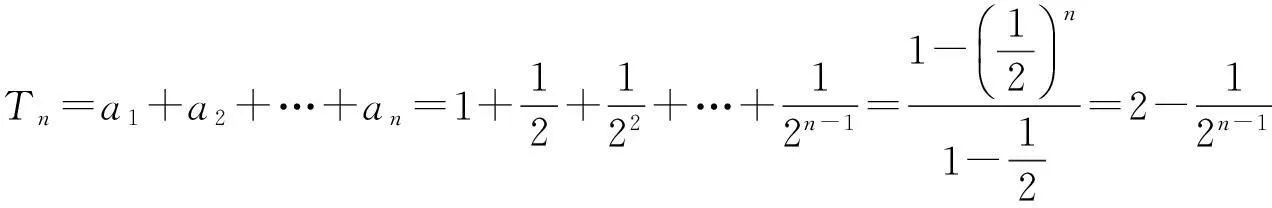
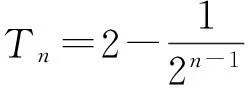
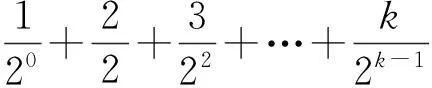
2.3第3)小题的解答

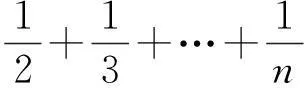
2.3.1第1类方法

Sn=b1+b2+…+bn=

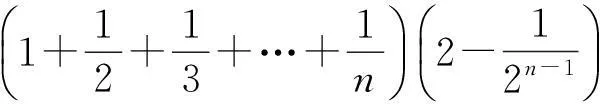
Sn=b1+b2+…+bn=

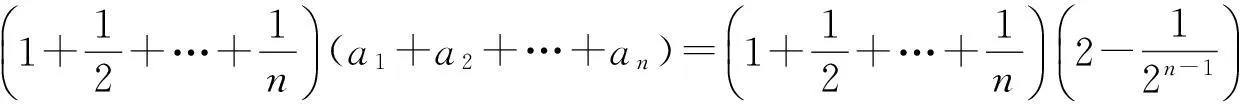
证法3(裂项相消)当n≥2时，

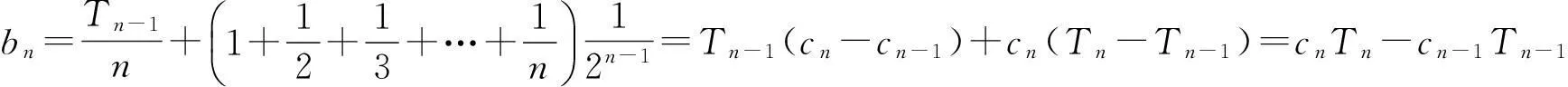
因此当n≥2时，

Sn=b1+b2+…+bn=1+(c2T2-c1T1)+(c3T3-c2T2)+…+(cnTn-cn-1Tn-1)=1+cnTn-c1T1=

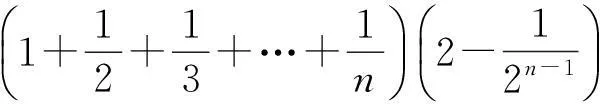
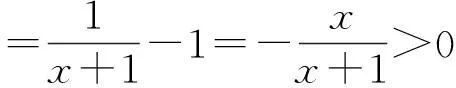
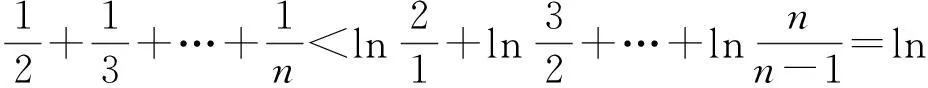
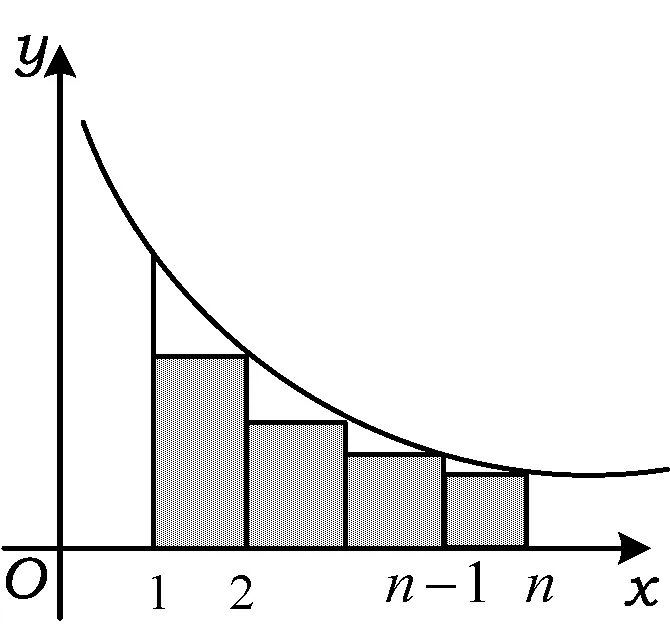
图1

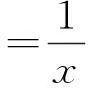
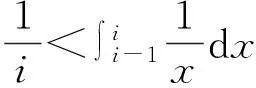
从而

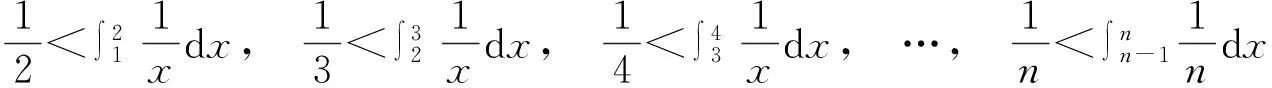
连加可得

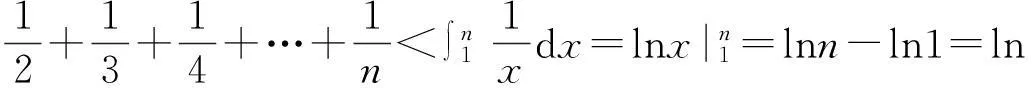
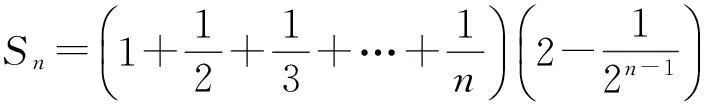
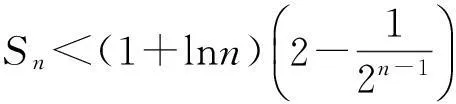
2.3.2第2类方法

分析当n≥3时，

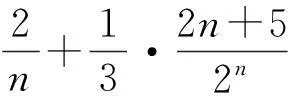
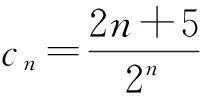
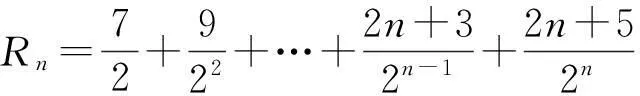
进而

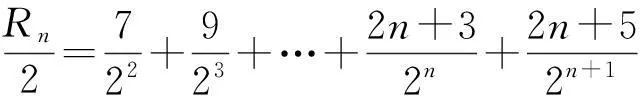
2个式子相减,得

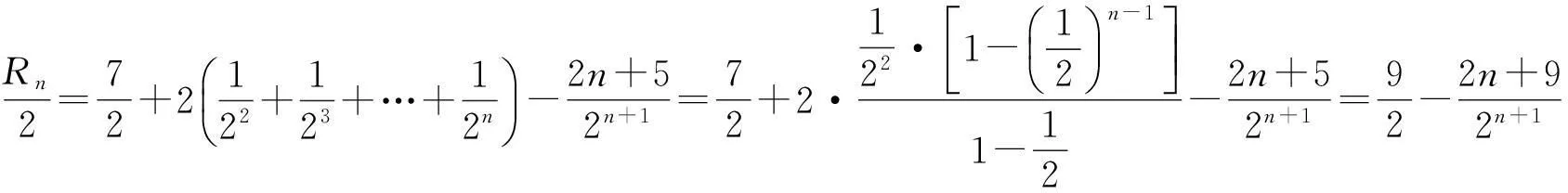
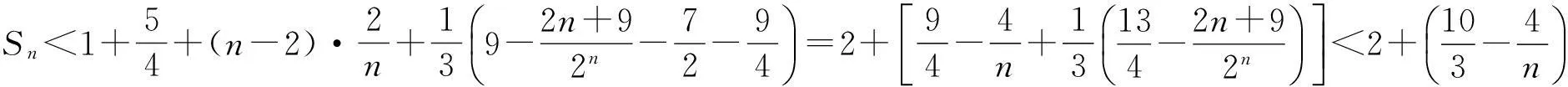
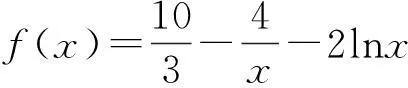
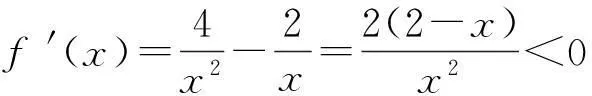
因此f(x)在[3,+∞)上单调递减，即

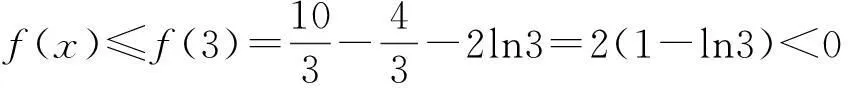
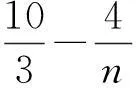
综上可知，对任意正整数n，恒有Sn<2+2lnn.

证明第3)小题的第1类方法分为2步，每一步分别用了4种和2种方法，如果组合一下，就可以得到8种不同的方法.从解题步骤中可以领会到：第3)小题的条件与结论之间的关系较为隐秘，表面上的复杂会让问题变得模糊不清，而通过因式分解和近似替换，可以让问题柳暗花明，化繁为简.第2类方法纯粹是不等式的放缩，放缩完之后再构造一个函数证明不等关系，但这种解法更具一般性，并且这种“放缩-构造”法是“秒杀”众多高考压轴题的利器.

3题源与背景揭示

一题一世界，一解一源泉.解题的根本在于寻根探源，这样才可以深化对解题过程的理解.

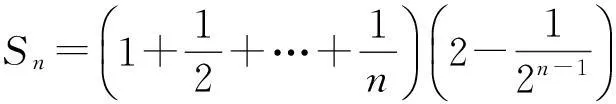
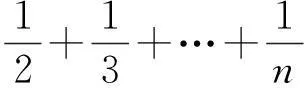
4教学反思与建议

本题是一道综合了数列、函数与不等式的难题.要想成功解答，需具备扎实的基本功及解题能力.因此，教师在教学的过程中，应做到以下3点：

1)重视教材，重视学生的基本功训练.本题虽然是一道压轴题，但其中体现出的数学思想与方法却并非高不可攀.教材中有大量值得教师与学生一起探究与学习的材料，教师应充分利用这些资源，激发学生学习的兴趣，使学生在探究中提高基本技能.如本题第3)小题需要构造的函数正是源于课本的一道经典习题.教师要在平时的教学中重视教材、引领学生进行探究，做到触类旁通、心中有数.

2)重视学生数学思想的培养.在教学中要重视学生的数学思想方法的发生、生成、内化、升华过程.这是数学基本功中的“内力”，并非一朝一夕能改变，教师要意识到这是细水长流的过程，不能急功近利，而是要让学生在长期的接触与体会中得到升华.

3)教师应善于学习，努力提高自己的业务能力，要能站在较高的角度看待和审视问题.这样才能识别出隐藏在试题背后的核心数学思想，并挖掘其中有价值的东西传授给学生，做到“会当凌绝顶，一览众山小”.