2道函数零点高考题的比较与思考

2道函数零点高考题的比较与思考

●张立建(建湖高级中学江苏建湖224700)

1试题再现

例1设函数f(x)=lnx-ax，g(x)=ex-ax,其中a为实数.

1)若f(x)在(1,+∞)上是单调减函数，且{g(x)}在(1,+∞)上有最小值，求a的取值范围；

2)若g(x)在(-1,+∞)上是单调增函数，试求f(x)的零点个数，并证明你的结论.

(2013年江苏省数学高考试题第20题)

例2已知函数f(x)=x3+ax2+b(其中b∈R).

1)试讨论f(x)的单调性；

(2015年江苏省数学高考试题第9题)

2分析比较

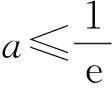
例2第1)小题考查含参数的函数单调区间的讨论，第2)小题因为零点个数已知，从而极值个数和图像形态已知，故只需确定哪个是极大值，哪个是极小值以及需要极大值大于0，极小值小于0即可.

2道题的相同点：都需要讨论含参数的函数的单调区间.不同点：2道题可以看作是逆向问题.例1是在参数a的不同条件下，作函数图像确定零点个数；例2是已知零点的个数，根据函数图像(得到参数满足的不等式)求参数的范围(但这样的设计作为第19题选拔性的试题过于简单，故在此基础上，给出一个参数的范围.增加另外的参数，将问题延伸到不等式恒成立的问题).

3试题解答

例1的第2)小题分析g′(x)=ex-a≥0在{(-1,}+∞)上恒成立，则a≤(ex)min，故

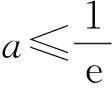
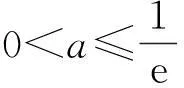
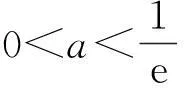
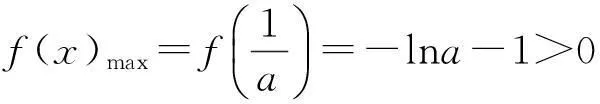
且f(e-1)=-1-ae-1<0,据零点存在性定理知{f(x)}在(e-1,a-1)上有1个零点；又当x∈(a-1,{+∞)}时,需证

f(ea-1)=a-1-aea-1=a(a-2-ea-1)<0,

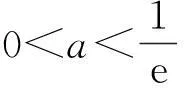
②若a=0，则f(x)=lnx，易得f(x)有1个零点.

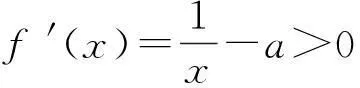
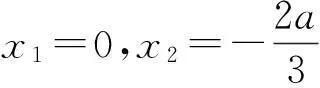
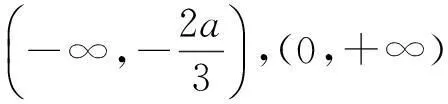
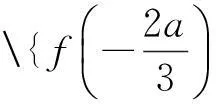
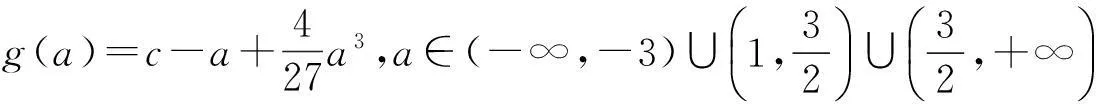
f(x)=x3+ax2+1-a=

(x+1)[x2+(a-1)x+1-a],

由题意知方程x2+(a-1)x+1-a=0有2个异于{-1}的不等实根，即

Δ=(a-1)2-4(1-a)=a2+2a-3>0,

且

(-1)2-(a-1)+1-a≠0，

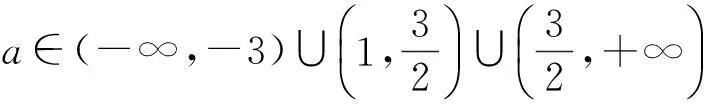
4求真

例1用通法解题思路清晰明了，学生一般都能想到，但对分类讨论能力要求高，易出错.在使用零点存在定理找函数值时，需要一定的知识、方法储备,还要有灵活广阔的思维力.难点是零点存在性定理，难度太大，大部分学生不能完成.

5思考

看过高考试题，感觉高三一年复习下来，费力不讨巧.2015年江苏省数学高考试题重点强调了基础知识和创新应用.知识与能力并重，简单题更加偏重基础知识的理解，中档题更加重视相关知识的运用，难题不再是单纯利用繁琐的计算和复杂的推导过程来增加难度，而是逐渐转变为对方法的思考和灵活运用.

几点启发：1)数学正在回归本源.更加重视知识是什么、为什么、怎么用.数学教学要放低起点，重视概念教学、回归理解、应用.对于双基教学，基础知识要回归课本，而不是加大难度和深度.基本技能要更加重视其形成，多进行横向延伸.2)少一些题目堆积，多一些知识点综合、迁移、转化.重视知识间的联系，加强其综合应用.不一定是多个知识点的整合，2个知识点也可以，重要的是联系、迁移，是学生的认识与感悟，锻炼学生学习及思考的能力、综合解决问题的能力和思维.难题实际上是综合性强的题目，“会者不难”，考查学生对于方法的认识和理解，是对学生思维的考查.3)注重数学的应用.特别是与实际问题的联系，数学来源于生活，又服务于生活.这是数学的初衷和“来龙去脉”.