盘式力矩电机齿槽转矩分析研究❋
2015-12-31杨庆东
王 钦,杨庆东
(北京信息科技大学 机电工程学院,北京 100192)
0 引言
齿槽转矩是产生转矩波动的主要因素之一,数控磨床转台对电机转矩波动有较高要求,因此削弱电机的齿槽转矩对提高磨床转台的回转精度具有重要意义。国内外学者为削弱齿槽转矩总结了许多方法[1-4],本文基于能量法和傅里叶级数解析法提出了一种盘式力矩电机齿槽转矩波动的计算方法,并利用有限元分析工具Ansoft Maxwell建立盘式电机模型和外转子电机模型,通过对比分析验证盘式力矩电机齿槽转矩波动峰值较小的优势。
1 齿槽转矩计算表达式
1.1 齿槽转矩产生机理
盘式力矩电机主要磁场结构如图1所示,它由定子和转子构成。定子由冲卷机一边冲孔一边沿Z轴卷制而成,由于现有绕线技术的限制,定子必须要有齿槽,方便导线嵌入;转子由永磁体和磁轭组成,每一块磁铁均为扇形,N极、S极交替排列。盘式力矩电机磁场方向如图2所示,沿Z轴方向,即电机轴向方向。根据相互作用力原理,转子和定子所受齿槽力大小相等、方向相反,因此分析定子铁芯的受力情况即可得到电机的转子受力情况,进而得到电机的齿槽转矩。
转子旋转过程中,永磁体与定子齿槽产生非线性吸引,力F均匀分布在齿上,转轴垂直于X-Y平面,单齿输出齿槽转矩T是由受力大小相同、半径不同的扭矩叠加形成,电机的齿槽转矩是由所有齿的齿槽转矩叠加而成。齿槽转矩波动峰值在高速运转时表现为振动,当磨床转台小切削量精加工外圆面,齿槽转矩波动峰值产生的振动与磨削颤振共振时,就会在磨削表面产生明显波纹。
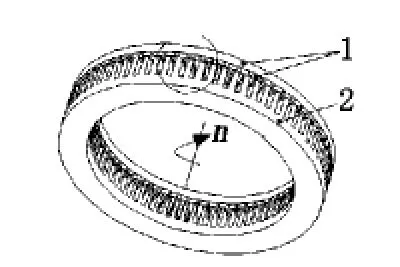
图1 盘式力矩电机磁场结构
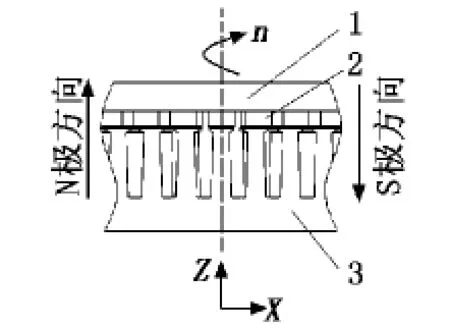
图2 盘式力矩电机磁场方向
1.2 盘式力矩电机齿槽转矩表达式
根据能量法[5],齿槽转矩是由转子旋转时电机能量的变化引起的。忽略永磁体和铁芯的能量变化,假定盘式力矩电机永磁体磁感线穿过的面为矩形,建立的齿槽转矩表达式为:
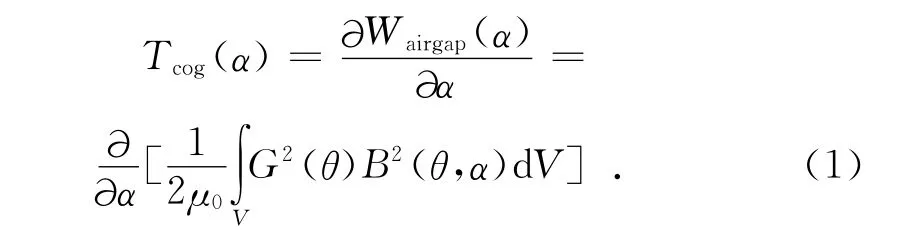
其中:α为转子位置,即永磁体中心线与齿中心线夹角;Wairgap为气隙磁场能量;μ0为空气磁导率;θ为转子角度;G(θ)为气隙相对磁导率;B(θ,α)为无槽时气隙磁密分布;V为求解区域。
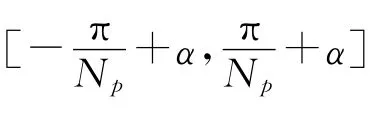

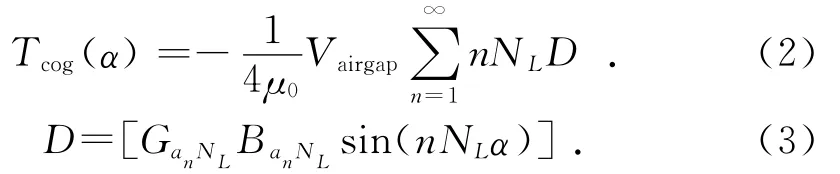
其中:Vairgap为气隙体积;BanNL和GanNL均为傅里叶系数;n为一个整数;NL为Ns和Np的最小公倍数。
气隙体积由下式计算:

其中:R1为定子内半径;R2为定子外半径;g为气隙。

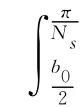
根据磁路定律,计算式(5)中的气隙磁密Bδ的公式为:

其中:Br为剩磁密度;kml为考虑永磁体间漏磁后的系数。计算kml的方程为:

其中:Pg为一个极下气隙磁导;Pm为永磁体磁导;Pml为永磁体间的漏磁。上述几个量的计算方程为:
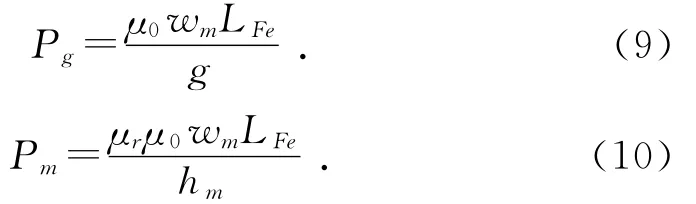

其中:wm为永磁体宽度;LFe为永磁体长度;wf为永磁体间的宽度。
将式(9)~(11)代入式(8)得到kml,将式(8)代入式(7)得到Bδ,将式(7)代入式(5)得到BanNL,将式(4)~式(6)代入式(2)得到径向磁场盘式力矩电机齿槽转矩Tcog(α)的表达式:

从以上分析可以看出,气隙体积Vairgap、气隙磁密Bδ是影响齿槽转矩波动幅值的重要因素;极数和槽数的最小公倍数NL、极弧系数αp是影响齿槽转矩波动频率的重要因素。在设计电机时应尽量减小气隙g以降低齿槽转矩波动最大值;在选取极槽配合参数时,应考虑电机工况,避开共振频率。气隙磁密Bδ是永磁体能量的表现形式,气隙磁密越大,电机磁能越大,输出扭矩的能力越大,通过优化极弧系数在保证气隙磁密正弦分布的同时也可改善齿槽转矩波动。
由于本文采用的能量法解析计算模型将平底槽型简化成矩形,假定气隙磁密为矩形,磁通集中存在于齿部,实际上槽口处也存在磁通,使得计算结果偏小。
2 计算与仿真
为证明盘式力矩电机齿槽转矩较小的优势,本文以外转子力矩电机作为对比对象进行分析。电机主要参数如表1所示。
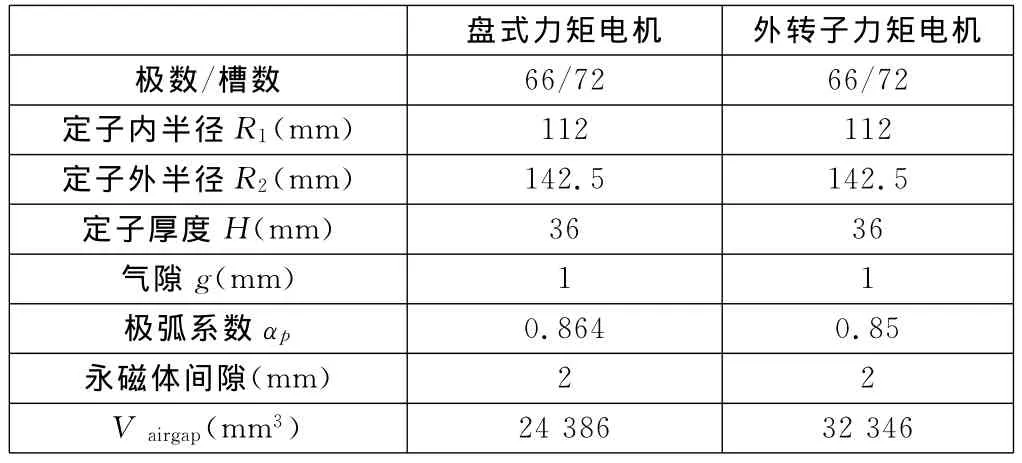
表1 电机主要参数表
将两个电机参数代入式(12),计算结果如图3所示。因盘式力矩电机的气隙体积Vairgap较小,所以齿槽转矩波动峰值较小。
使用有限元工具Ansofe Maxwell建立电机仿真模型。根据电磁场的对称分布原理,计算一个对称单元即可,即1/6个电机。因磁场方向为轴向,2D切面无法完整反映电磁分布,所以盘式力矩电机要用3D仿真模型进行计算,但外转子电机使用2D仿真模型即可。有限元模型参数设定如表2所示。

图3 齿槽转矩表达式计算对比

表2 有限元模型参数设定表
通过多次仿真发现,将外转子电机2D模型Max Length(最大长度)设定为0.5mm,Normal Deviation(正态偏差)设定为0.2°是最佳值,此时增大网格数量仿真波形变化不明显,已经达到了有限元计算的最佳精度。
3D运算量比2D大很多,为达到3D最佳运算精度,需找到电脑性能所能承受的最大值,经过多次尝试发现,盘式力矩电机Max Length(最大长度)设定为2mm,Normal Deviation(正态偏差)设定为5°~10°是极限值,如果再增大网格数量,电脑就会内存不足无法运算,如果减小网格数量,波形趋势基本不变,能够满足运算精度。齿槽转矩有限元计算结果如图4所示。
理论计算与有限元仿真结果对比如表3所示。从表3中可以看出,两种计算方法得出的结果都显示盘式力矩电机齿槽转矩较小,理论计算结果显示盘式力矩电机齿槽转矩比外转子力矩电机减小24.5%。有限元计算结果较为精确,结果显示盘式力矩电机齿槽转矩比外转子力矩电机减小28.9%,η1与η2相差4.4%,由此证明式(12)能够在一定程度上反映齿槽转矩波动的规律,但是由于模型简化较多,幅值误差较大。

图4 齿槽转矩有限元计算结果
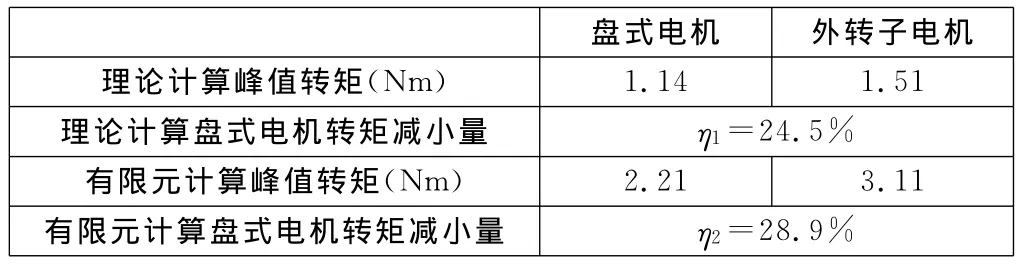
表3 理论计算与仿真结果对比表
3 结论
本文推导了盘式力矩电机齿槽转矩波动表达式,建立有限元模型对盘式力矩电机和外转子力矩电机的齿槽转矩波动进行了对比仿真计算。仿真结果表明,在槽型结构、永磁体间隙、定子冲片外形尺寸相同的条件下,盘式力矩电机齿槽转矩波动幅值减小25%,气隙体积Vairgap是影响齿槽转矩波动峰值的重要因素。为提高转台加工精度,减小齿槽转矩波动,可将盘式力矩电机嵌入转台内,设计电机时应尽量减小气隙,以减小转矩波动峰值。
[1]刘婷.表贴式永磁同步电机齿槽转矩削弱方法研究[D].长沙:湖南大学,2013:7-12.
[2]邓秋玲,黄守道,刘婷,等.永磁电机齿槽转矩的研究分析[J].湖南大学学报(自然科学版),2011(3):56-59.
[3]杨玉波,王秀和,朱常青.基于分块永磁磁极的永磁电机齿槽转矩削弱方法[J].电工技术学报,2012(3):73-78.
[4]黄守道,刘婷,欧阳红林,等.基于槽口偏移的永磁电机齿槽转矩削弱方法[J].电工技术学报,2013(3):99-106.
[5]朱莉,姜淑忠,诸自强,等.表面式永磁电机齿槽转矩解析模型比较[J].微电机,2010(1):10-15.
