发动机支架疲劳寿命分析——基于威布尔分布法

文/黄安心 张叶亮

发动机支架在经过设计、铸造、热处理、加工和喷涂工序后，都要通过台架疲劳试验来检验设计和开发的有效性，使用寿命期中的可靠性分析是必不可少的步骤。它可以分析失效产生的机理，为改进和优化设计提供参考。

可靠性分析是通过数量有限的台架试验样本来评价整批产品的可靠性、失效机理线索等。可靠性分析有很多种方法可用于统计分析和评价，常用的寿命分析分布形式有威布尔分布、正态分布、指数分布和对数正态分布等。其中，威布尔分布是除正态分布以外常用于可靠性分析的一种分布形式。机械零件失效具有明显的耗损特征，威布尔分布通常被用于它们的寿命和可靠性分析。汽车发动机支架随汽车在行驶过程中承受随路面的随机载荷，峰值应力远小于其屈服强度，其失效主要为疲劳断裂。而发动机支架作为承载动力源的重要零件，必须确保其寿命大于汽车的安全寿命里程。因此，我们不但关心其在一定可靠度下的寿命，更关心其最小寿命，而基于三参数威布尔分布的可靠性分析恰恰能得到我们想要的结果。所以，三参数威布尔分布在汽车零件的可靠性分析中有很高的现实意义和实用价值。

一、三参数威布尔分布介绍

威布尔分布是瑞典科学家威布尔（W. Weibull）1951年在研究材料强度时，提出的一种概率分布函数。它具有适用性广、覆盖性强、在威布尔概率纸上表示直观、能以较少的试验样本得出较准确的失效分析、能包容其他多种分布形式等特点。国内外，威布尔分布已在强度、环境研究领域及以损耗为特征的机械零件寿命评估中得到广泛的应用。它有多种形式，包括单参数、二参数、三参数及混合威布尔。与其他威布尔分布相比，将三参数威布尔分布运用于汽车发动机支架具有多个优点：

・在威布尔概率纸上拟合精度更高，即一定可靠度下的寿命结果更准确；

・能得出最小寿命，对维修保养甚至汽修厂备件储备能提供重要依据。

由于威布尔分布参数的分析估计法较复杂，区间估计值过长，故以前常采用概率纸估计法，参数的估计精度较低。现在，随着计算机软件的发展，能快速方便地输出威布尔概率纸及其拟合直线，并输出计算结果。

二、三参数威布尔分布理论

三参数威布尔分布函数为：

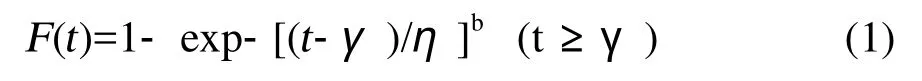
式中：b为形状参数，b>0；

η为尺度参数，η>0；

γ为位置参数，也称最小寿命，表示产品在γ以前不会失效。对于产品寿命有γ≥0，γ=0时退化为二参数威布尔分布；

t为产品工作时间，t≥γ。

对公式（1）两边取2次自然对数得：

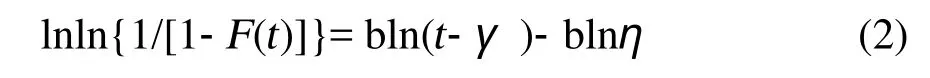
设X= ln(t-γ)，Y= lnln [1-F(t)]-1，A=blnη，则公式(2)变成Y= bX-A。在t-F(t)坐标系下的一条威布尔分布函数在X-Y坐标系下对应为一条斜率大于0的直线。斜率b是一个非常重要的参数，它可以提供一些失效的机理或线索：

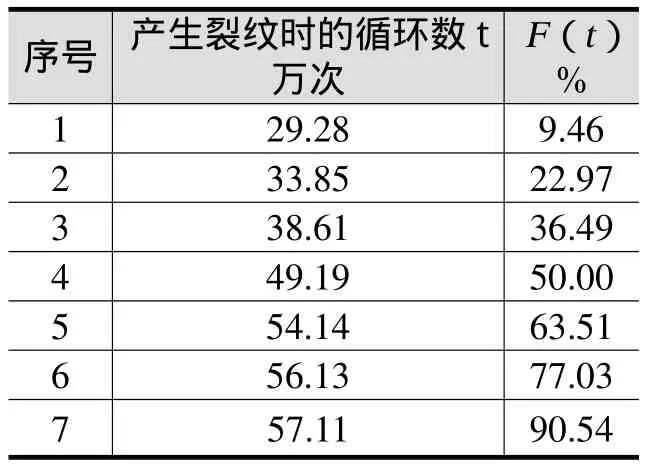
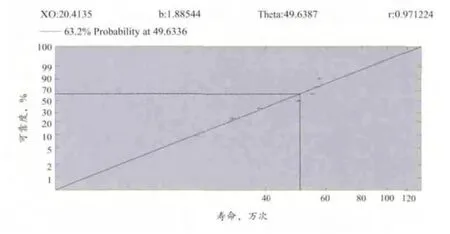
若0

若b=1，说明是随机失效，可能是人为原因，外来偶发因素造成；

若b>1，说明为损耗失效，可能是材料固有属性限制，较大的斜率说明失效前都有一个稳定的安全期，产品质量具有较高的一致性。

对于分布参数的估计有点估计法和区间估计法，其中，点估计法有很多种，如最小二乘法、平均法、线性估计法、极大似然估计法和相关系数优化法等；区间估计法有Monte-Carlo模拟法、回归法等。本文主要采用求相关系数最大时对应的位置参数，把三参数简化为两个参数，在γ已知时利用最小二乘法或极大似然估计进行回归求出b和A， 进而求出尺度参数η= e 。此法不仅最大限度地得到线性关系，而且得到的相关系数还可用于分布检验。

x和y之间的相关系数R(x, y)为：

R(x, y)是衡量x和y两变量之间的线性关系程度，相关系数总是在-1和+1之间，越接近于1，相关性越好。R(x, y)是位置参数γ的函数，γ应是使R(x, y)最大位置参数，即dR(x,y)/dγ=0。

可靠性一般以两种方式来表示：一种是以可靠度来表示，F(ti)为累计失效概率，可靠度用R(ti)=1-F(ti)，表示为第i个产品失效时的累计失效概率，可用中位秩算法或平均秩算法求得，在寿命数据中非均匀分布相当常见。所以，中位秩算法比平均秩算法更为准确些；另一种以（B+寿命）表示，如B0.1表示工作到寿命N时有0.1%的零件失效。

三、发动机支架疲劳寿命分析

本文针对某型发动机支座的疲劳试验结果，对其进行威布尔分布分析。

该发动机支座为铸造铝合金结构（见图1）。其底座有3个螺栓孔A、B和C，用于固定其位置。座体材料为AS7，其弹性模量为74 000 MPa，泊松比为0.33，密度为2.7×103 kg/m3，屈服强度为190 MPa。试验样品为从试制的批次中随机抽取7件，载荷为正弦波形，大小为±8 000 N，按图2所示方向加载。

图1 发动机支座三维结构

图2 载荷加载位置和方向

按照发动机支架的实车安装状态和加载要求，搭建了试验台架（见图3），依次对发动机支架进行疲劳试验。记录出现裂纹的位置（见图4）和出现裂纹时的加载循环数，试验结果按照循环数由小到大的顺序排序（见表1）：

图3 加载试验台架

图4 裂纹发生位置

表1 发动机支架疲劳试验结果（中位秩法）

图5 威布尔分布拟合直线图

采用nsoft软件中的数据统计分析模块，选择采用行列中值回归法作为威布尔分布参数估计方法，快速地输出威布尔概率纸及其拟合直线，并输出计算结果。本文使用该软件输出，结果见图5。

从图5可以看出，这些点可以比较好地拟合成直线，说明发动机支架的寿命符合威布尔分布，它直观地反映出支架疲劳寿命与累积失效概率的相互关系（见表2）。

表2 可靠度（累积失效概率）和支架疲劳寿命的关系

其中，特征寿命（B63.2）η= 49.633 6万次，形状参数b=1.885 45，位置参数（最小安全寿命）γ= 20.413 5，相关系数 r = 0.971 224。

形状参数b大于1，说明为疲劳失效形式，失效前有一个稳定的安全期，失效率函数是单调增加的，意味着越到寿命后期失效率越高。产品质量具有较高的一致性，提高产品可靠性的途径主要可通过改进设计和更换材料来实现。

四、结 论

根据发动机支架的受载要求，合理搭建疲劳测试台架，得出有限样本情况下的发动机支架疲劳寿命数据，并应用威布尔分布理论，分析疲劳寿命结果，验证其寿命符合威布尔分布。

通过三参数威布尔分布疲劳分析工具，得出威布尔分布的特征参数、疲劳寿命与累积失效概率等关系，根据形状参数，分析查找失效原因。若是早期失效则需从设计、制造、装配等环节入手查找原因；若是损耗失效，则需从改进结构、更换材料、工艺入手来提升产品可靠性。

对于工程中常见的小样本情况，样本所服从分布的参数本身也是随机变量，它服从一定的概率分布，在要求高置信度、高可靠度的条件下，仅仅用由参数点估计值得到的分布来进行推断还不够，通常采用参数区间估计法得出置信限。威布尔分布作为试验数据分析工具用于产品可靠性分析，可以提供更多的产品性能和质量信息，为改进和优化设计提供参考。

[1] 吴波,黎明发.机械零件与系统可靠性模型.北京:化学工业出版社，2003.

[2] 方志强,高连华.三参数威布尔分布在寿命分析中的参数估计[J].装甲兵工程学院学报，1999;13(3):12-15.

[3] 傅惠民,高镇同.确定威布尔分布三参数的相关系数优化法[J].航空学报,1990, 7(11):323-327.

[4] 严晓东,马翔等.三参数威布尔分布参数估计方法比较[J].宁波大学学报,2005,18(3):301-305.