关于数字5与7的神奇特征



关于数字5与7的神奇特征

王仲才

（南昌理工学院江西南昌330044）

摘要：本文给出数字5与7的神奇特征，即接连的5个与7个正整数、偶数、奇数的1次方、2次方、3次方之和分别都是5与7的整数倍。

关键词：5；7；正整数；平方；立方；作和

［引理1］接连的5个正整数之和是5的整数倍

证明设n为正整数，则接连的5个正整数是

n,n+1,n+2,n+3,n+4

它们之和是

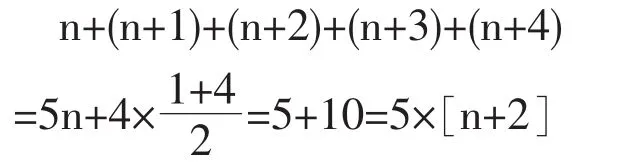
证毕

［引理2］接连的5个偶数之和是5的整数

证明设n为正整数，则接连的5个偶数是

2n,2（n+1）,2（n+2）,2（n+3）,2（n+4）

它们之和是

2×［n+(n+1)+(n+2)+(n+3)+(n+4)］

［引理1］得知，它等于5×［2n+4］

证毕

［引理3］接连的5个奇数之和是5的整数倍

证明设n为正整数，则接连的5个奇数是

2n-1,2n+1,2n+3,2n+5,2n+7

它们之和是

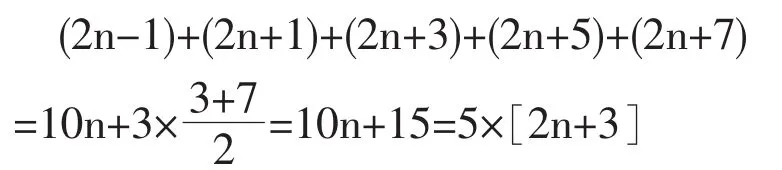
证毕

［定理1］接连的5正整数的平方和是5的整数倍。

证明设n为正整数，则接连的5个正整数的平方和是

n2+(n+1)2+(n+2)2(n+3)2(n+4)2

=n2+(n2+2n+1)+(n2+4n+4)+(n2+6n+9)+(n2+8n+ 16)

=5n2+20n+30=5×［n2+4n+6］

证毕

［推论1］接连的5的正整数倍个正整数的平方和是5的整数倍.

证明：每5个一组，由［定理1］即得结论.

证毕

［定理2］接连的5个偶数的平方和是5的整数倍.

证明：设n为正整数，由［引理2］接连的5个偶数的平方和是

(2n)2+［2(n+1)］2+［2(n+2)］2+［2(n+3)］2+［2(n+4)］2

由［定理1］得知，它等于

5×［4n2+16n+24］

证毕

［推论2］接连的5的整数倍个偶数的平方和是5的整数倍.

证明：每5个一组，由［定理2］即得结论.

证毕

［定理3］接连的5个奇数的平方和是5的整数倍.

证明：设为正整数，则接连的5个奇数的平方和是

(2n-1)2+(2n+1)2+(2n+3)2+(2n+5)2+(2n+7)2

=(4n2-4n+1)+(4n2+4n+1)+(4n2+12n+9)+(4n2+ 20n+25)+(4n2+28n+49)

=20n2+60n+8.5

=5×［4n2+12n+17］

证毕

［推论3］接连的5的正整数倍个奇数的平方和是5的整数倍.

证明：每5个一组，由［定理3］即得结论.

证毕

［定理4］接连的5个正整数的立方和是5的整数倍.

证明：设n为正整数，则接连的5个正整数的立方和是

n3+(n+1)3+(n+2)3(n+3)3(n+4)3

=n3+(n3+3n2+3n+1)+(n3+6n2+12n+8)+(n3+9n2+ 27n+27)+(n3+12n2+48n+64)

=5n3+30n2+90n+100

=5×［n3+6n2+18n+20］

证毕

［推论4］接连的5的正整数倍个正整数的立方和是5的整数倍.

证明：每5个一组，由［定理4］.即得结论.

证毕

［定理5］接连的5个偶数的立方和是5的整数倍.

证明：设n为正整数，接连的5个偶数的立方和是

8［n3+(n+1)3+(n+2)3+(n+3)3+(n+4)3］

由［定理4］得知，它等于

5×［8n3+48n2+144n+160］

证毕

［推论5］接连的5和正整数倍个偶数的立方和是5的整数倍.

证明：每5个一组，由［定理5］即得结论.

证毕

［定理6］接连的5个奇数的立方和是5的整数倍.

证明：设n为正整数，则接连的5个奇数的立方和是

(2n-1)3+(2n+1)3+(2n+3)3+(2n+5)3+(2n+7)3

=(8n3-12n2+6n -1) +(8n3+12n2+6n +1) +(8n3-36n2+54n+27)+(8n3+60n2+150n+125)+(8n3+84n2+ 294n+343)

=40n3+180n2+510n+495

=5×［8n3+36n3+102n2+99］

证毕

［推论6］接连的5的正整数倍个奇数的立方和是5的整数倍.

证明：每5个一组，由［定理6］即得结论.

证毕

［引理4］接连的7个正整数之和是7的整数倍.

证明设n为正整数，则接连的7个正整数是

n,（n+1）,（n+2）,（n+3）,（n+4），（n+5）,（n+6），

它们之和是

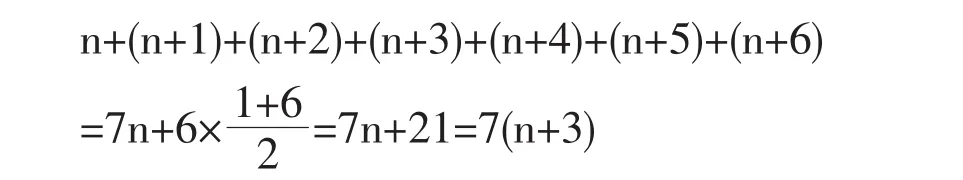
证毕

［引理5］接连的7个偶数之和是7的整数倍.

证明设n为正整数，接连的7个偶数是

2n,2（n+1）,2（n+2）,2（n+3）,2（n+4），2（n+5），2 （n+6），

它们之和是

2n+2（n+1）+2（n+2）+2（n+3）+2（n+4）+2（n+5）+2（n+6）

=2×7(n+3)=7(2n+6)

证毕

［引理6］接连的7个奇数之和是7的整数倍

证明：设n为正整数，接连的7个奇数是

2n-1,2n+1,2n+3,2n+5,2n+7,2n+9,2n+11

它们之和是

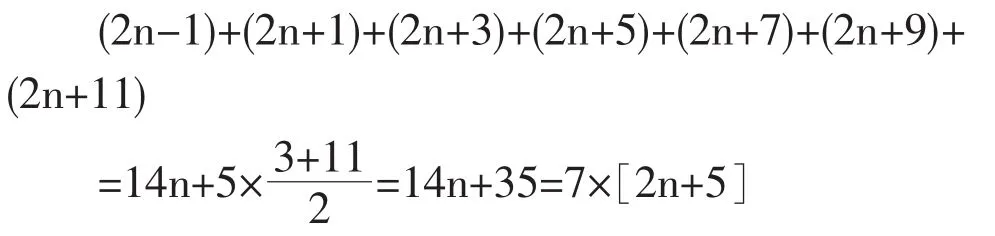
证毕

［定理7］接连的7个正整数的平方和是7的整数倍。

证明设n为正整数，则接连的7个正整数的平方和是

n2+(n+1)2+(n+2)2+(n+3)2+(n+4)2+(n+5)2+(n+6)2

=n2+(n2+2n+1)+(n2+4n+4)+(n2+6n+9)+(n2+8n+ 16)+(n2+10n+25)+(n2+12n+36)

=7n2+42n+91=7×［n2+6n+13］

证毕

［推论7］接连的7的正整数倍个正整数的平方和是7的整数倍.

证明：每7个一组，由［定理7］即得结论.

证毕

［定理8］接连的7个偶数的平方和是7的整数倍.

证明：由［引理5］和［定理7］得知这个和是

4×7×［n2+6n+13］

=7×［4n2+24n+52］

证毕

［推论8］接连的7的整数倍个偶数的平方和是7的整数倍.

证明：每7个一组，由［定理8］即得结论.

证毕

［定理9］接连的7个奇数的平方和是7的整数倍.

证明：由［引理6］得知，7个接连的奇数的平方和是

(2n-1)2+(2n+1)2+(2n+3)2+(2n+5)2+(2n+7)2+(2n+ 9)2+(2n+11)2

=(4n2-4n+1)+(4n2+4n+1)+(4n2+12n+9)+(4n2+ 20n+25)+(4n2+28n+49)+(4n2+36n+81)+(4n2+44n+ 121)

=28n2+140n+287=7×［4n2+20n+41］

证毕

［推论9］接连的7的整数倍个奇数的平方和是7的整数倍.

证明：每7个一组，由［定理9］即得结论.

证毕

［定理10］接连的7个正整数的立方和是7的整数倍.

证明：设n为正整数，则接连的7个正整数的立方和是

n3+(n+1)3+(n+2)3+(n+3)3+(n+4)3+(n+5)3+(n+6)3

=n3+(n3+3n2+3n+1)+(n3+6n2+12n+8)+(n3+9n2+ 27n+27)+(n3+12n2+48n+64)+(n3+15n2+75n+125)+ (n3+18n2+108n+216)

=7n3+63n2+273n+441

=7×［n3+9n2+39n+63］

证毕

［推论10］接连的7的正整数倍个正整数的立方和是7的整数倍.

证明：每7个一组，由［定理10］即得结论.

证毕

［定理11］接连的7个偶数的平方和是7的整数倍.

证明：设n为正整数，则接连的7个偶数的立方和是

(2n)3+［2(n+1)］3+［2(n+2)］3+［2(n+3)］3+［2(n+4)］3+［2(n+5)］3+［2(n+6)］3

=8［n3+(n+1)3+(n+2)3+(n+3)3+(n+4)3+(n+5)3+(n+ 6)3］

由［定理10］得知，它等于

7×［8n3+72n2+504+312n］

证毕

［定理12］接连的7个奇数的立方和是7的整数倍.

证明：设n为正整数，则接连的7个奇数的立方和是

(2n-1)3+(2n+1)3+(2n+3)3+(2n+5)3+(2n+7)3+(2n+ 9)3+(2n+11)3

=(8n3-12n2+6n -1) +(8n3+12n2+6n +1) +(8n3-36n2+54n+27)+(8n3+60n2+150n+125)+(8n3-84n2+ 294n +343) +(8n3-108n2+486n +729) +(8n3-132n2+ 726n+1331)

=56n3+420n2+1722n+2555

=7×［8n3+60n2+246n+365］

证毕

［推论12］接连的7的正整数倍个奇数的立方和是7的整数倍.

证明：每接连的7个一组，由［定理12］即得结论.

证毕

参考文献：

［1］王仲才.关于12与18的整数倍的另一神奇特征（续十一）［J］.江西广播电视大学学报，2013(1).

［2］王仲才.关于数字10的神奇特征（续十二）［J］.江西广播电视大学学报，2013(2).

责任编辑：罗义

[作者简介]王仲才（1939-），男，辽宁辽阳人，原南昌大学教授，硕士生导师，研究方向：几何与微分拓扑学。

[收稿日期]2015－1－27

中图分类号：O1

文献标识码：A

文章编号：1008-3537（2015）02-0094-03