电力系统低频振荡的类型判别研究与分析

周　专，常喜强，张增强，王　衡，张　锋，贠　剑

(1.国网新疆电力公司经济技术研究院，新疆 乌鲁木齐　830016；

2.国网新疆电力调度控制中心，新疆 乌鲁木齐　830006)

电力系统低频振荡的类型判别研究与分析

周专1，常喜强2，张增强1，王衡2，张锋2，贠剑2

(1.国网新疆电力公司经济技术研究院，新疆 乌鲁木齐830016；

2.国网新疆电力调度控制中心，新疆 乌鲁木齐830006)

摘要：随着区域电网互联、电网规模不断扩大和快速励磁系统的大量应用，电力系统动态稳定性问题也越来越突出，逐渐成为影响电网安全和限制输电功率极限的主要因素。由于动态元件的大量投入，改变了系统动态调节性能，若动态稳定性差将容易引发系统低频振荡。系统低频振荡会导致系统出现频率、电压、功率等电气量不同程度振荡的现象，持续恶化的互相作用最终将导致系统失稳、解列，形成大规模的停电事故。因此电力系统低频振荡问题越来越受到人们的关注，而如何正确、快速判别振荡性质成为难于解决的问题。对负阻尼振荡和强迫振荡的特性进行研究，提出了基于起振阶段暂态响应包络线形状的振荡类型判别判据，以某电网低频振荡为实例加以验证，表明所提出的研究方法能有效判断低频振荡类型。对分析实际运行中低频振荡现象以及有效抑制系统低频振荡具有重要的指导意义。

关键词：低频振荡；负阻尼振荡；强迫振荡；响应特性

0引言

20世纪60年代美国西北电力系统与西南电力系统进行互联时，发生了功率的增幅振荡，最终破坏了大系统的并联运行。日本、欧洲等国也先后发生过低频振荡。在中国，随着电网规模的日益扩大以及快速励磁装置使用的增加，也出现过多次低频振荡事故。电力系统一旦发生低频振荡，将严重威胁电网的安全稳定运行，甚至可能诱发连锁反应，造成------------------------

更严重的后果，故低频振荡问题一直是电力系统安全稳定运行中备受关注的重要问题之一，对低频振荡进行深入研究具有十分重要的意义[1-3]。

系统低频振荡会导致系统出现频率、电压、功率等电气量不同程度振荡的现象，持续恶化的互相作用最终将导致系统失稳、解列，形成大规模的停电事故。随着区域电网互联、电网规模不断扩大和快速励磁系统的大量应用，低频振荡出现的概率不断提高，振荡类型越来越多，且低频振荡扰动源定位越来越复杂，加大了分析低频振荡原因及抑制低频振荡的难度[4]。

因此对负阻尼振荡和强迫振荡的特性进行研究，提出了基于起振阶段暂态响应包络线形状的振荡类型判别判据，以某电网低频振荡为实例加以验证，表明所提出的研究方法能有效判断低频振荡类型。对分析实际运行中低频振荡现象以及有效抑制系统低频振荡具有重要的指导意义。

1低频振荡概述

电力系统中发电机经输电线并列运行时,在扰动下会发生发电机转子间的相对摇摆,并在缺乏阻尼时引起持续振荡,此时,输电线上功率也会发生相应振荡。由于振荡频率很低,一般为0.2～2.5 Hz，故称为低频振荡。而随着联网规模的不断增大,低频振荡频率也随之降低至0.l Hz，甚至更低。

根据系统振荡频率的不同范围,将低频振荡分为本地振荡模式和区间振荡模式两种类型。区域内振荡模式:涉及一个发电厂内的发电机组与电力系统其他部分之间的摇摆,其振荡频率一般为1～2 Hz。区域间振荡模式:系统中某一个区域内的多台发电机与另一区域内的多台发电机之间的相对摇摆。当系统表现为两群发电机之间振荡时,振荡频率大致在0.1～0.3 Hz之间，当系统表现为多群发电机之间的振荡时,振荡频率大致在0.4～0.7 Hz之间[5-6]。

根据低频振荡性质主要分为两种：一种是负阻尼低频振荡，负阻尼振荡是逐渐增幅过程，若没有人为干预，将持续保持增幅振荡，振荡的幅度越来越大，直到系统切机或失稳；另一种是强迫共振型的低频振荡，当扰动频率与系统自然振荡频率相同或接近时，产生共振，振荡振幅主要与扰动的幅度及系统阻尼水平有关，振荡过程中扰动源一直存在，振荡不会消失。

但由于两种振荡的表现形式很相似：

1)振荡的起始阶段都表现为增幅振荡；

2)增幅振荡都可能发展为等幅振荡。

这使得如何正确、快速判别振荡性质成为必须解决而又难于解决的问题。

2两种低频振荡响应特性

2.1　负阻尼低频振荡的响应特性

发电机采用经典二阶模型(假定E′恒定)，线性化的状态方程为

对于N维线性化系统状态方程：

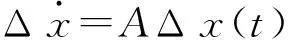
(1)

式中：Δx为增量形式的系统状态变量；A为系统状态矩阵。

对任一特征值λi，对非零向量φi∈CN×1和ψi∈CN×1(i=1,2,…,N)满足方程

(2)

则称φi和ψi分别为与矩阵A的特征值λi相对应的右、左特征向量[7-8]。

为了方便、简明地表达系统振荡响应的特征，分别定义特征根对角矩阵Λ、右特征向量矩阵φ、左特征向量矩阵ψ如下：

(3)

由式(2)可以看出，每个状态变量的变化率与所有的状态变量都线性相关。为了消去状态变量之间的耦合，引入新的状态变量Z，两种状态变量之间的模态坐标为

Δx=φZ

(4)

将式(4)带入式(2)中，可得

(5)

式(5)表示的N个解耦的一阶微分方程的解为

Zi(t)=Zi(0)eλit

(6)

由式(4)可得用ψi和Δx(0)表示的Zi(0)，即

(7)

将式(7)带入式(6)中，可得

(8)

将式(8)带入式(4)中，可得

(9)

式(9)即为多机系统负阻尼振荡响应的解析表达式。

可以看出，负阻尼振荡模式的系统中，相对振荡的机组，功角与转速将同时发生变化，不能通过振荡先后来识别振荡源。在多机系统中，右特征向量各分量的模值反映了相应机组参与振荡模式的强弱程度，分量的模值越大，该机组的振荡就越强；右特征向量各分量的相位反映了机组对该振荡模式的同调程度，负阻尼振荡的机组之间的相对相位将在振荡全程保持不变。

2.2　强迫低频振荡的响应特性

在包含N台发电机的多机系统中，由于主要关注振荡频率在0.1～2.5 Hz之间的机电模式，而它们主要由转子运动方程决定，所以可以只考虑转子运动方程。发电机采用经典二阶模型(假定E′恒定)，其线性化状态方程为

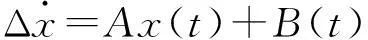
(10)

式中：x(t)为系统状态；A为系统状态矩阵；B(t)为扰动向量[9]。

假定初始时刻为t0，系统的初始状态为Δx(t0)。利用矩阵微分方程的初值问题定理，式(10)解的形式如式(11)所示，其中Δx1(t)表示系统的零输入(自由)响应，Δx2(t)表示系统的零状态(强迫)响应。

Δx(t)=Δx1(t)+Δx2(t)

(11)

假设系统的初始状态为Δx(t0)为0,利用积分公式：

(12)

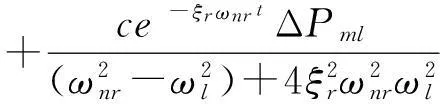
(13)

于是，可总结得到多机系统强迫功率振荡响应的特征如下：

1)强迫振荡响应是系统受到持续的周期性扰动后的响应。如果系统初始状态的变化量为0，该响应为系统的零状态响应；若系统的初始状态的变化量不为0，则响应中还包含系统的零输入响应成分；

2)多机系统强迫振荡的零状态响应是在所有扰动源的共同作用下、各阶振荡模式响应的叠加，由外施扰动源决定的强制(稳态)分量和由系统各阶振荡模式决定的自由(瞬态)分量组成；

3)当系统各阶振荡模式的阻尼为正时，无论扰动源的频率与系统振荡模式的频率相等与否，自由分量最终衰减为0，只剩下类似于无阻尼等幅自由振荡的强制分量。这表明，只有从包含自由分量的强迫振荡起振(瞬态)阶段的响应中，才有可能提取得到系统振荡的阻尼[10]；

4)某阶振荡模式下，不同系统状态响应之间的幅值比和相位差与系统初始条件和时间t无关，分别等于右特征向量响应分量的模值比和辐角差；

5)第i个状态变量的响应Δx2i(t)的幅值，与第l个机械功率扰动的幅值、第r阶振荡模式的阻尼大小有关；

6)第i个状态变量的响应Δx2i(t)的幅值，还与第r阶振荡模式的右、左特征向量的第i个和第l个分量的乘积|φirψrl|有关。这表明，响应的幅值与扰动源所在的机组参与强迫功率振荡的程度有很大关系，若机组参与该模式的程度较小，即使发生强迫功率振荡，振荡的幅值也不大。

3辨别两种振荡类型的判据

设在阻尼振荡频率为ωd的系统上施加持续周期性小扰动x1，其中B1为扰动幅值，ω为扰动频率，则系统的响应为

x(t)=x0+x1

(14)

式中：x0=B0sin(ωdt+φ)为强迫分量；x1=B1e-ξωntsin(ωdt+ψ)为自由分量。

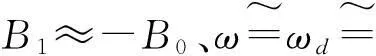
x=Bsin(ωt)-Beαtsin(ωt)

(15)

设t=ti时，x=x(ti)为振荡曲线x的上包络线上的一个极大值：

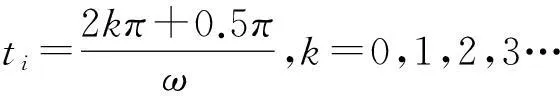
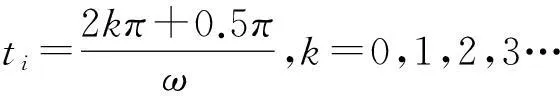
在x(t)取得最大值点tk依次对xmax(t)求一次、二次微分，可得：

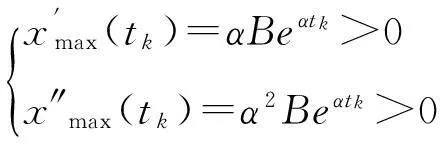
(16)

(17)

表1　基于起振阶段暂态响应

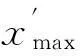
4实例验证

新疆某区域电网有3座火电厂，仅通过2回220 kV线路与主网相连。2014年9月20日，区域电网与主网相连的联络断面出现低频振荡，有功功率在43～91 MW 范围内摆动。通过调取PMU数据发现，A电厂、B电厂、C电厂机组均出现波动，其中A电厂机组波动最明显，有功出现30～50 MW波动，振荡频率约为0.5 Hz。图1为PMU记录的A电厂1号机组有功功率振荡曲线。

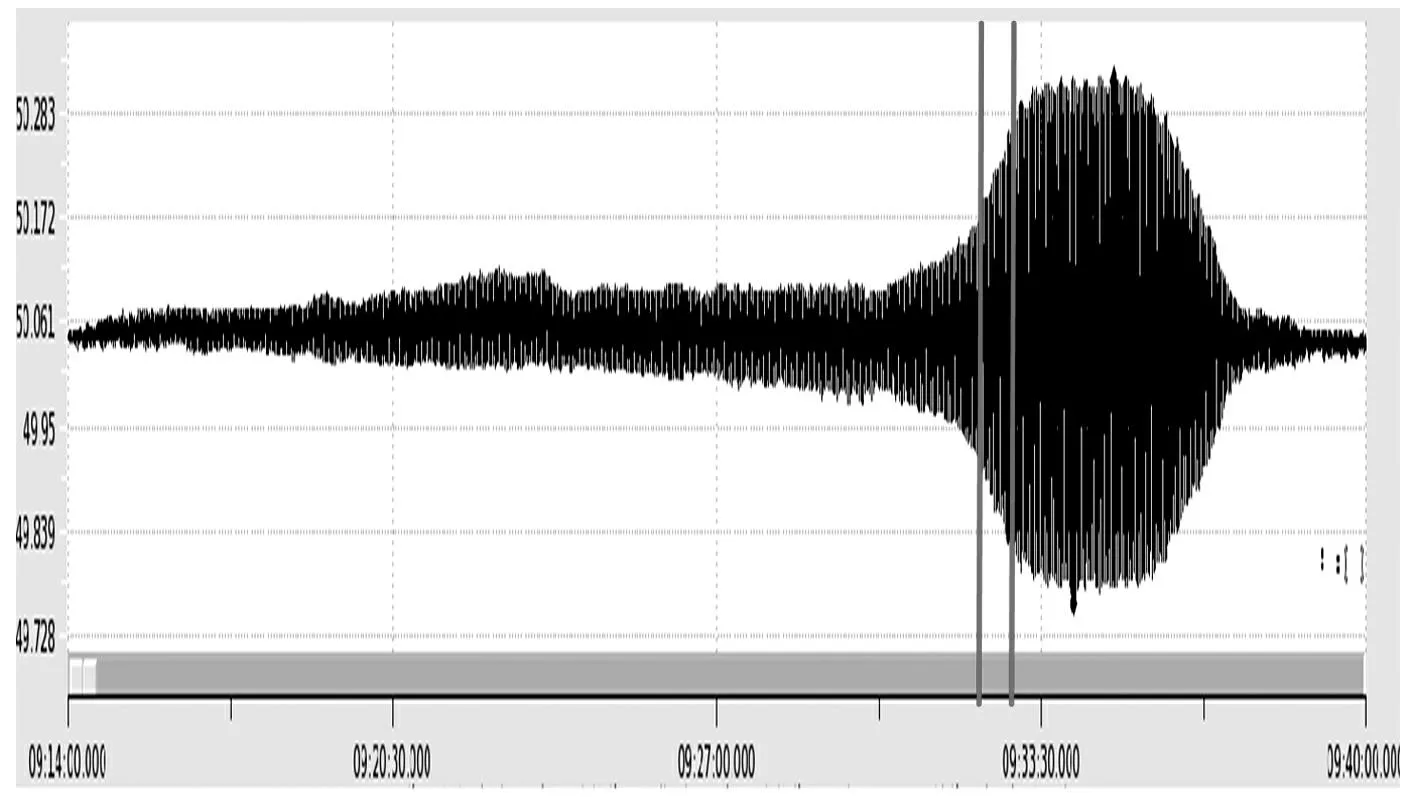
图1　A电厂1号机组有功功率振荡曲线

取振荡幅值较大的A电厂1号机组有功功率 PMU 录波曲线起振段的连续增幅振荡 7个周波的峰峰值进行分析，计算结果如表2所示。

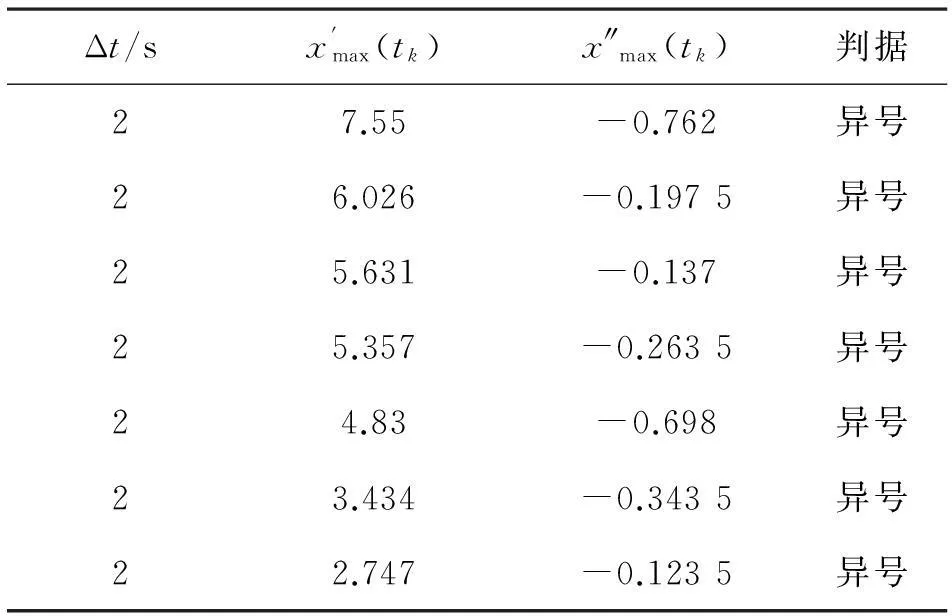
表2　用振荡类型判别法计算结果

5结论

通过对两种低频振荡响应特性进行研究，分析两种低频振荡的特征及区别，提出了基于起振阶段暂态响应包络线形状的振荡类型判别判据。该判据可以有效地利用WAMS、PMU的故障录波数据，快速准确地判别出功率振荡的起因是由于系统缺乏阻尼还是由于系统内存在强迫振荡源，从而有助于准确采取措施抑制振荡扩展，快速平息振荡，保证电网安全稳定运行。

参考文献

[1]王珍珍.调速系统引发低频振荡的机理及抑制措施研究[D].保定：华北电力大学,2014.

[2]王铁强,贺仁睦,王卫国,等.电力系统低频振荡机理的研究[J].中国电机工程学报,2002,22(2):21-25．

[3]刘辉,杨寅平,田云峰,等.电力系统强迫功率振荡实例及机理分析[J].电力系统自动化,2012,36(10):113-117.

[4]徐衍会,贺仁睦,韩志勇.电力系统共振机理低频振荡扰动源分析[J].中国电机工程学报,2007,27(17):83-87.

[5]杨慧敏.区域电网低频振荡特性分析与抑制方法的研宄[D].武汉：华中科技大学,2009.

[6]魏云冰,和萍,李山德,等.电力系统低频振荡机理及控制策略研究[J].山东科技大学学报,2008,2(3): 23-26.

[7]宋墩文,杨学涛,丁巧林,等.大规模互联电网低频振荡分析与控制方法综述[J].电网技术,2011(10):22-28.

[8]耿天翔,张竹竞,项丽,等.基于起振特性的强迫振荡扰动源定位及解列方案[J].电力系统保护与控制,2015(6):98-103.

[9]倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002.

[10]王茂海,孙昊.强迫功率振荡源的在线定位分析技术[J].中国电机工程学报,2014(34)：6209-6215.

中图分类号：TM712

文献标志码：A

文章编号：1003-6954(2015)04-0001-04

基金项目：国家自然科学基金项目(51267017)

作者简介：

周专(1987)，硕士，研究方向为电力系统规划、稳定与控制；

常喜强(1976)，硕士，研究方向为电力系统分析与控制；

张增强(1984)，硕士，研究方向为电力系统规划与分析。

(收稿日期：2015-04-29)

Abstract：With the large applications of the regional power grid interconnection, grid expanding and fast excitation systems, the dynamic stability problems of power system are more prominent, and gradually become the main factor influencing the grid security and power limit. Since a large number of dynamic elements being put into operation, the dynamic regulation performance is changed, and the poor dynamic stability will likely lead to low-frequency oscillation. Low-frequency oscillation can cause the system to have the oscillations of frequency, voltage, power and other electrical quantities in different degrees, the deteriorating interaction will eventually lead to system instability and splitting which will form large-scale blackouts. Therefore, low-frequency oscillation problem is getting more and more attention, and how to determine the oscillation properties correctly and quickly becomes a difficult problem. Therefore, the characteristics of negative damping oscillation and forced oscillation are studied, the oscillation distinguishing criterion for envelope shape based on transient response in start-up phase are proposed. It is verified by taking the low-frequency oscillation of one grid as example, and it shows that the proposed method can effectively determine the type of low-frequency oscillations, which has an important guiding significance for analyzing low-frequency oscillation and suppressing low-frequency oscillation in actual operation.

Key words：low-frequency oscillation; negative damping oscillation; forced oscillation; response characteristics