基于矩阵束算法的电压闪变检测新方法

罗志宏

(国网成都供电公司，四川 成都　610021)

基于矩阵束算法的电压闪变检测新方法

罗志宏

(国网成都供电公司，四川 成都610021)

摘要：随着电力系统冲击性负荷的增加，电网中存在的电压波动与电压闪变越趋严重。基于矩阵束算法提出了一种电压闪变参数检测新方法。该方法利用电压闪变信号模型的特殊性质，把它转换为矩阵间的特定关系，从而将难于处理的非线性求解问题简单化，不仅可以准确地提取闪变电压调幅波的频率和幅值，还可以获取相位信息。算法中引入矩阵低秩近似方法使得在求解广义特征值的时候，能更好地抑制噪声干扰，同时减少了计算量。分别对噪声背景下简单闪变和复杂闪变进行仿真分析，结果表明，该方法具有精度好、运算率高、抗噪性强等特点。

关键词：电压闪变；矩阵束算法；低秩近似；谐波

电压闪变的检测是通过准确提取电压波动信号，对波动信号进行频谱分析得到所含的各种低频谐波分量的频率和幅值[1-6]。目前常用的电压闪变测试方法有半波有效值法、平方检测法、全波整流法[7,8]。半波有效值法需将均方根值的计算时间准确地整定在半个工频周期之内，实现起来比较困难[9]；而平方检测法和整流检测法都需要设计频带很严格的滤波器来滤除工频和高次谐波分量。随着数学工具的发展，各种数学方法被广泛用于闪变检测。文献[10]提出基于快速傅里叶变换(fast fourier transformation，FFT)的波动电压检测方法，由于电压波动频率通常与基频不成整数倍关系，在考虑基频采样同步时难以做到对电压波动同步，所以利用FFT变换直接对波动电压进行分析，容易因采样不同步导致频谱混叠，从而影响测量结果的准确性。文献[11] 提出在FFT采样过程中使用跳跃式采样法，减少频谱泄漏引起的误差，但包络线提取时间较长。文献[12]、[13]提出了基于小波变换的电压闪变信号检测方法，但是这种检测方法略显复杂，且在实际应用中存在着小波基选择困难的问题。文献[14]将Hilbert变换用于电压闪变检测，但所分析信号必须为窄带信号，而实际闪变信号由于受到高次谐波等噪声的影响，并不满足这一特性。

除上述方法外，在电压闪变检测领域还可以采用矩阵束(matrix pencil, MP)方法提取闪变参数。

MP算法是1980年Y.B Hua和T.K Sarkar等人在前人经验的基础上针对极点提取问题而提出的一种方法。由于MP算法采用内积形式提高抗噪能力, 在数字信号处理方面获得了较好的效果[15]。此算法是非迭代算法的一种，它避免了迭代法的一些弊端，不存在累积误差的问题，而且运算量不高，是一种非常高效的数值计算方法[16]。将MP方法用于电压闪变检测，其基本思想是: 将采集到的电压闪变信号构造为Hankel矩阵，在求解广义特征值时引入SVD分解和矩阵的低秩近似方法抑制噪声干扰，从而达到信号参数的准确求取的目的。通过仿真分析发现该方法不仅可以较准确地提取闪变电压调幅波的频率和幅值，还可以得到相位信息，从而为电压闪变检测提供了一种新的思路。

1电压闪变信号数学模型

电压的波动和闪变特征通过调幅波[17]反映出来，故对调幅波参数的求取等同于对电压闪变参数的提取。一般电压波动幅值范围为工频载波电压幅值的0%～10%。电压闪变有周期性和非周期性之分，其中周期性电压闪变对人们生产生活影响较大，故这里主要研究周期性闪变参数的提取。通常电压闪变信号中包含谐波，为使分析简化一开始先不考虑谐波，在后面的部分再考虑谐波。如果忽略谐波成分，电压闪变信号u(t)可表示为条幅信号Ai对已工频正弦信号的线性振幅调制。

(1)

式中：A0、f0、θ0分别为基波电压的幅值、频率和初始相位；Ai是频率为fi、相位为θi的调幅波分量的幅值。通过三角函数分解将式(1)展开得

u(t)=A0cos(2πf0t+θ0)+

(2)

可以看出：经展开后的电压闪变信号，在频域内总是以工频为中心，在工频两侧呈对称分布。(f0-fi)和(f0+fi)对应的分量称为边频分量。通过对u(t)的直接检测可得到边频分量的参数，从而再间接求得电压闪变模型中调幅波电压的幅值、频率和相位信息。

2矩阵束算法基本原理

MP算法的计算步骤简介如下[16,18]：由实测数据或仿真数据y(kΔt)(k=1,2,……,N-1),构造Hankel矩阵Y为

(3)

式中：Dk=[y(k),y(k+1),…y(N-L+k-1)]T。

式中：L为矩阵束参数，合理地选取L可以减小数据中的噪声干扰，通常取值范围在N/4～N/3之间。

对Y作奇异分解，Y=U∑VT得到(N-L)×(L+1)阶对角阵∑，其元素σi为Y矩阵的第i个奇异值。

如果测量数据不含噪声，Y有M个非零奇异值，且σ1≥σ≥…≥σM，此时Y的秩等于M。但在实际测量中，由于存在噪声和模型误差，使真实的极点产生误差，并产生多余的虚假极点。此时，对奇异值进行截取，只保留其中M个最大的奇异值，可以有效减小噪声对参数估计精度的不良影响。若同时满足下面2个条件：1)从第M+1个奇异值σi+1开始不再发生跳跃；2)σi/σi+1≥μ(μ为阈值)，则可以把最大下标i记为最大模态数M。

由矩阵V的M个主奇异向量构成的滤波矩阵：V′=[v1,v2,…vM]。构造2个(N-L)×L阶矩阵Y1和Y2为

(4)

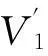
由Y1和Y2构造矩阵束Y2-λY1,通过整理、计算可求解矩阵G=Y+1Y2的特征值(其中Y+1为Y1的伪逆矩阵)。在估计出最大模态M和所有极点zi(i=1,2,…,n)后,留数Ri可利用最小二乘法计算得到，具体式如下：

(5)

计算出反映各分量特征的量，计算式为

(6)

式中,Ai、θi、αi、ωi为对第i个模态的幅值、初相位、衰减因子和角频率。

MP算法通过抽样构造Hankel矩阵、降秩、极点提取、极点个数提取, 最后利用最小二乘法得到留数, 实现了非线性问题的线性求解。

3仿真实验

3.1　理想信号算例

在实际运行中，电压闪变参数的准确参数值是无法预知的, 参数的理论计算值和测量值都是对它的近似描述, 所以参数测量值的误差大小很难定量描述。为了验证所提出的方法在电压闪变参数估计方面的有效性，以下面含有单个频率闪变的理想信号为例进行分析。

u(t)=[1+0.06cos(50πt+π/4)]×

[cos(100πt+π/6)]

(7)

由于在实际测量信号中含有高频率的噪声，故对上述理想信号中加入信噪比为30 db高斯白噪声，该电压闪变信号时域波形如图1所示。在Matlab下进行仿真，信号采样频率为1 kHz，采样时间为0.4 s。采用MP方法对上述信号进行分析时，首先对由采样信号形成得Hankel矩阵进行奇异值分解，其奇异值柱状图如图1所示。从图1中可看出从6阶到7阶处奇异值有跳跃，比值很大；并且从第7阶开始奇异值不在发生跳跃，因此确定系统的阶数是6。利用MP方法提取的参数如表1 所示。

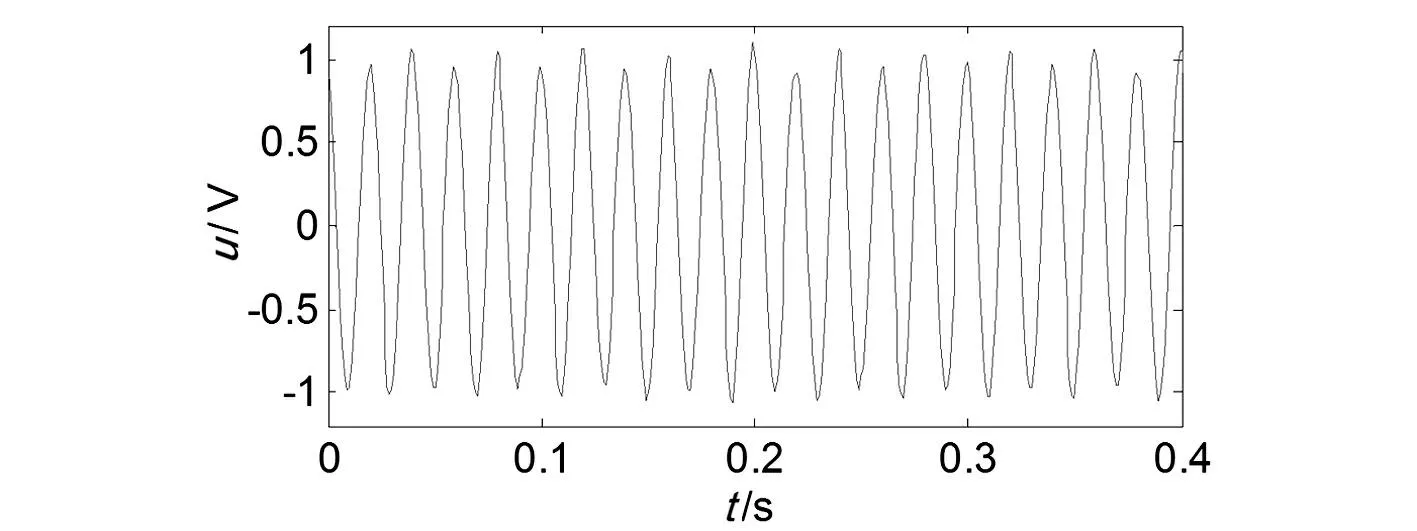
图1　简单闪变信号波形

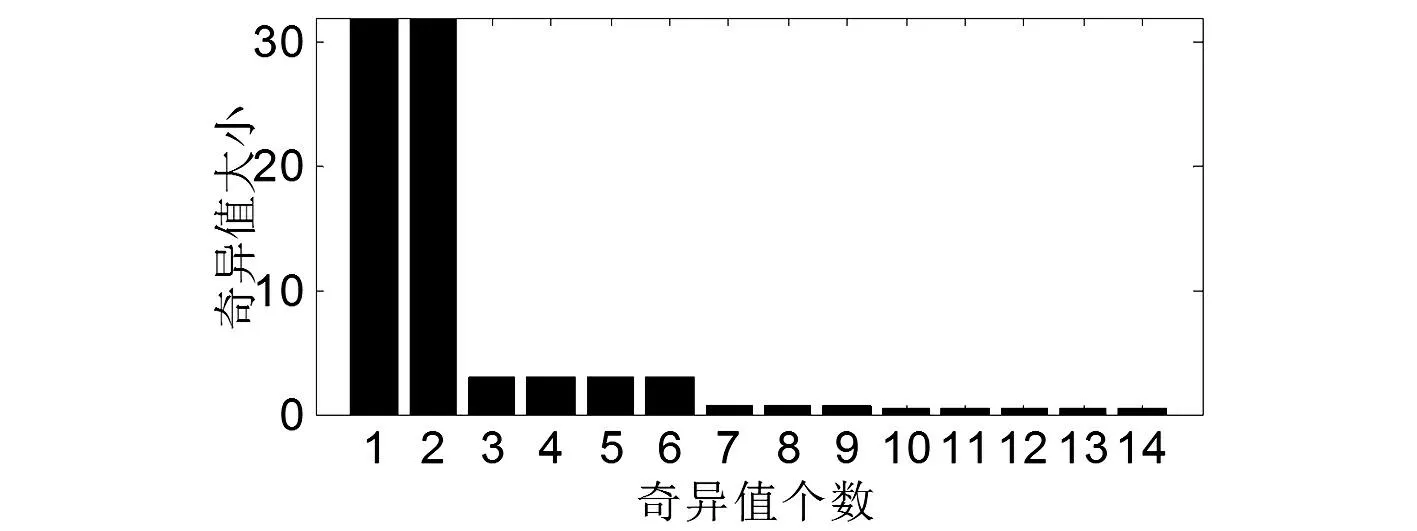
图2　理想信号算例奇异值柱状图

参数分量幅值/V频率/Hz相位/(°)基频0.996049.999830.0611边频分量10.029375.096372.7069边频分量20.031524.9887-15.3452

根据表1提取的参数和式(1)、(2)可计算出调幅波参数，与理想参数的比较如表2所示。可以看出在噪声为30 db情况下，辨识非常准确，调幅波的幅值和频率的误差分别为1.333%、0.215%，误差较小。为验证该算法的抗噪性，表2还给出了噪声为40 db和25 db时调幅波的检测值。由表2分析可知，噪声为40 db时调幅波参数的最大误差不超0.5%，随着噪声的增大，辨识结果的误差也逐渐增大，但都在合理的范围之内。仿真结果证明在简单闪变情况下MP方法具有较高的抗噪能力和检测精度。

表2　理想信号算例参数及检测值

3.2　含谐波信号算例

闪变信号中往往包含多频闪变，并存在谐波污染，在检测信号中加入幅值为0.08、频率为10 Hz的调幅波和幅值为0.1、频率为100 Hz的谐波信号，该复杂闪变信号为

u(t)=[1+0.06cos(50πt+π/4)+

0.08cos(20πt)]×[cos(100πt+π/6)+

0.1cos(200πt+π/3)]+e(t)

(8)

该复杂闪变信号波形如图3所示。图4为Hankel矩阵分解后的奇异值变化曲线。根据奇异值变化曲线图，将Hankel矩阵有效秩M定为12是合理的。MP 方法提取的参数如表3 所示。由表3可知，MP方法提取了基波、谐波以及与50 Hz对应的4个边频分量，但没有提取谐波的边频分量。这是因为谐波的边频分量幅值很小，对应的奇异值也很小，进行低秩近似时，MP算法已将其视作噪声滤除了。

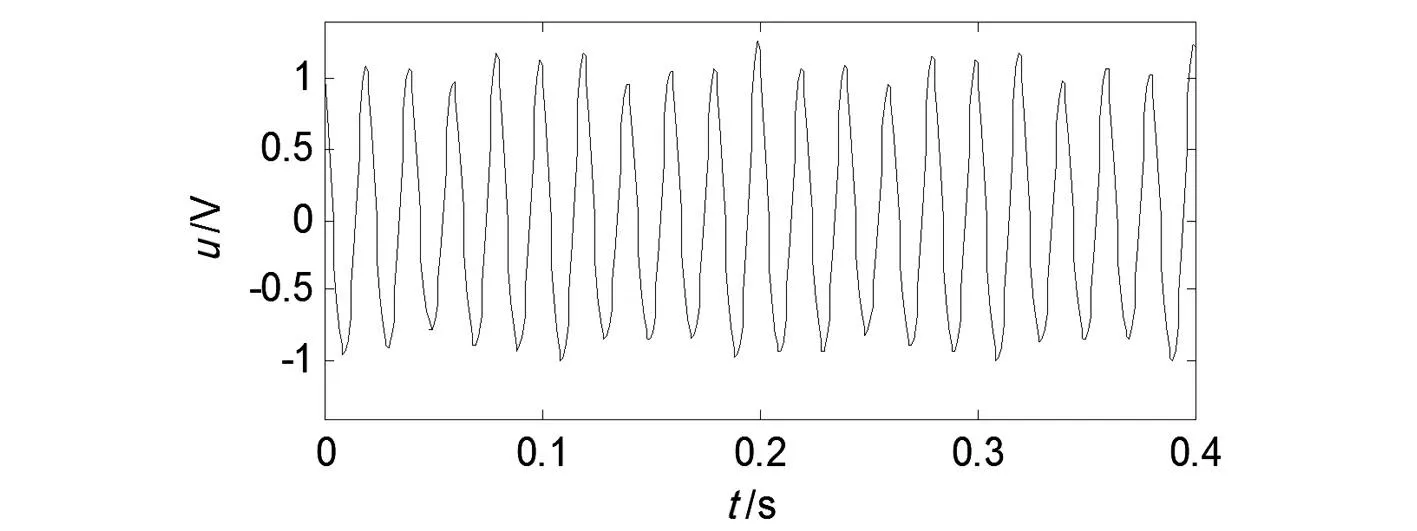
图3　复杂闪变信号波形

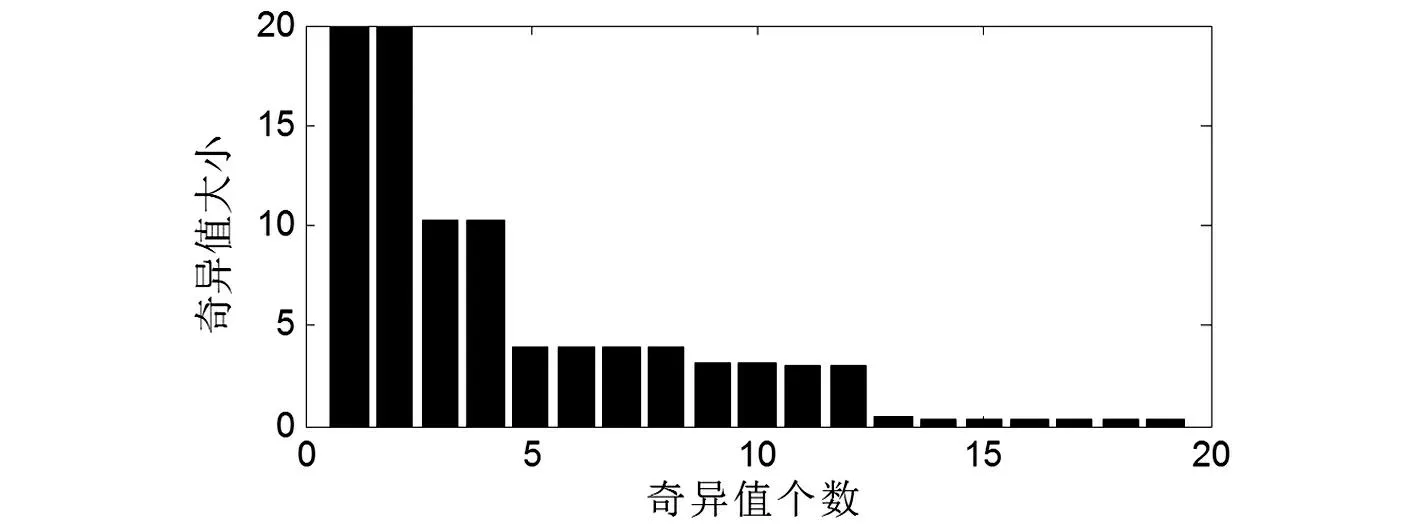
图4　含谐波信号算例奇异值柱状图

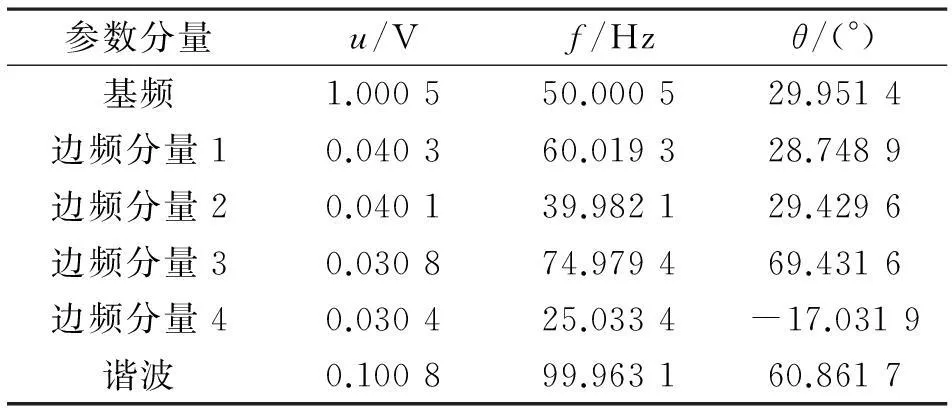
参数分量u/Vf/Hzθ/(°)基频1.000550.000529.9514边频分量10.040360.019328.7489边频分量20.040139.982129.4296边频分量30.030874.979469.4316边频分量40.030425.0334-17.0319谐波0.100899.963160.8617

表4给出了计算参数与理想参数的比较。从表4的最终计算参数来看，谐波对计算结果准确性不会产生较大影响，辨识参数的最大误差仅为2 %，可见在复杂闪变情况下MP方法也同样具有较高的抗噪能力和检测精度。

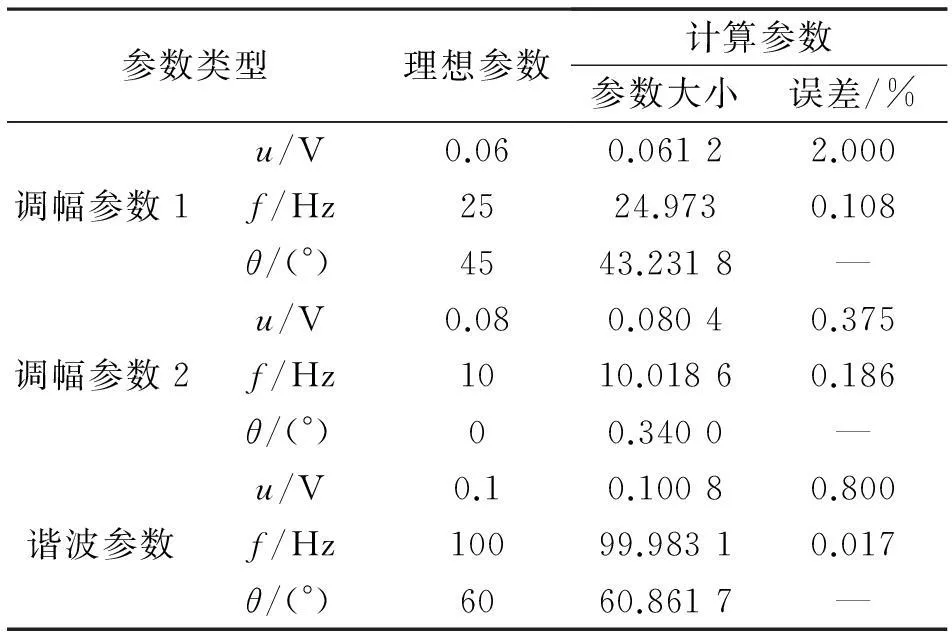
表4　含谐波信号算例参数及检测值

4结论

1)将MP算法用于电压闪变参数的提取，利用电压闪变信号模型的特殊性质，把它转换为矩阵间的特定关系；从而将难于处理的非线性求解问题简单化，不仅可以较准确地提取闪变电压调幅波的频率和幅值，还可以获取相位信息。

2)该方法将在求解广义特征值的时候通过低秩近似方法减小了噪声干扰，并提高了计算效率。

3)噪声背景下的简单电压闪变和包含谐波及多调幅的复杂电压闪变的仿真结果，验证了所提方法的可行性和有效性，为电压闪变参数提取提供了一种新的思路。

参考文献

[1]孙树勤. 电压波动与闪变[M]. 北京: 中国电力出版社, 1998.

[2]Toivonen L, Morsky J．Digital Multirate Algorithms for Measurement of Voltage, Power and Flicker[J]. IEEE Trans. on Power Delivery, 1995, 10(1): 116-126.

[3]郭上华, 黄纯, 王磊，等. 电压波动和闪变的检测与控制方法[J]. 湖南电力,2003，23(3):8-11.

[4]魏晓璞，徐永海，郭春林，等．基于Hilbert 变换与Pisar

enko谐波分解的电压闪变参数估计[J]．电力系统保护与控制，2010 ，38(6)：26-29．

[5]王志群，朱守真，周双喜．Hilbert 变换求取电压闪变有关参数[J]．电力系统自动化，2004，28(5)：34-37．

[6]Soliman S A，El-Hawary M E．Measurement of Power Systems Voltage and Flicker Levels for Power Quality Analysis： A Static LAV State Estimation Based Algorithm[J]．International Journal of Electrical Power and Energy Systems，2000，22(6)：447-450．

[7]郭上华, 黄纯, 王磊，等. 电压波动和闪变的检测与控制方法[J]. 湖南电力,2003,23(5):8-11.

[8]肖冰，梁军，路平，等．Hilbert 变换在电压闪变检测中的应用[J]．继电器，2005 ，33(15)：62-65．

[9]李天云，祝磊，党国营，等．总体最小二乘-旋转矢量不变技术在电压闪变参数提取中的应用[J]．电网技术，2009，33(13)：58-63．

[10]Srinivasan K．Digital Measurement of the Voltage Flicker[J]．IEEE Trans. on Power Delivery，1991，6(4)：1593-1598．

[11]Wu Chi-Jui, Chen Yu-Jen. A Novel Algorithm for Precise Voltage Flicker Calculation by Using Instantaneous Voltage Vector[J]. IEEE Trans. on Power Delivery,2006,21(3):1541-1548.

[12]杨坤, 杨洪耕. 基于小波测位的闪变检测算法及其实现[J].继电器,2004,32(21):48-52.

[13]刘会金, 吴玉蓉, 熊玲玲. 基于Daubechies 小波的多分辨分解在电压闪变信号分析中的应用[J]. 继电器,2004,32(13):6-11.

[14]舒泓，王毅. 基于数学形态滤波和Hilbert 变换的电压闪变测量[J]．中国电机工程学报，2008，28(1)：111-114．

[15]朱瑞可，李兴源，赵睿，等．矩阵束算法在同步电机参数识中的应用[J]．电力系统自动化，2012，36(6)：52-85．

[16]朱瑞可，王渝红，李兴源，等．基于矩阵束算法的谐波和间谐波参数估计[J]．华东电力，2012，40(3)：388-391．

[17]张君俊，杨洪耕．TLS-ESPRIT法在电压闪变参数估计中的应用[J]．电力系统保护与控制，2009，37(9)：44-48．

[18]李宽，李兴源，赵睿．基于改进矩阵束的高压直流次同步振荡检测[J]．电网技术，2012，36(4)：128-132．

中图分类号：TM866

文献标志码：B

文章编号：1003-6954(2015)04-0066-04

作者简介：

罗志宏(1984)，硕士研究生，研究方向为电力系统稳定与控制。

(收稿日期：2015-03-30)

Abstract：Voltage fluctuation and voltage flicker have become a serious problem with the rapid increase of impulse load in power system. Based on matrix pencil algorithm, a new method to identify voltage flicker parameters is proposed. This method uses the special property of voltage flicker signal model and converts it to the special relationship between matrixes. As a result, the nonlinear question which is difficult to be processed will be simplified. This method not only can accurately extract the frequency and amplitude of flicker voltage wave, but also can get accurate information of phase. And the noise effect is restrained because of the low-rank approximation method when the generalized eigenvalue is to be solved. At the same time, the calculated amount is reduced. The simple flicker and complex flicker which are under the back ground of noise are analyzed respectively and the simulation results show that the proposed method has high precision, fast operation efficiency and strong anti-nose capacity.

Key words：voltage flicker; matrix pencil algorithm; low-rank approximation; harmonics