基于PMU/SCADA混合量测状态估计及不良数据检测方法

许　勇

(西南交通大学电气工程学院,四川 成都　610031)

基于PMU/SCADA混合量测状态估计及不良数据检测方法

许勇

(西南交通大学电气工程学院,四川 成都610031)

摘要：充分利用PMU量测及SCADA量测值，讨论并发展了一种基于PMU/SCADA混合量测的电力系统状态估计及不良数据检测方法。首先利用快速分解状态估计得到估计结果，再将状态估计结果和PMU量测值进行二次线性状态估计。同时利用二次线性状态估计更新残差协方差矩阵的方式来对SCADA量测量中的关键量测量是否存在不良数据进行检测。最后采用IEEE 30节点系统验证了该方法的有效性。

关键词：电力系统；相量测量单元；混合状态估计；不良数据检测

0引言

电力系统状态估计(state estimator)是电力调度中心能量管理系统(energy management system,EMS)非常重要的组成部分，更是电网安全评估、预防控制和运行分析等各种高级应用的基础[1]。其基本原理是根据量测数据的冗余度，按照最佳估计准则对生数据进行相关处理，使得量测数据更好的接近真实值。

近年来，同步相量测量单元(phasor measurement unit,PMU)相对于数据监控及采集系统(SCADA)能对测量节点提供更高精度的相量测量。但是PMU量测装置成本较高，不能在短时间内将SCADA完全取代，这将会与SCADA长期共存[2]，因此，将SCADA和PMU量测相结合进行混合状态估计是一种比较理想的方法。目前相关研究已经取得了一定的成果[3-6]，文献[7]提出了二次状态估计的思想，这对提高状态估计的精度有明显提高，但是耗时较长，通过对非线性状态估计进行优化的方法，这样既可以提高状态估计的精度、缩短估计运行时间，又能很好地满足电力系统实时性的要求。

评价一种状态估计算法是否优良，不仅要保证该算法能够高效快速地估计出电力系统中状态量的值，同时具备一定的不良数据处理能力，以确保状态估计结果的准确性。首先对混合量测电力系统状态估计算法进一步探讨，并提出了一种对SCADA量测量中的关键量测量出现不良数据的检测方法，最后，通过实验验证了该方法的有效性。

1混合量测线性状态估计算法

1.1　非线性状态估计模型

快速解耦状态估计算法是将加权最小二乘法进行了改进，其量测量是通过SCADA获取，其数学模型为

(1)

式中：Za和Zr分别为电压幅值和电压相角的量测数据；υa和υr分别为电压幅值和电压相角的量测误差。

由于在电网中电压幅值U主要受无功功率Q的影响，节点相角θ主要受有功功率P的影响，因此，Za主要是支路有功功率或有功注入量测量，Zr主要是支路无功功率或无功注入量测量。

同样地，雅可比矩阵可改写为

(2)

同时，权值矩阵也可以分解为有功和无功两部分，即

(3)

由于节点电压幅值主要受无功功率影响，节点电压相角主要受有功功率影响，式(2)中Har≈0及Hra≈0。于是信息矩阵可以写成

(4)

由于信息矩阵一般为稀疏矩阵，由潮流计算可得

(5)

将式(4)带入式(5)右端，可得迭代修正方程为

AΔθ(l)=a(l)

BΔu(l)=b(l)

(6)

式中：

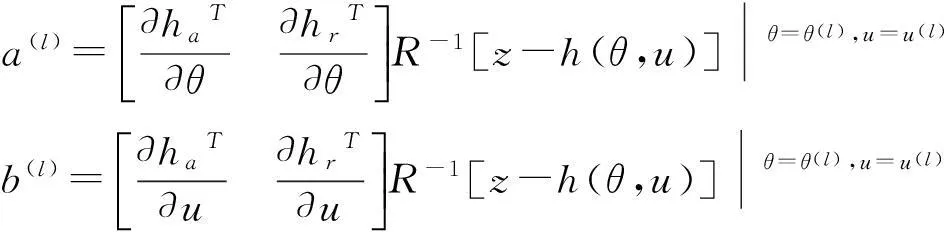
(7)

1.2　线性状态估计模型的建立

将电力系统各节点和支路的实部电流和虚部电流及快速解耦状态估计结果用直角坐标的各节点电压向量表示，然后可以得到电力系统线性量测方程组，其数学模型为

(8)

由于雅可比矩阵高度稀疏，且与系统拓扑及参数无关，从而大大简化了线性状态估计的计算量。对于上面的量测方程，由加权最小二乘原理可以求得线性状态估计计算式为

(9)

(10)

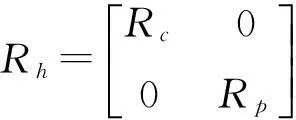
2不良数据检测

当系统量测冗余度较低时，系统中可能存在关键量测量，而关键量测量不是一个冗余量测量。如果将关键量测量从量测系统中删除，将导致系统不可观测，因此，利用PMU量测信息来提高整个系统的量测冗余度并对SCADA量测中关键量测量出现不良数据时进行检测。检测的基本公式为

(11)

式中：

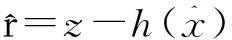
(12)

D=cov(r)=R-H(HTR-1H)-1HT

(13)

1) 非关键量测量的不良数据检测

(14)

Dc=cov(r)=Rc-Hc(HcTRc-1Hc)-1HcT

(15)

式中：Rc和Hc分别是来自传统状态估计的量测误差的协方差矩阵和雅克比矩阵。

2) 关键量测量的不良数据检测

(16)

D=cov(r)

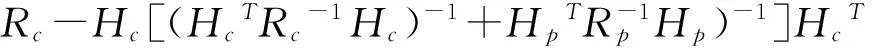
(17)

式中：Rp和Hp分别是混合量测状态估计的量测误差的协方差矩阵和雅克比矩阵。

3算例分析

采用IEEE 30节点系统对该算法进行算例分析。PMU装置装设位置为8、9、12、24、25节点，如图1所示。仿真软件选用Matlab 7.0。其中，SCADA量测值和PMU量测值都是在潮流计算结果的基础上分别叠加10-2和10-4的正态分布随机量测误差，没有加入PMU量测量之前，整个SCADA量测系统是完全可观测的，并且冗余度的比例保持在1.1到1.3之间。所有的检测情况都将检测的阈值设置为2.81(99.5%的置信度)。

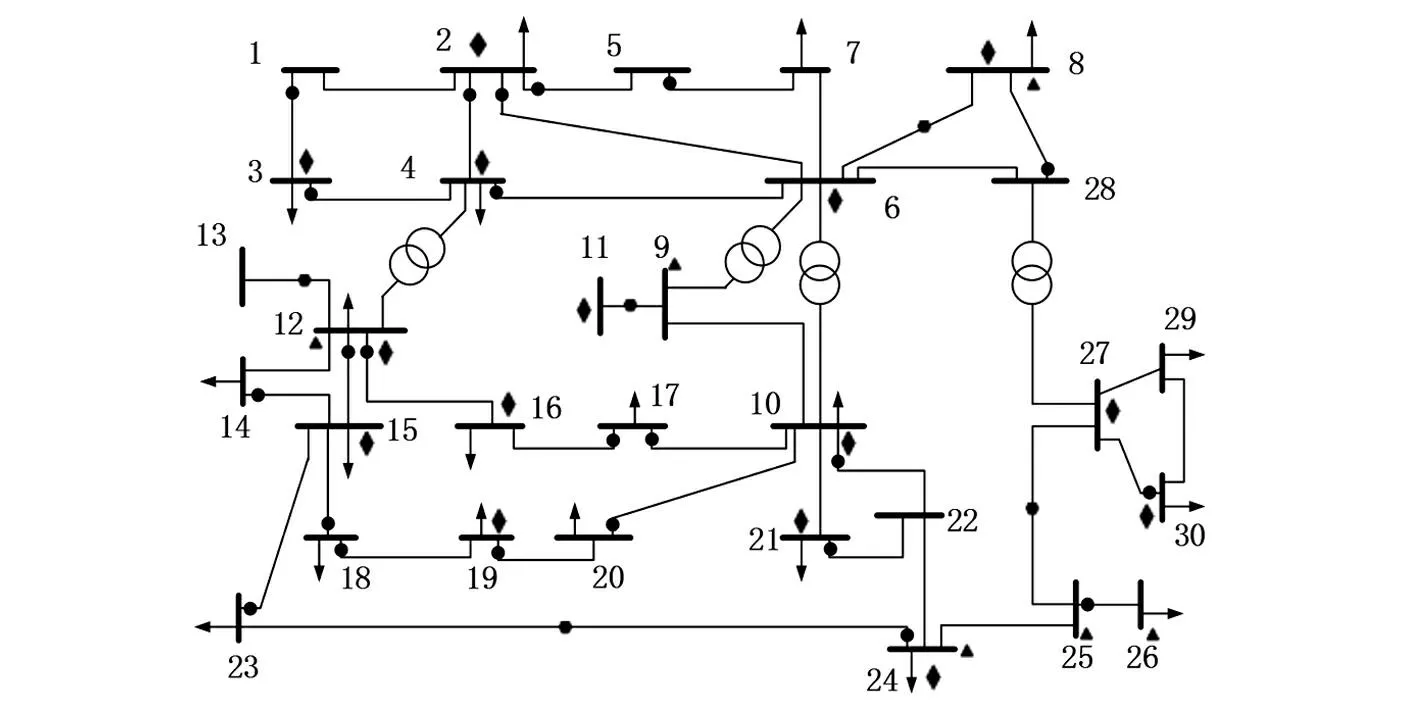
注：SCADA量测中 ●为支路潮流有功/无功功率； ◆为节点注入有功/无功功率； ■为节点电压幅值;PMU量测中 为支路电流相量； ▲为节点电压相量。图1　IEEE 30节点网络系统接线图

本次实验主要对以下几种情况进行了如下分析。

1)状态估计结果对比

图2和图3分别给出了所提方法、加权最小二乘算法、潮流真值的电压幅值和相角的对比结果。

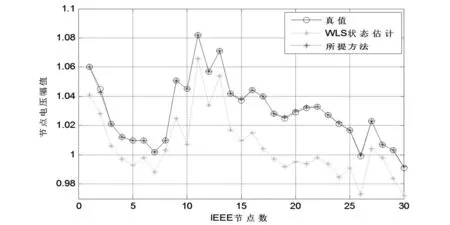
图2　IEEE 30节点系统的电压幅值对比结果

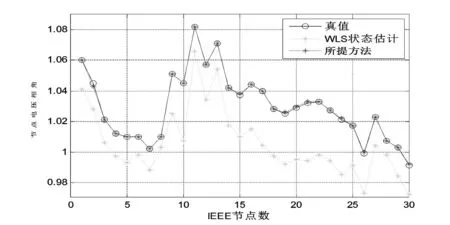
图3　IEEE 30节点系统的电压相角对比结果

为了更加清晰地对比所提方法，图4、图5给出了所提方法和加权最小二乘算法与真值的绝对误差对比结果。

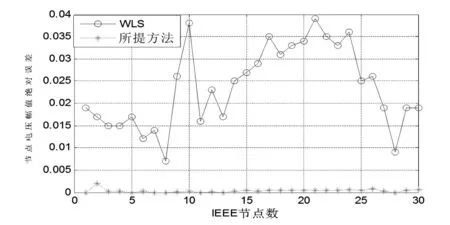
图4　IEEE 30节点电压幅值绝对误差对比结果

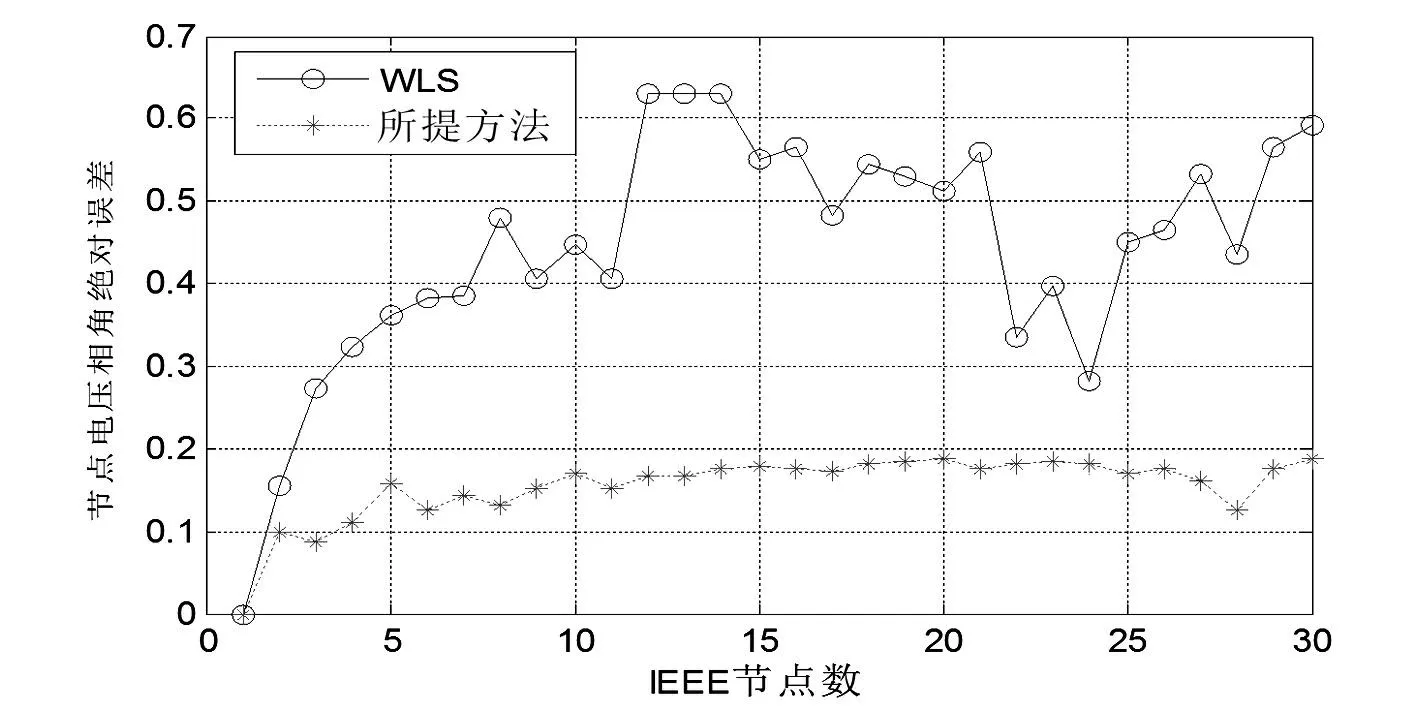
图5　IEEE 30节点电压相角绝对误差对比结果

通过图4、图5绝对误差对比结果可以得出，所提出的方法对状态估计结果有明显的提高。

2)非关键量测量的检测

在SCADA量测量中，对非关键量测量节点有功功率P4设置30%的量测误差值。通过表格将较大的几个量测残差值列出来，如表1所示。

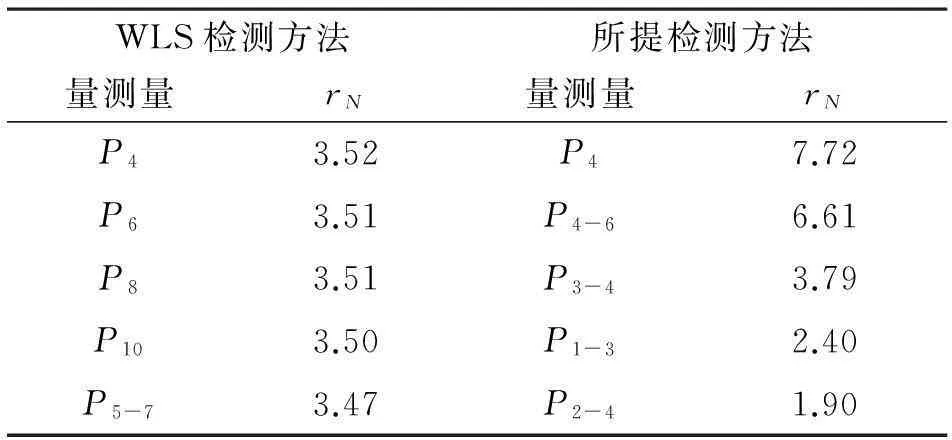
表1　IEEE 30节点系统非关键量测量标准化残差值

为了进一步对比其他量测残差值的大小，图6、图7将所有的SCADA量测量的标准化残差值用直方图展示出来。

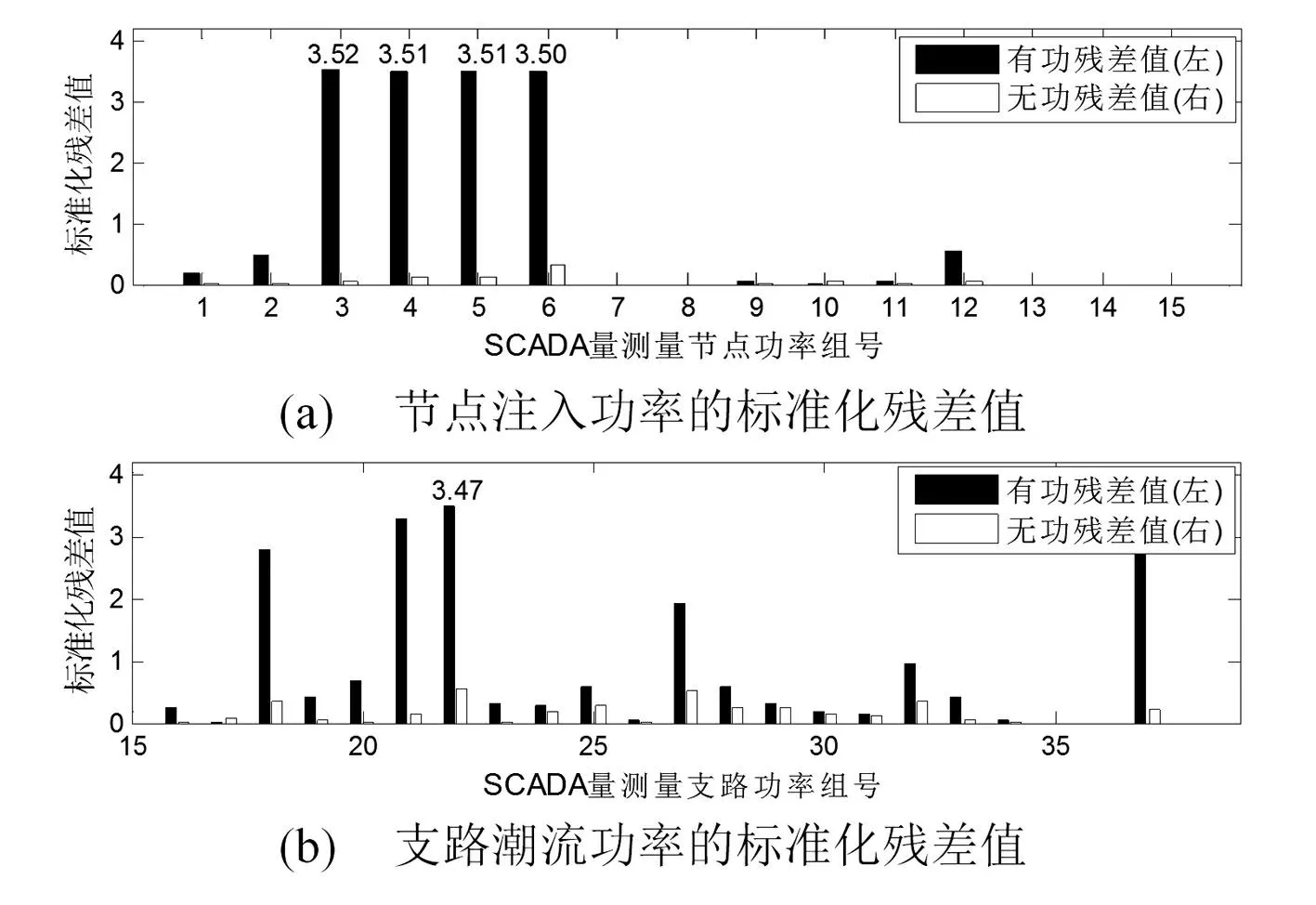
图6　WLS状态估计后的SCADA非关键量测量标准化残差值

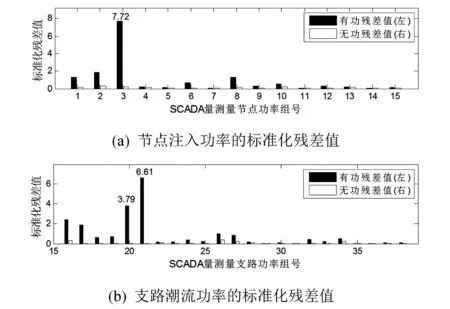
图7　混合量测状态估计后的SCADA非关键量测量标准化残差值

对于非关键量测量中的不良数据，采用所提方法和WLS状态估计算法都能将其检测出来。

3)关键量测量的检测

在SCADA量测量中，对关键量测量支路潮流无功功率Q24设置30%的量测误差值，并将较大的几个残差值对应的量测量用列出来，如表2所示。

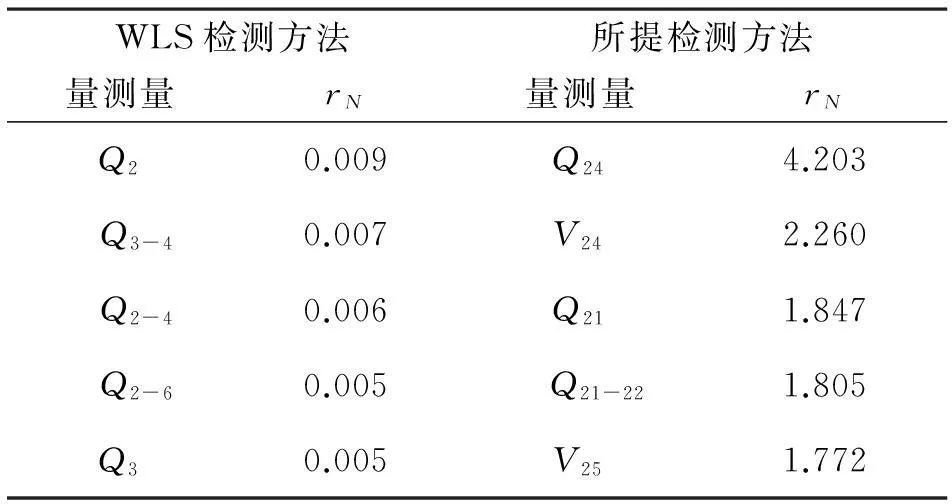
表2　IEEE 30节点系统关键量测量标准化残差值

通过表2可以看出，通过加权最小二乘状态估计算法计算各个量测量的标准化残差值，所有量的测量残差值都在检测阈值范围之内，无法将不良数据检测出来，而通过混合量测状态估计对残差协方差矩阵更新后，可以看出量测量Q24的标准化残差值大于阈值2.81，能够被检测出来。

为了对比其他残差值的大小，图8、图9将所有的SCADA量测量的标准化残差值用直方图展示出来。

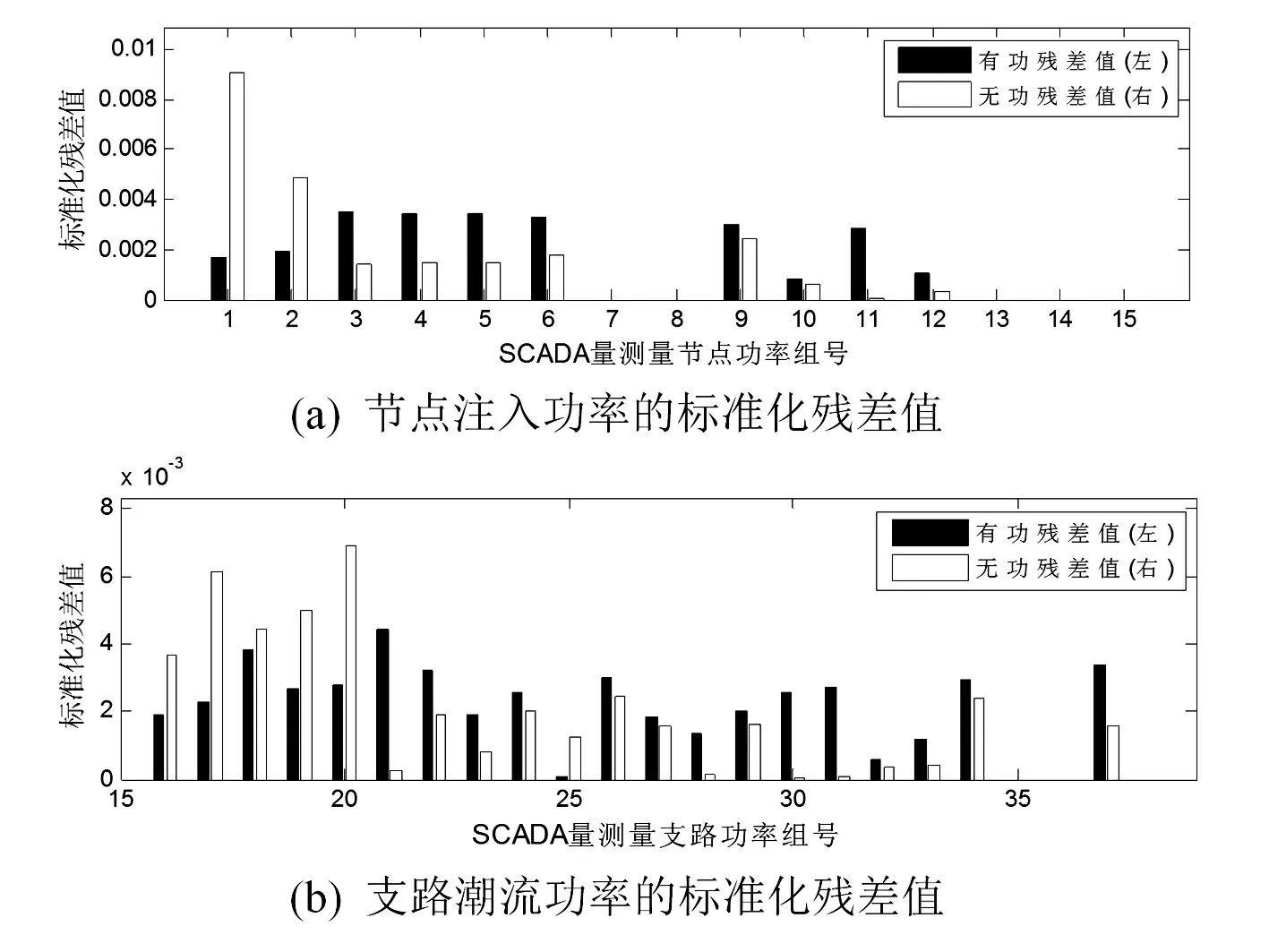
图8　WLS状态估计后的SCADA关键量测量标准化残差值

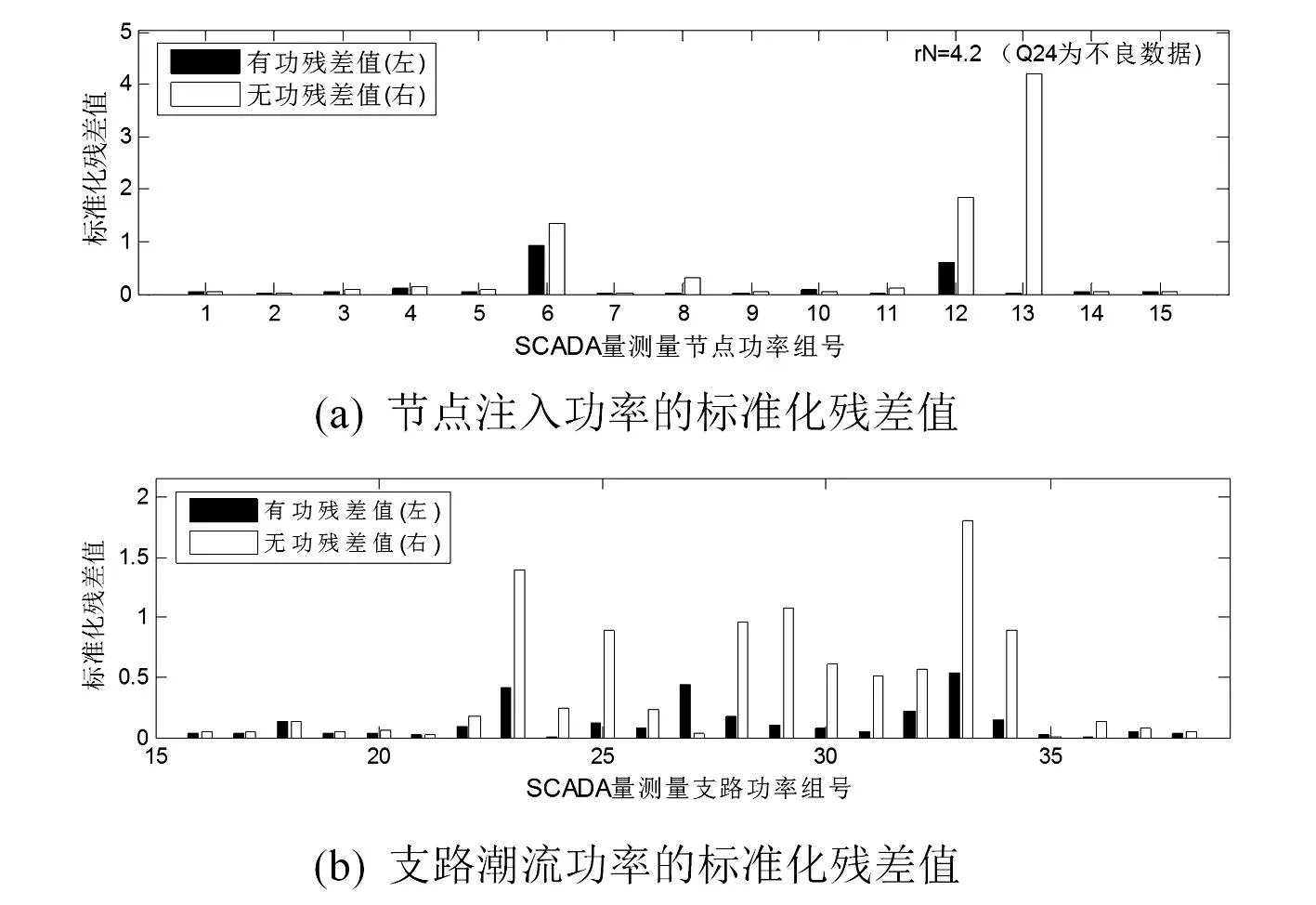
图9　混合量测状态估计后的SCADA关键量测量标准化残差值

通过PMU量测量对残差协方差矩阵更新后，当SCADA量测量中的关键量测量出现不良数据时，PMU量测量的标准化残差值也将改变，如图10所示。

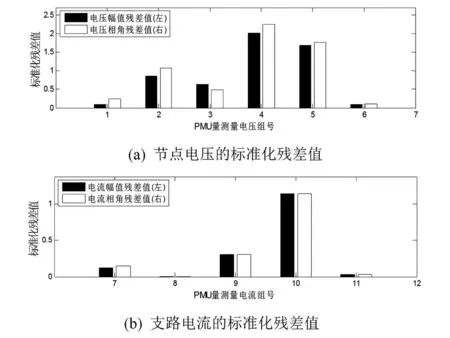
图10　混合量测状态估计后的PMU量测量标准化残差值

根据实验结果分析可知，所提状态估计方法与仅有SCADA量测量的状态估计的区别主要包括：1)量测量的冗余度不同：传统状态估计的量测量只是通过SCADA量测系统获得，冗余度较低，系统中存在关键量测量；而混合量测状态估计的量测量包含SCADA量测量和PMU量测量，冗余度高，不存在关键量测量。2)估计方式不同：传统状态估计只通过非线性状态估计获得估计结果，估计结果精度不高；而混合量测状态估计方法将利用非线性状态估计结果和PMU量测信息进行二次线性状态估计，状态估计结果的精度大大提高。

混合量测状态估计方法的优点主要包括：状态估计结果精度高，能够检测关键量测量中出现的不良数据。不足之处在于需要进行两次状态估计，需要多耗费一些时间。

4结语

充分利用PMU量测及SCADA量测值，讨论并发展了一种基于PMU/SCADA混合量测的电力系统状态估计及不良数据检测方法。特别是当SCADA量测系统的关键量测量出现不良数据时，通过PMU量测量增加系统冗余度，同时利用二次线性状态估计更新残差协方差矩阵的方式来对SCADA量测量中的关键量测量中的不良数据进行检测，通过IEEE 30节点系统对该方法进行了试验，效果较好。

参考文献

[1]李从善, 刘天琪, 李兴源, 等. 用于电力系统状态估计的WAMS/SCADA混合量测数据融合方法[J]. 高电压技术, 2013, 39(11)：2686-2691.

[2]刘晓义, 宋佳音, 蒋辉雄, 等. 基于PMU/SCADA混合量测的电力系统状态估计[J]. 电测与仪表,2012,49(559)： 11-15.

[3]薛辉, 贾清泉, 王宁, 等. 基于PMU量测数据和SCADA数据融合的电力系统状态方法[J]. 电网技术, 2008,32(14)：44-49.

[4]李强, 周京阳, 于尔铿, 等. 基于混合量测的电力系统状态估计混合算法[J]. 电力系统自动化, 2005,29(19)：31-35.

[5]G. N. Korres, N. M. Manousakis. State Estimation and Bad Data Processing for Systems Including PMU and SCADA Measurements[J]. Electric Power Systems Research，2011(81)：1514-1524.

[6]P S Castro Vide, F P Maciel Barbosa, I M Ferreira. Combined Use of SCADA and PMU Measurements for Power System State Estimator Performance Enhancement[C]. Energetics (IYCE), Proceedings of the 2011 3rd International Youth Conference on. IEEE, 2011: 1-6.

[7]R. F. Nuqui, A. G. Phadke. Hybrid Linear State Estimation Utilizing Synchronized Phasor Measurements[J]. Power Tech, 2007 IEEE Lausanne，1665-1669.

中图分类号：TM7

文献标志码：A

文章编号：1003-6954(2015)04-0051-05

作者简介：

许勇(1988)，硕士研究生，主要研究方向为电力系统状态估计。

(收稿日期：2015-03-09)

Abstract：A new state estimation method for bad data detection and identification based on PMU/SCADA hybrid measurement is presented by making full use of PMU and SCADA measurements. At first, the rapid decomposition state estimation is done on the condition of taking nodes' status values measured by SCADA, and then the linear state estimation is done with both state estimation results and PMU measurements. Meanwhile, whether there is bad data or not in critical measurements in SCADA is detected and identified by using the second linear state estimation to update the residual covariance matrix. Finally the effectiveness of the model is verified by the numerical calculation results of IEEE-30 bus system.

Key words：power system; phasor measurement unit (PMU); hybrid state estimation; bad data detection