股指期货最优套保比率的估计与套保绩效分析
2015-12-30西南财经大学统计学院成都611130
■ 林 睿(西南财经大学统计学院 成都 611130)
引言
上世纪70年代的布雷顿森林体系的崩溃和石油危机的爆发使得国际金融市场交易变得频繁起来,国际间的金融贸易交易趋于自由化,国与国之间的金融贸易管制不再那么严格,资本的流动也变得宽松起来,在这种大环境下,各国的金融市场飞速发展。但是相对于金融市场的迅速发展,相对的金融管制制度并不健全,导致在最近几十年间,国际金融市场中经常出现汇率、利率波动剧烈的情况。金融机构投资者迫切需要管理系统性风险。衍生金融工具在这个时机下应运而生。
1972年美国芝加哥商品交易所(CME)率先推出了货币期货合约,标志着世界上第一只衍生品的诞生。随后,美国堪萨斯期货交易所推出了价值线综合指数期货,标志着世界上第一只股指期货的诞生。随后的几十年间,在欧美国家的带动下,国际金融衍生品市场不断创新发展。1992年,韩国推出了KOSPI200股指期货,该期货合约是世界上交易量第二大的期货合约。香港期货交易所推出了香港恒生股指期货合约,该合约对于亚太地区有不可忽视的影响作用。
我国的证券市场近年来飞速发展,机构投资者不断涌入中国市场,ETF、保险公司、长期资本管理公司等机构投资者壮大了机构投资者的队伍。但是与国外相比,我国的金融市场发展还是很不成熟。我国二级市场上的系统风险远远高于欧美国家,涨停跌停的状况经常发生。机构投资者们迫切的需要衍生金融工具来规避系统性风险。在这种大环境下,股指期货的诞生符合广大投资者的需求,同时也契合时代需要,市场潜力巨大。
2010年4月,首批挂牌交易的四个沪深300股票指数合约推出,终结了我国金融市场上单边做多的局面,A股市场步入一个全新的做空时代。对于股指期货套期保值比率问题的研究,对恢复扭曲的市场价格、一直投机过度和增强市场流动性等方面具有重要的理论价值,并对机构投资者实现低风险利率具有现实意义,所以本文选择股指期货来进行套期保值的实证研究。
本文采用了2014年5月到11月的沪深300股指期货和现货的日真实交易数据,突破了以前常使用的仿真交易数据方法,以风险最小化套保思想为理论基础,运用OLS、双变量自回归、ECM、GARCH模型进行套保比率估计和套期保值绩效比较。为投资者能够合理的利用沪深300股指期货对冲风险,进行套期保值规避系统性风险提供理论性指导建议,使得我国的金融市场更加有效。
数据描述性统计分析
本文选取了沪深300股票指数和沪深300股指期货的日交易数据进行期货套期保值实证分析。St表示沪深300股票指数的收盘价,Ft表示沪深300股指期货的收盘价。本文对他们的收盘价取对数,得到他们价格的相对变化率,即lnSt、lnFt。因为最终的目的是让收益率之差波动最小,所以需要差分处理,即:
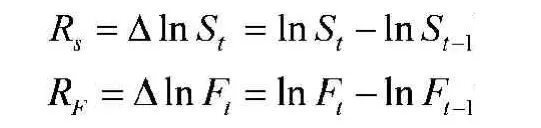
根据RS、RF,可以得到沪深300股票指数收益率的峰度为3.9288,同时偏度为-0.4248,JB统计量为3.0367;沪深300股指期货收益率的峰度为3.6883,偏度为-0.5459,JB统计量为3.1929;期货收益率和现货收益率的相关系数为0.9732。说明了期货收益率和现货收益率都不太符合正态分布,呈现尖峰厚尾的现象,期货和现货之间存在高度相关。
为防止“伪回归”,首先对沪深300股指期货(Ft)、沪深300股票指数(St)的对数收盘价序列和收益率序列进行ADF单位根检验,以检验变量的水平值和差分项是否为平稳序列,并确定其单整阶数。
从检验结果中可以看出,沪深300股指期货与沪深300股票指数对数收盘价ADF检验值均大于1%、5%和10%显著性水平的临界值,所以沪深300股指期货与沪深300股票指数对数收盘价序列存在单位根。而沪深300股指期货与鹏华沪深300ETF对数收盘价的一阶差分序列的ADF检验值均小于1%、5%和10%显著性水平的临界值,所以沪深300股指期货与沪深300股票指数对 数收盘价的一阶差分序列是平稳序列,从而沪深300股指期货与沪深300股票指数对数收盘价均是一阶单整序列。
经过ADF单位根检验,得到沪深300股指期货与沪深300股票指数对数收盘价均是一阶单整序列。下面进行协整性检验,采用EG两步法:首先,用 OLS 方法对 Lns和 Lnf进行协整回归或静态回归。其次,对残差(et)进行ADF检验,由于残差序列的均值为0,所以选择无截距项、无趋势项的检验。

表1 残差序列ARCH—LM检验结果
由Eviews输出结果有:在5%的显著性水平下,残差序列的t检验统计量达到了-2.5444,小于相应临界值,从而认为残差序列不存在单位根,是平稳序列,说明沪深300股指期货与沪深300股票指数对数收盘价之间存在协整关系,二者之间具有长期均衡关系。
最佳套保比率估计和套保绩效分析
(一)OLS套期保值模型计算
根据通过最小二乘法(OLS)对计算最优套保比率估计方法,建立如下的模型:
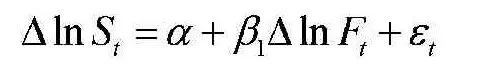
其中,斜率系数β1的估计值给出了套期保值比率的值。
用Eviews得出估计结果:
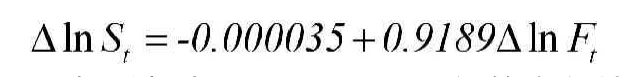
回归系数为0.9189,即最优的套保比率,而且在1%的显著性水平下是显著的。
(二)B-VAR套期保值模型计算
运用AIC原则对序列lnSt、lnFt的ADF多次检验,发现双变量向量自回归模型的滞后阶数为2时AIC、SC统计量最小,于是选用沪深300股指期货与鹏华沪深300ETF收益率建立B-VAR(2)模型:

用Eviews进行OLS估计,得到估计式:

从中可以看出h=0.923202
(三)ECM套期保值模型计算
误差修正模型(ECM)可以消除残差项的序列相关性和增加模型的信息量,误差修正项表示了现货价格和期货价格之间长期均衡偏差的影响。同时考虑期货和现货的VECM模型可表示为:
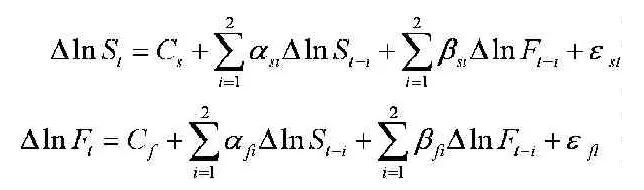
建立二阶滞后VECM模型,估计结果如下:
建立模型:

表2 不同模型套期保值绩效比较
(四)GARCH套期保值模型计算
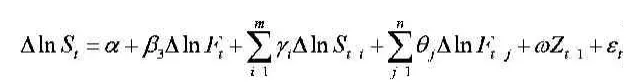
用EViwes进行OLS估计,得到估计式:
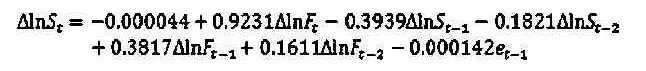
根据最佳套期保值比率公式得出最佳套期保值比率为h=0.9231。
对最初得到的OLS估计进行ARCHLM检验,结果见表1,发现p值小于0.05,拒绝无异方差假设,说明原模型存在ARCH效应。
通过Eviews对GARCH(1,1)模型进行参数估计,得到GARCH模型:

从上述模型中可以看出最佳套期保值比率为0.9432。
为了检查单元 GARCH模型是否消除了残差序列的ARCH效应,进行ARCHLM检验,检验发现p值为0.581,数值大于0.05,接受原假设,说明已经成功消除了原来金融时间序列中的ARCH效用。
(五)股指期货套期保值绩效比较
根据上面定义套期保值绩效的指标:

HE指标反映了进行套期保值相对于不进行套期保值风险降低的程度。本文可以该指标综合五种模型对沪深 300 股指期货与沪深300股指现货进行套保得到的套期保值比率得出套期保值效果,见表2。
由表2的效果比较得出:利用四种模型计算的套期保值率差别很小,通过观察,其中运用GARCH(1,1)模型计算套期保值率 0.9432最高,运用OLS模型计算套期保值率0.9189最低。利用四种模型观察到的套期保值效果中运用GARCH(1,1)模型进行套期保值的效果0.903534最好,运用B-VAR模型进行套期保值的效果0.903506在四种模型中最低,四种模型观察到的套期保值效果相差也不大,说明不管是 OLS、VAR、ECM还是GARCH(1,1)模型,都能有效降低沪深300股指现货的系统性风险。
其中单元GARCH的套期保值绩效最好,说明了从近段时间来说,沪深300股指期货收益率和沪深300股指现货的收益率所具有的时间序列的波动聚集性(ARCH效应)对进行OLS估计的影响比较大。可能是受到最近房地产低迷市场刺激、沪港通等一系列重大政策变更的影响,使得最近的期货和现货市场受到重大利好消息的刺激,波动性比较大。
从四种套期保值模型的整体套保绩效来看,套保效果都超过了90%,说明沪深300股指现货的推出能够有力的规避现如今金融市场上的系统性风险,虽然沪深300股指期货推出时间不是很长,但是他的发展非常迅速,并且他的套保绩效也优于一般的股指期货合约,能够满足现如今机构投资者规避风险的愿望。
结论
本文得到以下基本结论:第一,BVAR套期保值模型、ECM模型、GARCH模型都能降低系统风险,对现货进行套期保值。第二,OLS与B-VAR模型比较,OLS模型的绩效指标更大,说明OLS模型比BVAR模型更好。第三,ECM与GARCH模型进行比较,GARCH模型的绩效指标更大,说明GARCH模型更好。第四,综合来说对于沪深300股指现货与沪深股指期货,GARCH模型优于其他验证的模型。说明金融时间序列的波动性在最近一段时间中对传统OLS估计的影响较大,可能是因为最近出台的房地产市场刺激政策、沪港通等重大政策变更对于股市的影响较大,使得最近股市价格波动比较剧烈。
综上所述,本文建议,投资者选取沪深股指期货进行套期保值时,可以用GARCH模型来降低系统风险。投资者进行套期保值,大大降低了金融市场上的风险,让市场更为活跃,实现企业资金的合理利用和投资者收益的稳定性。
1.高辉,赵进文.沪深300股指套期保值及投资组合实证研究[J].管理科学,2007(4)
2.佟孟华.沪深300股指期货动态套期保值比率模型估计及比较—基于修正的ECM-BGARCH(1,1)模型的实证研究[J].数量经济技术经济研究,2011(4)
3.贺鹏,杨招军.恒生指数和沪深300股指期货套期保值效果对比研究[J].投资研究,2012(4)
4.李路苗,梁朝晖.沪深300股指期货最优套期保值实证研究[J].华北金融,2010(1)
5.蔡亚冬.沪深300股指期货套期保值策略简单研究[J].现代商业,2011(7)
6.李桂荣,孔令伟.沪深300股指期货套期保值有效性的实证研究[J].金融理论与实践,2012(2)
