基于有参和无参分析的风电功率短期点预测值置信区间估计

江岳文，林小雨

(福州大学电气工程与自动化学院，福建福州 350116)

0 引言

随着风电规模的不断扩大，风电并网运行对电力系统的影响也越来越大，为了降低由于风电不确定性造成的负面影响，文献［1－4］提出了各种方法来提高风速预测的精度，使风速点预测值尽量与实际吻合．但是无论如何提高风速预测的精度，由于其本身的不规律性使得风速的预测与实际总存在一定的偏差［5］，统计运行人员难以根据预测风速作出合适的决策［6－8］．通过设置风电的波动区间，用概率来描述其风电波动特性，更有利于决策者分析未来可能存在的不确定性风险，做出更合理的决策，以降低风险程度，优化为了提高可靠性而付出的成本．文献［9］指出基于风电功率区间预测的机组组合决策优于基于点预测的机组组合结果．

目前，对风电场功率区间估计的方法概括起来主要有以下三个方面:直接预测法、参数计算法和非参数计算法．直接预测风电功率区间，如文献［5］考虑到风速点预测值有较难克服的瓶颈，利用集对分析理论用于风电场风速的区间预测，并指出该方法亦适用于风电功率的区间预测;文献［8］基于分位点回归模型，通过支持向量机自适应地选取回归函数，实现对未来时刻风电功率波动区间的分析;文献［9－11］利用神经网络进行风电功率非参数置信区间预测，直接通过预测求得风电置信区间;文献［12］根据风电预测功率误差经验分布模型形成风电功率预测误差的概率分布函数，并利用非参数的回归技术预测风电功率区间．参数计算法通过确定的点预测值与实际值进行比较，确定误差大小，利用误差的有参分布特性求得风电场功率波动的置信区间，如文献［13］先进行风速点预测，求出功率点预测值，设风电功率预测误差分布满足Beta分布，获得功率预测区间．非参数计算法则考虑难以用某一确定的分布衡量风速或预测误差特性，故采用非参数法描述其概率密度函数，以求得分布函数，获得风电功率置信区间估计，如文献［14］采用BP神经网络对风电功率进行确定性预测，并在实际误差概率分布基础上，采用非参数区间估计风电功率短期预测值的置信区间，该文先估算误差概率密度曲线，经折算成为功率概率密度曲线，从而求功率分布函数，得出置信度下的功率区间分布;文献［15］在风电功率点预测值得基础上采用非参数核密度估计方法计算风电场功率预测误差的概率密度，求得误差分布曲线，得到满足一定置信概率的风功率预测区间．

基于历史实测风速满足威布尔分布和正态分布两种有参分布，利用推导得到的风电场功率分布规律，探讨未来短期风电点预测功率与未来实际功率偏差的概率，求得基于有参分析的风电点预测功率波动置信区间．同时，也采用非参数法进行风电功率置信区间的估计．最后，分别对两组历史数据样本进行分析，根据历史样本数据的分布特性，利用有参和无参分析方法研究未来短期点预测的风电功率在一定置信水平下的波动区间．

1 基于参数的风电点预测功率置信区间估计

1．1 基于风速满足两参数威布尔分布的风电场功率概率分布

对大量实测数据的统计结果表明，较长时间内风速的随机分布近似服从 Weibull函数［16］，其概率密度函数和分布函数分别为:

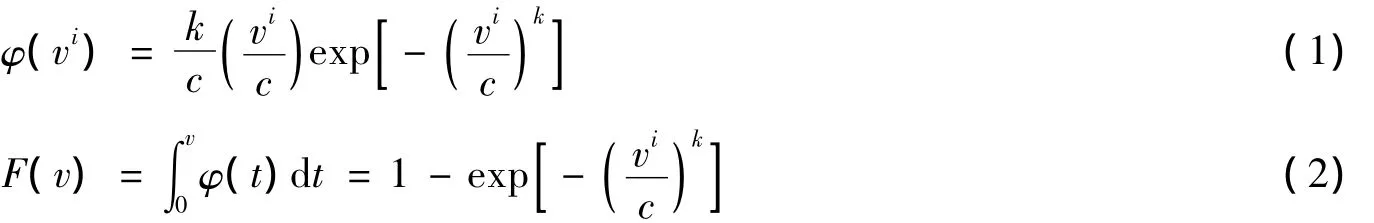
式中:k为形状系数;参数c为所描述地区的年平均风速，vi为风电场i的风速，单位是m·s－1．设风电场的出力可以用式(3)获得:

式中:PiW、PiWN、vi、viin、vir、viout分别表示风电场i的出力、额定出力、实际风速、切入风速、额定风速和切出风速．

根据文献［17］的推导可以得出风电场功率的分布为式(4)．

1．2 基于风速满足正态分布的风电场功率概率分布

1．2．1 风速的概率密度和概率分布

如果统计风速数据时间较短，利用正态分布来描述风速的概率分布可能更接近其真实分布函数，其概率密度函数为:

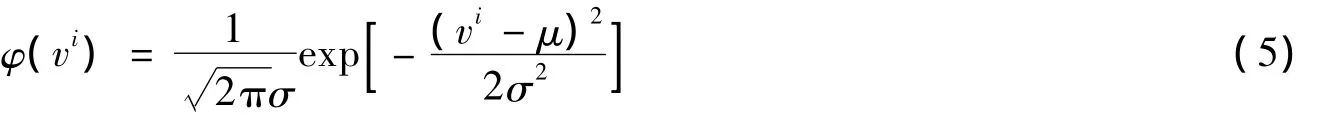
式中:u、σ分别为正态分布的平均值和标准差．

根据式(5)，得出风速正态分布的分布函数为:

式中:Φ()为标准正态分布函数．

1．2．2 风电场功率的概率密度和分布

根据式(3)和式(5)，则风电场功率分布的概率密度函数在风速为viin≤vi＜vir时的函数为:

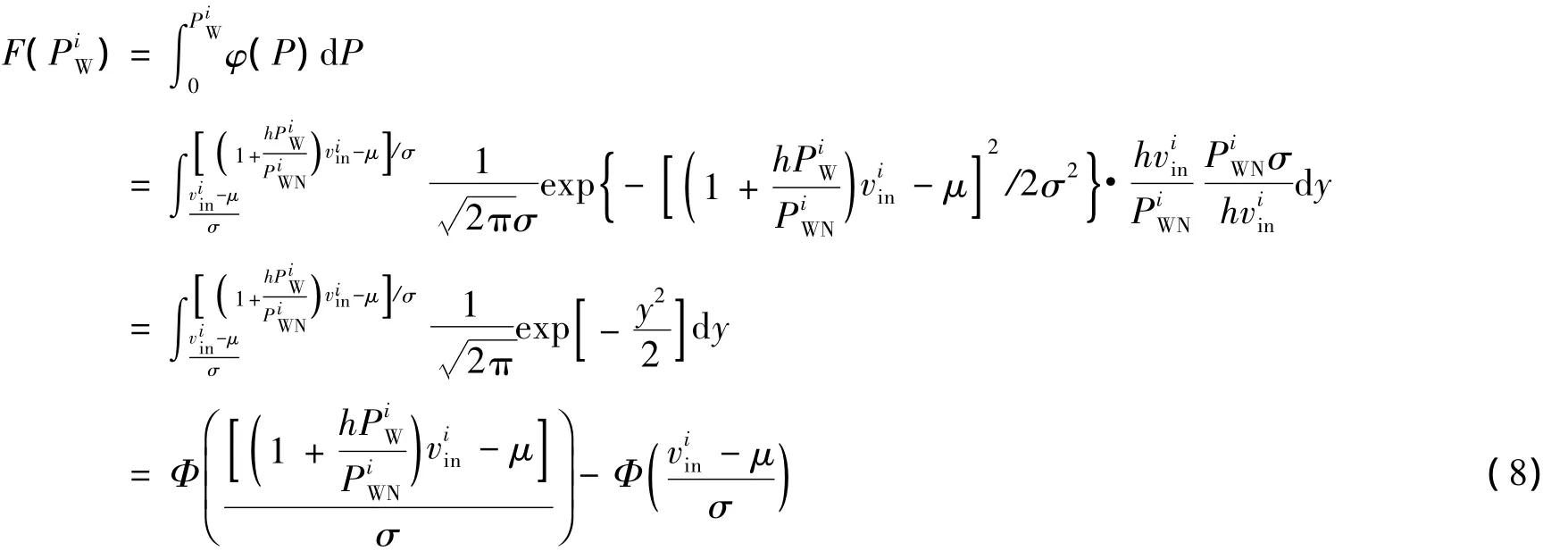
当风速在vi＜viin或vi＞viout，其功率的概率为:

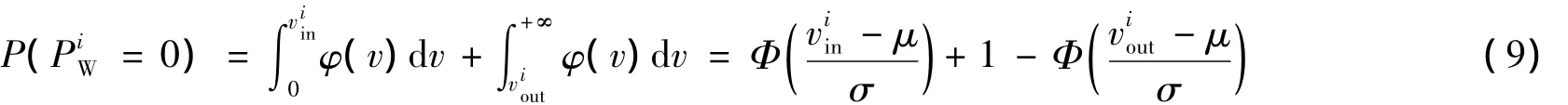
当风速在vir≤vi≤viout时，功率的概率为:

风电场功率小于0或大于额定功率的概率为:

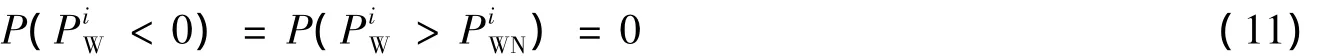
根据式(8)～(11)可以得出风速满足正态分布的风电场功率概率分布为:

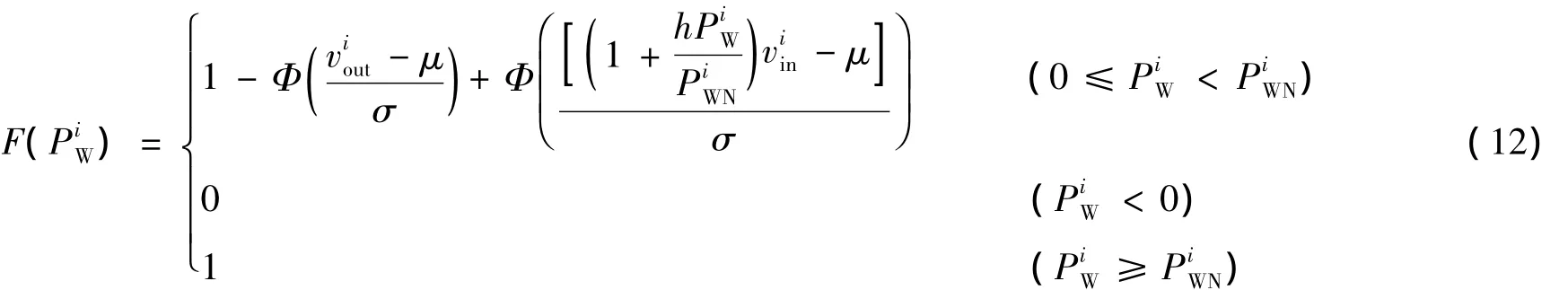
1．3 未来实际风电出力与预测风电出力偏差概率

1．3．1 风速满足威布尔分布的风电场功率偏差概率

设i风电场目前预测的功率为PiWf(0＜PiWf＜PiWN)，则i风电场未来实际风电出力PiWr大于、小于预测功率的概率分别为式(13)和式(14)．

同理，当PiWf=0或PiWf=PiWN，未来实际风电出力值与预测值偏差概率分别为式(15)和式(16)．

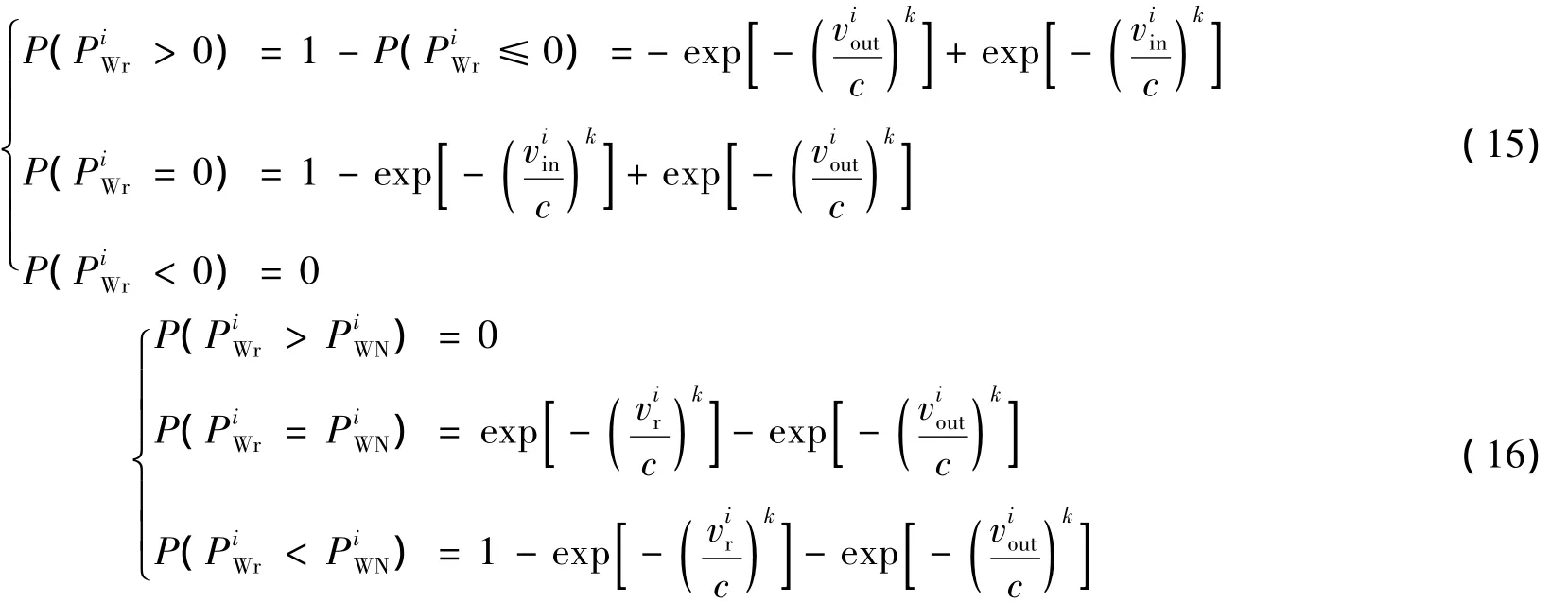
1．3．2 风速满足正态分布的风电场功率偏差概率

设i风电场目前预测的功率为PiWf(0＜PiWf＜PiWN)，则i风电场未来实际出力PiWr大于、等于、小于预测功率的概率为式(17)．

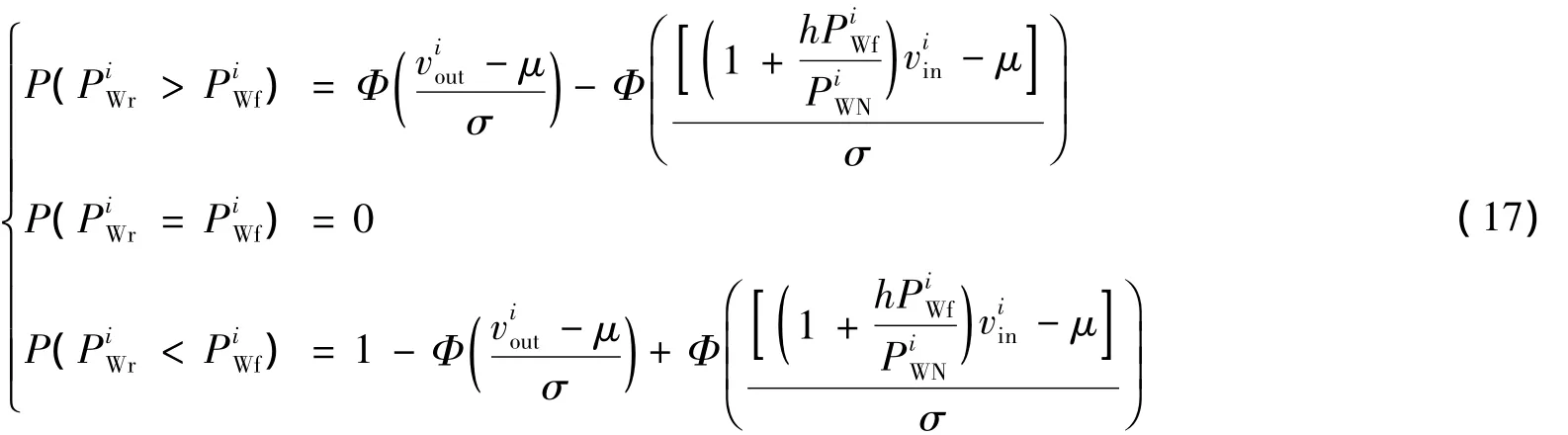
同理，当PiWf=0或PiWf=PiWN，未来实际风电出力值与预测值偏差概率分别为式(18)和式．(19)

1．4 风电场短期点预测值出力置信区间求取

1．4．1 非单侧置信区间的求取

当风电场短期点预测功率为0＜PiWf＜PiWN时，存在多个满足置信水平的区间．

假设置信区间功率下限值为PiWfd(0＜PiWfd≤PiWf)、功率上限值为PiWfu(PiWf≤PiWfu＜PiWN)，且PiWfd≤PiWf≤PiWfu．若 P(PiWfd≤PiWf≤PiWfu)=1－α，则根据置信区间的定义，可以得知区间［PiWfd，PiWfu］包含 PiWf的置信水平为1－α，则需要下式成立:

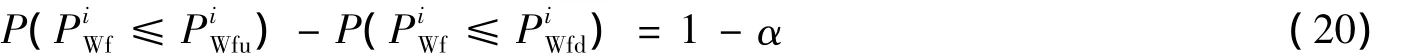
如果风速满足威布尔分布，式(20)可以表达成:

如果风速满足正态分布，则式(20)可以表达为:

由于在不同风电出力值上其上偏的概率和下偏的概率是不一样的，如果上偏的概率大于下偏的概率，则可以适当放大上偏的区间范围从而缩小下偏值，这样既保证能实现置信概率水平又能尽量缩小区间范围，有利于实际决策的正确性．即式(21)或式(22)的成立需满足约束条件(23)．

对于非单侧的满足置信水平的概率区间可能有多个，需取其中最小的一个跨度区间作为置信区间．

1．4．2 单侧置信区间的求取

当预测功率PiWf=PiWN或PiWf=0时，预测值置信区间求取就变成了单侧置信区间下限值或上限值的求取．

如果风电场风速满足威布尔分布，则单侧置信区间范围为［PiWfd，PiWN］或［0，PiWfu］，其中 PiWfd和PiWfu

由下式求出:

如果风速满足正态分布，同理，由式(25)求出Pi

Wfd和Pi

Wfu．

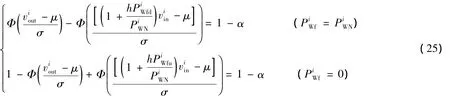
2 基于非参数的风电点预测功率置信区间估计

非参数估计是指在观察样本概率密度函数未知的前提下，通过核函数等方法对未知的概率密度函数进行估计．该方法通过数据本身的特性获得需要的信息，减少由于事先人为假定满足某种概率分布或概率密度函数所造成的概率误差．在文献［18］中，帕尔森教授首次利用核函数方法去模拟真实的概率密度函数，并指出如果采用合适的核函数和核窗口宽度，则利用核方法得出的概率密度可以无限接近样本真实的概率．

假设风电功率在某个时间段内的样本数据有n个，为P1，P2，…，Pn，在未知其概率密度函数的前提下，采用非参数的核密度函数估计法估计其概率密度．

在估计样本的概率密度上，用得最广泛的是高斯核函数，利用该核函数，可得核密度函数为:

式中:h为带宽系数，其它字母含义同上．

根据上述核密函数，得出风电场点预测功率PiWf的概率分布函数为:

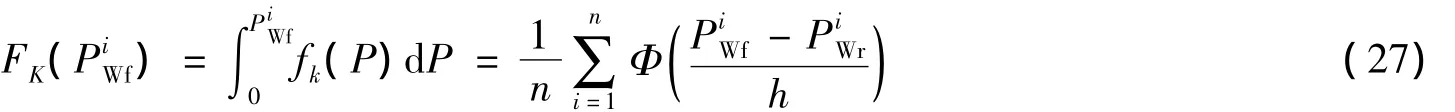
求某一置信区间，以1－α的置信度包含风电场的预测功率PiWf，假设区间为［PiWfd，PiWfu］，则需满足FK(PiWfu)－FK(PiWfd)=1－α．同样，满足这样置信水平的置信区间有多个，选取其中跨度最小的一个．

3 算例分析

福建某风电场共有50台永磁直驱式风力发电机组，每台机组额定容量为2 MW，切入风速3 m·s－1，额定风速15 m·s－1，切出风速为25 m·s－1，带宽系数h=2．

3．1 数据样本一

该风电场在2010年3月份风速数据基本满足威布尔分布，实际出力测点为每10 min 1个数据．图1显示该样本分布概率与两参数威布尔分布的概率较吻合．有少量风速较小的点和风速较大的测点与威布尔概率分布有一定的偏差．该数据样本中风速比较分散，起伏较大．预测数据为未来10 h风电场出力大小，测点间隔为5 min，预测出力曲线见图2．数据实测样本风况和预测风况有一定差距．根据威布尔分布的计算方法可以得出置信水平分别为0．9、0．8和0．7时的置信区间，见图2．

从图2可以看出，随着置信水平的增加，置信区间跨度也相应增加，在置信水平为0．9时，平均置信区间跨度为46．35 MW．由于时间跨度较大，风速数据比较分散，且3月份该地区的平均风速比较小，导致低出力概率比较大，因此无论是置信水平为0．7、0．8或0．9，其区间下界值都比较小，二者基本重合．如果下包络线上浮，将无法满足置信水平的要求．

从图3的未来实际出力与预测出力偏差概率分布可以看出测点上偏或下偏的可能性都比较大，因此置信区间的上下界都比较少与预测曲线重合．

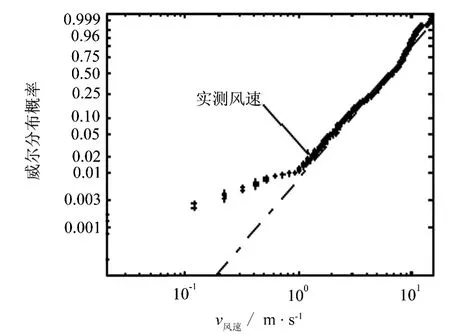
图1 风速分布与威布尔概率分布比较Fig．1 Comparison between factual wind speed distribution and Weibull distribution

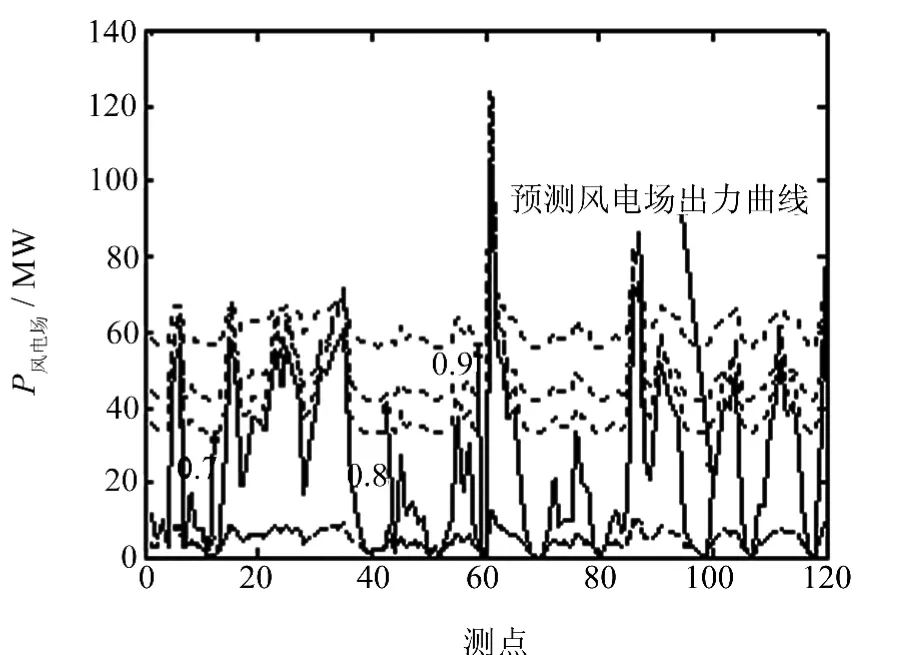
图2 预测风速在威布尔分布下的功率置信区间Fig．2 Confidence interval of forecast wind power for Weibull distribution of wind speed

图3 预测风速在威布尔分布下的功率偏差概率Fig．3 Deviation probability of forecast wind power for Weibull distribution of wind speed

图4 预测风速在威布尔分布下的非参数功率置信区间Fig．4 Confidence interval of forecast wind power for Weibull distribution of wind speed by nonparametric calculation

和图2同样的预测数据，利用非参数法估计风电点预测功率置信区间如图4．图2和图4的置信区间规律基本一致．在置信水平为0．9时，非参数法估计风电点预测功率置信区间平均跨度为39．75MW，比利用参数法略有缩小．

3．2 数据样本二

该组数据为2010年3月1日3:00:00～3:59:59实测风速数据，数据时间间隔为1 s，共3 600个数据．把该组数据的分布规律与正态分布比较，如图5所示．不难发现该组数据的分布特性比较适合正态分布规律．

预测数据为未来1 h风电场出力数据，测点间隔为30 s，预测曲线见图6．由正态分布计算方法得到预测功率的波动置信区间如图6，置信水平分别为0．8和0．9．非参数计算预测功率置信区间如图7所示．

由于数据实测样本风况和预测风况差不多，因此无论是利用参数或非参进行置信区间估计，其区间跨度都比较小．同样是0．9的置信水平，利用参数法进行预测功率置信区间估计平均跨度为7．43 MW，利用非参数法估计的置信区间跨度为7．85 MW．

从图6可以看出，其区间下界值有较多与功率预测值重合，很大的原因是风电场功率水平较低，其上偏的概率远大于下偏的概率．各测点上偏概率见图8，上偏概率基本都大于0．7，有的甚至接近1，故下界值都比较接近实际预测风电场出力值，这样能在置信水平满足要求的前提下尽量缩短置信区间．

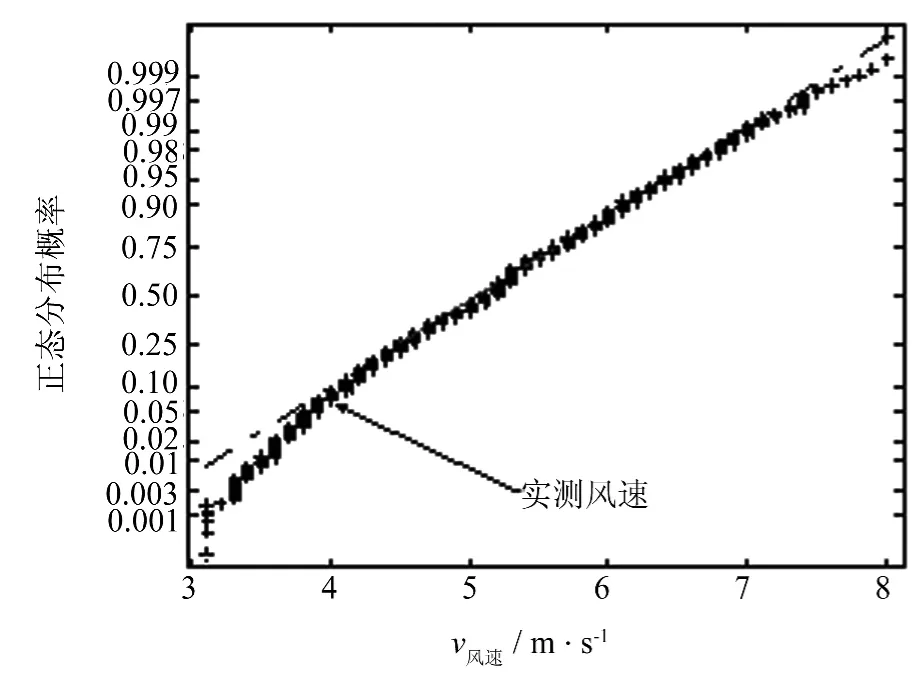
图5 实测风电场风速分布与正态概率分布比较Fig．5 Comparison between factual wind speed distribution in wind farm and normal distribution

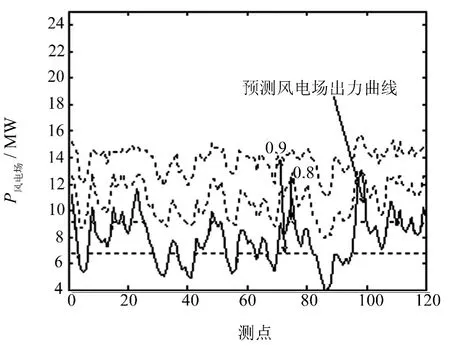
图6 预测风速在正态分布下的功率置信区间Fig．6 Confidence interval of forecast wind power for normal distribution of wind speed

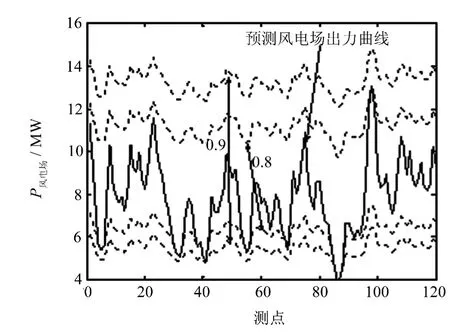
图7 预测风速在正态分布下的非参数功率置信区间Fig．8 Confidence interval of forecast wind power for normal distribution of wind speed by nonparametric calculation

图8 预测风速在正态分布下的功率偏差概率Fig．7 Deviation probability of forecast wind power for normal distribution of wind speed

4 结论

1)详细推导了基于有参分析的短期风电功率预测值置信区间的求取公式;

2)有参和无参计算均能进行风电功率预测值的置信区间估计，而且二者规律基本一致;

3)利用风况接近的实测数据样本进行有参或无参分析，对接下来进行风电功率短期预测数据的区间估计较为有利，既能保证置信水平的要求又能缩小置信区间的范围，提高其在电力系统应用和参考的价值．因此，在实际生产中可以从历史风速数据中选择与预测风况较接近的时段数据作为分析样本;

4)如果风电预测功率上偏的概率比较大时，满足置信水平的风电场功率最小置信区间下界基本都接近或等于风电场出力预测值;

5)有参和无参区间估计方法能为评估风电的间歇性和波动性提供一种有效评价方法，并获得相应概率指标;能为含风电的电力系统规划、调度、运行、可靠性分析、风险评估等方面提供参考依据．