一类两种群浮游生物相克模型平衡点稳定性分析

林玉花，陈婉琳，王海娜，张惠英

(1．福州大学数学与计算机科学学院，福建福州 350116;2．厦门市大同中学，福建厦门 361008)

0 引言

浮游植物是海洋环境中的初级生产者，在海洋生态系统的能量传递与物质循环中起重要作用，在海洋生物资源和生态系统中占有重要地位［1］．由于人类将大量工业废水、生活污水等植物营养物质排入湖泊、河口等，导致水域环境的富营养化，赤潮与水华成为当今社会迫切需要解决的一个极为严峻的生态环境与社会经济问题［2］，研究表明，在海洋中相对其他浮游藻类，有害藻类取得生长优势的主要原因之一可能是浮游植物的植化相克作用，所以植化相克作用对赤潮与水华的形成具有重要作用．近年来，生物治理方法越来越受到人们的关注，它主要是利用生物间的竞争、抑制和捕食的关系，在赤潮区引入无害藻类以抑制赤潮藻的繁殖，从而减少赤潮的发生［3］．因此对浮游植物相克模型进行研究具有很大的现实意义，学者们对具有相克作用的浮游植物模型的动力学行为展开了系列研究，以期可以为赤潮与水华的发生提供一些早期预警信息［4－7］．Bandyopadhyay［5］提出并研究了如下两种群浮游生物相克模型:

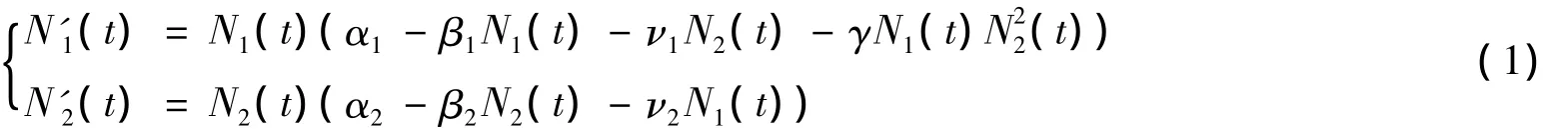
其中:N1(t)，N2(t)分别代表两个相互竞争的浮游生物种群在t时刻的种群密度;αi，i=1，2表示两种群的内凛增长率;βi，i=1，2表示两种群的种内竞争率;νi，i=1，2表示两种群的种间竞争率;γN1(t)N22(t)表示两种群个体相遇时，N2种群释放的毒素对N1种群的影响．对于该模型，文［5］探讨了边界平衡点局部渐近稳定性和内部平衡点的全局吸引性．最近，在文［7］中指出文［5］的证明是不严密的，其主要结果是否成立还有待进一步的研究，文［7］已经针对非自治情形探讨了系统的全局吸引性问题，得到了系统正解全局渐近稳定的充分性条件，补充和完善了文［5］的结果．针对文［5］，尚有如下问题有待研究:系统的边界平衡点是否可能全局渐近稳定，毒素对系统边界平衡点的稳定性影响如何;能否在文［5］的工作基础上，通过克服文［5］分析上的错误之处，给出一组合理的保证系统正平衡点全局吸引的充分性条件呢?本文旨在对这两个问题给出肯定回答．

由生态学含义知道，系统(1)中的所有系数均为大于零的常数，且系统(1)的初值满足N1(0)＞0，N2(0)＞0．易知，对∀t≥0，系统的任意解N1(t)＞0，N2(t)＞0．

1 主要结果及其证明

完全类似于文［7］引理2．2及定理2．1的证明，有定理1 若条件

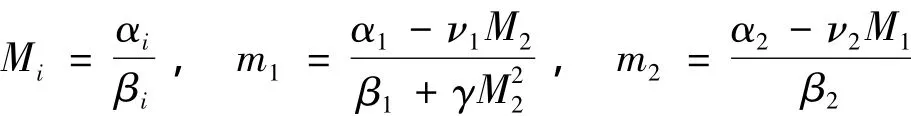
由文［5］可知系统(1)有三个边界平衡点 E00(0，0)，E10(α1·β1－1，0)，E01(0，α2·β2－1);同时若条件N2*＜α2·β2－1，α1ν2－β1α2＜0成立，则系统(1)至少有一个正平衡点．且其中N2*满足下面方程

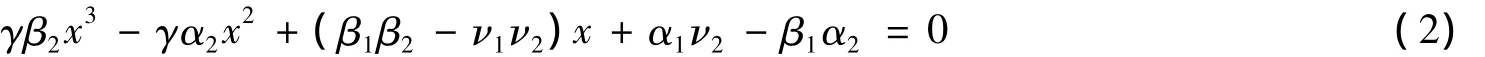
下面给出系统(1)存在唯一正平衡点的一个充分性条件．

定理2 若条件

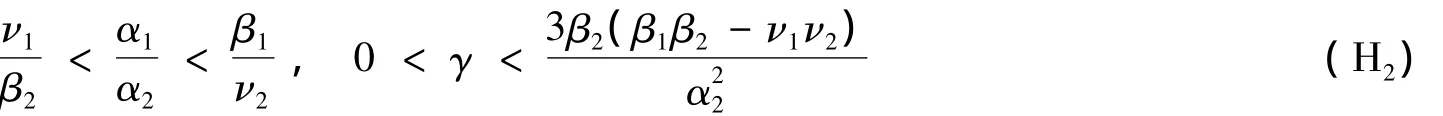
成立，则系统(1)存在唯一的正平衡点E*(N*1，N*2)．

证明 令

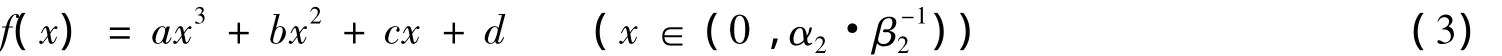
其中:a= γβ2，b= － γα2，c= β1β2－ ν1ν2，d= α1ν2－ β1α2．由于 N*2＜ α2·β－12是满足方程 f(x)=0 的一个根，因此要证得系统(1)只有一个正平衡点只需证明方程f(x)=0在x∈(0，α2·β－12)的内只有一个正根．由条件(H2)的第一个条件，有c＞0，d＜0．注意到:f'(x)=3ax2+2bx+c，由条件(H2)有:Δ =4b2－12ac=4γ2α22－12γβ2c ＜ 0．这表明，当x∈(0，α2·β－12)，f'(x)＞ 0即f(x)在(0，α2·β－12)单调增加．注意到f(0)=d＜0，由条件(H2)的第二个条件

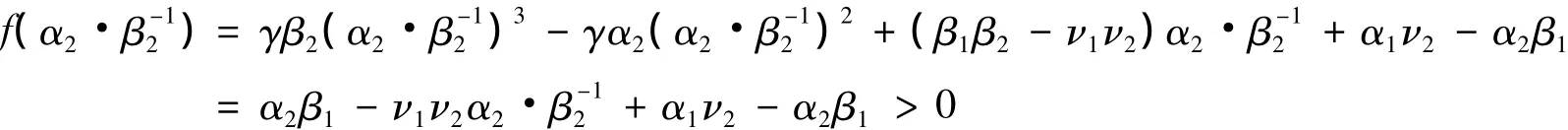
可知f(x)在(0，α2·β－12)上有且仅有一个根，因此N*2存在且唯一，即系统(1)存在唯一的正平衡点．定理证毕．

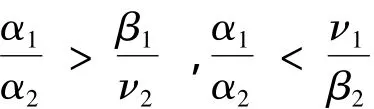
定理3 若E10局部渐近稳定，此外，进一步假设条件

成立，则E10全局渐近稳定．

证明 令 N10= α1·β－11，则 α1= β1N10，E10=(N10，0)．构造 Lyapunov函数

注意到，对所有的(N1，N2)∈(［0，+∞)，［0，+∞))，且(N1，N2)≠(N10，0)有V1(N1，N2)＞0，V1(N10，0)=0．沿着系统(1)的正解计算V1(N1，N2)关于t的导数，

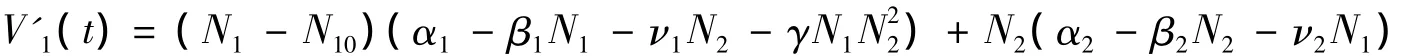
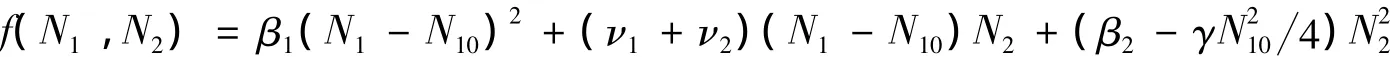
则

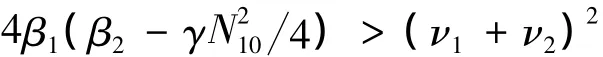
于是f(N1，N2)＞0．从而有:

所以E10全局渐近稳定．

定理4 若E01局部渐近稳定，此外，进一步假设条件:

成立，则E01全局渐近稳定．

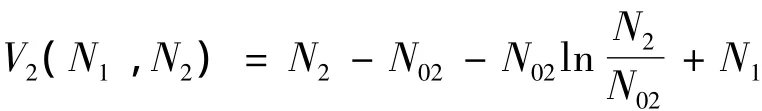
注意到，对所有的(N1，N2)∈(［0，+∞)，［0，+∞))，且(N1，N2)≠ (0，N02)有 V2(N1，N2)＞0，V2(0，N02)=0．沿着系统(1)的正解计算V2(N1，N2)关于t的导数，

因此α －νN＜0．令:

1102

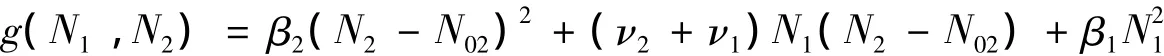
则

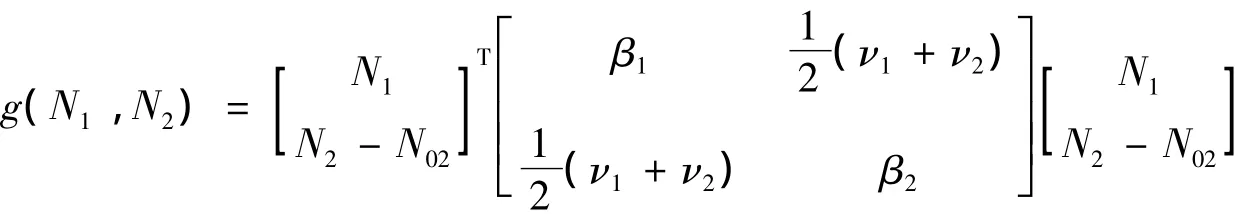
由条件(H4)可知，g(N1，N2)＞0．从而有

所以E01全局渐近稳定．

定理5 假设条件(H1)成立，此外，进一步假设

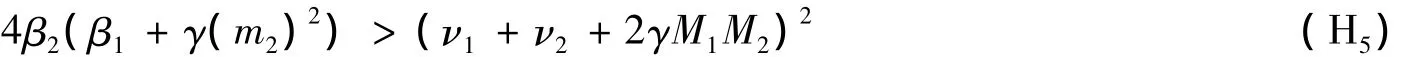
成立，其中m2，M1，M2是定理1中所定义的，则E*(N1*，N2*)全局渐近稳定．

证明 由条件(H5)知存在足够小的ε＞0使得

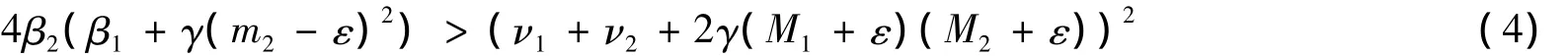
由条件(H1)成立，可知定理1成立，对上述ε＞0，存在足够大的T，t＞T时有

成立，从而由(4)知当t＞T时不等式

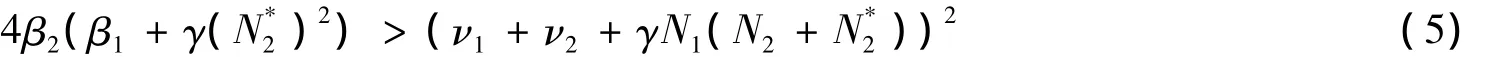
成立．今构造Lyapunov函数

由文［5］可知:V'(t)=－XTAX，其中:

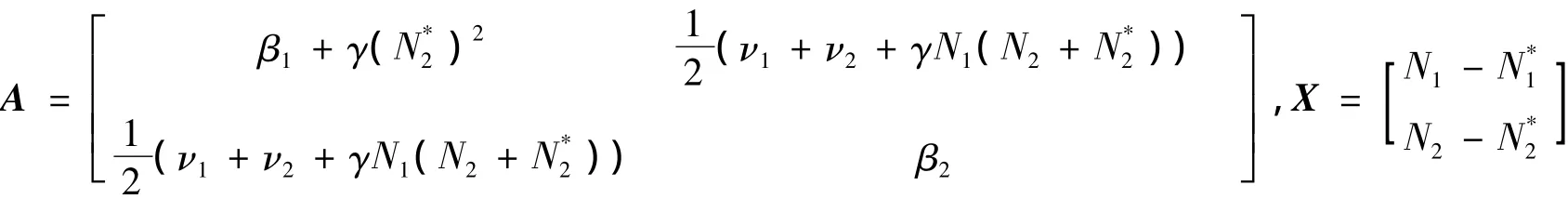
由式(5)知t＞T时A正定，从而V'(t)≤0．当且仅当N1=N*1，N2=N*2时取等号，这表明正平衡点是全局吸引的，定理证毕．

注1 文［7］给出系统(1)的正平衡点E*(N*1，N*2)全局渐近稳定的充分性条件使系统(1)持久和条件

成立．本文定理5也是在系统(1)满足持久性条件下，考虑正平衡点的稳定性问题．条件(H5)，(H6)都使系统的系数满足一定的不等式，但是这两个条件的表达式不一样，所给的范围也是不一样的，后面将给出例子来说明这一点．

2 数值模拟

例1

相应于系统(1)，有 α1=1．5，α2=0．8，β1=0．1，β2=0．2，ν1=0．02，ν2=0．06，γ =0．002．由Maple软件计算可知，系统(6)有边界平衡点E10=(15，0)，E01=(0，4)，不存在正平衡点且

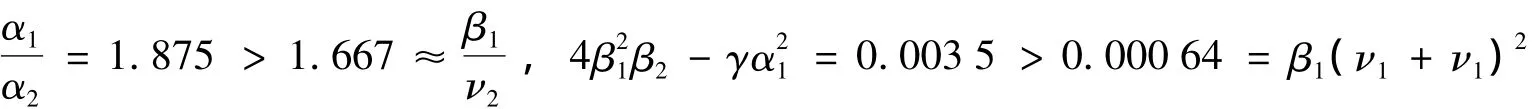
这表明系统(6)满足定理3的条件，从而E10全局渐近稳定，图1(a)是它的数值模拟图，所有满足不同初值的解最后都趋于点E10．

例2

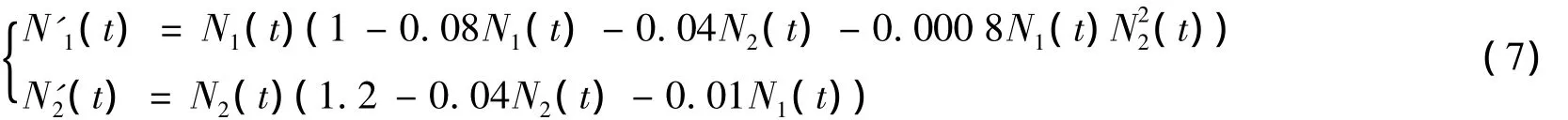
相应于系统(1)，有 α1=1，α2=1．2，β1=0．08，β2=0．04，ν1=0．04，ν2=0．01，γ =0．000 8．由Maple软件计算可知，系统(6)有边界平衡点E10=(12．5，0)，E01=(0，30)，不存在正平衡点且

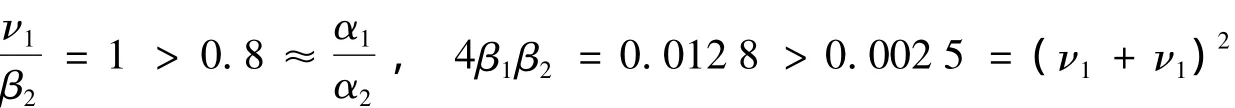
因此系统(6)满足定理4的条件，从而E01全局渐近稳定，图1(b)是它的数值模拟图，所有满足不同初值的解最后都趋于点E01．

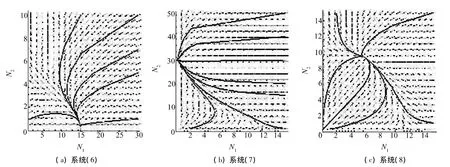
图1 系统(6)，(7)，(8)的模值摸拟图Fig．1 Simulation diagrams of system(6)，(7)and(8)

例3

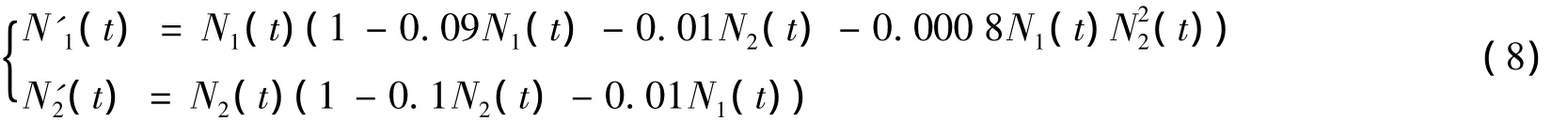
相应于系统(1)，有 α1=1，α2=1，β1=0．09，β2=0．1，ν1=0．01，ν2=0．01，γ =0．000 8．由Maple软件计算可知，系统(7)有边界平衡点E10=(11．1，0)，E01=(0，10)和唯一的正平衡点E*(N*1，N*2)=(5．615 618 707，9．438 438 129)，且 M1≈11，M2=10，m2≈8．9，从而:

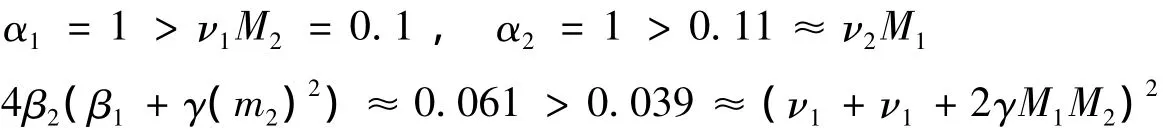
此外，有 β1=0．09= ν2+ γM22=0．09，β2=0．1 ＜ 0．19 ≈ ν1+2γM1M2．

因此，系统(8)满足定理1和5的条件，但条件(H6)不成立．图1(c)是它的模拟图，该模拟图表明，系统(8)当系统满足条件(H5)但不满足条件(H6)时，仍然全局渐近稳定．

3 结语

在文［5］的基础上，通过构造适当的Lyapunov函数得到保证系统(1)的边界平衡点全局渐近稳定的充分性条件，注意到保证E10全局稳定的条件跟表示毒素的系数γ有关，而保证E01稳定的条件跟毒素无关，但是由于这仅是充分性条件，而不是充要条件，目前还无法断言E01的稳定性跟毒素无关，这是一个有趣的有待进一步探索的问题．此外，得到了正平衡点E*(N*1，N*2)全局渐近稳定的一组充分性条件，有效补充和完善了文［5］的工作．